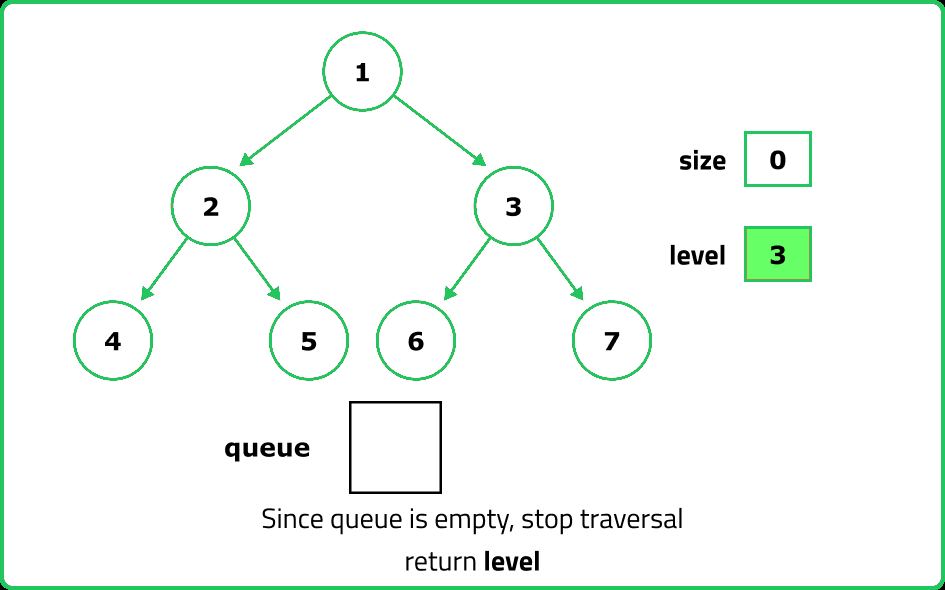
Maximum Depth in BT
Binary Trees
Medium Problems
Medium
Given root of the binary tree, return its maximum depth.
A binary tree's maximum depth is number of nodes along the longest path from from root node down to the farthest node.
Examples:
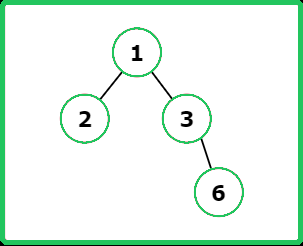
Input : root = [1, 2, 3, null, null, null , 6]
Output : 3
Explanation : The path from root node 1 to node with value 6 has maximum depth with 3 nodes along path.
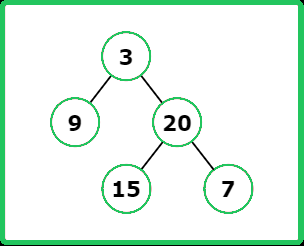
Input : root = [3, 9, 20, null, null, 15 , 7]
Output : 3
Explanation : The path from root node 3 to node with value 15 has maximum depth with 3 nodes along path.
There exists other paths to reach the solution.
Input : root = [5, 1, 2, 8, null, null, 5, null, 4, null, null, 7]
Constraints
- 1 <= Number of Nodes <= 104
- 0 <= Node.val <= 104
Hints
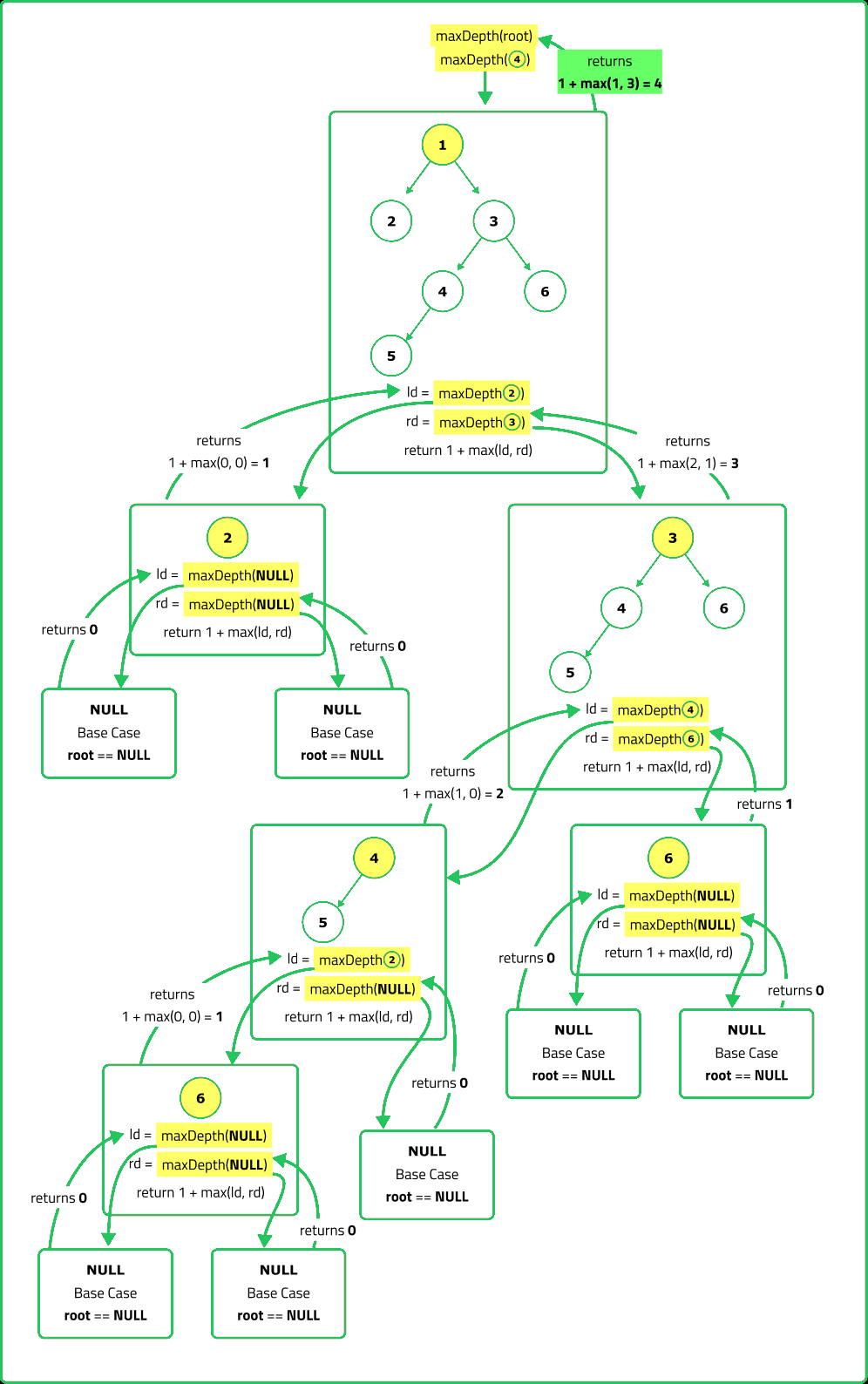
- Since the depth of a node is determined by its deepest child, we can use a divide-and-conquer approach: the depth of a node is 1 + max(depth of left subtree, depth of right subtree). This naturally fits a recursive Depth-First Search (DFS) strategy.
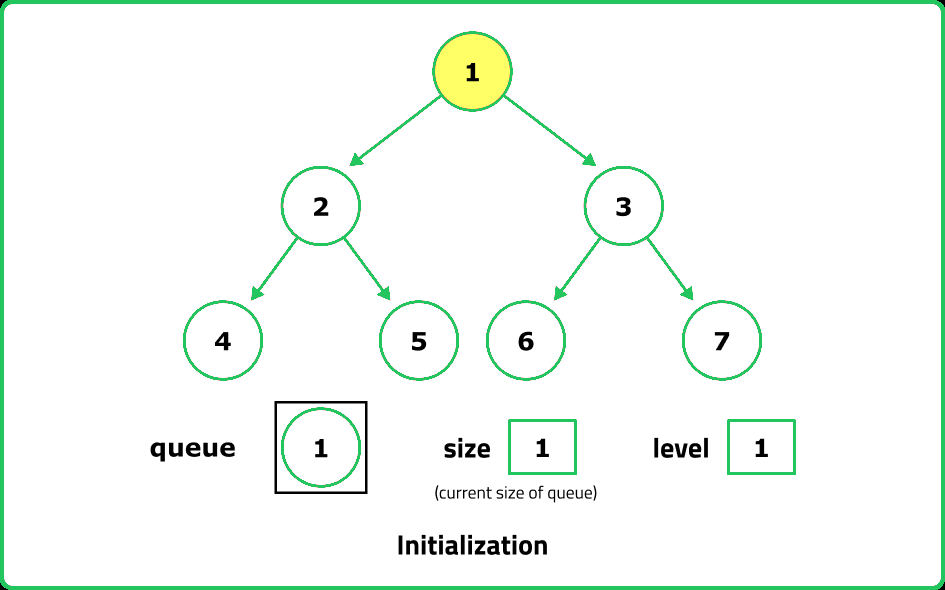
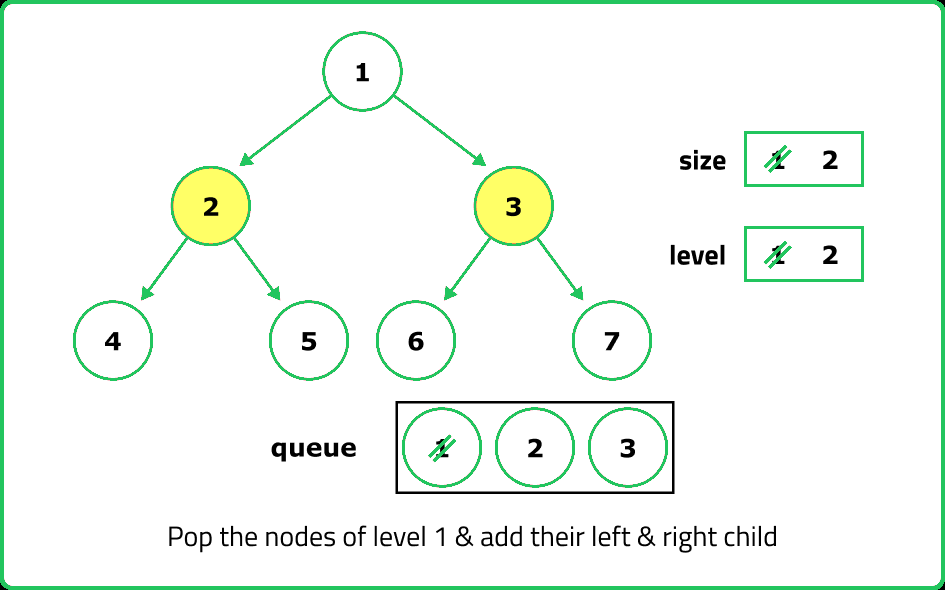
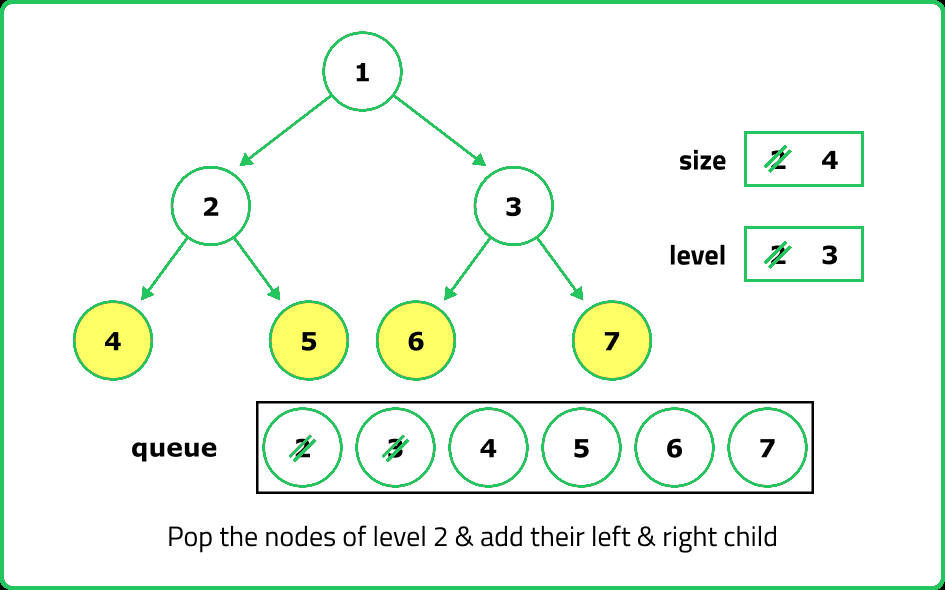
- An iterative approach can be used with Breadth-First Search (BFS). By using a queue, we traverse each level of the tree, counting the number of levels until we reach the last node. BFS is particularly useful for large trees since it avoids deep recursion stack issues.
Company Tags
Zoho
Mastercard
Wayfair
Freshworks
Electronic Arts
Qualcomm
Target
Bungie
Bain & Company
Zynga
Nutanix
Broadcom
GE Healthcare
Teladoc Health
Cerner
Etsy
HCL Technologies
Red Hat
NVIDIA
Flipkart
DoorDash
OYO Rooms
McKinsey & Company
ARM
Stripe
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe