Boundary Traversal

Intuition

The boundary traversal algorithm aims to traverse the boundary of a binary tree in an anti-clockwise direction. The traversal is divided into three main parts: the left boundary, the bottom boundary (leaf nodes), and the right boundary. The left boundary traversal starts from the root and moves to the leftmost child, switching to the right child if the left is unavailable, until reaching a leaf node. The bottom boundary includes all leaf nodes using a simple preorder traversal. The right boundary traversal is similar to the left boundary but in the reverse direction, moving from the root to the rightmost child, and reversing the order of nodes in the result.

Approach

Begin by initializing an empty array to collect the nodes encountered during the boundary traversal. Additionally, create a helper function designed to determine whether a node is a leaf, which helps to prevent the inclusion of duplicate nodes in the traversal.
Define a recursive function called addLeftBoundary and use a vector to keep track of nodes on the left boundary. Start this function at the root of the tree and proceed down the leftmost path until you reach a leaf node. For every non-leaf node encountered, append its value to the result list. Continue by traversing to the left child, and if the left child is not available, call the function on the right child.

Next, create a recursive function named addLeafNodes and use a vector to store the nodes found at the bottom of the tree. When this function encounters a leaf node, add its value to the result list. Recursively visit the left and right subtrees of the current node following a preorder traversal pattern.

Define another recursive function, addRightBoundary, and use a vector to capture nodes on the right boundary. Begin at the root and traverse the rightmost path of the tree until reaching a leaf node. For each non-leaf node, first attempt to traverse to its right child; if that child is unavailable, move to the left child. As the recursion returns, add the current node's value to the result list.

Solution

#include <bits/stdc++.h>
using namespace std;

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int data;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
 * };
 **/

class Solution {
public:
    // Function to check if a node is a leaf
    bool isLeaf(TreeNode* root) {
        return !root->left && !root->right;
    }

    // Function to add the left boundary of the tree
    void addLeftBoundary(TreeNode* root, vector<int>& res) {
        TreeNode* curr = root->left;
        while (curr) {
            if (!isLeaf(curr)) {
                res.push_back(curr->data);
            }
            if (curr->left) {
                curr = curr->left;
            } else {
                curr = curr->right;
            }
        }
    }

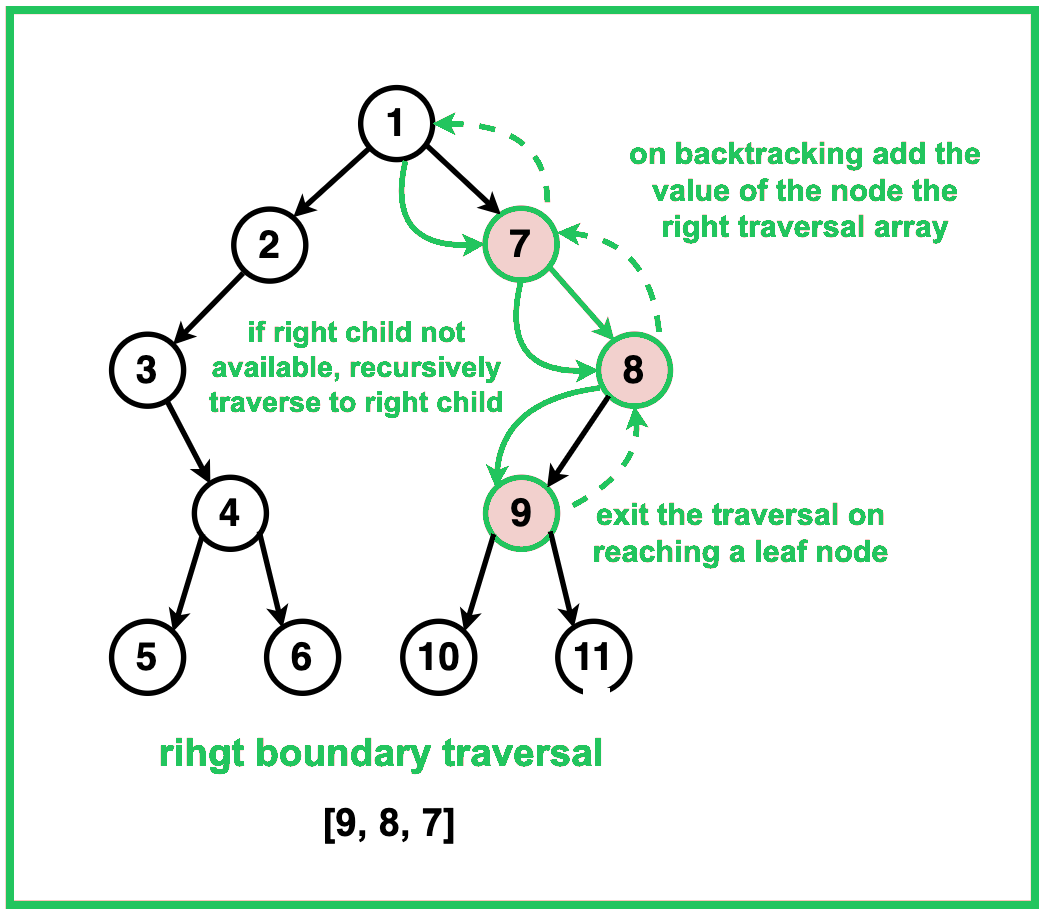
    // Function to add the right boundary of the tree
    void addRightBoundary(TreeNode* root, vector<int>& res) {
        TreeNode* curr = root->right;
        vector<int> temp;
        while (curr) {
            if (!isLeaf(curr)) {
                temp.push_back(curr->data);
            }
            if (curr->right) {
                curr = curr->right;
            } else {
                curr = curr->left;
            }
        }
        for (int i = temp.size() - 1; i >= 0; --i) {
            res.push_back(temp[i]);
        }
    }

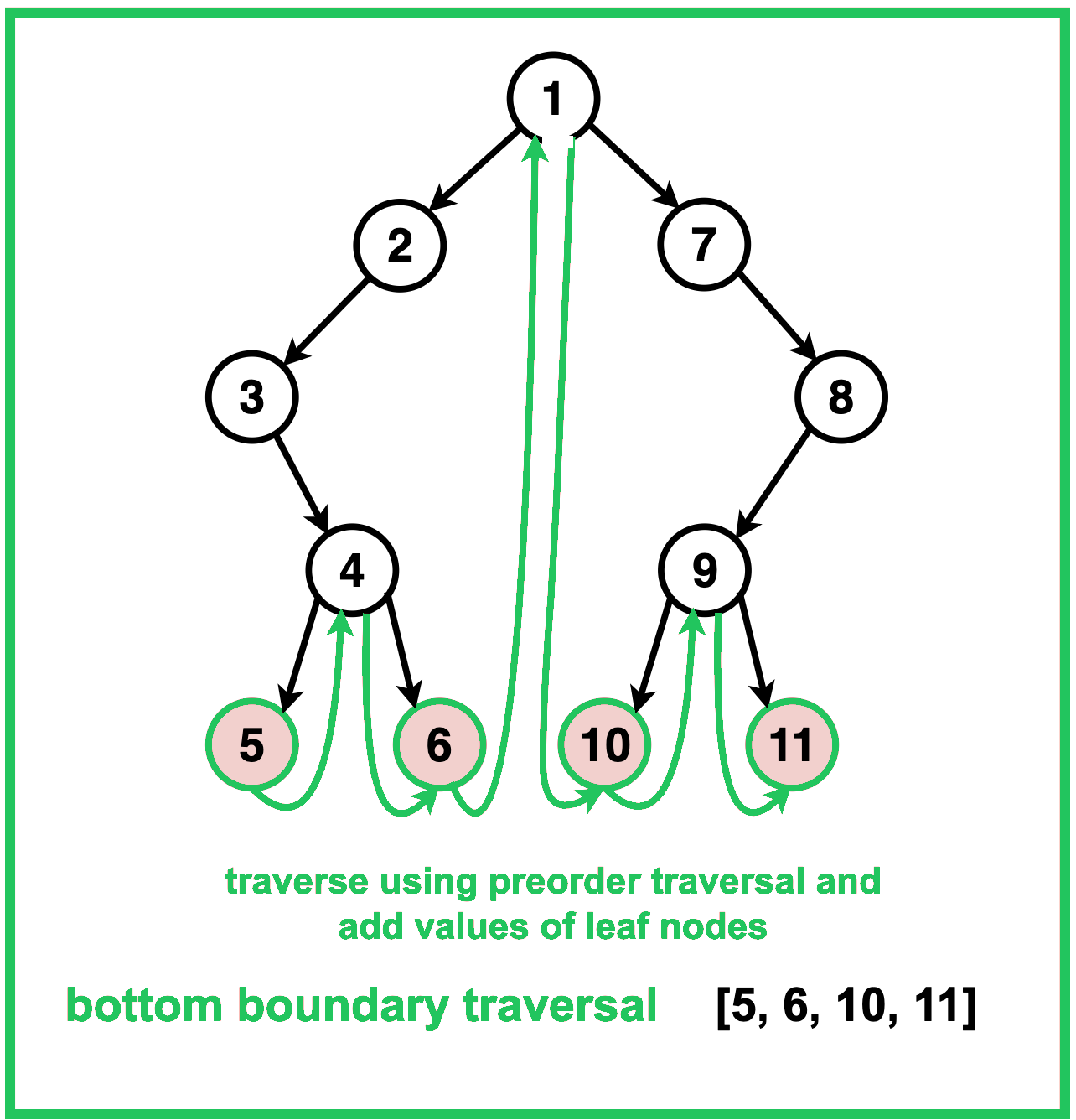
    // Function to add the leaves of the tree
    void addLeaves(TreeNode* root, vector<int>& res) {
        if (isLeaf(root)) {
            res.push_back(root->data);
            return;
        }
        if (root->left) {
            addLeaves(root->left, res);
        }
        if (root->right) {
            addLeaves(root->right, res);
        }
    }

    // Main function to perform the boundary traversal of the binary tree
    vector<int> boundary(TreeNode* root) {
        vector<int> res;
        if (!root) {
            return res;
        }
        if (!isLeaf(root)) {
            res.push_back(root->data);
        }

        addLeftBoundary(root, res);
        addLeaves(root, res);
        addRightBoundary(root, res);

        return res;
    }
};

// Helper function to print the result
void printResult(const vector<int>& result) {
    for (int val : result) {
        cout << val << " ";
    }
    cout << endl;
}

int main() {
    // Creating a sample binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->left = new TreeNode(6);
    root->right->right = new TreeNode(7);

    Solution solution;

    // Get the boundary traversal
    vector<int> result = solution.boundary(root);

    // Print the result
    cout << "Boundary Traversal: ";
    printResult(result);

    return 0;
}
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int data;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int val) { data = val; left = null, right = null; }
 * }
 **/

class Solution {
    // Function to check if a node is a leaf
    public boolean isLeaf(TreeNode root) {
        return root.left == null && root.right == null;
    }

    // Function to add the left boundary of the tree
    public void addLeftBoundary(TreeNode root, List<Integer> res) {
        TreeNode curr = root.left;
        while (curr != null) {
            if (!isLeaf(curr)) {
                res.add(curr.data);
            }
            if (curr.left != null) {
                curr = curr.left;
            } else {
                curr = curr.right;
            }
        }
    }

    // Function to add the right boundary of the tree
    public void addRightBoundary(TreeNode root, List<Integer> res) {
        TreeNode curr = root.right;
        List<Integer> temp = new ArrayList<>();
        while (curr != null) {
            if (!isLeaf(curr)) {
                temp.add(curr.data);
            }
            if (curr.right != null) {
                curr = curr.right;
            } else {
                curr = curr.left;
            }
        }
        for (int i = temp.size() - 1; i >= 0; --i) {
            res.add(temp.get(i));
        }
    }

    // Function to add the leaves of the tree
    public void addLeaves(TreeNode root, List<Integer> res) {
        if (isLeaf(root)) {
            res.add(root.data);
            return;
        }
        if (root.left != null) {
            addLeaves(root.left, res);
        }
        if (root.right != null) {
            addLeaves(root.right, res);
        }
    }

    // Main function to perform the boundary traversal of the binary tree
    public List<Integer> boundary(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        if (!isLeaf(root)) {
            res.add(root.data);
        }

        addLeftBoundary(root, res);
        addLeaves(root, res);
        addRightBoundary(root, res);

        return res;
    }

    // Helper function to print the result
    public static void printResult(List<Integer> result) {
        for (int val : result) {
            System.out.print(val + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        // Creating a sample binary tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);
        root.right.left = new TreeNode(6);
        root.right.right = new TreeNode(7);

        Solution solution = new Solution();

        // Get the boundary traversal
        List<Integer> result = solution.boundary(root);

        // Print the result
        System.out.print("Boundary Traversal: ");
        printResult(result);
    }
}
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.data = val
#         self.left = left
#         self.right = right

class Solution:
    # Function to check if a node is a leaf
    def isLeaf(self, root):
        return not root.left and not root.right

    # Function to add the left boundary of the tree
    def addLeftBoundary(self, root, res):
        curr = root.left
        while curr:
            if not self.isLeaf(curr):
                res.append(curr.data)
            if curr.left:
                curr = curr.left
            else:
                curr = curr.right

    # Function to add the right boundary of the tree
    def addRightBoundary(self, root, res):
        curr = root.right
        temp = []
        while curr:
            if not self.isLeaf(curr):
                temp.append(curr.data)
            if curr.right:
                curr = curr.right
            else:
                curr = curr.left
        res.extend(temp[::-1])

    # Function to add the leaves of the tree
    def addLeaves(self, root, res):
        if self.isLeaf(root):
            res.append(root.data)
            return
        if root.left:
            self.addLeaves(root.left, res)
        if root.right:
            self.addLeaves(root.right, res)

    # Main function to perform the boundary traversal of the binary tree
    def boundary(self, root):
        res = []
        if not root:
            return res
        if not self.isLeaf(root):
            res.append(root.data)

        self.addLeftBoundary(root, res)
        self.addLeaves(root, res)
        self.addRightBoundary(root, res)

        return res

# Helper function to print the result
def printResult(result):
    for val in result:
        print(val, end=" ")
    print()

# Creating a sample binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.right = TreeNode(7)

solution = Solution()

# Get the boundary traversal
result = solution.boundary(root)

# Print the result
print("Boundary Traversal: ", end="")
printResult(result)
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *      constructor(val = 0, left = null, right = null){
 *          this.data = val;
 *          this.left = left;
 *          this.right = right;
 *      }
 * }
 **/

class Solution {
    // Function to check if a node is a leaf
    isLeaf(root) {
        return !root.left && !root.right;
    }

    // Function to add the left boundary of the tree
    addLeftBoundary(root, res) {
        let curr = root.left;
        while (curr) {
            if (!this.isLeaf(curr)) {
                res.push(curr.data);
            }
            if (curr.left) {
                curr = curr.left;
            } else {
                curr = curr.right;
            }
        }
    }

    // Function to add the right boundary of the tree
    addRightBoundary(root, res) {
        let curr = root.right;
        const temp = [];
        while (curr) {
            if (!this.isLeaf(curr)) {
                temp.push(curr.data);
            }
            if (curr.right) {
                curr = curr.right;
            } else {
                curr = curr.left;
            }
        }
        for (let i = temp.length - 1; i >= 0; --i) {
            res.push(temp[i]);
        }
    }

    // Function to add the leaves of the tree
    addLeaves(root, res) {
        if (this.isLeaf(root)) {
            res.push(root.data);
            return;
        }
        if (root.left) {
            this.addLeaves(root.left, res);
        }
        if (root.right) {
            this.addLeaves(root.right, res);
        }
    }

    // Main function to perform the boundary traversal of the binary tree
    boundary(root) {
        const res = [];
        if (!root) {
            return res;
        }
        if (!this.isLeaf(root)) {
            res.push(root.data);
        }

        this.addLeftBoundary(root, res);
        this.addLeaves(root, res);
        this.addRightBoundary(root, res);

        return res;
    }
}

// Helper function to print the result
function printResult(result) {
    for (const val of result) {
        console.log(val);
    }
}

// Creating a sample binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);

const solution = new Solution();

// Get the boundary traversal
const result = solution.boundary(root);

// Print the result
console.log("Boundary Traversal: ");
printResult(result);

Complexity Analysis

Time Complexity: O(N) where N is the number of nodes in the Binary Tree. This is due to traversing the left boundary, bottom nodes, and right boundary sequentially, each operation being at most O(N).

Space Complexity: O(N) for storing boundary nodes and auxiliary recursion stack space in the worst-case scenario of a skewed tree.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Solution

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code