Check for perfect number

Beginner Problems Basic Maths Easy

You are given an integer n. You need to check if the number is a perfect number or not. Return true if it is a perfect number, otherwise, return false.

A perfect number is a number whose proper divisors add up to the number itself.

Examples:

Input: n = 6

Output: true

Explanation: Proper divisors of 6 are 1, 2, 3.

1 + 2 + 3 = 6.

Input: n = 4

Output: false

Explanation: Proper divisors of 4 are 1, 2.

1 + 2 = 3.

Input: n = 28

Constraints

1 <= n <= 5000

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/4KtP4Y7Cmrp/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition:

Given a number, all its proper divisors (divisors that divide the number without leaving any remainder, excluding the number itself) can be found and summed up. Then, the sum can be compared with the number itself. If the sum is the same as the number, then it is a perfect number, otherwise, it is not.

Approach:

Initialize a variable with 0 to store the sum of the proper divisors.
Start iterating from 1 to the given number(excluding) using a loop variable, and check whether the number is divisible completely (leaving the remainder zero) by the loop variable.
If it is divisible completely, the current value of the loop variable is a proper divisor which is added to the sum storing sum of proper divisors.
After the sum is calculated, compare it with the given number. If found equal, the given number is perfect, otherwise, it is not.

Dry Run:

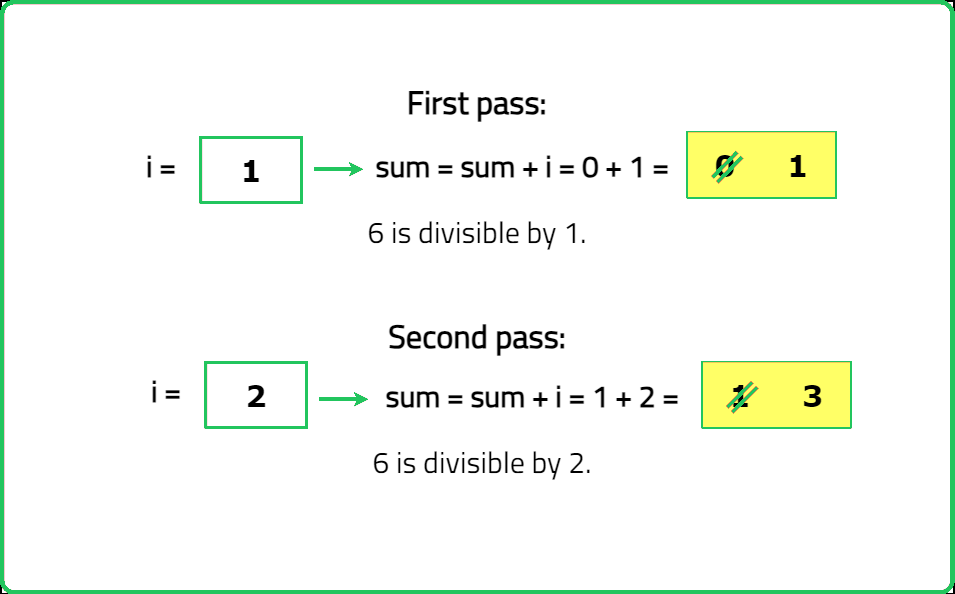
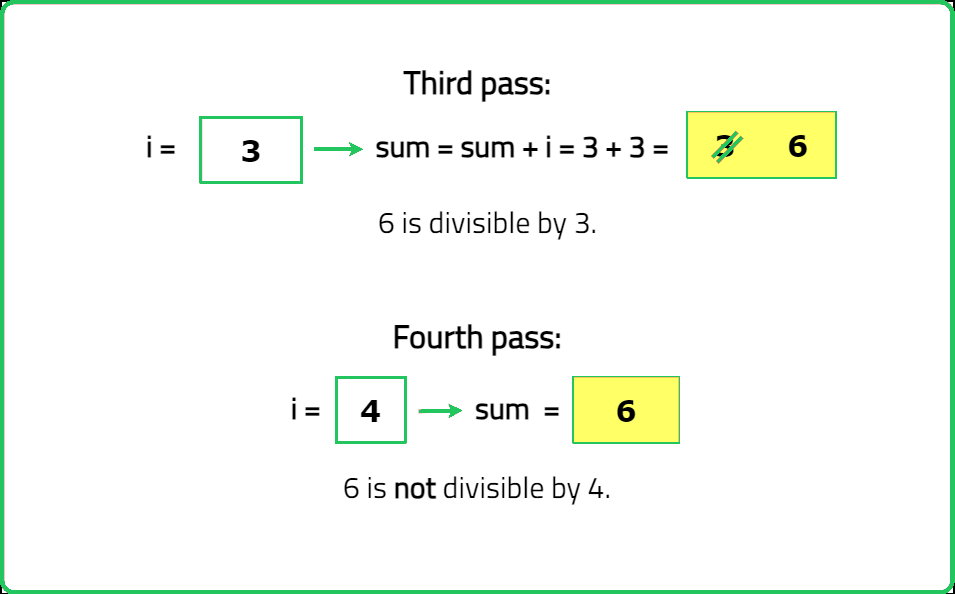
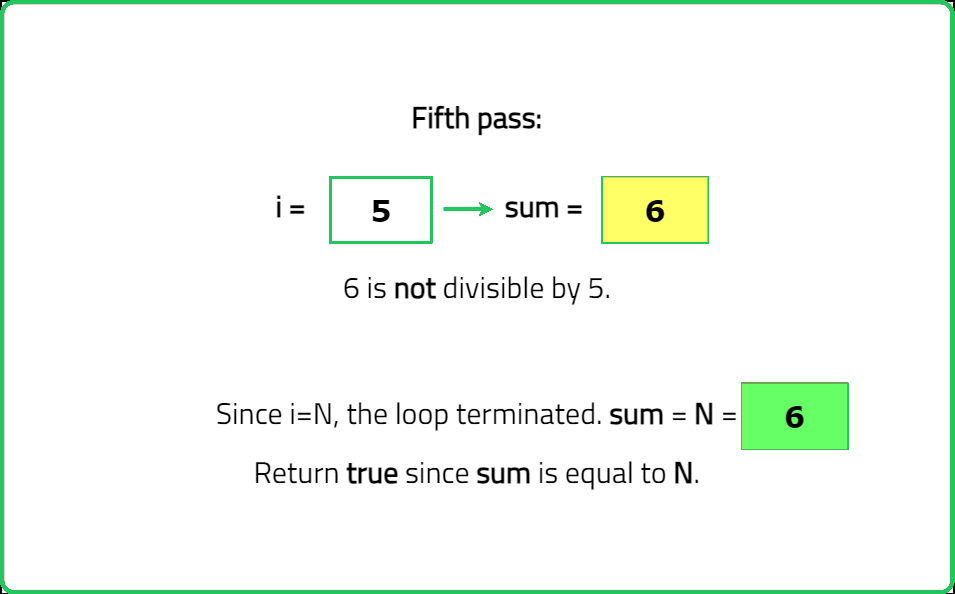
Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find whether the
    number is perfect or not */
    bool isPerfect(int n) {
        
        /* Variable to store the sum
        of all proper divisors */
        int sum = 0;
        
        // Loop from 1 to n
        for(int i=1; i < n; ++i) {
            
            // Check if i is a proper divisor
            if(n % i == 0){
                // Update sum
                sum = sum + i;
            }
        }
        
        // Compare sum and n
        if(sum == n) return true;
        return false;
    }
};

int main() {
    int n = 6;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find whether the
     given number is perfect or not */
    bool ans = sol.isPerfect(n);
    
    if(ans) {
        cout << n << " is a perfect number." << endl;
    } else {
        cout << n << " is not a perfect number." << endl;
    }
    
    return 0;
}
class Solution {
    /* Function to find whether the
    number is perfect or not */
    public boolean isPerfect(int n) {
        
        /* Variable to store the sum
        of all proper divisors */
        int sum = 0;
        
        // Loop from 1 to n
        for(int i = 1; i < n; ++i) {
            
            // Check if i is a proper divisor
            if(n % i == 0){
                // Update sum
                sum = sum + i;
            }
        }
        
        // Compare sum and n
        if(sum == n) return true;
        return false;
    }

    public static void main(String[] args) {
        int n = 6;
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to find whether the
         given number is perfect or not */
        boolean ans = sol.isPerfect(n);
        
        if(ans) {
            System.out.println(n + " is a perfect number.");
        } else {
            System.out.println(n + " is not a perfect number.");
        }
    }
}
class Solution:
    # Function to find whether the
    # number is perfect or not
    def isPerfect(self, n):
        
        # Variable to store the sum
        # of all proper divisors
        sum = 0
        
        # Loop from 1 to n
        for i in range(1, n):
            
            # Check if i is a proper divisor
            if n % i == 0:
                # Update sum
                sum = sum + i
        
        # Compare sum and n
        return sum == n

# Input number
n = 6

# Creating an instance of Solution class
sol = Solution()

# Function call to find whether the given number is perfect or not
ans = sol.isPerfect(n)

if ans:
    print(f"{n} is a perfect number.")
else:
    print(f"{n} is not a perfect number.")
class Solution {
    /* Function to find whether the
    number is perfect or not */
    isPerfect(n) {
        
        /* Variable to store the sum
        of all proper divisors */
        let sum = 0;
        
        // Loop from 1 to n
        for (let i = 1; i < n; ++i) {
            
            // Check if i is a proper divisor
            if (n % i === 0) {
                // Update sum
                sum = sum + i;
            }
        }
        
        // Compare sum and n
        return sum === n;
    }
}

// Input number
let n = 6;

// Creating an instance of Solution class
let sol = new Solution();

// Function call to find whether the given number is perfect or not
let ans = sol.isPerfect(n);

if (ans) {
    console.log(`${n} is a perfect number.`);
} else {
    console.log(`${n} is not a perfect number.`);
}

Complexity Analysis:

Time Complexity: O(N) – Running a loop from 1 to N.

Space Complexity: O(1) – Using a couple of variables i.e., constant space, regardless of the size of input.

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/4KtP4Y7Cmrp/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition:

The previous approach can be optimized by using the property that for any non-negative integer n, if d is a divisor of n then n/d is also a divisor (counterpart divisor) of n. This property is symmetric about the square root of n. By traversing just the first half, the redundant iterations and computations can be avoided improving the efficiency of the algorithm.

Approach:

Initialize a variable with 0 to store the sum of the proper divisors.
Start iterating from 1 to square root of the given number using a loop variable, and check whether the number is divisible completely (leaving the remainder zero) by the loop variable.
If it is divisible completely, the current value of the loop variable is a proper divisor which is added to the sum storing sum of proper divisors. Also, using the property discussed above, another proper divisor can be found.
Note: Before adding the counterpart divisor, it should be checked if both the proper divisors are different and the counterpart divisor is not the number itself. If they are different and the counterpart divisor is not the number itself, the counterpart divisor should be added to the sum. Otherwise, the counterpart divisor should not be added to the sum ensuring that the divisor is not added twice.
After the sum is calculated, compare it with the given number. If found equal, the given number is perfect, otherwise, it is not.

Edge Case:

When the given number is 1, there are no proper divisors of 1, i.e., the sum of proper divisors of the number is 0. Hence, 1 is not a perfect number.

Dry Run:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find whether the
    number is perfect or not */
    bool isPerfect(int n) {
        // Edge case
        if(n == 1) return false;
        
        /* Variable to store the sum
        of all proper divisors */
        int sum = 0;
        
        // Loop from 1 to square root of n
        for(int i=1; i <= sqrt(n); ++i) {
            
            // Check if i is a proper divisor
            if(n % i == 0){
                // Update sum
                sum = sum + i;
                
                /* Add the counterpart divisor
                if it's different from i and
                if it is not n itself */
                if(n/i != n && i != n/i) {
                    sum = sum + (n/i);
                }
            }
        }
        
        // Compare sum and n
        if(sum == n) return true;
        return false;
    }
};

int main() {
    int n = 6;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find whether the
     given number is perfect or not */
    bool ans = sol.isPerfect(n);
    
    if(ans) {
        cout << n << " is a perfect number." << endl;
    } else {
        cout << n << " is not a perfect number." << endl;
    }
    
    return 0;
}
class Solution {
    /* Function to find whether the
    number is perfect or not */
    public boolean isPerfect(int n) {
        // Edge case
        if(n == 1) return false;
        
        /* Variable to store the sum
        of all proper divisors */
        int sum = 0;
        
        // Loop from 1 to square root of n
        for (int i = 1; i <= Math.sqrt(n); ++i) {
            
            // Check if i is a proper divisor
            if (n % i == 0) {
                // Update sum
                sum = sum + i;
                
                /* Add the counterpart divisor
                if it's different from i and
                if it is not n itself */
                if (n / i != n && i != n / i) {
                    sum = sum + (n / i);
                }
            }
        }
        
        // Compare sum and n
        if (sum == n) return true;
        return false;
    }
}
import math

class Solution:
    # Function to find whether the 
    # number is perfect or not
    def isPerfect(self, n):
        # Edge case
        if n == 1: 
            return False
        # Variable to store the sum of all proper divisors
        sum = 0
        
        # Loop from 1 to square root of n
        for i in range(1, int(math.sqrt(n)) + 1):
            
            # Check if i is a proper divisor
            if n % i == 0:
                # Update sum
                sum = sum + i
                
                # Add the counterpart divisor if it's 
                # different from i and if it is not n itself
                if n // i != n and i != n // i:
                    sum = sum + (n // i)
        
        # Compare sum and n
        if sum == n:
            return True
        return False

if __name__ == "__main__":
    n = 6
    
    # Creating an instance of Solution class
    sol = Solution()
    
    # Function call to find whether the given number is perfect or not
    ans = sol.isPerfect(n)
    
    if ans:
        print(f"{n} is a perfect number.")
    else:
        print(f"{n} is not a perfect number.")
class Solution {
    /* Function to find whether the
    number is perfect or not */
    isPerfect(n) {
        // Edge case
        if(n === 1) 
            return false;
            
        /* Variable to store the sum
        of all proper divisors */
        let sum = 0;
        
        // Loop from 1 to square root of n
        for (let i = 1; i <= Math.sqrt(n); ++i) {
            
            // Check if i is a proper divisor
            if (n % i === 0) {
                // Update sum
                sum = sum + i;
                
                /* Add the counterpart divisor
                if it's different from i and
                if it is not n itself */
                if (n / i !== n && i !== n / i) {
                    sum = sum + (n / i);
                }
            }
        }
        
        // Compare sum and n
        if (sum === n) return true;
        return false;
    }
}

const n = 6;

/* Creating an instance of 
Solution class */
const sol = new Solution();

/* Function call to find whether the
 given number is perfect or not */
const ans = sol.isPerfect(n);

if (ans) {
    console.log(`${n} is a perfect number.`);
} else {
    console.log(`${n} is not a perfect number.`);
}

Complexity Analysis:

Time Complexity: O(sqrt(N)) – Running a loop from 1 to square root of N.

Space Complexity: O(1) – Using a couple of variables i.e., constant space, regardless of the size of input.

Code

Problem List

Check for perfect number

Examples:

Constraints

Company Tags

Editorial

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Intuition:

Approach:

Edge Case:

Dry Run:

Complexity Analysis:

Notes

Code

Facts