Single Number - II
Bit Manipulation
Problems
Medium
- This type of problem finds real-world applications in data analytics and cybersecurity
- Companies often maintain log files for user activities for analysis
- Most users will repeat certain activities multiple times, but some unusual activities (like a potential security breach) might only appear once
- An algorithm that can efficiently identify these one-time events can alarm security systems about potential threats, triggering necessary preventive actions
Given an array nums where each integer in nums appears thrice except one. Find out the number that has appeared only once.
Examples:
Input : nums = [2, 2, 2, 3]
Output : 3
Explanation : The integers 3 has appeared only once.
Input : nums = [1, 0, 3, 0, 1, 1, 3, 3, 10, 0]
Output : 10
Explanation : The integers 10 has appeared only once.
Input : nums = [5, 0, 1, 10, 1, 1, 5, 5, 10, 10]
Constraints
- 1 <= n <= 3*104
- -231 <= nums[i] <= 231 - 1
Hints
- For each bit position (0 to 31), traverse the array and count how many numbers have that bit set to 1. Use the modulo operation (count % 3) to identify whether the unique number has that bit set.
- After computing the bit values for all positions, combine them to form the unique number. Ensure you handle negative numbers correctly by checking the most significant bit.
Company Tags
Airbnb
Stripe
Electronic Arts
Optum
Docker
Western Digital
Medtronic
Epic Games
Zomato
Dropbox
Cerner
eBay
Deloitte
Nutanix
Micron Technology
Square
Bungie
Byju's
ARM
Wayfair
Instacart
Databricks
Roblox
JPMorgan Chase
KPMG
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The brute force way to solve this will be to utilize a frequency counting approach. By keeping track of the frequency of each element in the array, the element that appears only once can be easily identified.
Approach:
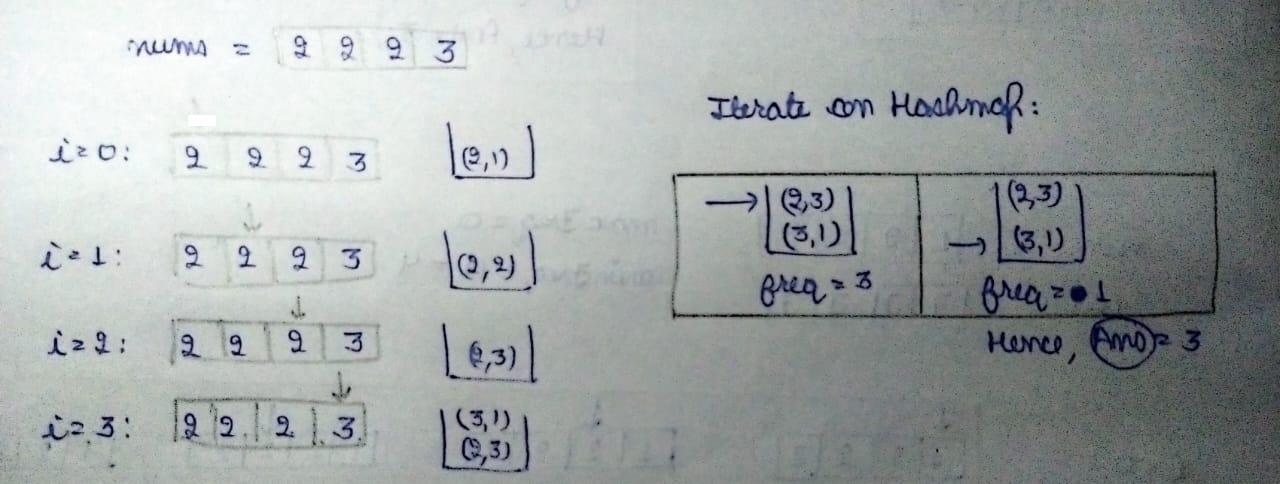
- Use a hash map to store the frequency of each element in the array. The keys of the map are the elements of the array, and the values are their corresponding frequencies.
- Traverse the entire array once, and for each element, update its frequency count in the map.
- After populating the map with frequency counts, iterate over the map to find the element with a frequency of 1. This element is the unique integer that appears only once in the array.
- Return the unique element found in the map. If no such element exists (though the problem guarantees that one does), return -1.
---!>
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to get the single
number in the given array */
int singleNumber(vector<int>& nums){
/* Map to store the elements
and their frequencies */
unordered_map <int, int> mpp;
// Iterate on the array
for(int i=0; i < nums.size(); i++) {
mpp[nums[i]]++; //Update the map
}
//Iterate on the map
for(auto it : mpp) {
// If frequency is 1
if(it.second == 1) {
// Return the element
return it.first;
}
}
/* Return -1, if there is no
number having frequency 1 */
return -1;
}
};
int main() {
vector<int> nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
cout << "The single number in given array is: " << ans;
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445
import java.util.HashMap;
class Solution {
/* Function to get the single
number in the given array */
public int singleNumber(int[] nums) {
/* Map to store the elements
and their frequencies */
HashMap<Integer, Integer> mpp = new HashMap<>();
// Iterate on the array
for (int i = 0; i < nums.length; i++) {
mpp.put(nums[i], mpp.getOrDefault(nums[i], 0) + 1); // Update the map
}
// Iterate on the map
for (HashMap.Entry<Integer, Integer> it : mpp.entrySet()) {
// If frequency is 1
if (it.getValue() == 1) {
// Return the element
return it.getKey();
}
}
/* Return -1, if there is no
number having frequency 1 */
return -1;
}
public static void main(String[] args) {
int[] nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
System.out.println("The single number in given array is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435
class Solution:
# Function to get the single
# number in the given array
def singleNumber(self, nums):
# Map to store the elements
# and their frequencies
mpp = {}
# Iterate on the array
for num in nums:
mpp[num] = mpp.get(num, 0) + 1 # Update the map
# Iterate on the map
for key, value in mpp.items():
# If frequency is 1
if value == 1:
# Return the element
return key
# Return -1, if there is no
# number having frequency 1
return -1
# Test the function
nums = [2, 2, 2, 3]
# Creating an instance of Solution class
sol = Solution()
# Function call to get the single number in the given array
ans = sol.singleNumber(nums)
print("The single number in given array is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142
class Solution {
/* Function to get the single
number in the given array */
singleNumber(nums) {
/* Map to store the elements
and their frequencies */
let mpp = new Map();
// Iterate on the array
for (let i = 0; i < nums.length; i++) {
mpp.set(nums[i], (mpp.get(nums[i]) || 0) + 1); // Update the map
}
// Iterate on the map
for (let [key, value] of mpp.entries()) {
// If frequency is 1
if (value === 1) {
// Return the element
return key;
}
}
/* Return -1, if there is no
number having frequency 1 */
return -1;
}
}
// Test the function
let nums = [2, 2, 2, 3];
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to get the single
number in the given array */
let ans = sol.singleNumber(nums);
console.log("The single number in given array is: " + ans);
Complexity Analysis:
Time Complexity: O(N) (where N is the size of the array) –
Space Complexity: O(N) – Using a hashmap data structure and in the worst-case (when all elements in the array are unique), it will store N key-value pairs.
Intuition:
A better approach would be to use the properties of binary representation and bit manipulation. The idea is to count the bits at each position.
For elements appearing three times, the bit count will be a multiple of three. The unique element's bit will not follow this pattern, using which it could be identified.
Approach:
- Start by initializing a variable to store the result, which will eventually hold the unique element.
- Loop through each bit position (from 0 to 31, assuming 32-bit integers) to examine the contribution of each bit across all numbers in the array.
- For each bit position, count how many numbers in the array have a set bit (bit value of 1) at that specific position.
- For each bit position, if the count of set bits is not a multiple of three, it means the unique element has a set bit at that position.
- Update the result variable by setting the corresponding bit position where the count of set bits is not a multiple of three.
- After processing all bit positions, the result variable will contain the unique element that appears only once in the array.
---!>
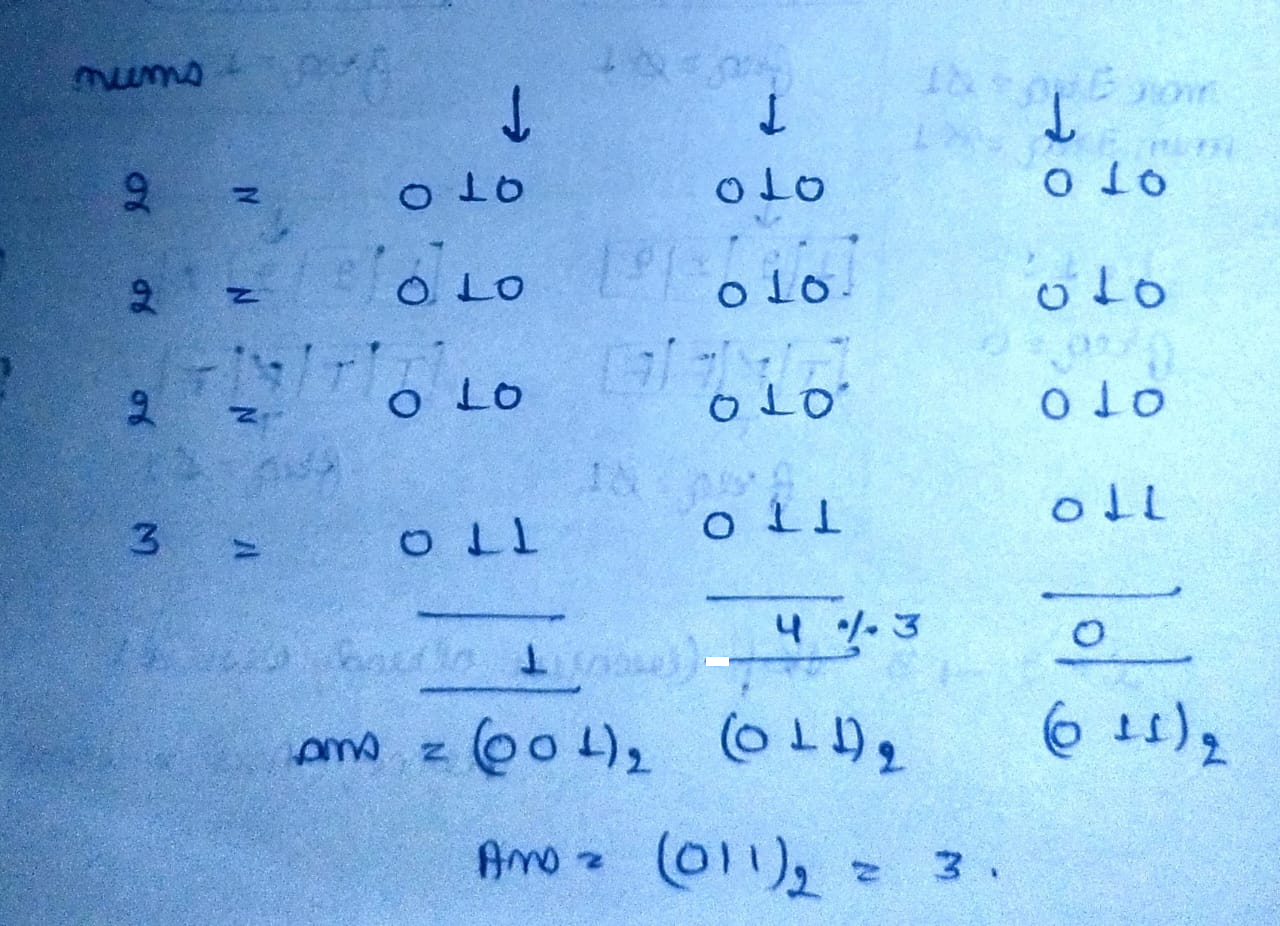Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to get the single
number in the given array */
int singleNumber(vector<int>& nums){
// Variable to store size of array
int n = nums.size();
// Variable to store the ans
int ans = 0;
// Checking every bit position
for(int bitIndex = 0; bitIndex < 32; bitIndex++) {
/* Variable to count number of
set bits in bitIndex position */
int count = 0;
// Traversing all elements
for(int i = 0; i < n; i++) {
/* Counting elements having set
bits at bitIndex position */
if(nums[i] & (1 << bitIndex)) {
count++;
}
}
// Updating bits in answer
if(count % 3 != 0) {
ans |= (1 << bitIndex);
}
}
return ans;
}
};
int main() {
vector<int> nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
cout << "The single number in given array is: " << ans;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
import java.util.*;
class Solution {
/* Function to get the single
number in the given array */
public int singleNumber(int[] nums) {
// Variable to store size of array
int n = nums.length;
// Variable to store the ans
int ans = 0;
// Checking every bit position
for (int bitIndex = 0; bitIndex < 32; bitIndex++) {
/* Variable to count number of
set bits in bitIndex position */
int count = 0;
// Traversing all elements
for (int i = 0; i < n; i++) {
/* Counting elements having set
bits at bitIndex position */
if ((nums[i] & (1 << bitIndex)) != 0) {
count++;
}
}
// Updating bits in answer
if (count % 3 != 0) {
ans |= (1 << bitIndex);
}
}
return ans;
}
public static void main(String[] args) {
int[] nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
System.out.println("The single number in given array is: " + ans);
}
}1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution:
# Function to get the single
# number in the given array
def singleNumber(self, nums):
# Variable to store the ans
ans = 0
# Checking every bit position
for bitIndex in range(32):
# Variable to count number of
# set bits in bitIndex position
count = 0
# Traversing all elements
for num in nums:
# Counting elements having set
# bits at bitIndex position
if num & (1 << bitIndex):
count += 1
# Updating bits in answer
if count % 3 != 0:
ans |= (1 << bitIndex)
# Handling negative numbers
if ans >= 2**31: # If the sign bit is set
ans -= 2**32
return ans
if __name__ == "__main__":
nums = [2, 2, 2, 3]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to get the single
# number in the given array
ans = sol.singleNumber(nums)
print("The single number in the given array is:", ans)12345678910111213141516171819202122232425262728293031323334353637383940414243444546
class Solution {
/* Function to get the single
number in the given array */
singleNumber(nums) {
// Variable to store the ans
let ans = 0;
// Checking every bit position
for (let bitIndex = 0; bitIndex < 32; bitIndex++) {
/* Variable to count number of
set bits in bitIndex position */
let count = 0;
// Traversing all elements
for (let i = 0; i < nums.length; i++) {
/* Counting elements having set
bits at bitIndex position */
if (nums[i] & (1 << bitIndex)) {
count++;
}
}
// Updating bits in answer
if (count % 3 != 0) {
ans |= (1 << bitIndex);
}
}
return ans;
}
}
const nums = [2, 2, 2, 3];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to get the single
number in the given array */
const ans = sol.singleNumber(nums);
console.log("The single number in given array is:", ans);
Complexity Analysis:
Time Complexity: O(32*N) – For every 32-bit position, all the elements of the array are traversed.
Space Complexity: O(1) – Using a couple of variables i.e., constant space.
Intuition:
The most optimal way to solve this problem is by grouping (forming buckets) all the identical elements which can be done by sorting the array.
Now, the question of finding the single number will boil down to check for the number that doesn't follow the pattern of appearing three times consecutively.
Approach:
- First, sort the given array. Sorting helps in grouping the numbers that appear three times consecutively, making it easier to identify the single number.
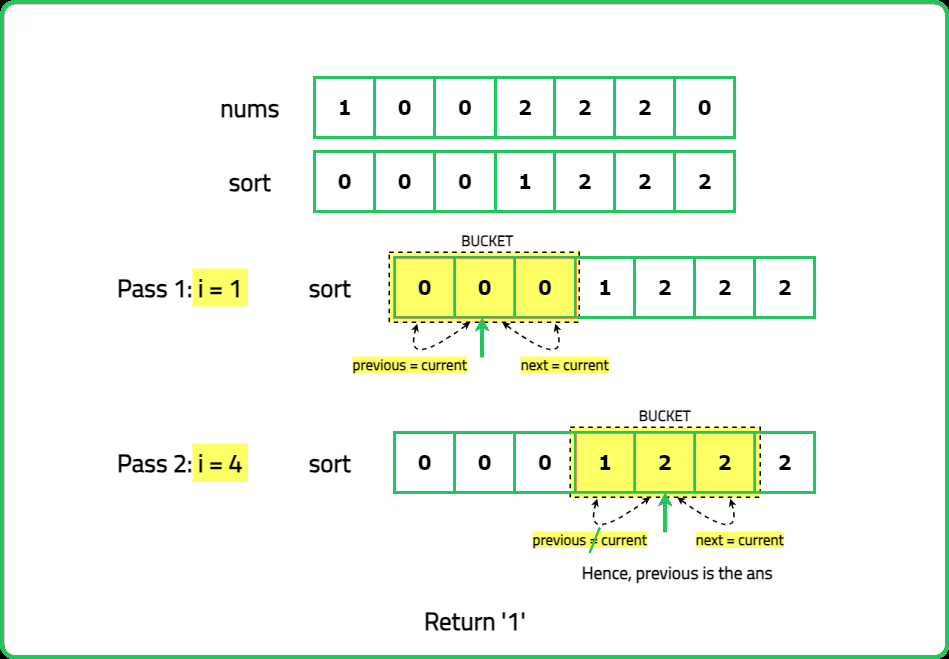
- Start traversing the sorted array and check every third element starting from the first. Compare it with the previous element.
- If the current element is different from the previous one, the previous element is the single number.
- Since the array is sorted, the first number in any group of three will be different from the single number.
- Return the identified single number.
Edge Case:
What if there is no single number found in the array during traversal?
The single number must be the last element in the array because the array is sorted, and all other elements would have been grouped by threes.
Dry Run:
Solution:
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to get the single
number in the given array */
int singleNumber(vector<int>& nums) {
// Variable to store size of array
int n = nums.size();
// Sorting the array
sort(nums.begin(), nums.end());
// Traversing the array
for (int i = 1; i < nums.size(); i += 3) {
/* Checking the elements
in the bucket */
if (nums[i] != nums[i - 1]) {
// Return the single number
return nums[i - 1];
}
}
/* If not found till now, then
the last number will be single */
return nums[n - 1];
}
};
int main() {
vector<int> nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
cout << "The single number in given array is: " << ans;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142
import java.util.Arrays;
class Solution {
/* Function to get the single
number in the given array */
public int singleNumber(int[] nums) {
// Variable to store size of array
int n = nums.length;
// Sorting the array
Arrays.sort(nums);
// Traversing the array
for (int i = 1; i < nums.length; i += 3) {
/* Checking the elements
in the bucket */
if (nums[i] != nums[i - 1]) {
// Return the single number
return nums[i - 1];
}
}
/* If not found till now, then
the last number will be single */
return nums[n - 1];
}
public static void main(String[] args) {
int[] nums = {2, 2, 2, 3};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to get the single
number in the given array */
int ans = sol.singleNumber(nums);
System.out.println("The single number in given array is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435
class Solution:
""" Function to get the single
number in the given array """
def singleNumber(self, nums):
# Variable to store size of array
n = len(nums)
# Sorting the array
nums.sort()
# Traversing the array
for i in range(1, len(nums), 3):
""" Checking the elements
in the bucket """
if nums[i] != nums[i - 1]:
# Return the single number
return nums[i - 1]
""" If not found till now, then
the last number will be single """
return nums[n - 1]
# Example usage
nums = [2, 2, 2, 3]
""" Creating an instance of
Solution class """
sol = Solution()
""" Function call to get the single
number in the given array """
ans = sol.singleNumber(nums)
print("The single number in given array is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839
class Solution {
/* Function to get the single
number in the given array */
singleNumber(nums) {
// Variable to store size of array
let n = nums.length;
// Sorting the array
nums.sort((a, b) => a - b);
// Traversing the array
for (let i = 1; i < nums.length; i += 3) {
/* Checking the elements
in the bucket */
if (nums[i] != nums[i - 1]) {
// Return the single number
return nums[i - 1];
}
}
/* If not found till now, then
the last number will be single */
return nums[n - 1];
}
}
// Example usage
let nums = [2, 2, 2, 3];
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to get the single
number in the given array */
let ans = sol.singleNumber(nums);
console.log("The single number in given array is:", ans);
Complexity Analysis:
Time Complexity: O(Nlog(N)) –
Space Complexity: O(1) Using a couple of variables i.e., constant space.
Intuition:
The intuition for this approach may not be straightforward and is not typically required in interviews.
The goal is to identify the number that appears only once in an array where all other numbers appear exactly three times. Several observations can help solve this problem.
Imagine using three buckets named Ones, Twos, and Threes to keep track of numbers that appear once, twice, and thrice respectively while iterating through the array. These observations can be made:
- A number can be added to Ones if it is not already in Twos.
- A number can be added to Twos if it is already in Ones.
- A number can be added to Threes if it is already in Twos.
This leads to the idea of using three variables to represent the three buckets and applying bit manipulation to add or remove numbers from the respective buckets efficiently.
Understanding:
To add and remove numbers from the buckets, bit manipulation is employed. Among the three basic operations (&, |, ^), the XOR (^) operation is particularly useful as it facilitates both addition and removal. While traversing the array, there are three possible scenarios:
- When the number is not in Twos: If the number is not in Twos, it indicates that this is the first occurrence of the number, so it should be added to the Ones bucket. This can be expressed as:
Ones = (Ones ^ num) & ~Twos; - When the number is already in Ones: If the number is in Ones, it means it is being encountered for the second time. In this case, the number should be removed from Ones and added to the Twos bucket. This can be expressed as:
Twos = (Twos ^ num) & ~Ones; - When the number is already in Twos: If the number is in Twos, it indicates a third occurrence. In this case, the number should be removed from both Ones and Twos. However, As we are concerned about the number that appears only once, we need not to store the third bucket Threes.
Result:
After processing all numbers in the array, the first bucket (ones) contains the bits of the number that appears only once. This is because:- Bitwise XOR (^): This toggles the bits. It adds a number to the bucket if it’s not already there and removes it if it is. Numbers appearing an even number of times cancel themselves out, while the number appearing once remains.
- Bitwise AND with complement (& ~): This clears a number from the first bucket (ones) when it’s added to the second bucket (twos) or when numbers appear three times.
At the end, the first bucket retains the number that appeared exactly once, and this value is returned.
Approach:
- Initialize two variables to represent two buckets for tracking numbers that have appeared once and twice.
- Traverse the array, updating the buckets using bitwise operations:
- Add the current number to the first bucket if it is not already in the second bucket.
- Add the current number to the second bucket if it is already in the first bucket.
- Ensure that numbers appearing three times are removed from both buckets by leveraging the properties of bitwise operations.
- After processing all numbers, the first bucket holds the number that appears only once. Return this value.
Solution:
1234567891011121314151617181920212223242526272829303132333435363738
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to return the number that appears only once
int singleNumber(vector<int>& nums) {
// Two buckets
int ones = 0, twos = 0;
// Traverse the array
for(int i=0; i < nums.size(); i++) {
// Add the number to Ones, it is not in Twos
ones = (ones ^ nums[i]) & ~twos;
// Add the number to Twos, if it is already in Ones
twos = (twos ^ nums[i]) & ~ones;
}
return ones;
}
};
int main() {
vector<int> nums = {1, 0, 3, 0, 1, 1, 3, 3, 10, 0};
// Creating an instance of Solution class
Solution sol;
// Function call to find the number that appears only once
int ans = sol.singleNumber(nums);
cout << "The single number(II) is: " << ans << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233
import java.util.*;
class Solution {
public int singleNumber(int[] nums) {
// Two buckets
int ones = 0, twos = 0;
// Traverse the array
for (int i = 0; i < nums.length; i++) {
// Add the number to Ones, if it is not in Twos
ones = (ones ^ nums[i]) & ~twos;
// Add the number to Twos, if it is already in Ones
twos = (twos ^ nums[i]) & ~ones;
}
return ones;
}
}
class Main {
public static void main(String[] args) {
int[] nums = {1, 0, 3, 0, 1, 1, 3, 3, 10, 0};
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to find the number that appears only once
int ans = sol.singleNumber(nums);
System.out.println("The single number(II) is: " + ans);
}
}1234567891011121314151617181920212223242526
class Solution:
def singleNumber(self, nums):
# Two buckets
ones, twos = 0, 0
# Traverse the array
for num in nums:
# Add the number to Ones, if it is not in Twos
ones = (ones ^ num) & ~twos
# Add the number to Twos, if it is already in Ones
twos = (twos ^ num) & ~ones
return ones
# Main function
if __name__ == "__main__":
nums = [1, 0, 3, 0, 1, 1, 3, 3, 10, 0]
# Creating an instance of Solution class
sol = Solution()
# Function call to find the number that appears only once
ans = sol.singleNumber(nums)
print("The single number(II) is:", ans)12345678910111213141516171819202122232425262728
class Solution {
singleNumber(nums) {
// Two buckets
let ones = 0, twos = 0;
// Traverse the array
for (let i = 0; i < nums.length; i++) {
// Add the number to Ones, if it is not in Twos
ones = (ones ^ nums[i]) & ~twos;
// Add the number to Twos, if it is already in Ones
twos = (twos ^ nums[i]) & ~ones;
}
return ones;
}
}
// Main function
const nums = [1, 0, 3, 0, 1, 1, 3, 3, 10, 0];
// Creating an instance of Solution class
const sol = new Solution();
// Function call to find the number that appears only once
const ans = sol.singleNumber(nums);
console.log("The single number(II) is:", ans);Complexity Analysis:
Time Complexity: O(N), where N is the number of elements in the array
Traversing the array once takes linear time.
Space Complexity: O(1), as only a couple of variables are used.
Frequently Occurring Doubts
Q: Why can't XOR alone solve this problem?
A: XOR works for cases where every number appears twice except one. However, when numbers appear thrice, XOR fails because it doesn’t account for the triplet elimination logic. Instead, bitwise counting ensures the triplet property is respected.
Q: How does modulo 3 eliminate numbers that appear thrice?
A: For any bit position, the contribution of numbers appearing thrice sums to a multiple of 3. The unique number's contribution remains after applying modulo 3, isolating its bit value.
Interview Followup Questions
Q: How would you extend this to handle numbers appearing k-times except one?
A: Modify the approach to count bit frequencies and use modulo k instead of 3 to identify the unique number's bits.
Q: What if multiple numbers appear only once instead of one?
A: The current approach wouldn’t work. For m unique numbers, you’d need to modify the solution to find all such numbers, possibly using a hash set or other data structures.
Notes
Code
✅ Testcase
Input: {'nums': '[2, 2, 2, 3]'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[1, 0, 3, 0, 1, 1, 3, 3, 10, 0]'}
Expected:
10
10
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[1, 1, 1, 2, 3, 3, 3, 5, 5, 5]'}
Expected:
2
2
Actual: -
Time: -
sec
Status: Waiting