Sum of first N numbers

Beginner Problems Basic Recursion Easy

Fun Fact: The concept of summing up the first N natural numbers is often used in the development of performance analysis and benchmarking tools
These tools help developers understand the performance of their software by simulating a series of operations, such as calculating how long it takes to sum up a series of numbers, and then analyze the time complexity
The principle also has real-world usages in databases when dealing with sequence generation or serial numbers, and in building progress bar logic in numerous softwares or apps

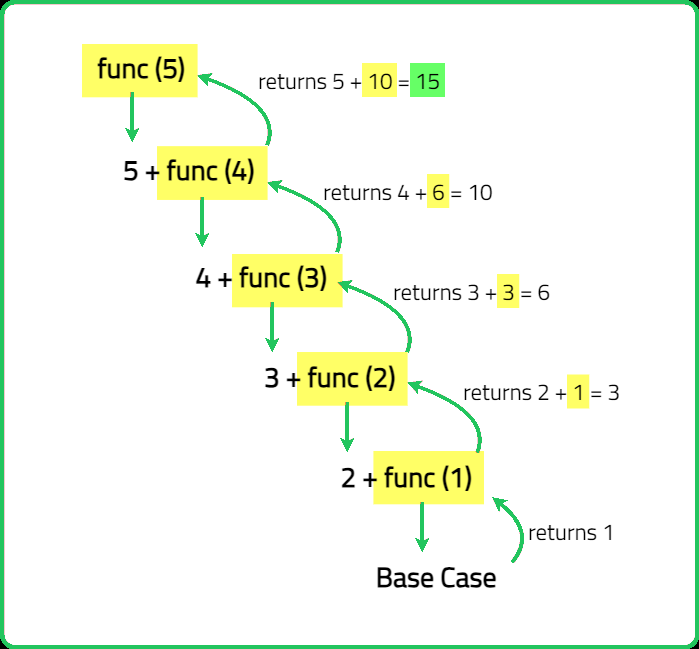
Given an integer N, return the sum of first N natural numbers. Try to solve this using recursion.

Examples:

Input : N = 4

Output : 10

Explanation : first four natural numbers are 1, 2, 3, 4.

Sum is 1 + 2 + 3 + 4 => 10.

Input : N = 2

Output : 3

Explanation : first two natural numbers are 1, 2.

Sum is 1 + 2 => 3.

Input : N = 10

Constraints

1 <= N <= 10³

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intuition

To find the sum of the first N numbers, the concept of recursion can be utilized by breaking down the problem into smaller subproblems. This involves repeatedly adding the current number to the sum of all previous numbers. The process continues until reaching the base case, where N is 0, which terminates the recursion.

Approach

Define a recursive function that returns 0 when N is 0 (base case).
For any other N, return N plus the recursive call with N − 1.
The sum is accumulated as the recursion unwinds from N down to 0.

Dry Run

Solution

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int NnumbersSum(int N) {
        // Base case: if N is 0, return 0
        if (N == 0) return 0;
        // Recursive case: add N to the sum of N-1
        return N + NnumbersSum(N - 1);
    }
};

int main() {
    Solution solution;
    int N = 10; // Example input
    cout << "Sum of first " << N << " numbers is " << solution.NnumbersSum(N) << endl;
    return 0;
}
class Solution {
    public int NnumbersSum(int N) {
        // Base case: if N is 0, return 0
        if (N == 0) return 0;
        // Recursive case: add N to the sum of N-1
        return N + NnumbersSum(N - 1);
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int N = 10; // Example input
        System.out.println("Sum of first " + N + " numbers is " + solution.NnumbersSum(N));
    }
}
class Solution:
    def NnumbersSum(self, N):
        # Base case: if N is 0, return 0
        if N == 0:
            return 0
        # Recursive case: add N to the sum of N-1
        return N + self.NnumbersSum(N - 1)

if __name__ == "__main__":
    solution = Solution()
    N = 10 # Example input
    print(f"Sum of first {N} numbers is {solution.NnumbersSum(N)}")
class Solution {
    NnumbersSum(N) {
        // Base case: if N is 0, return 0
        if (N === 0) return 0;
        // Recursive case: add N to the sum of N-1
        return N + this.NnumbersSum(N - 1);
    }
}

const solution = new Solution();
const N = 10; // Example input
console.log(`Sum of first ${N} numbers is ${solution.NnumbersSum(N)}`);

Complexity Analysis

Time Complexity O(N) — The function makes N recursive calls to reach the base case, so the time complexity is proportional to the number of calls made

Space Complexity O(N) — In the worst case, the recursion stack space would be full with all the function calls waiting to get completed and that would make it an O(N) recursion stack space

Code

Problem List