Celebrity Problem
Stack / Queues
FAQs
Hard
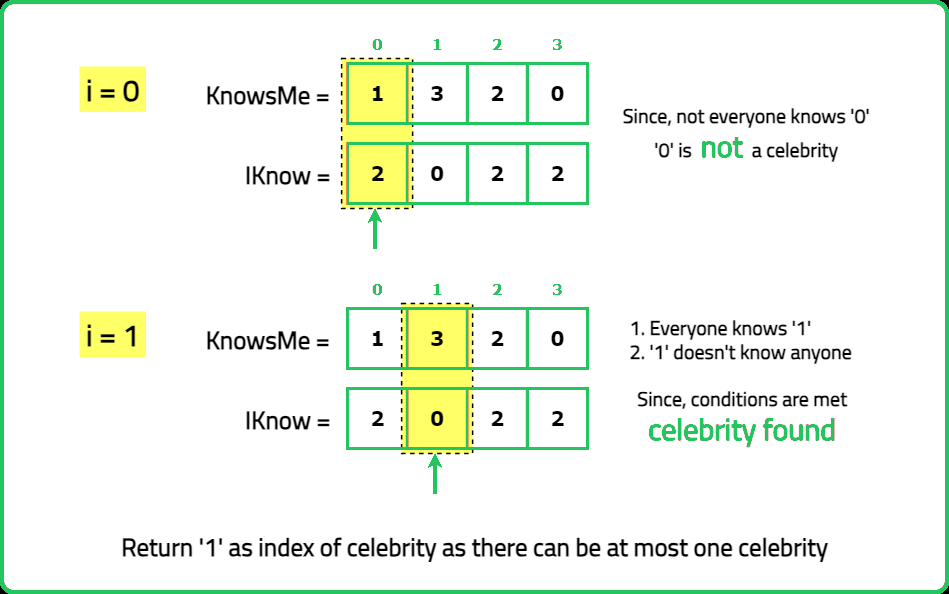
A celebrity is a person who is known by everyone else at the party but does not know anyone in return. Given a square matrix M of size N x N where M[i][j] is 1 if person i knows person j, and 0 otherwise, determine if there is a celebrity at the party. Return the index of the celebrity or -1 if no such person exists.
Note that M[i][i] is always 0.
Examples:
Input: M = [ [0, 1, 1, 0], [0, 0, 0, 0], [1, 1, 0, 0], [0, 1, 1, 0] ]
Output: 1
Explanation: Person 1 does not know anyone and is known by persons 0, 2, and 3. Therefore, person 1 is the celebrity.
Input: M = [ [0, 1], [1, 0] ]
Output: -1
Explanation: Both persons know each other, so there is no celebrity.
Input: M = [ [0, 1, 0], [0, 0, 0], [0, 1, 0] ]
Constraints
- 1 <= N <= 3000
- 0 <= M[][] <= 1
Hints
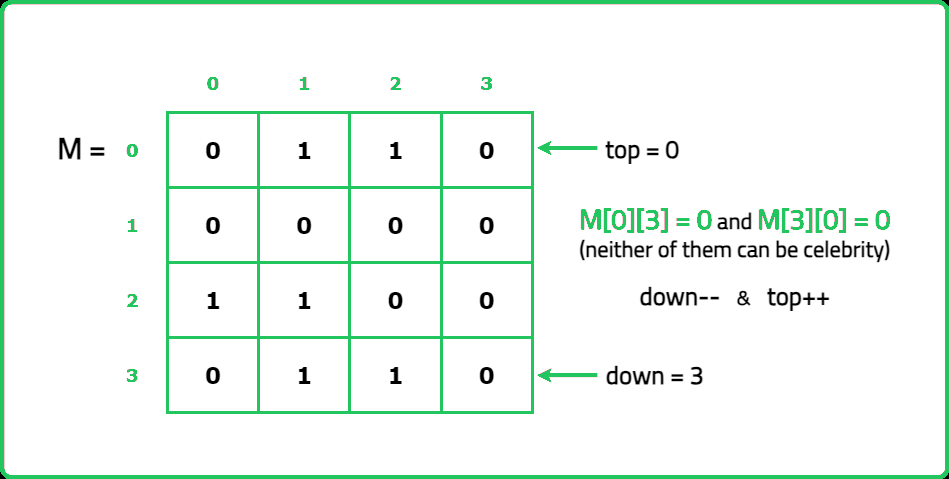
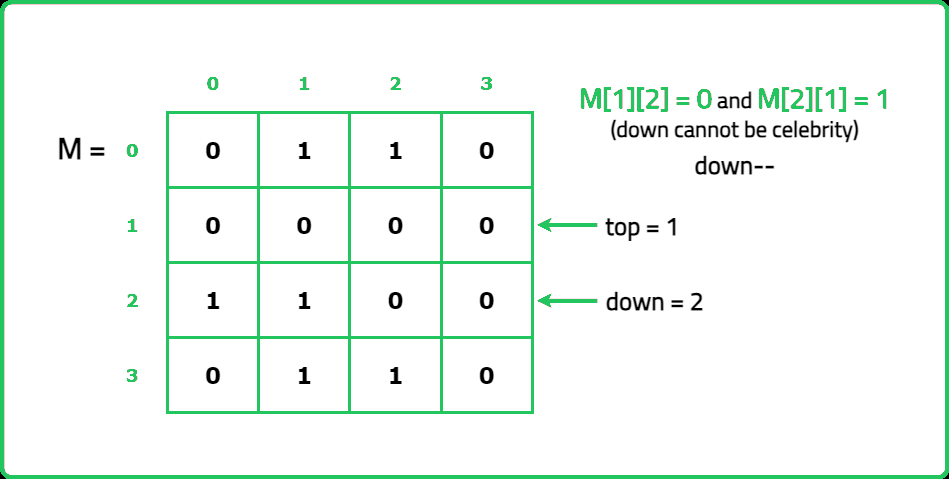
- Start with two pointers, left = 0 and right = N-1. Compare M[left][right]: If M[left][right] = 1 → left knows right, so left cannot be a celebrity → move left forward. Else → right cannot be a celebrity → move right backward. At the end of this step, we have one candidate.
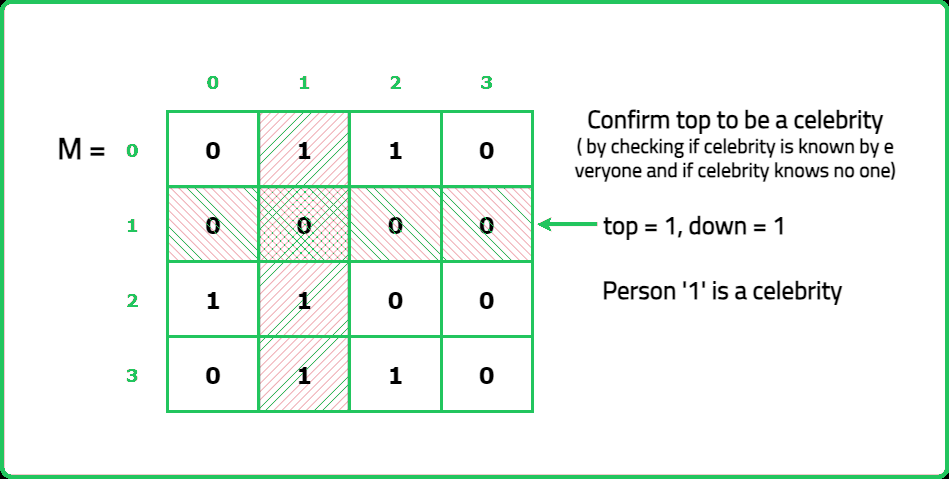
- Check if the candidate satisfies both conditions: Row Check: M[candidate][j] should be 0 for all j ≠ candidate. (Candidate knows no one). Column Check: M[i][candidate] should be 1 for all i ≠ candidate. (Everyone knows the candidate).
Company Tags
Medtronic
Nutanix
Deloitte
Stripe
Johnson & Johnson
Airbnb
HashiCorp
Visa
Zoho
Cerner
Ubisoft
Swiggy
Red Hat
Square
Activision Blizzard
IBM
Chewy
Twilio
Dropbox
ARM
DoorDash
JPMorgan Chase
KPMG
Databricks
MongoDB
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe