Rotate string
Beginner Problems
Basic Strings
Easy
- Fun fact: The concept of string shifting like in this problem is actually used in certain types of encryption and decryption algorithms, especially in the field of cybersecurity
- This concept is also used in implementing certain functions of text editors and data processing tools, where words, sentences, or paragraphs need to be shifted or rearranged
- Solving such problems helps programmers in understanding how to manipulate and process strings effectively, which is a fundamental aspect in fields such as data management, web development, and more
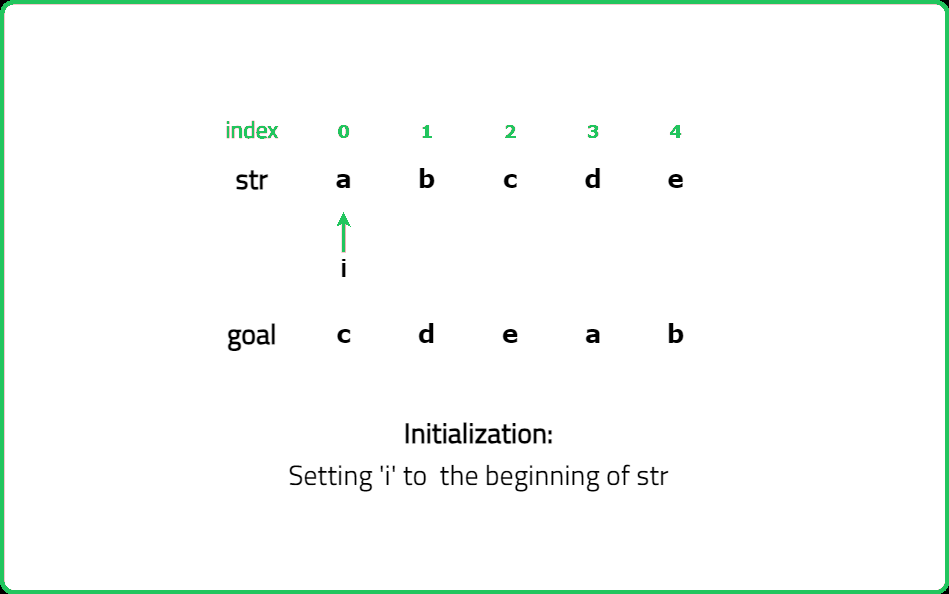
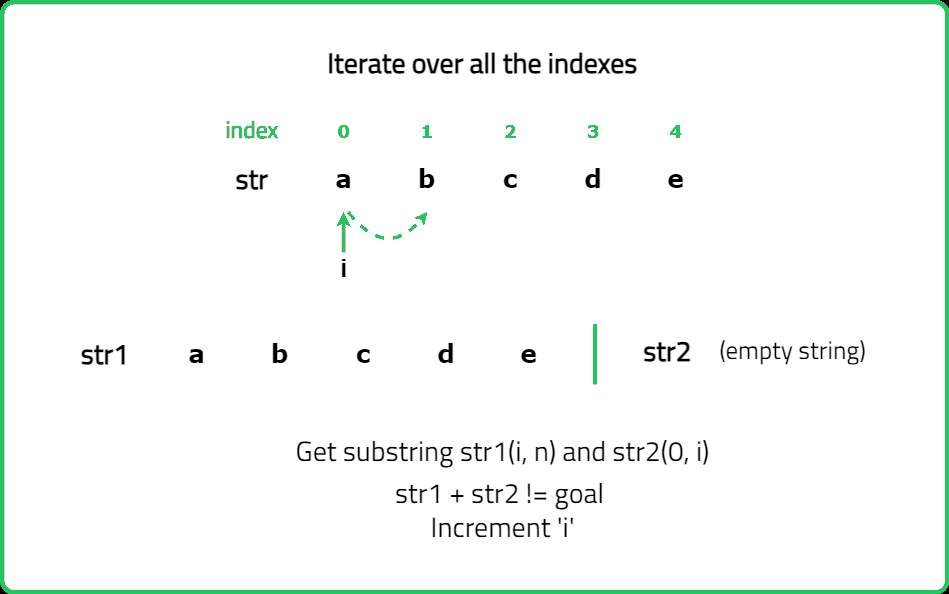
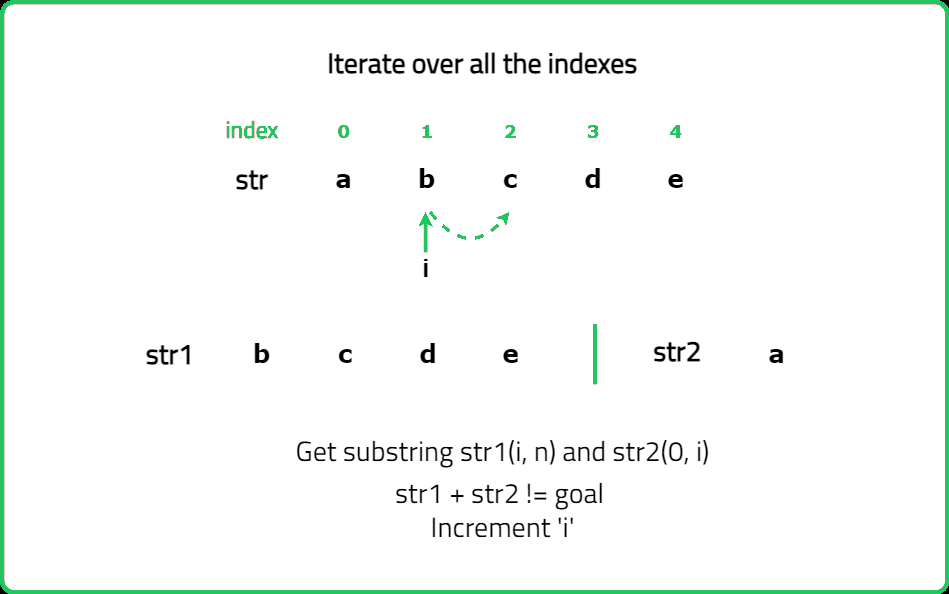
Given two strings s and goal, return true if and only if s can become goal after some number of shifts on s.
A shift on s consists of moving the leftmost character of s to the rightmost position.
For example, if s = "abcde", then it will be "bcdea" after one shift.
Examples:
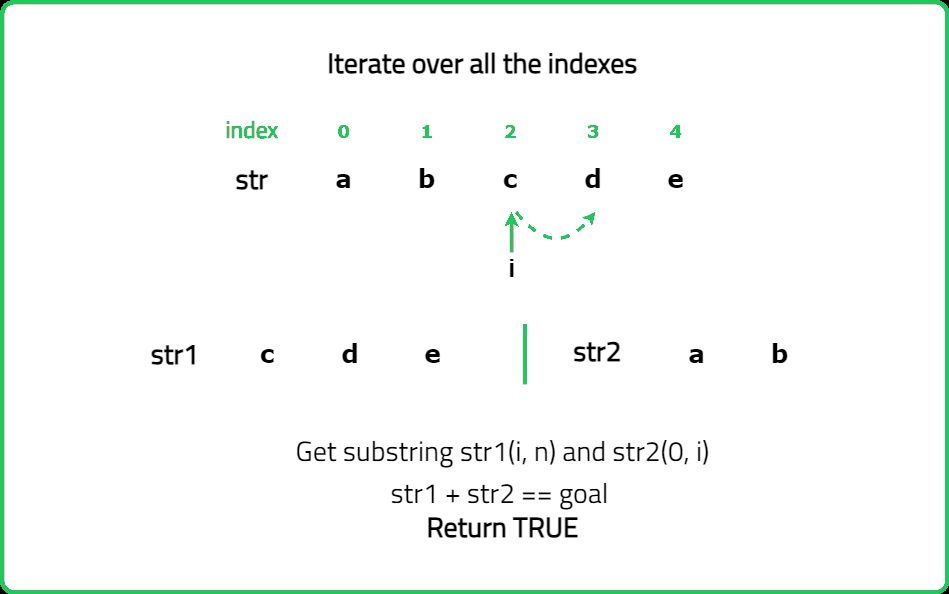
Input : s = "abcde" , goal = "cdeab"
Output : true
Explanation : After performing 2 shifts we can achieve the goal string from string s.
After first shift the string s is => bcdea
After second shift the string s is => cdeab.
Input : s = "abcde" , goal = "adeac"
Output : false
Explanation : Any number of shift operations cannot convert string s to string goal.
Input : s = "abcde" , goal = "abcde"
Constraints
- 1 <= s.length <= 100
- 1 <= goal.length <= 100
- s and goal consist of only lowercase English letters.
Company Tags
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro
IBM
HCL
Tech Mahindra
MindTree