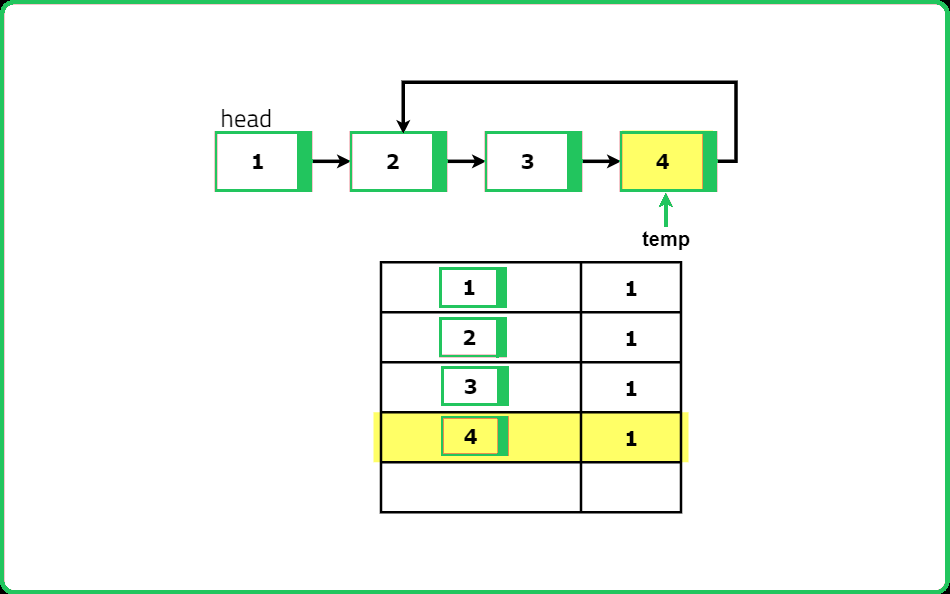
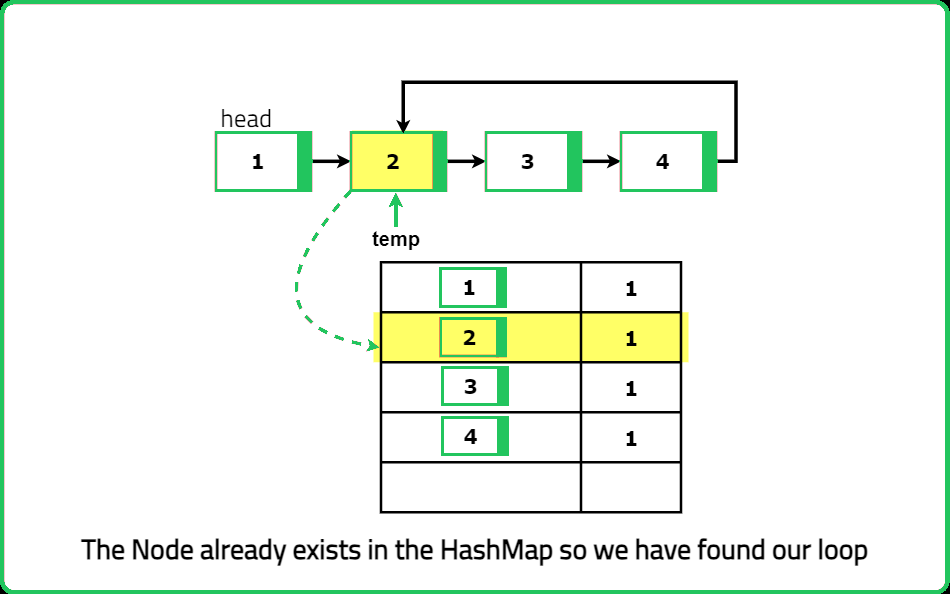
Intuition
The previous method utilizes O(N) additional memory, which can be of concern when dealing with longer linked lists. To improve efficiency, we can use the Tortoise and Hare Algorithm, which is an optimized approach that reduces memory usage. This algorithm uses two pointers moving at different speeds to detect loops more efficiently.
Approach
Initialization:
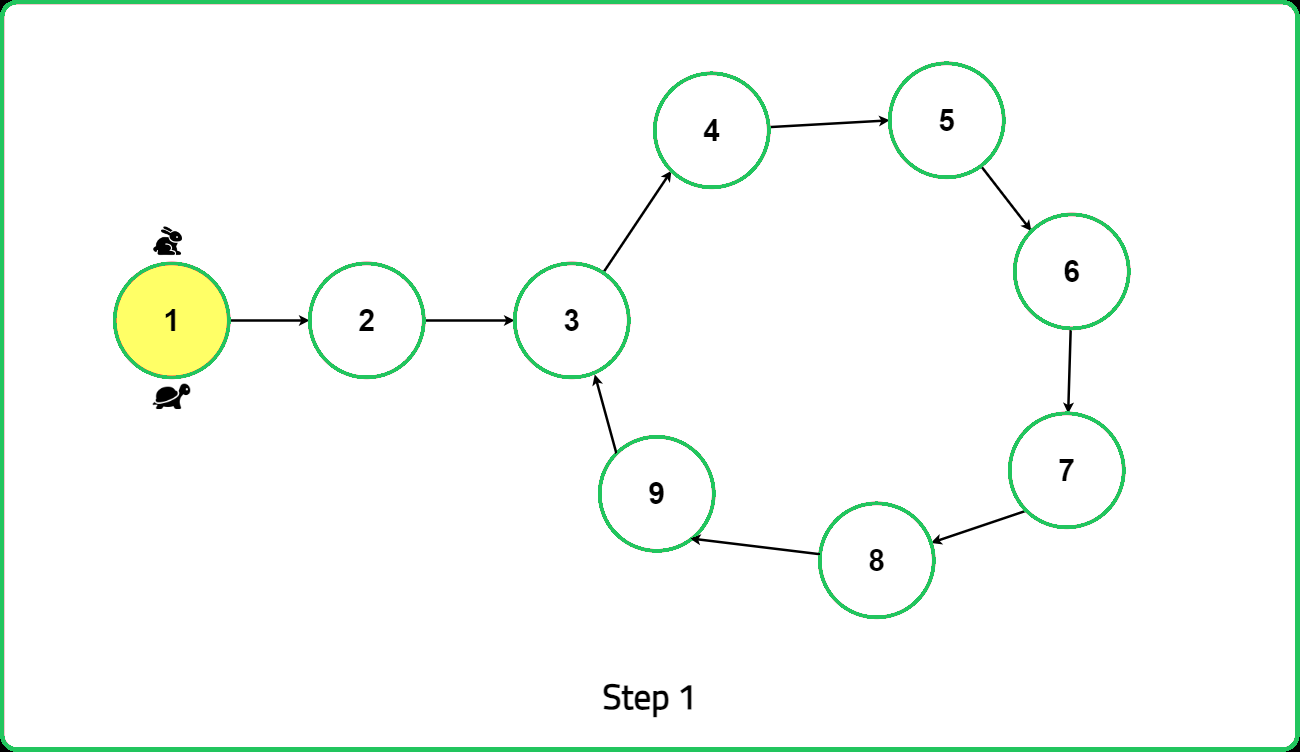
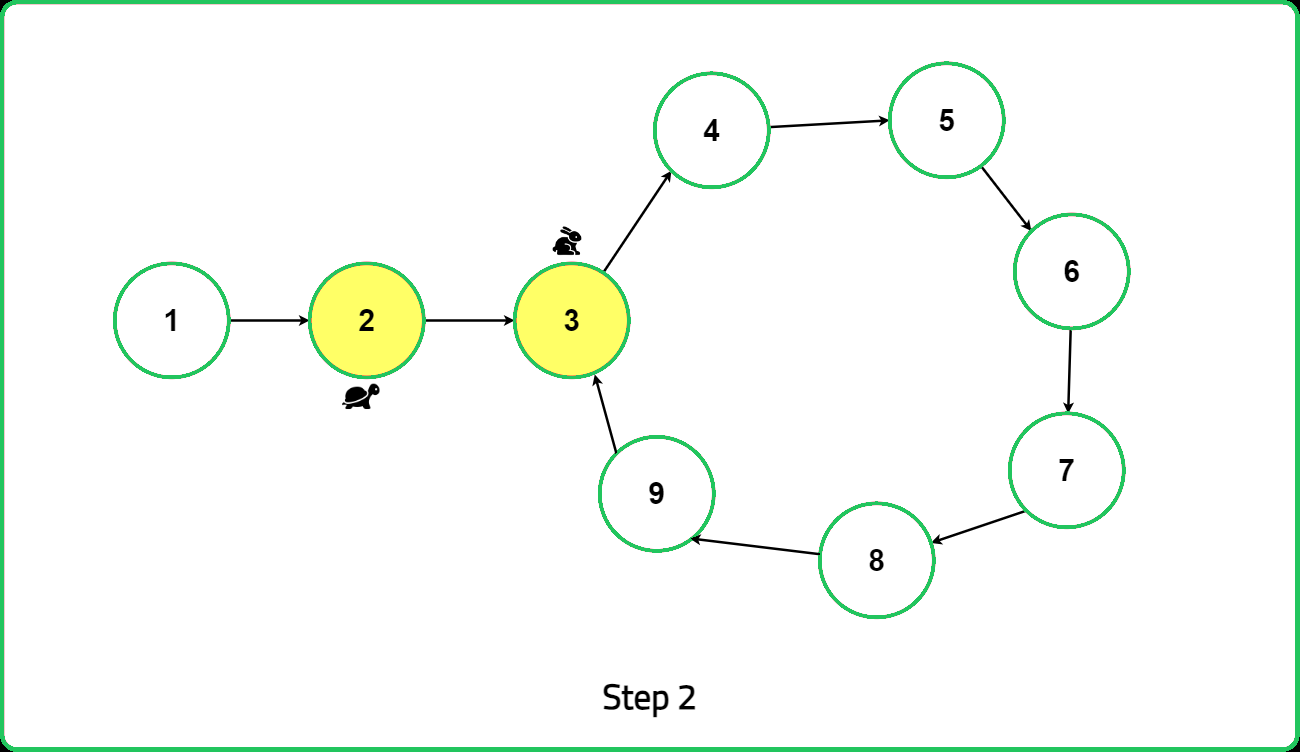
Initialize two pointers, slow and fast, to the head of the linked list. The slow pointer will advance one step at a time, while the fast pointer will advance two steps at a time. These pointers will move simultaneously through the list.
Traversal:
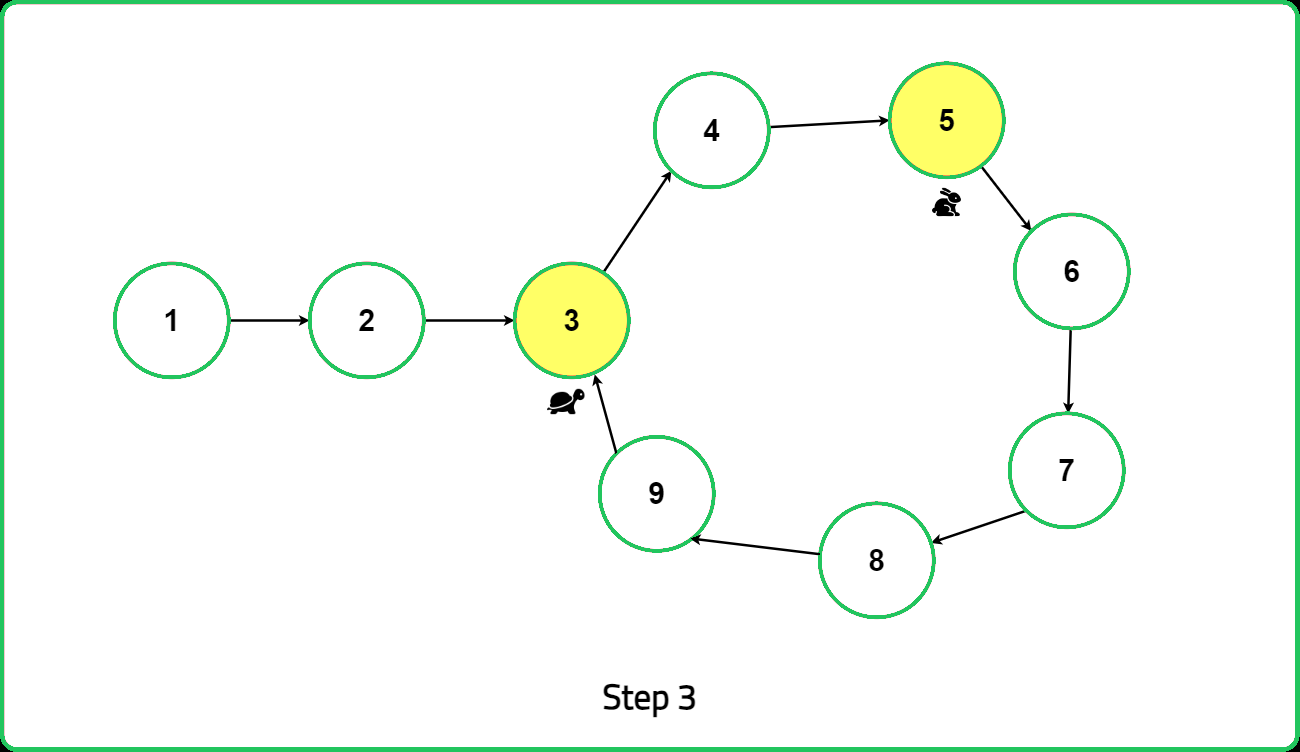
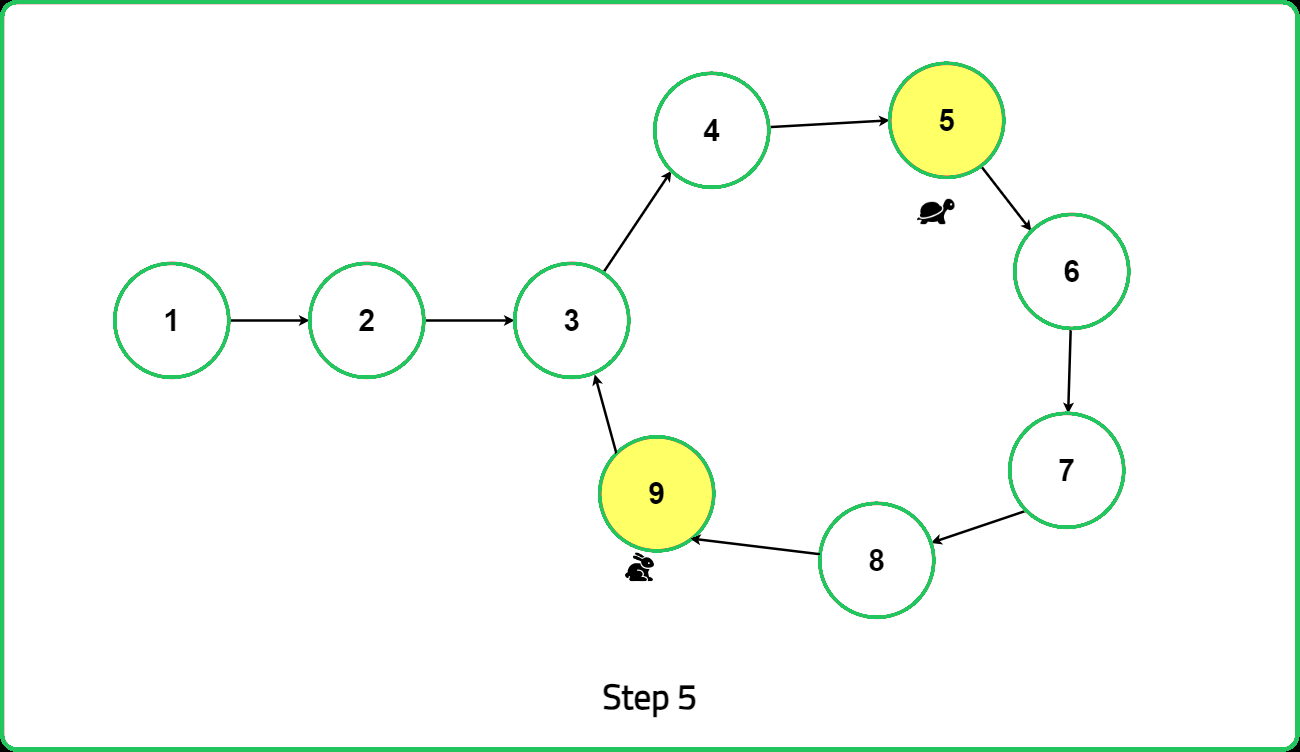
As the traversal progresses, move the slow pointer one step and the fast pointer two steps at a time. This continues until one of two conditions is met: if fast or fast.next reaches the end of the linked list (i.e., becomes null), it means there is no loop in the linked list, and the algorithm terminates by returning null. Alternatively, if the fast and slow pointers meet at the same node, it indicates the presence of a loop in the linked list.
Finding the Loop's Start:
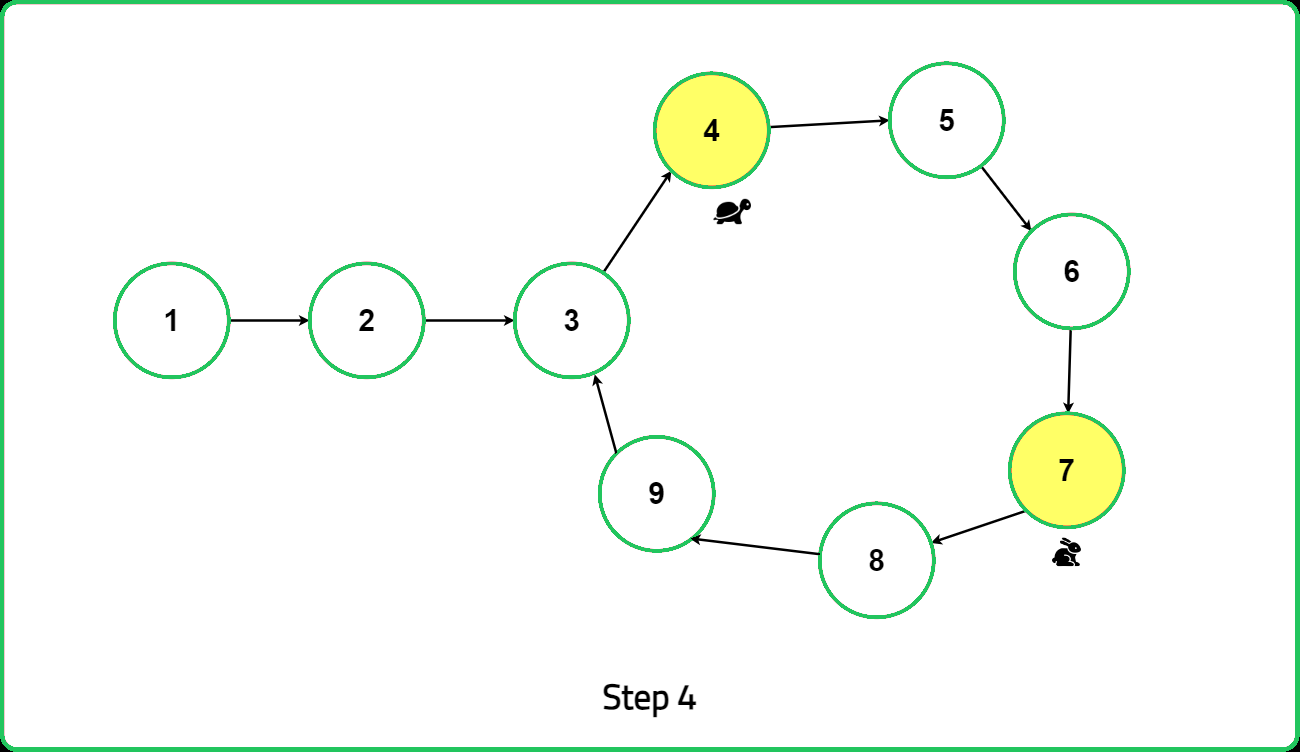
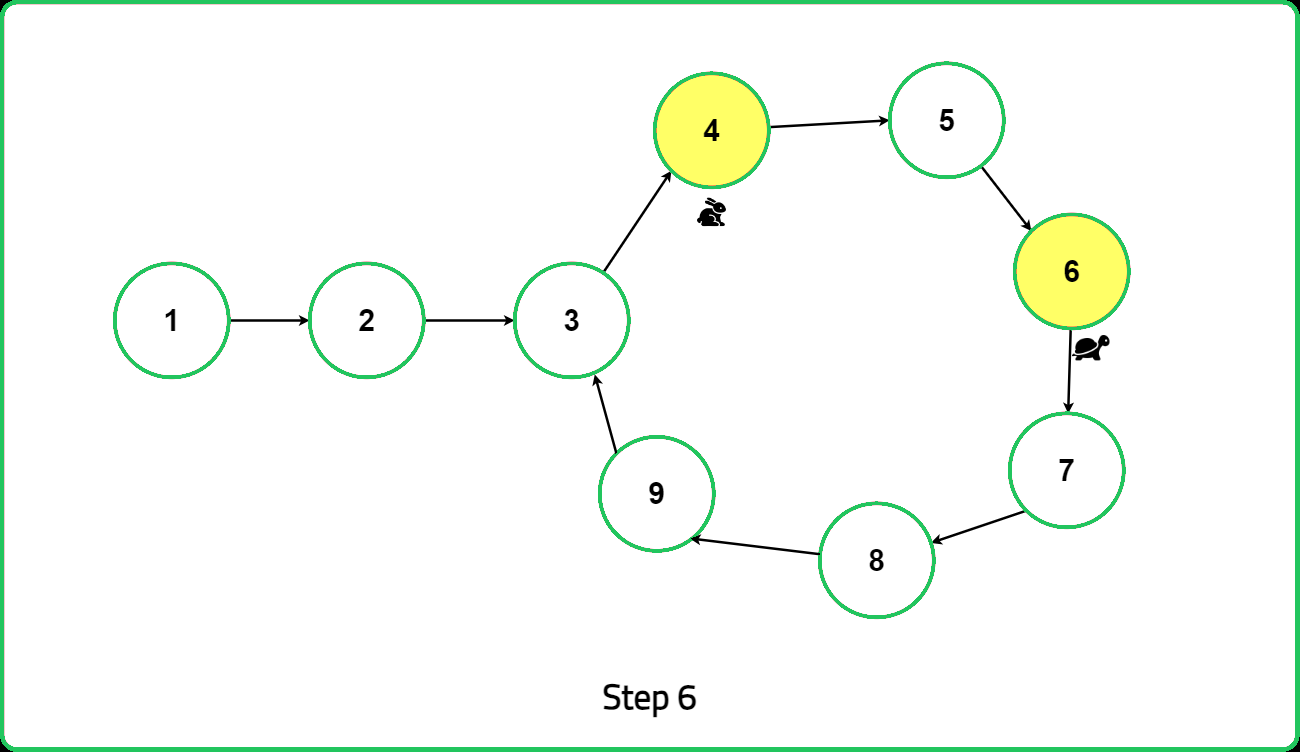
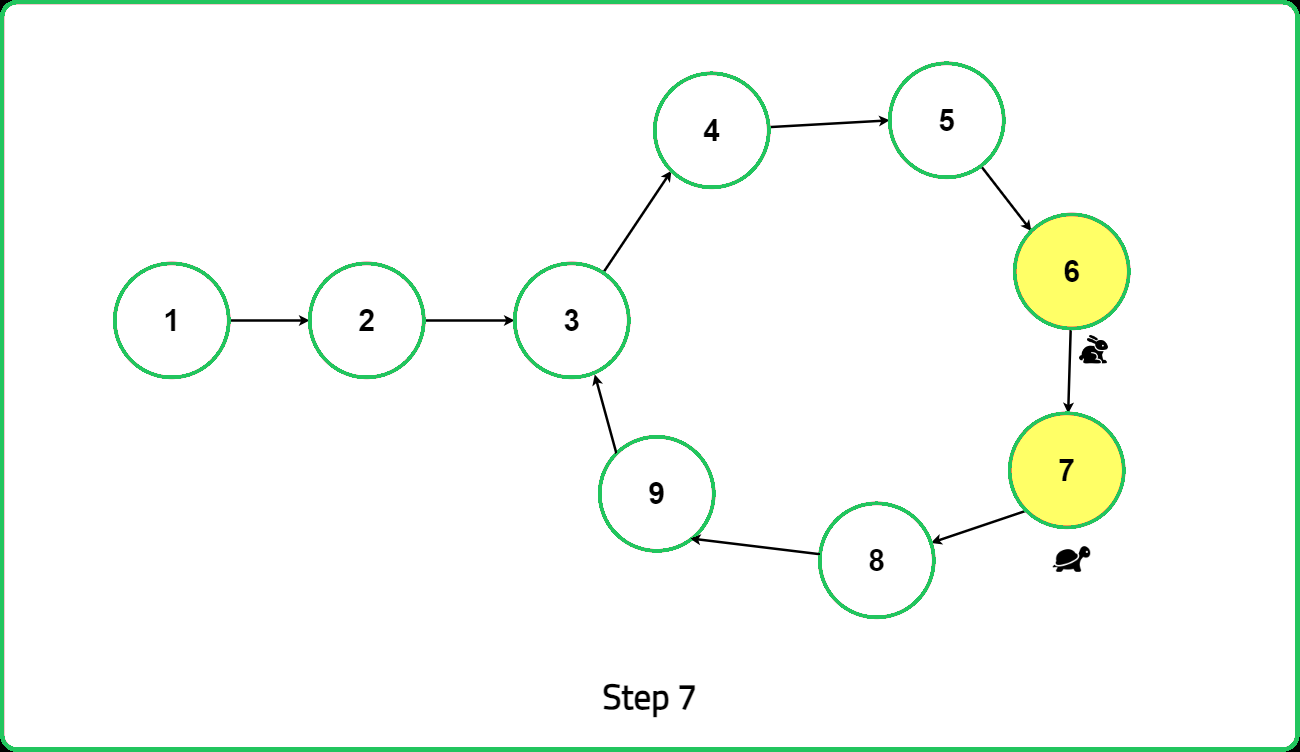
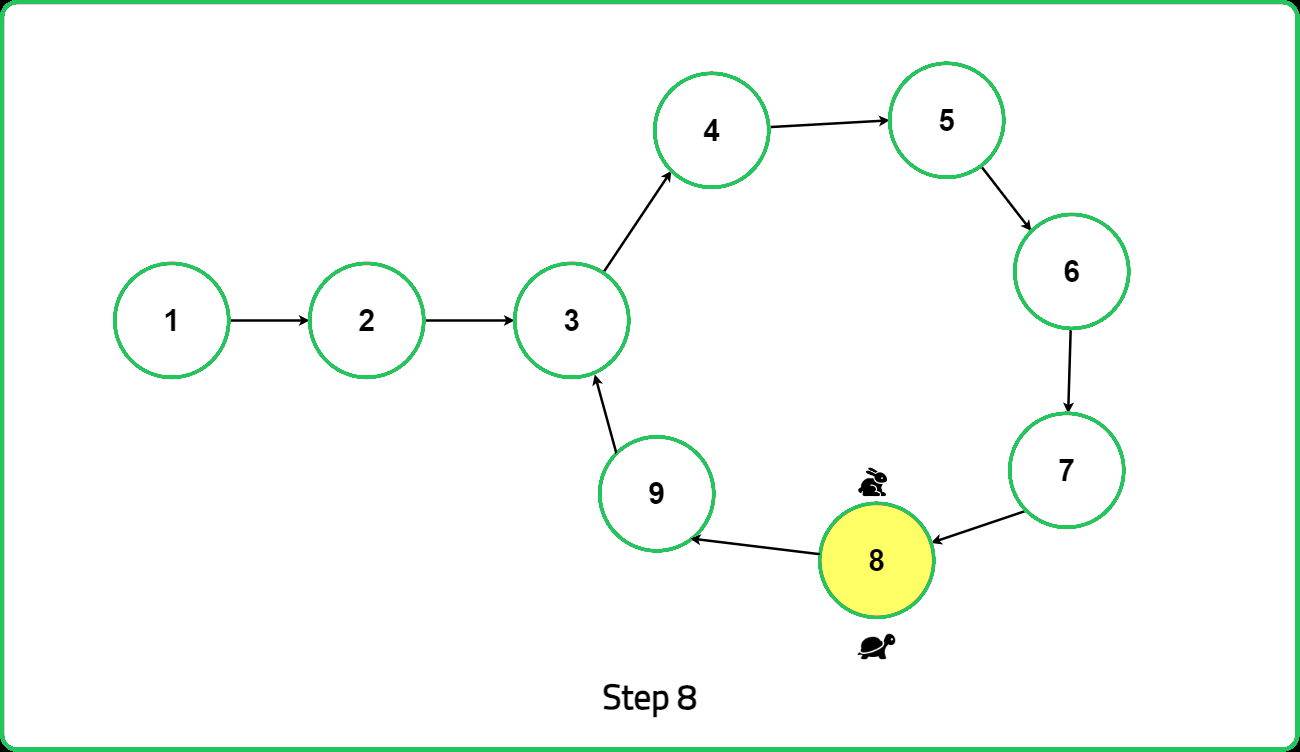
Once a loop is detected, reset the slow pointer to the head of the linked list. Then, move both the fast and slow pointers one step at a time. The point where they meet again is identified as the starting point of the loop. This method ensures efficient detection and pinpointing of the loop's starting location in the linked list.
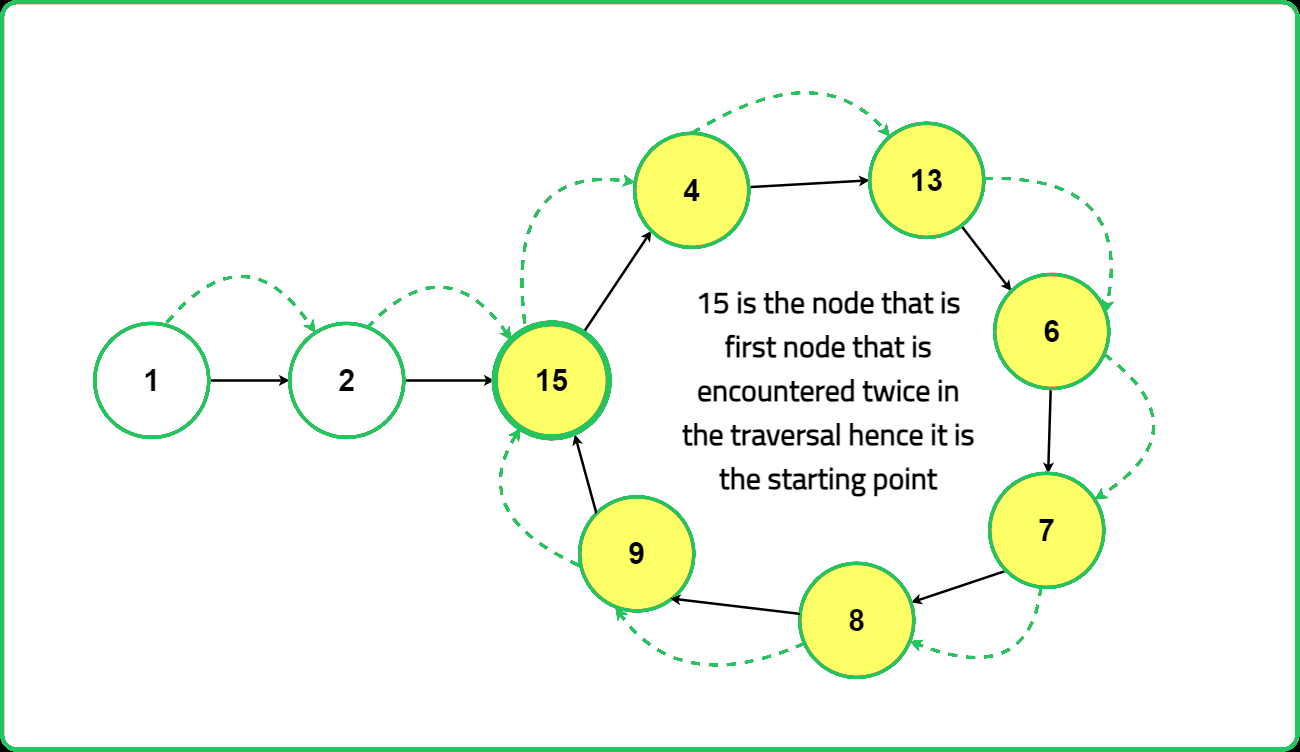
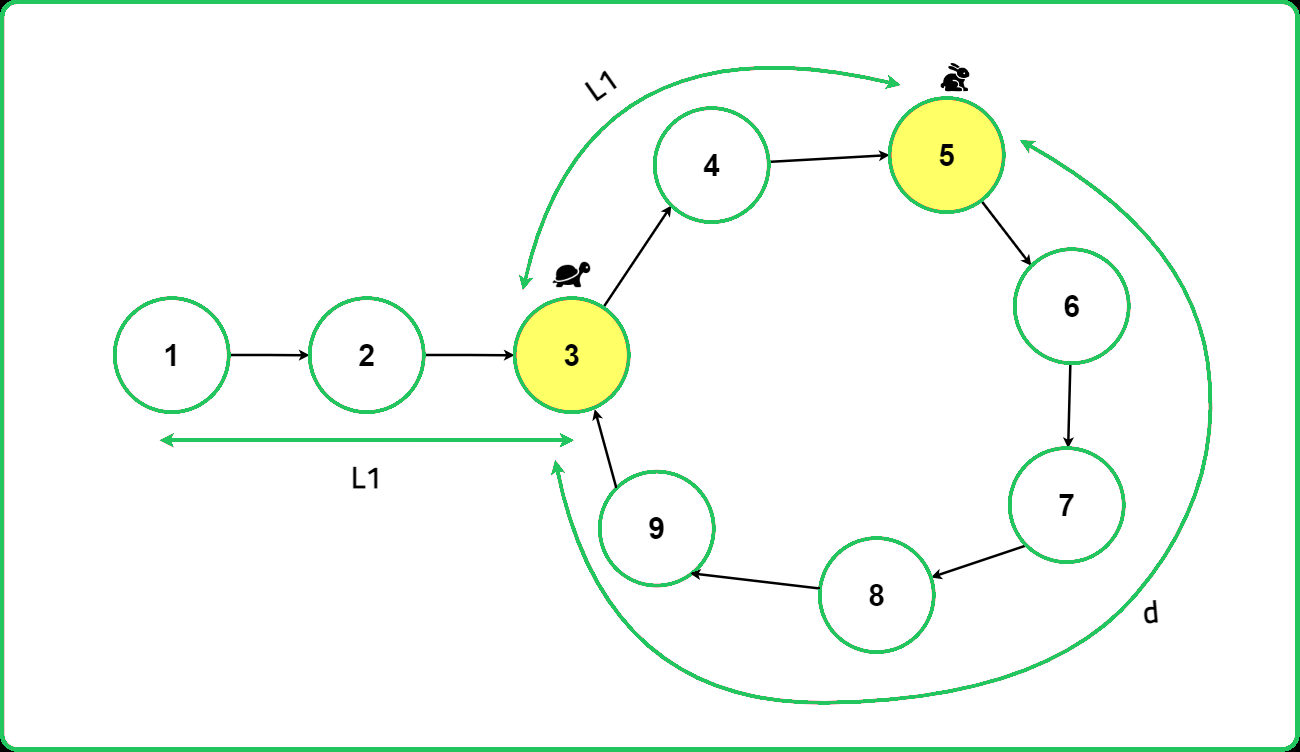
Proof of the Approach
You might wonder how this algorithm works, and it all comes down to the concept that the meeting point of the slow and fast pointers can be used to find the start of the loop.
In the "tortoise and hare" method for detecting loops in a linked list, when the slow pointer (tortoise) reaches the start of the loop, the fast pointer (hare) is at a position that is twice the distance traveled by the slow pointer. This happens because the hare moves twice as fast as the tortoise.
If the slow pointer has traveled a distance of L1, then the fast pointer has traveled 2 * L1. Now, both pointers are inside the loop, and the distance the fast pointer needs to cover to catch up with the slow pointer is the total length of the loop minus L1. Let's call this distance d.
- Distance traveled by slow = L1
- Distance traveled by fast = 2 * L1
- Total length of loop = L1 + d
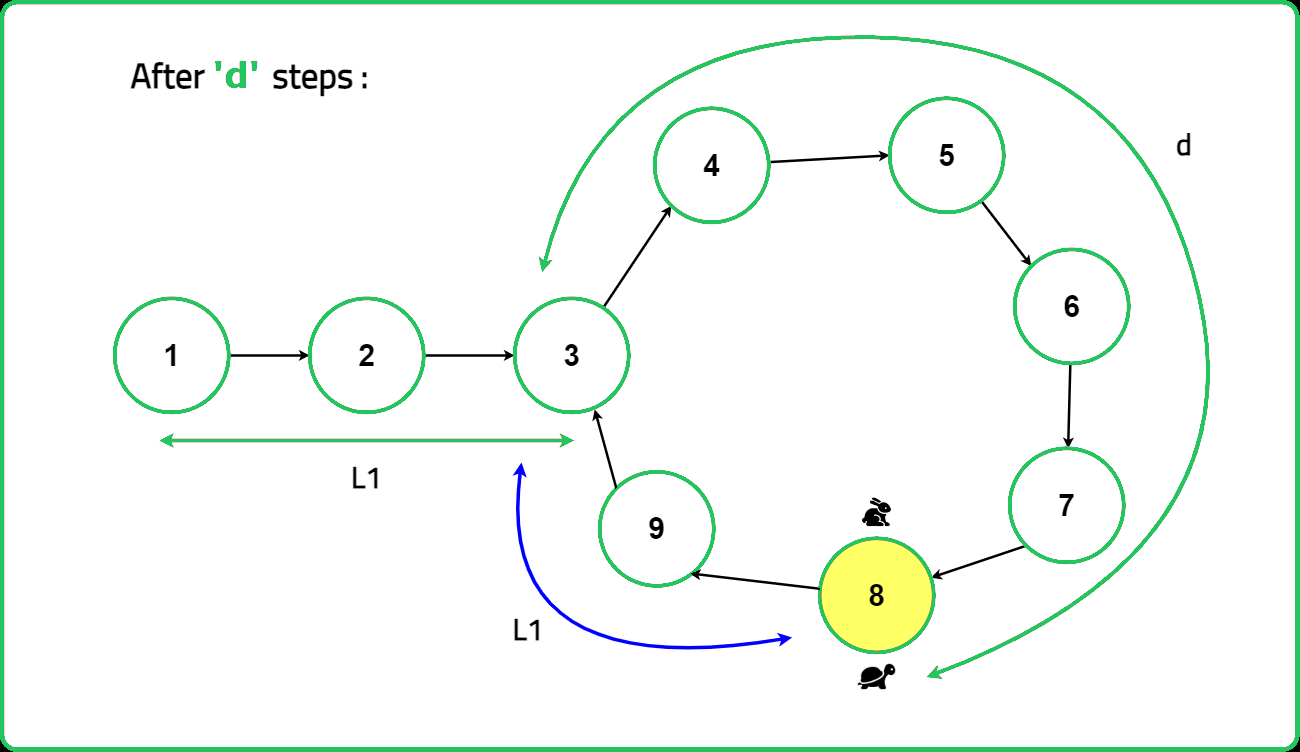
In this setup, the fast pointer moves two steps forward while the slow pointer moves one step forward in each iteration. This reduces the gap between them by one step each time. Given that the initial gap is d, it will take exactly d steps for the fast pointer to catch up with the slow pointer.
- Total length of loop = L1 + d
- Distance between slow and fast = d
During these d steps, the slow pointer will move d steps from the start of the loop, and the fast pointer will move 2 * d steps to meet the slow pointer. According to our calculations, the total length of the loop is L1 + d. Since the slow pointer covers a distance of d inside the loop, the remaining distance in the loop equals L1.
Thus, we can see that the distance from the start of the loop to the meeting point is equal to the distance from the start of the linked list to the start of the loop. This proves that the point where the two pointers meet is indeed the start of the loop in the linked list.
Dry Run
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117
#include <iostream>
using namespace std;
//Definition of singly linked list:
struct ListNode
{
int val;
ListNode *next;
ListNode()
{
val = 0;
next = NULL;
}
ListNode(int data1)
{
val = data1;
next = NULL;
}
ListNode(int data1, ListNode *next1)
{
val = data1;
next = next1;
}
};
class Solution {
public:
//Function to find the first node
//Of the loop in a linked list
ListNode* findStartingPoint(ListNode* head) {
//Initialize a slow and fast
//Pointers to the head of the list
ListNode* slow = head;
ListNode* fast = head;
// Phase 1: Detect the loop
while (fast != NULL && fast->next != NULL) {
// Move slow one step
slow = slow->next;
// Move fast two steps
fast = fast->next->next;
// If slow and fast meet,
// a loop is detected
if (slow == fast) {
// Reset the slow pointer
// To the head of the list
slow = head;
// Phase 2: Find the first node of the loop
while (slow != fast) {
// Move slow and fast one step
// At a time
slow = slow->next;
fast = fast->next;
// When slow and fast meet again,
// It's the first node of the loop
}
// Return the first node of the loop
return slow;
}
}
//If no loop is found,
//Return NULL
return NULL;
}
};
int main() {
// Create a sample linked list with a loop
ListNode* node1 = new ListNode(1);
ListNode* node2 = new ListNode(2);
node1->next = node2;
ListNode* node3 = new ListNode(3);
node2->next = node3;
ListNode* node4 = new ListNode(4);
node3->next = node4;
ListNode* node5 = new ListNode(5);
node4->next = node5;
// Make a loop from node5 to node2
node5->next = node2;
// Set the head of the linked list
ListNode* head = node1;
// Detect the loop in the linked list
Solution sol;
ListNode* loopStartNode = sol.findStartingPoint(head);
if (loopStartNode) {
cout << "Loop detected. Starting node of the loop is: " << loopStartNode->val << endl;
} else {
cout << "No loop detected in the linked list." << endl;
}
// Clean up memory (free the allocated nodes)
delete node1;
delete node2;
delete node3;
delete node4;
delete node5;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
//Definition of singly linked list:
class ListNode {
int val;
ListNode next;
ListNode() {
val = 0;
next = null;
}
ListNode(int data1) {
val = data1;
next = null;
}
ListNode(int data1, ListNode next1) {
val = data1;
next = next1;
}
}
class Solution {
public ListNode findStartingPoint(ListNode head) {
// Initialize a slow and fast
// pointers to the head of the list
ListNode slow = head;
ListNode fast = head;
// Phase 1: Detect the loop
while (fast != null && fast.next != null) {
// Move slow one step
slow = slow.next;
// Move fast two steps
fast = fast.next.next;
// If slow and fast meet,
// a loop is detected
if (slow == fast) {
// Reset the slow pointer
// to the head of the list
slow = head;
// Phase 2: Find the first node of the loop
while (slow != fast) {
// Move slow and fast one step
// at a time
slow = slow.next;
fast = fast.next;
// When slow and fast meet again,
// it's the first node of the loop
}
// Return the first node of the loop
return slow;
}
}
// If no loop is found, return null
return null;
}
}
public class Main {
public static void main(String[] args) {
// Create a sample linked list with a loop
ListNode node1 = new ListNode(1);
ListNode node2 = new ListNode(2);
node1.next = node2;
ListNode node3 = new ListNode(3);
node2.next = node3;
ListNode node4 = new ListNode(4);
node3.next = node4;
ListNode node5 = new ListNode(5);
node4.next = node5;
// Make a loop from node5 to node2
node5.next = node2;
// Set the head of the linked list
ListNode head = node1;
// Detect the loop in the linked list
Solution sol = new Solution();
ListNode loopStartNode = sol.findStartingPoint(head);
if (loopStartNode != null) {
System.out.println("Loop detected. Starting node of the loop is: " + loopStartNode.val);
} else {
System.out.println("No loop detected in the linked list.");
}
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
# Definition of singly linked list:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def findStartingPoint(self, head):
# Initialize a slow and fast
# pointers to the head of the list
slow = head
fast = head
# Phase 1: Detect the loop
while fast is not None and fast.next is not None:
# Move slow one step
slow = slow.next
# Move fast two steps
fast = fast.next.next
# If slow and fast meet,
# a loop is detected
if slow == fast:
# Reset the slow pointer
# to the head of the list
slow = head
# Phase 2: Find the first node of the loop
while slow != fast:
# Move slow and fast one step
# at a time
slow = slow.next
fast = fast.next
# When slow and fast meet again,
# it's the first node of the loop
return slow
# If no loop is found, return None
return None
# Function to create a sample linked list with a loop and detect the loop
if __name__ == "__main__":
# Create a sample linked list with a loop
node1 = ListNode(1)
node2 = ListNode(2)
node1.next = node2
node3 = ListNode(3)
node2.next = node3
node4 = ListNode(4)
node3.next = node4
node5 = ListNode(5)
node4.next = node5
# Make a loop from node5 to node2
node5.next = node2
# Set the head of the linked list
head = node1
# Detect the loop in the linked list
sol = Solution()
loop_start_node = sol.findStartingPoint(head)
if loop_start_node:
print(f"Loop detected. Starting node of the loop is: {loop_start_node.val}")
else:
print("No loop detected in the linked list.")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
//Definition of singly linked list:
class ListNode {
constructor(val = 0, next = null) {
this.val = val;
this.next = next;
}
}
class Solution {
findStartingPoint(head) {
// Initialize a slow and fast
// pointers to the head of the list
let slow = head;
let fast = head;
// Phase 1: Detect the loop
while (fast !== null && fast.next !== null) {
// Move slow one step
slow = slow.next;
// Move fast two steps
fast = fast.next.next;
// If slow and fast meet,
// a loop is detected
if (slow === fast) {
// Reset the slow pointer
// to the head of the list
slow = head;
// Phase 2: Find the first node of the loop
while (slow !== fast) {
// Move slow and fast one step
// at a time
slow = slow.next;
fast = fast.next;
// When slow and fast meet again,
// it's the first node of the loop
}
// Return the first node of the loop
return slow;
}
}
// If no loop is found, return null
return null;
}
}
// Function to create a sample linked list with a loop and detect the loop
function main() {
// Create a sample linked list with a loop
const node1 = new ListNode(1);
const node2 = new ListNode(2);
node1.next = node2;
const node3 = new ListNode(3);
node2.next = node3;
const node4 = new ListNode(4);
node3.next = node4;
const node5 = new ListNode(5);
node4.next = node5;
// Make a loop from node5 to node2
node5.next = node2;
// Set the head of the linked list
const head = node1;
// Detect the loop in the linked list
const sol = new Solution();
const loopStartNode = sol.findStartingPoint(head);
if (loopStartNode) {
console.log("Loop detected. Starting node of the loop is: " + loopStartNode.val);
} else {
console.log("No loop detected in the linked list.");
}
}
main();
Time Complexity: O(N) The code examines each node in the linked list exactly once, where 'N' is the total number of nodes. This results in a linear time complexity, O(N), as the traversal through the list is direct and sequential.
Space Complexity: O(1) The code uses a fixed amount of extra space, regardless of the size of the linked list. This is accomplished by employing two pointers, slow and fast, to detect the loop. Since no additional data structures are used that depend on the size of the list, the space complexity remains constant, O(1).