Morris Preorder Traversal

Binary Trees Traversal in Constant Space Hard

Given root of binary tree, return the preorder traversal of the binary tree.

Morris preorder Traversal is a tree traversal algorithm aiming to achieve a space complexity of O(1) without recursion or an external data structure.

Examples:

Input : root = [1, 4, null, 4 2]

Output : [1, 4, 4, 2]

Explanation :

Input : root = [1]

Output : [1]

Explanation : Only root node is present.

Input : root = [1, 4, 2, 9, null, null, 6]

Constraints

1 <= Number of Nodes <= 100
-100 Node.val <= 100

Hints

If a node has a left child, find its inorder predecessor (rightmost node in the left subtree). Create a temporary link from the inorder predecessor to the current node to allow backtracking. If a node has no left child, visit it directly and move right.
Print the node before moving to the left subtree (Preorder: Root → Left → Right). If revisiting via the threaded link, remove the link and move right.

Company Tags

PayPal McKinsey & Company Snowflake Western Digital Zynga Etsy Databricks Ernst & Young Salesforce Morgan Stanley HCL Technologies Lyft Epic Systems Qualcomm Walmart Red Hat Johnson & Johnson Wayfair Robinhood Stripe Roblox Reddit Medtronic KPMG Philips Healthcare Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition

To address this problem, it is crucial to understand the Morris Inorder Traversal technique for binary trees. Morris Inorder Traversal, known for its space efficiency, can be adapted to perform Preorder Traversal by modifying the traversal method. Specifically, in Preorder Morris Traversal, the value of the current node is printed before proceeding to its left child, but only if the right child of the inorder predecessor is null.

This modification maintains the core structure of Morris Traversal while ensuring that nodes are processed in the sequence required for Preorder Traversal. As a result, the traversal remains efficient, operating in constant space, as it does not require additional data structures.

Approach

Begin by initializing a pointer, current, to traverse the tree, and set it to the root node of the binary tree.
Perform the traversal while current is not null:
1. If the current node does not have a left child, print the value of the current node and move to its right child.
2. If the current node has a left child:
  1. Identify the inorder predecessor of the current node, which is the rightmost node in the left subtree.
  2. If the right child of this inorder predecessor is null, establish a temporary link by setting the right child of the inorder predecessor to the current node. Print the value of the current node and move to its left child.
  3. If the right child of the inorder predecessor is not null, this indicates that the temporary link established earlier has been encountered. Therefore, revert the changes by setting the right child of the inorder predecessor back to null and proceed to the current node’s right child.

Continue this process until the traversal reaches the end of the binary tree.

Dry Run

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int data;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    vector<int> preorder(TreeNode* root) {
        // Vector to store the preorder traversal result
        vector<int> preorder;
        // Pointer to the current node, starting with the root
        TreeNode* cur = root;

        /* 
        Iterate until the current node becomes null
        If the current node has no left child
        Add the value of the current node to the preorder list
        */
        while (cur != NULL) {
            if (cur->left == NULL) {
                preorder.push_back(cur->data);
                cur = cur->right;
            } 
        /* 
        If the current node has a left child create a pointer 
        to traverse to the rightmost node in the left subtree
        or until we find a node whose right child is not yet processed
        */     
            else {
                TreeNode* prev = cur->left;
                while (prev->right && prev->right != cur) {
                    prev = prev->right;
                }
        /* 
        If the right child of the rightmost node is null 
        set the right child of the rightmost node to the current node
        Add the value of the current node to the preorder list
        and move to the left child
        */        

                if (prev->right == NULL) {
                    prev->right = cur;
                    preorder.push_back(cur->data);
                    cur = cur->left;
                } 

        /* If the right child of the rightmost node is not null
        Reset the right child to null and move to the right child */ 

                else {
                    prev->right = NULL;
                    cur = cur->right;
                }
            }
        }
        // Return the resulting preorder traversal list
        return preorder;
    }
};

int main() {
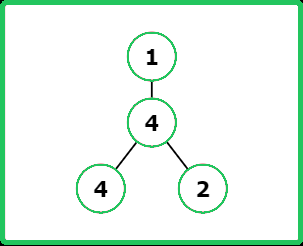
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(4);
    root->left->left = new TreeNode(4);
    root->left->left->left = new TreeNode(2);

    Solution sol;
    vector<int> preorder = sol.preorder(root);

    cout << "Binary Tree Morris Preorder Traversal: ";
    for (int i : preorder) {
        cout << i << " ";
    }
    cout << endl;

    return 0;
}
// Definition for a binary tree node.
  public class TreeNode {
      int data;
      TreeNode left;
      TreeNode right;
      TreeNode(int val) { data = val; left = null, right = null; }
  }


class Solution {
    public List<Integer> preorder(TreeNode root) {
        // List to store the preorder traversal result
        List<Integer> preorder = new ArrayList<>();
        
        // Pointer to the current node, starting with the root
        TreeNode cur = root;
        
        /* 
        Iterate until the current node becomes null
        If the current node has no left child
        Add the value of the current node to the preorder list
        */

        while (cur != null) {
            if (cur.left == null) {
                preorder.add(cur.data);
                cur = cur.right;
            } else {

        /* 
        If the current node has a left child create a pointer 
        to traverse to the rightmost node in the left subtree
        or until we find a node whose right child is not yet processed
        */  

            TreeNode prev = cur.left;   
            while (prev.right != null && prev.right != cur) {
                    prev = prev.right;
            }

        /* 
        If the right child of the rightmost node is null 
        set the right child of the rightmost node to the current node
        Add the value of the current node to the preorder list
        and move to the left child
        */
            if (prev.right == null) {
                    prev.right = cur;
                    preorder.add(cur.data);
                    cur = cur.left;
                } 
               
        /*
        If the right child of the rightmost node is not null
        Reset the right child to null and move to the right child 
        */   
            else {
                prev.right = null;
                cur = cur.right;
                }
            }
        }
        
        // Return the resulting preorder traversal list
        return preorder;
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(4);
        root.left.left = new TreeNode(4);
        root.left.left.left = new TreeNode(2);

        Solution sol = new Solution();
        List<Integer> preorder = sol.preorder(root);

        System.out.println("Binary Tree Morris Preorder Traversal: " + preorder);
    }
}
# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.data = val
        self.left = left
        self.right = right

class Solution:
    def preorder(self, root):
        # List to store the preorder traversal result
        preorder = []
        
        # Pointer to the current node, starting with the root
        cur = root
        
        # Iterate until the current node becomes None
        while cur:
            # If the current node has no left child
            # Add the value of the current node to the preorder list
            if not cur.left:
                preorder.append(cur.data)
                # Move to the right child
                cur = cur.right
            else:
            # If the current node has a left child
            # Create a pointer to traverse to the rightmost node in the left subtree
                prev = cur.left
                
            # Traverse to the rightmost node in the left subtree
            # or until we find a node whose right child is not yet processed
                while prev.right and prev.right != cur:
                    prev = prev.right
                
            # If the right child of the rightmost node is null
            # Set the right child of the rightmost node to the current node
            # Add the value of the current node to the preorder list and
            # move to the left child

                if not prev.right:
                    prev.right = cur
                    preorder.append(cur.data)
                    cur = cur.left

            # If the right child of the rightmost node is not null
            # Reset the right child to null
                else:
                    prev.right = None
                    cur = cur.right
        
        # Return the resulting preorder traversal list
        return preorder

# Example usage:
root = TreeNode(1)
root.left = TreeNode(4)
root.left.left = TreeNode(4)
root.left.left.left = TreeNode(2)

sol = Solution()
preorder = sol.preorder(root)
print("Binary Tree Morris Preorder Traversal: ", preorder)
//Definition for a binary tree node.
  class TreeNode {
       constructor(val = 0, left = null, right = null){
           this.data = val;
           this.left = left;
           this.right = right;
       }
  }

class Solution {
    preorder(root) {
        // List to store the preorder traversal result
        const preorder = [];
        
        // Pointer to the current node, starting with the root
        let cur = root;
        
        /* 
        Iterate until the current node becomes null
        If the current node has no left child
        Add the value of the current node to the preorder list
        */

        while (cur !== null) {
            if (cur.left === null) {
                preorder.push(cur.data);
                cur = cur.right;
            } else {

        /* 
        If the current node has a left child create a pointer 
        to traverse to the rightmost node in the left subtree
        or until we find a node whose right child is not yet processed
        */
                let prev = cur.left;
                while (prev.right !== null && prev.right !== cur) {
                    prev = prev.right;
                }
                
        /* 
        If the right child of the rightmost node is null 
        set the right child of the rightmost node to the current node
        Add the value of the current node to the preorder list
        and move to the left child
        */
                if (prev.right === null) {
                    prev.right = cur;
                    preorder.push(cur.data);
                    cur = cur.left;
                } else {

        /*
        If the right child of the rightmost node is not null
        Reset the right child to null and move to the right child 
       */
                    prev.right = null;                   
                    cur = cur.right;
                }
            }
        }
        
        // Return the resulting preorder traversal list
        return preorder;
    }
}

// Example usage:
const root = new TreeNode(1);
root.left = new TreeNode(4);
root.left.left = new TreeNode(4);
root.left.left.left = new TreeNode(2);

const sol = new Solution();
const preorder = sol.preorder(root);

Complexity Analysis

Time Complexity: O(2N) where N is the number of nodes in the Binary Tree. The algorithm visits each node at most twice.

Space Complexity: O(1) The algorithm uses constant extra space for auxiliary variables.

Code

Problem List