Top View of BT

Binary Trees FAQs Medium

Fun Fact: The underlying concept of this problem, which is traversing through a binary tree, is extensively used in databases as well as file systems
For instance, the B-tree structure, a type of binary tree, allows for efficient insertion, deletion and search operations
This is especially beneficial for databases and file systems where data is large and needs to be stored on the hard drive
In cases like these, reducing the number of disk access during operations is crucial for the overall performance
So, understanding how to traverse binary trees isn't just restricted to coding puzzles, but has very tangible real-world applications in software development!

Given the root of a binary tree, return the top view of the binary tree.

Top view of a binary tree is the set of nodes visible when the tree is viewed from the top. Return nodes from the leftmost node to the rightmost node. Also if 2 nodes are outside the shadow of the tree and are at the same position then consider the left ones only(i.e. leftmost).

Examples:

Input : root = [1, 2, 3, 4, 5, 6, 7]

Output : [4, 2, 1, 3, 7]

Explanation :

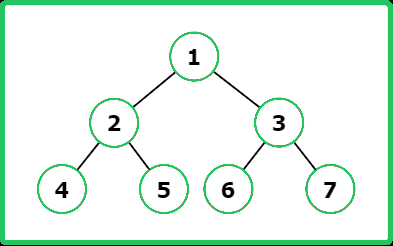
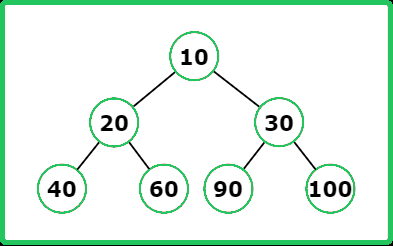
Input : root = [10, 20, 30, 40, 60, 90, 100]

Output : [40, 20, 10, 30, 100]

Explanation :

Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]

Constraints

1 <= Number of Nodes <= 10⁴
-10³<= Node.val <= 10³

Hints

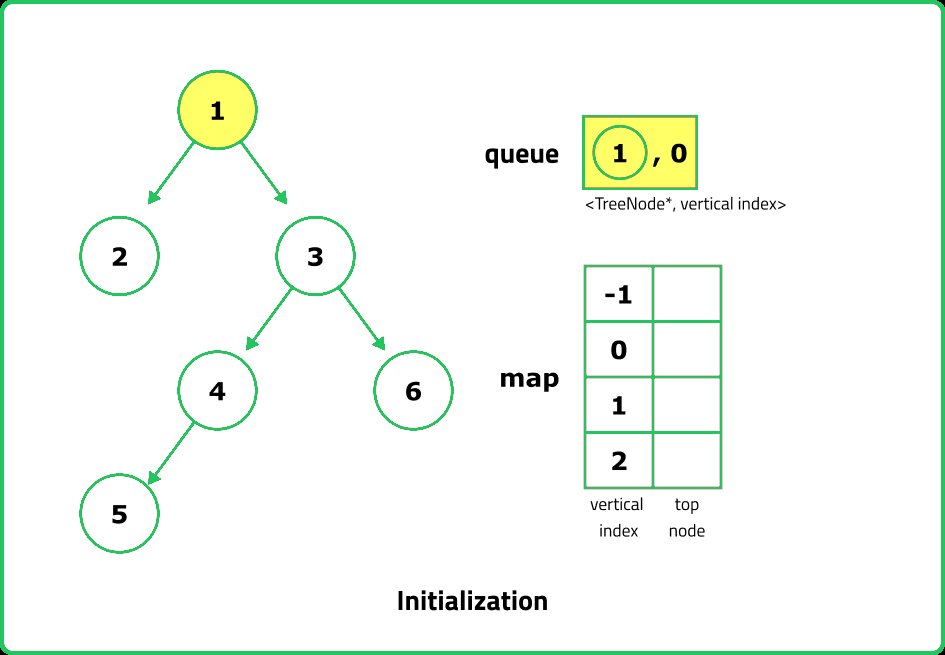
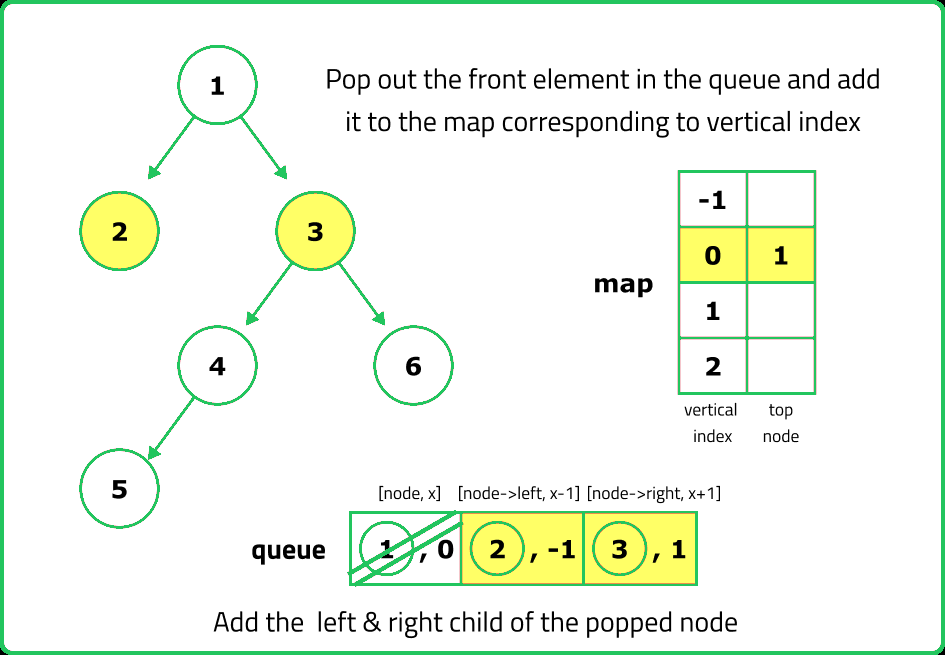
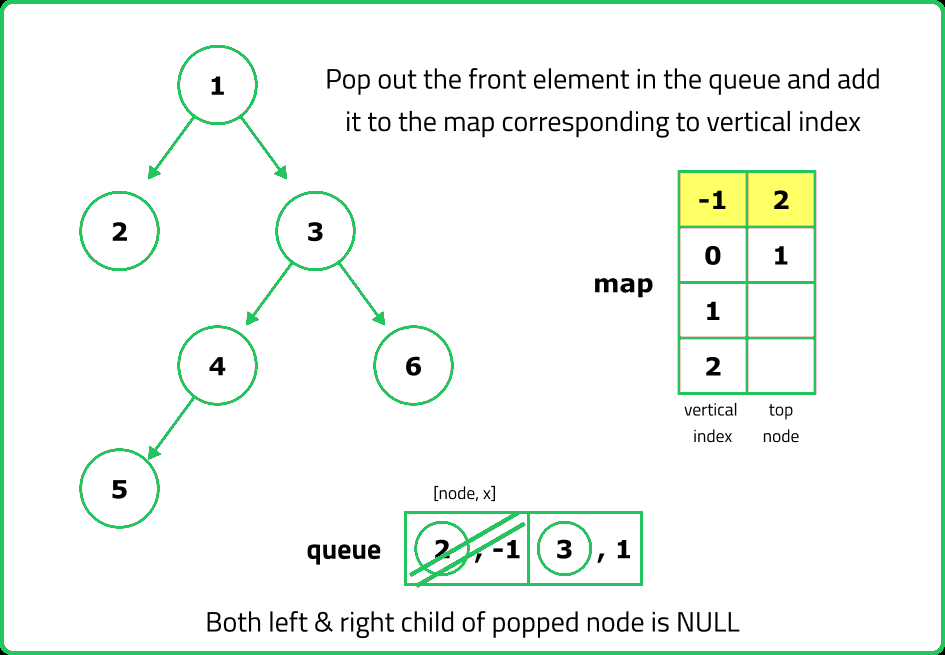
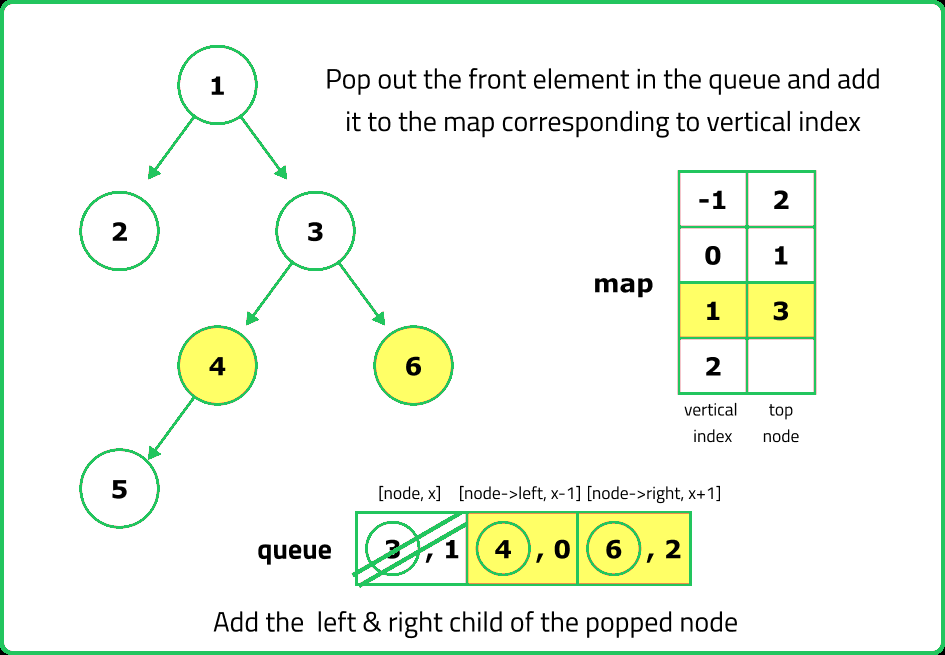
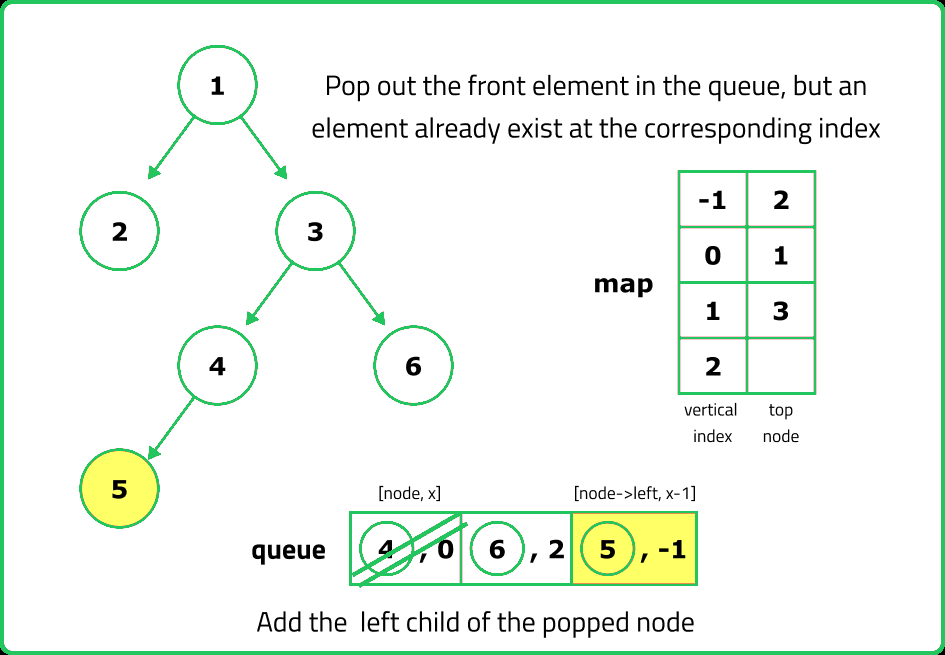
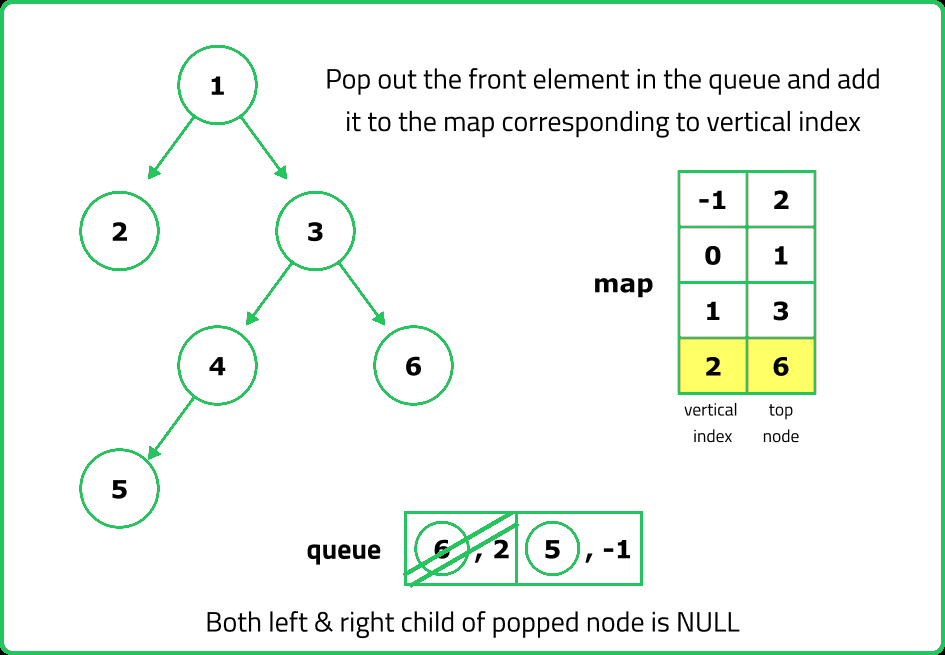
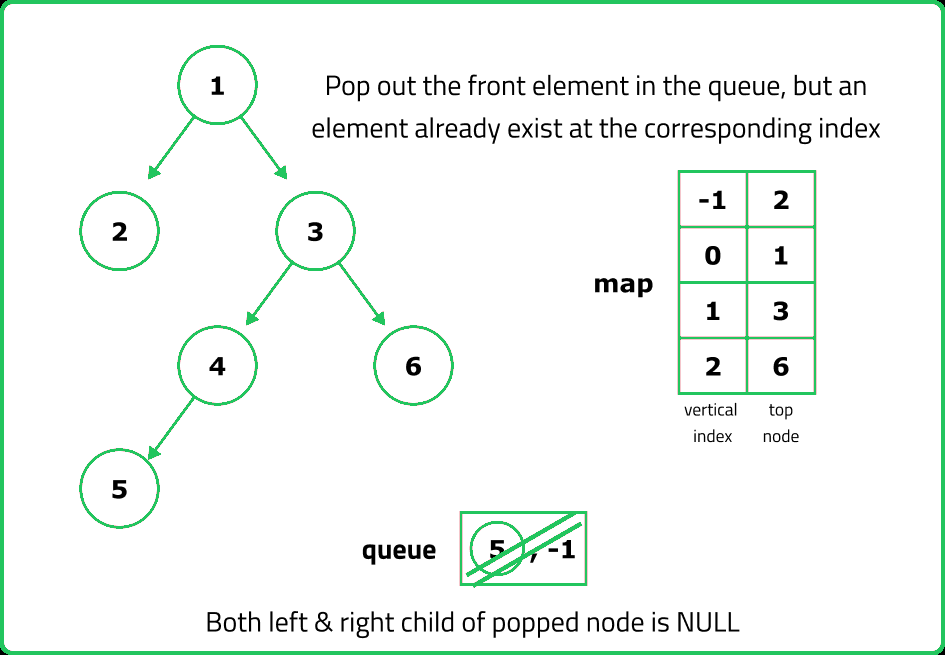
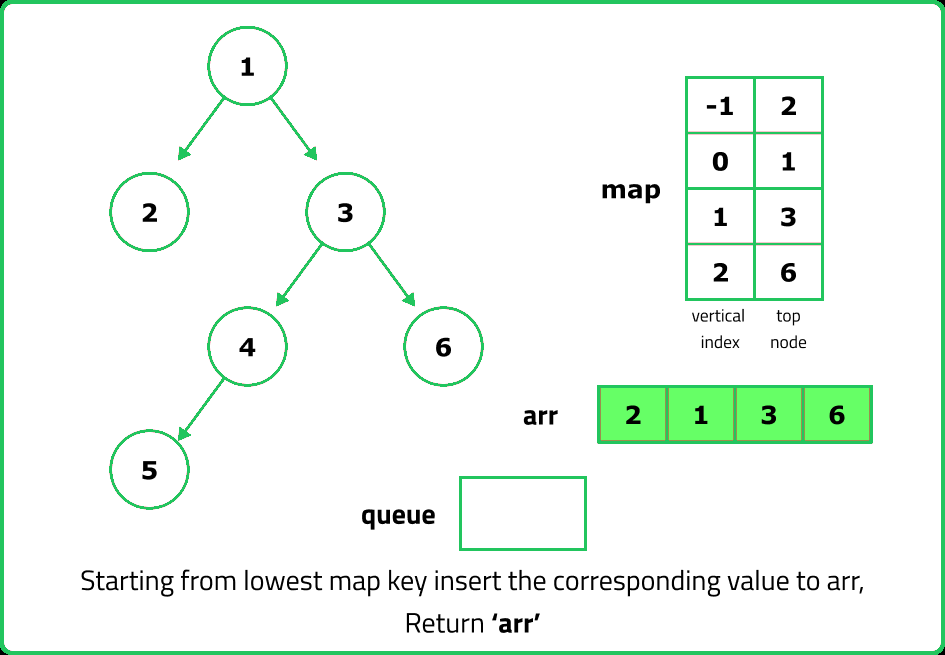
Use a queue of tuples (node, horizontal_distance), starting with (root, 0). Process each node level by level, ensuring that we encounter nodes in top-to-bottom order.
Use a hashmap (top_nodes) where: Key: Horizontal Distance (HD). Value: First node encountered at that HD. If an HD is encountered for the first time, store the node’s value.

Company Tags

AMD NVIDIA Splunk Zomato Medtronic Twilio Instacart Unity Technologies Zoho Pinterest Flipkart Epic Games IBM Cloudflare eBay Seagate Technology Zynga Bloomberg Freshworks Riot Games Optum JPMorgan Chase Red Hat Reddit OYO Rooms Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition

The top view of a binary tree can be visualized by imagining vertical lines passing through the tree. Each vertical line represents a unique vertical position, with nodes to the right having positive indexes and nodes to the left having negative indexes. To find the top view, we need the nodes that are first encountered from each vertical position as we traverse the tree horizontally.

Approach

Initialize a vector named ans to hold the final result of the top view traversal. Also, set up a map to store nodes based on their vertical positions, using the vertical index as the key and the node's value as the associated data.
Set up a queue to facilitate breadth-first search (BFS) traversal, starting with the root node, which is assigned a vertical position of 0.
Perform the following steps while the queue is not empty:
- Dequeue the node at the front of the queue and retrieve its vertical position. If this vertical position is not yet present in the map, add the node’s value to the map. This signifies that the node is the first one encountered at this vertical position and should be included in the top view.
- If the vertical position is already in the map, skip adding this node, as a node positioned higher in the tree at this vertical coordinate has already been processed and thus represents the top view for that vertical line.
- Enqueue the left child of the current node with a vertical position decremented by 1 (current position - 1) and the right child with a vertical position incremented by 1 (current position + 1).
After completing the BFS traversal, iterate through the map to gather nodes in ascending order of their vertical positions. Append these nodes to the ans vector. Finally, return the ans vector, which represents the top view traversal of the binary tree.

Dry Run

Solution

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node
struct TreeNode {
    int data;
    TreeNode *left;
    TreeNode *right;
    // Constructor to initialize the node with a value
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    // Function to return the top view of the binary tree
    vector<int> topView(TreeNode *root) {
        // Vector to store the result
        vector<int> ans;
        
        // Check if the tree is empty
        if (root == nullptr) {
            return ans;
        }
        
        // Map to store the top view nodes based on their vertical positions
        map<int, int> mpp;
        
        // Queue for BFS traversal, each element is a pair containing node and its vertical position
        queue<pair<TreeNode*, int>> q;
        
        // Push the root node with its vertical position (0) into the queue
        q.push({root, 0});
        
        // BFS traversal
        while (!q.empty()) {
            // Retrieve the node and its vertical position from the front of the queue
            auto it = q.front();
            q.pop();
            TreeNode *node = it.first;
            int line = it.second;
            
            // If the vertical position is not already in the map, add the node's data to the map
            if (mpp.find(line) == mpp.end()) {
                mpp[line] = node->data;
            }
            
            // Process left child
            if (node->left != nullptr) {
                // Push the left child with a decreased vertical position into the queue
                q.push({node->left, line - 1});
            }
            
            // Process right child
            if (node->right != nullptr) {
                // Push the right child with an increased vertical position into the queue
                q.push({node->right, line + 1});
            }
        }
        
        // Transfer values from the map to the result vector
        for (auto it : mpp) {
            ans.push_back(it.second);
        }
        
        return ans;
    }
};

int main() {
    // Creating a sample binary tree
    TreeNode *root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(10);
    root->left->left->right = new TreeNode(5);
    root->left->left->right->right = new TreeNode(6);
    root->right = new TreeNode(3);
    root->right->right = new TreeNode(10);
    root->right->left = new TreeNode(9);

    Solution solution;

    // Get the top view traversal
    vector<int> topView = solution.topView(root);

    // Print the result
    cout << "Top View Traversal: " << endl;
    for (auto node : topView) {
        cout << node << " ";
    }

    return 0;
}
import java.util.*;

class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        data = val;
        left = null;
        right = null;
    }
}

class Solution {
    // Nested generic Pair class
    static class Pair<  K , V  > {
        private K key;
        private V value;

        public Pair(K key, V value) {
            this.key = key;
            this.value = value;
        }

        public K getKey() {
            return key;
        }

        public V getValue() {
            return value;
        }
    }

    // Function to return the top view of the binary tree
    public List< Integer > topView(TreeNode root) {
        // List to store the result
        List< Integer > ans = new ArrayList<>();

        // Check if the tree is empty
        if (root == null) {
            return ans;
        }

        // Map to store the top view nodes based on their vertical positions
        Map< Integer, Integer > mpp = new TreeMap<>();

        // Queue for BFS traversal, each element is a pair containing node and its vertical position
        Queue< Pair < TreeNode ,  Integer > > q = new LinkedList<>();

        // Push the root node with its vertical position (0) into the queue
        q.add(new Pair<>(root, 0));

        // BFS traversal
        while (!q.isEmpty()) {
            // Retrieve the node and its vertical position from the front of the queue
            Pair< TreeNode, Integer > it = q.poll();
            TreeNode node = it.getKey();
            int line = it.getValue();

            // If the vertical position is not already in the map, add the node's data to the map
            if (!mpp.containsKey(line)) {
                mpp.put(line, node.data);
            }

            // Process left child
            if (node.left != null) {
                // Push the left child with a decreased vertical position into the queue
                q.add(new Pair<>(node.left, line - 1));
            }

            // Process right child
            if (node.right != null) {
                // Push the right child with an increased vertical position into the queue
                q.add(new Pair<>(node.right, line + 1));
            }
        }

        // Transfer values from the map to the result list
        for (Integer value : mpp.values()) {
            ans.add(value);
        }

        return ans;
    }
}

public class Main {
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);
        root.right.left = new TreeNode(6);
        root.right.right = new TreeNode(7);

        Solution solution = new Solution();
        List result = solution.topView(root);

        System.out.println("Top View: " + result);
    }
}
from collections import deque

# Definition for a binary tree node
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.data = val
        self.left = left
        self.right = right

class Solution:
    # Function to return the top view of the binary tree
    def topView(self, root):
        # List to store the result
        ans = []
        
        # Check if the tree is empty
        if root is None:
            return ans
        
        # Dictionary to store the top view nodes based on their vertical positions
        mpp = {}
        
        # Queue for BFS traversal, each element is a pair containing node and its vertical position
        q = deque([(root, 0)])
        
        # BFS traversal
        while q:
            # Retrieve the node and its vertical position from the front of the queue
            node, line = q.popleft()
            
            # If the vertical position is not already in the map, add the node's data to the map
            if line not in mpp:
                mpp[line] = node.data
            
            # Process left child
            if node.left:
                # Push the left child with a decreased vertical position into the queue
                q.append((node.left, line - 1))
            
            # Process right child
            if node.right:
                # Push the right child with an increased vertical position into the queue
                q.append((node.right, line + 1))
        
        # Transfer values from the map to the result list
        for key in sorted(mpp.keys()):
            ans.append(mpp[key])
        
        return ans

# Creating a sample binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.left.left = TreeNode(4)
root.left.right = TreeNode(10)
root.left.left.right = TreeNode(5)
root.left.left.right.right = TreeNode(6)
root.right = TreeNode(3)
root.right.right = TreeNode(10)
root.right.left = TreeNode(9)

solution = Solution()

# Get the top view traversal
top_view = solution.topView(root)

# Print the result
print("Top View Traversal:")
for node in top_view:
    print(node, end=" ")
// Definition for a binary tree node
class TreeNode {
    constructor(val = 0, left = null, right = null) {
        this.data = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    // Function to return the top view of the binary tree
    topView(root) {
        // Array to store the result
        const ans = [];
        
        // Check if the tree is empty
        if (root === null) {
            return ans;
        }
        
        // Map to store the top view nodes based on their vertical positions
        const mpp = new Map();
        
        // Queue for BFS traversal, each element is a pair containing node and its vertical position
        const q = [{ node: root, line: 0 }];
        
        // BFS traversal
        while (q.length > 0) {
            // Retrieve the node and its vertical position from the front of the queue
            const { node, line } = q.shift();
            
            // If the vertical position is not already in the map, add the node's data to the map
            if (!mpp.has(line)) {
                mpp.set(line, node.data);
            }
            
            // Process left child
            if (node.left !== null) {
                // Push the left child with a decreased vertical position into the queue
                q.push({ node: node.left, line: line - 1 });
            }
            
            // Process right child
            if (node.right !== null) {
                // Push the right child with an increased vertical position into the queue
                q.push({ node: node.right, line: line + 1 });
            }
        }
        
        // Transfer values from the map to the result array
        Array.from(mpp.keys()).sort((a, b) => a - b).forEach(key => {
            ans.push(mpp.get(key));
        });
        
        return ans;
    }
}

// Creating a sample binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(10);
root.left.left.right = new TreeNode(5);
root.left.left.right.right = new TreeNode(6);
root.right = new TreeNode(3);
root.right.right = new TreeNode(10);
root.right.left = new TreeNode(9);

const solution = new Solution();

// Get the top view traversal
const topView = solution.topView(root);

// Print the result
console.log("Top View Traversal:");
console.log(topView.join(" "));

Complexity Analysis

Time Complexity: O(N*logN), where N is the number of nodes in the Binary Tree.
This complexity arises because the algorithm performs a Breadth-First Search (BFS) traversal of the tree, visiting each node exactly once. And during the traversal, various map operations are performed which take logK complexity where K can be N in the worst case. Thus, the overall time complexity comes out to be O(N*logN).

Space Complexity: O(N) : The space complexity of the algorithm is O(N), where N is the number of nodes in the Binary Tree. This space is primarily consumed by the queue used for BFS traversal, which can hold up to N/2 nodes in the worst case scenario of a balanced tree. Additionally, a map is used to store nodes based on their vertical positions, potentially also using up to N/2 entries in the worst case. Therefore, the overall space usage is proportional to the maximum width of the tree at any level.

Code

Problem List