Floor and Ceil in a BST
Binary Search Trees
Theory and Basics
Easy
- This problem's underlying concept is extensively used in database management systems (DBMS) and indexing techniques
- For instance, when you're performing a database query using SQL to find a specific value in a table, a database system may use a binary search tree or B-tree internally (as an index) to look for that value
- This greatly reduces search time, especially in substantial-sized databases
- Finding floor and ceil values can be relevant in range-based queries or searches, such as identifying items in a certain price range on an e-commerce platform
- Hence, proficiency in understanding and solving such problems may contribute to optimizing database operations and queries
Given a root of binary search tree and a key(node) value, find the floor and ceil value for that particular key value.
- Floor Value Node: Node with the greatest data lesser than or equal to the key value.
- Ceil Value Node: Node with the smallest data larger than or equal to the key value.
If a particular floor or ceil value is not present then output -1.
Examples:
Input : root = [8, 4, 12, 2, 6, 10, 14] , key = 11
Output : [10, 12]
Explanation :
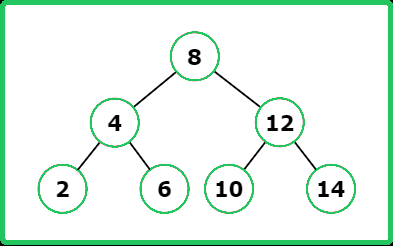
Input : root = [8, 4, 12, 2, 6, 10, 14] , key = 15
Output : [14, -1]
Explanation :
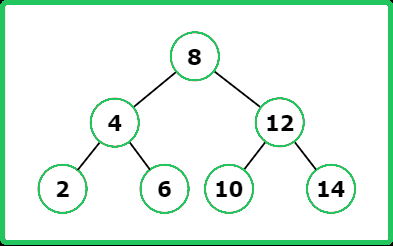
Input : root = [8, 4, 12, 2, 6, 10, 14] , key = 1
Constraints
- 1 <= Number of Nodes <= 5000
- 1 <= Node.val <= 107
- 1 <= key <= 107
Hints
- "Traverse the BST while updating floor and ceil. If key == root.val, Floor = key, Ceil = key (since key exists in BST). If key < root.val, Update ceil = root.val and Move left. If key > root.val, Update floor = root.val and Move right."
- "Recursively explore the BST based on key, updating floor and ceil dynamically. The base case occurs when we reach a null node."
Company Tags
Square
MongoDB
Roche
Broadcom
IBM
Epic Games
Lyft
Intel
Shopify
Unity Technologies
McKinsey & Company
Alibaba
Wayfair
DoorDash
Morgan Stanley
Salesforce
OYO Rooms
Reddit
Ernst & Young
Medtronic
Rakuten
Oracle
Swiggy
HCL Technologies
Red Hat
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe