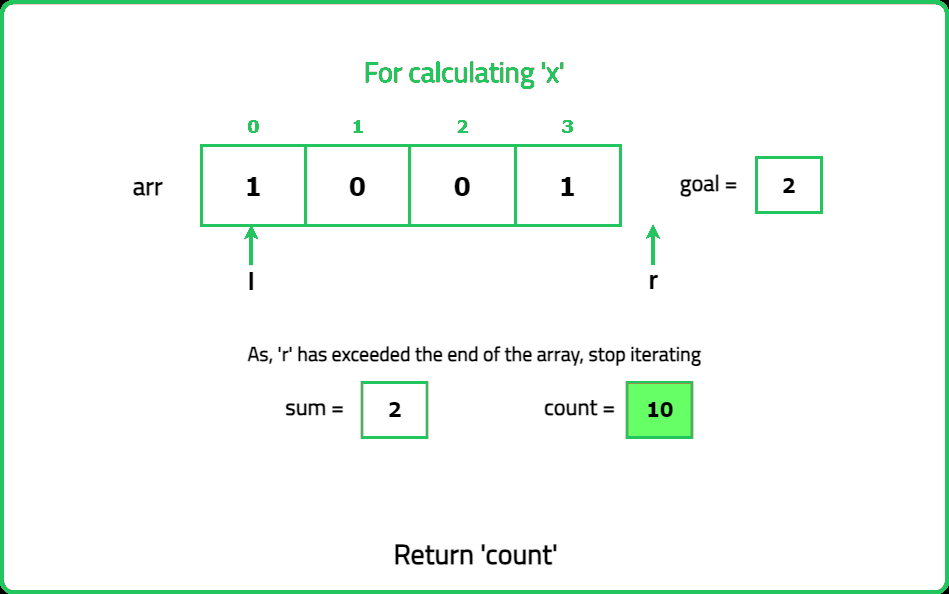
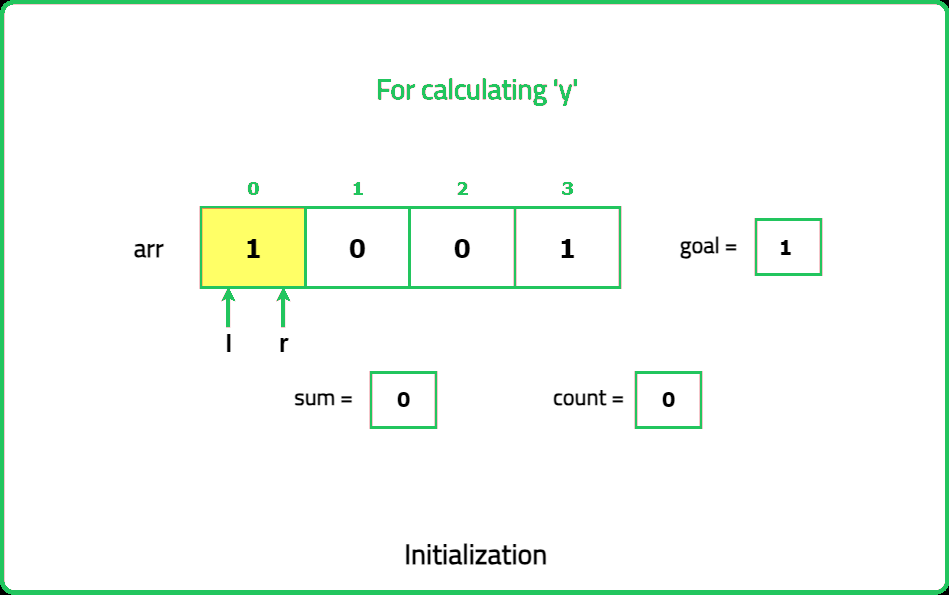
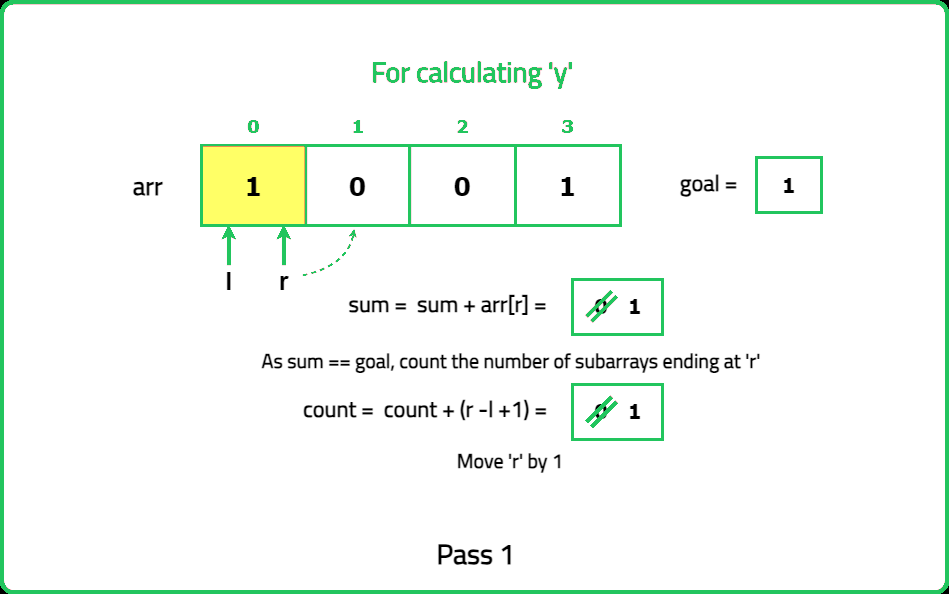
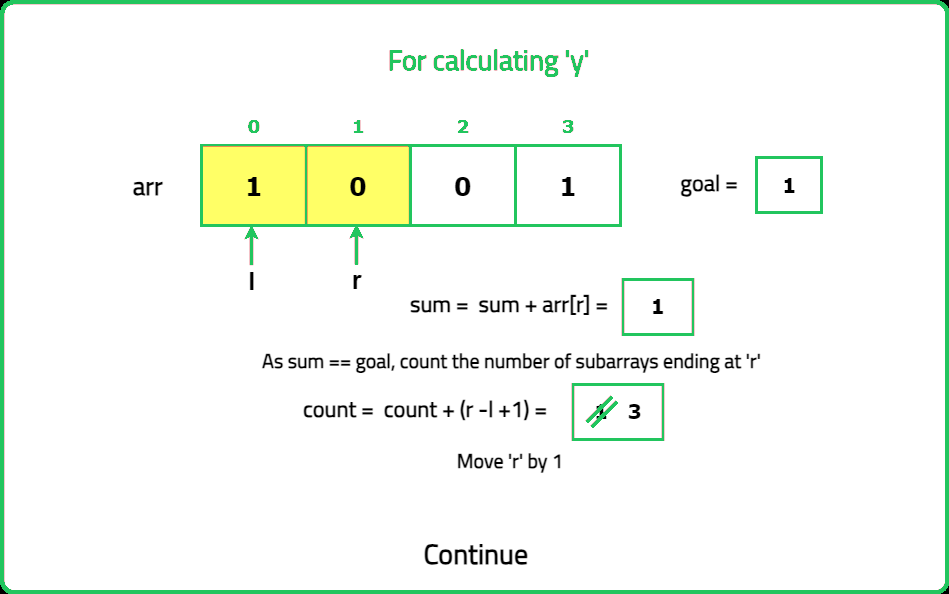
Binary Subarrays With Sum

Sliding Window / 2 Pointer Counting Subarrays / Substrings Problems Hard

This programming problem utilizes the concept of subarray sum computations, which are widely used in real-world applications such as image processing, where contiguous blocks of pixels need to be processed or manipulated
The concept is also used in data analysis applications where sequential data chunks need to be analyzed for a specified sum, like in financial software for calculating running totals in account statements
As an example, it is used in the implementation of features like "balance within last X transactions"

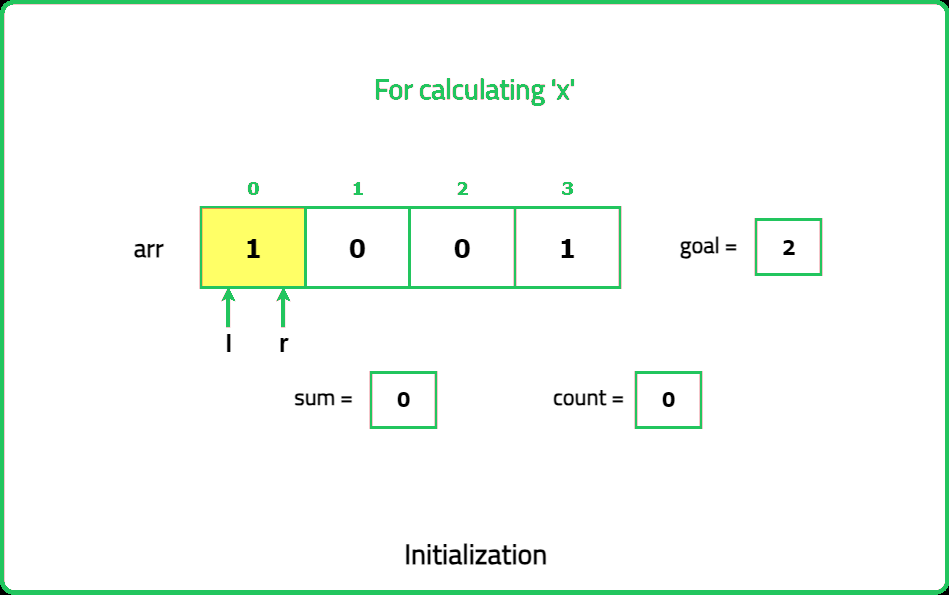
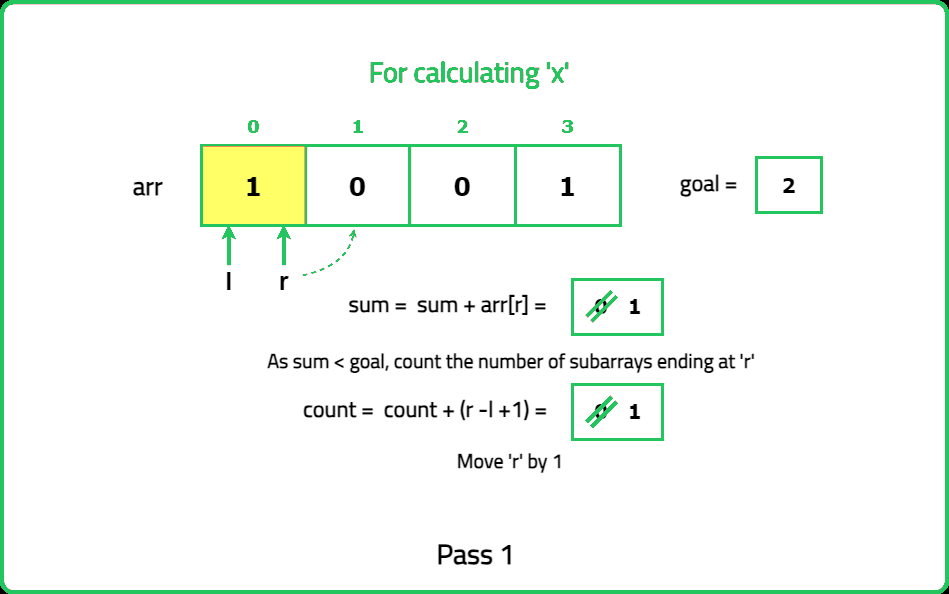
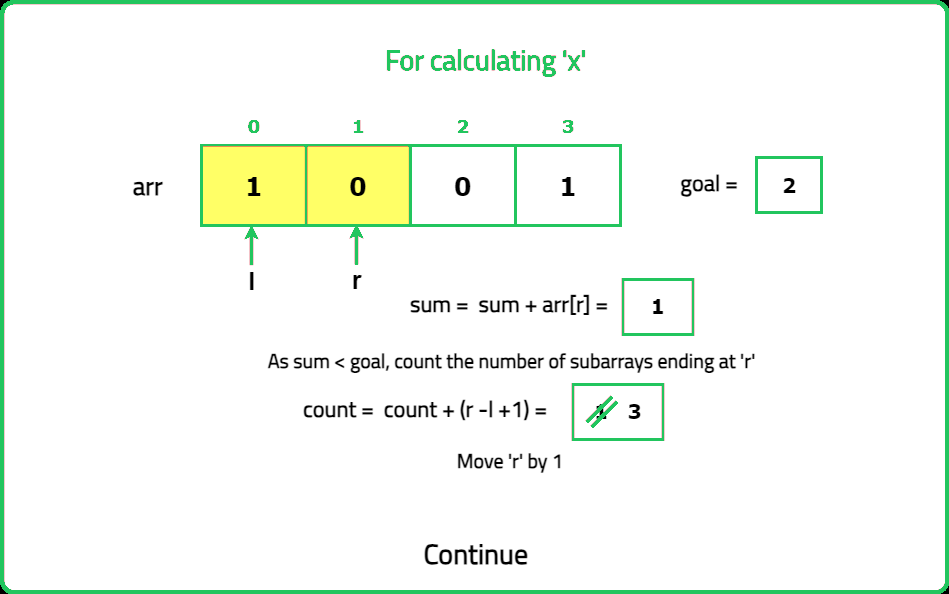
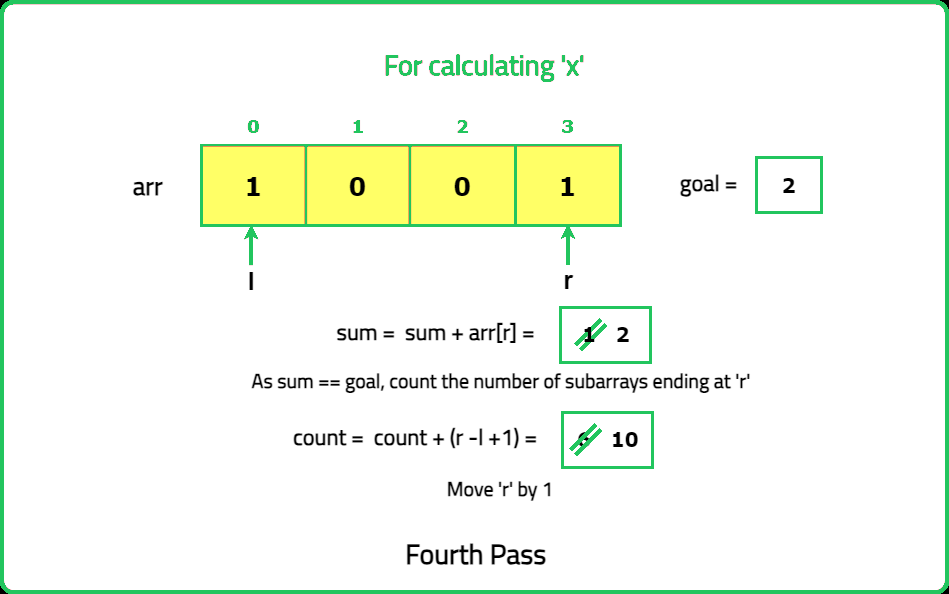
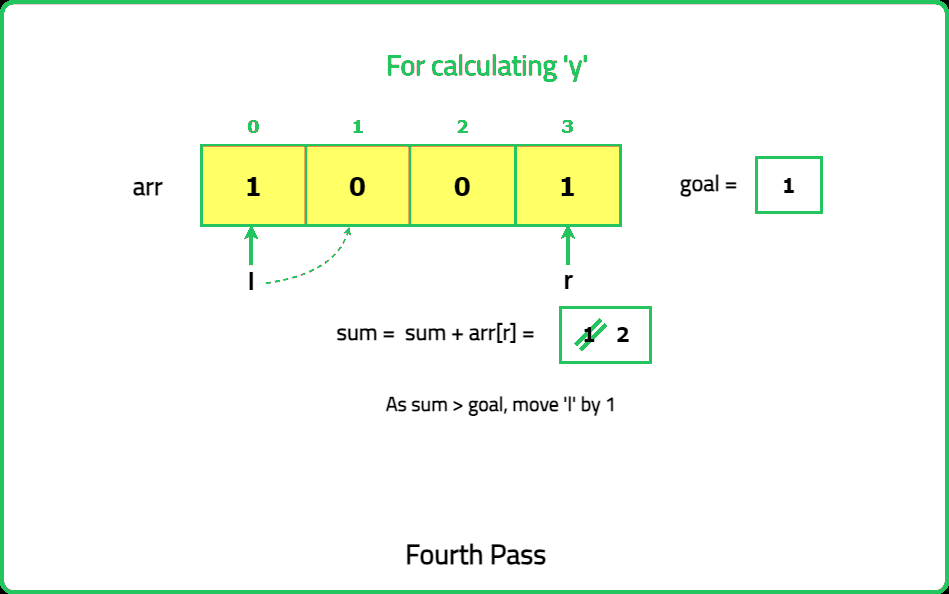
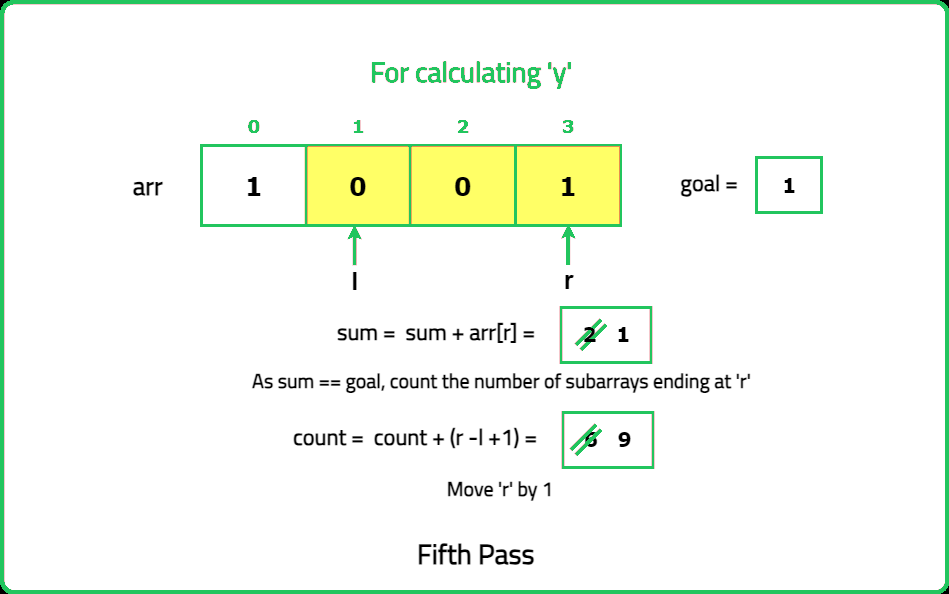
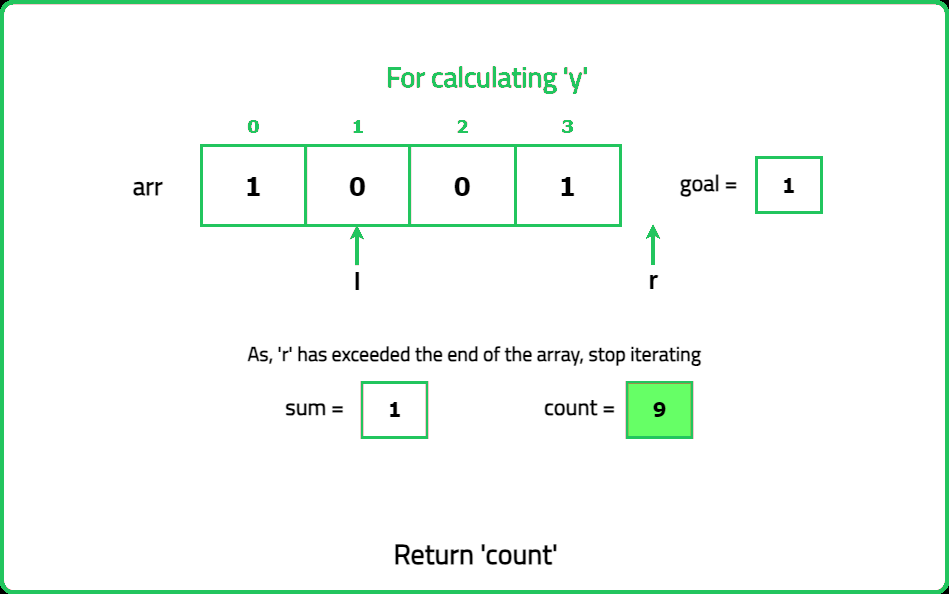
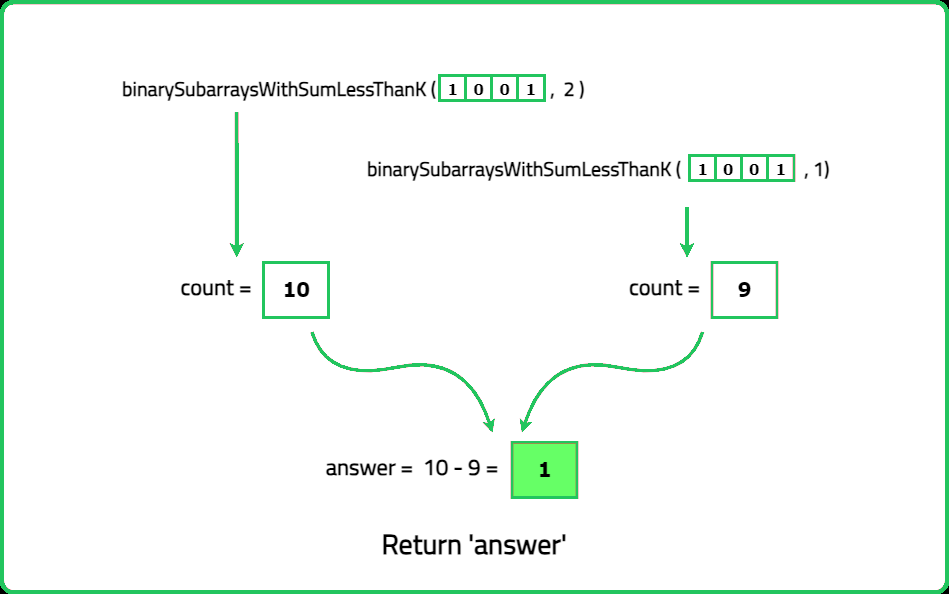
Given a binary array nums and an integer goal. Return the number of non-empty subarrays with a sum goal.

A subarray is a continuous part of the array.

Constraints

1 <= nums.length <= 3*10⁴
0 <= goal <= nums.length
nums consist of only 0 and 1.

Hints

Use a prefix sum to keep track of the cumulative sum up to each index. Store the count of each prefix sum in a hash map to efficiently determine how many subarrays with a sum equal to the goal exist.
For a subarray sum to equal the goal, the relationship current_sum−goal=prefix_sum must hold. Use the hash map to check how many times prefix_sum has occurred so far. Add that count to the result.

Company Tags

Stripe Nutanix Lyft Chewy Red Hat Roblox OYO Rooms Flipkart Siemens Healthineers Cerner Splunk Morgan Stanley Shopify Robinhood ARM Bain & Company Zoho AMD Deloitte McKinsey & Company HCL Technologies Databricks Target JPMorgan Chase Epic Games Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition:

Here, the idea is to use two-pointers approach to optimize the solution. So, basically instead of finding the count of substrings which have sum exactly equal to goal, try to find out count of subarrays whose sum is less than or equal to goal and the count of subarrays whose sum is less than or equal to goal-1. The difference of both the counts will provide the required result in linear time.

Approach:

Main Function:

It call the helper function to find out number of subarrays with sum less than or equal to goal.

In the second call, it gets the number of subarrays with sum less than or equal to goal - 1. Finally, the difference gives the exact count of subarrays with sum equal to goal.

Helper Function:

First, check for the edge case, if goal is negative, immediately return 0 because no valid subarray can have a negative sum.

Now, initialize few variables: l(left) and r (right) to mark the current window of subarrays within nums, sum to zero to track the current sum of elements in the window, count to zero to accumulate the number of valid subarrays.

Iterate through the array using the right pointer r. Add the element at right pointer to sum to include the current element in the window. While the sum is greater than goal decrease the sum and move the left pointer forward to shrink the window.

Then, Count all subarrays ending at r pointer that satisfy the sum condition. Move the right pointer forward and iterate the whole array. Finally, return count as an answer.

Dry-run :

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find the number of 
    subarrays with sum equal to `goal`*/
    int numSubarraysWithSum(vector<int>& nums, int goal) {
        
        /*Calculate the number of subarrays with 
        sum exactly equal to `goal` by using the 
        difference between subarrays with sum less
        than or equal to `goal` and those with sum
        less than or equal to `goal-1`*/
        return numSubarraysWithSumLessEqualToGoal(nums, goal) - numSubarraysWithSumLessEqualToGoal(nums, goal - 1);
    }
    
private:
    /* Helper function to find the number of 
    subarrays with sum less than or equal to `goal`*/
    int numSubarraysWithSumLessEqualToGoal(vector<int>& nums, int goal) {
        
        /* If goal is negative, there 
        can't be any valid subarray sum*/
        if (goal < 0) return 0;
        
        //Pointers to maintain the current window
        int l = 0, r = 0; 
        
        /* Variable to track the current 
        sum of elements in the window*/
        int sum = 0;      
        
        // Variable to count the number of subarrays
        int count = 0;   
        
        /* Iterate through the array 
        using the right pointer `r`*/
        while (r < nums.size()) {
            sum += nums[r]; 
            
            /* Shrink the window from the left
            side if the sum exceeds `goal`*/
            while (sum > goal) {
                sum -= nums[l];  
                
                // Move the left pointer `l` forward
                l++;            
            }
            
            /* Count all subarrays ending at
            `r` that satisfy the sum condition*/
            count += (r - l + 1);
            
            // Move the right pointer `r` forward 
            r++; 
        }
        
        // Return the total count of subarrays
        return count;
    }
};

int main() {
    vector<int> nums = {1, 0, 0, 1, 1, 0};
    int goal = 2;
    
    // Create an instance of Solution class
    Solution sol;
    
    int ans = sol.numSubarraysWithSum(nums, goal);

    // Print the result
    cout << "Number of substrings with sum \"" << goal << "\" is: " << ans << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the number of 
    subarrays with sum equal to `goal` */
    public int numSubarraysWithSum(int[] nums, int goal) {
        
        /* Calculate the number of subarrays with 
        sum exactly equal to `goal` by using the 
        difference between subarrays with sum less
        than or equal to `goal` and those with sum
        less than or equal to `goal-1` */
        return numSubarraysWithSumLessEqualToGoal(nums, goal) - numSubarraysWithSumLessEqualToGoal(nums, goal - 1);
    }
    
    /* Helper function to find the number of 
    subarrays with sum less than or equal to `goal` */
    private int numSubarraysWithSumLessEqualToGoal(int[] nums, int goal) {
        
        /* If goal is negative, there 
        can't be any valid subarray sum */
        if (goal < 0) return 0;
        
        // Pointers to maintain the current window
        int l = 0, r = 0; 
        
        /* Variable to track the current
        sum of elements in the window*/
        int sum = 0;      
        
        // Variable to count the number of subarrays
        int count = 0;   
        
        // Iterate through the array 
        while (r < nums.length) {
            sum += nums[r]; 
            
            /* Shrink the window from the left
            side if the sum exceeds `goal` */
            while (sum > goal) {
                sum -= nums[l];  
                
                // Move the left pointer `l` forward
                l++;            
            }
            
            /* Count all subarrays ending at
            `r` that satisfy the sum condition */
            count += (r - l + 1);
            
            // Move the right pointer `r` forward 
            r++; 
        }
        
        // Return the total count of subarrays
        return count;
    }
    
    public static void main(String[] args) {
        int[] nums = {1, 0, 0, 1, 1, 0};
        int goal = 2;
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        int ans = sol.numSubarraysWithSum(nums, goal);
    
        // Print the result
        System.out.println("Number of substrings with sum \"" + goal + "\" is: " + ans);
    }
}
from typing import List

class Solution:
    """ Function to find the number of 
    subarrays with sum equal to `goal` """
    def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
        """ Calculate the number of subarrays with 
        sum exactly equal to `goal` by using the 
        difference between subarrays with sum less
        than or equal to `goal` and those with sum
        less than or equal to `goal-1` """
        return self.numSubarraysWithSumLessEqualToGoal(nums, goal) - self.numSubarraysWithSumLessEqualToGoal(nums, goal - 1)
    
    """ Helper function to find the number of 
    subarrays with sum less than or equal to `goal` """
    def numSubarraysWithSumLessEqualToGoal(self, nums: List[int], goal: int) -> int:
        """ If goal is negative, there 
        can't be any valid subarray sum """
        if goal < 0:
            return 0
        
        # Pointers to maintain the current window
        l, r = 0, 0 
        
        """ Variable to track the current
        sum of elements in the window"""
        sum_val = 0     
        
        # Variable to count the number of subarrays
        count = 0   
        
        # Iterate through the array 
        while r < len(nums):
            sum_val += nums[r]
            
            """ Shrink the window from the left
            side if the sum exceeds `goal` """
            while sum_val > goal:
                sum_val -= nums[l]
                
                # Move the left pointer `l` forward
                l += 1
            
            """ Count all subarrays ending at
            `r` that satisfy the sum condition """
            count += (r - l + 1)
            
            # Move the right pointer `r` forward 
            r += 1 
        
        # Return the total count of subarrays
        return count

# Example usage:
if __name__ == "__main__":
    nums = [1, 0, 0, 1, 1, 0]
    goal = 2
    
    # Create an instance of Solution class
    sol = Solution()
    
    ans = sol.numSubarraysWithSum(nums, goal)
    
    # Print the result
    print(f"Number of substrings with sum \"{goal}\" is: {ans}")
class Solution {
    /* Function to find the number of 
    subarrays with sum equal to `goal` */
    numSubarraysWithSum(nums, goal) {
        
        /* Calculate the number of subarrays with 
        sum exactly equal to `goal` by using the 
        difference between subarrays with sum less
        than or equal to `goal` and those with sum
        less than or equal to `goal-1` */
        return this.numSubarraysWithSumLessEqualToGoal(nums, goal) - this.numSubarraysWithSumLessEqualToGoal(nums, goal - 1);
    }
    
    /* Helper function to find the number of 
    subarrays with sum less than or equal to `goal` */
    numSubarraysWithSumLessEqualToGoal(nums, goal) {
        
        /* If goal is negative, there 
        can't be any valid subarray sum */
        if (goal < 0) return 0;
        
        // Pointers to maintain the current window
        let l = 0, r = 0; 
        
        /* Variable to track the current 
        sum of elements in the window*/
        let sum = 0;      
        
        // Variable to count the number of subarrays
        let count = 0;   
        
        // Iterate through the array 
        while (r < nums.length) {
            sum += nums[r]; 
            
            /* Shrink the window from the left
            side if the sum exceeds `goal` */
            while (sum > goal) {
                sum -= nums[l];  
                
                // Move the left pointer `l` forward
                l++;            
            }
            
            /* Count all subarrays ending at
            `r` that satisfy the sum condition */
            count += (r - l + 1);
            
            // Move the right pointer `r` forward 
            r++; 
        }
        
        // Return the total count of subarrays
        return count;
    }
}

let nums = [1, 0, 0, 1, 1, 0];
let goal = 2;

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.numSubarraysWithSum(nums, goal);

// Print the result
console.log(`Number of substrings with sum "${goal}" is: ${ans}`);

Complexity Analysis:

Time Complexity:O(2*2N), where N is the size of the string. The outer loop runs for N time and the inner while loop might be running for N time throughout the program. So it becomes O(2N), also the helper function is being called twice so overall time complexity is O(2*2N).

Space Complexity: O(1). There is no extra space being used.

Code

Problem List