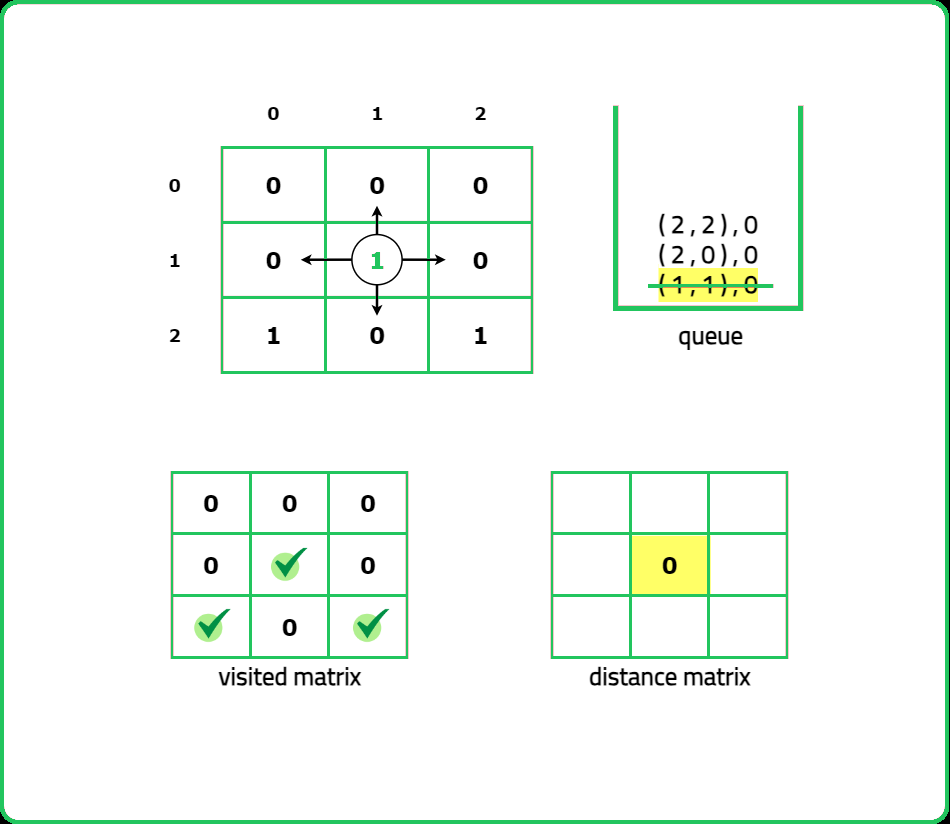
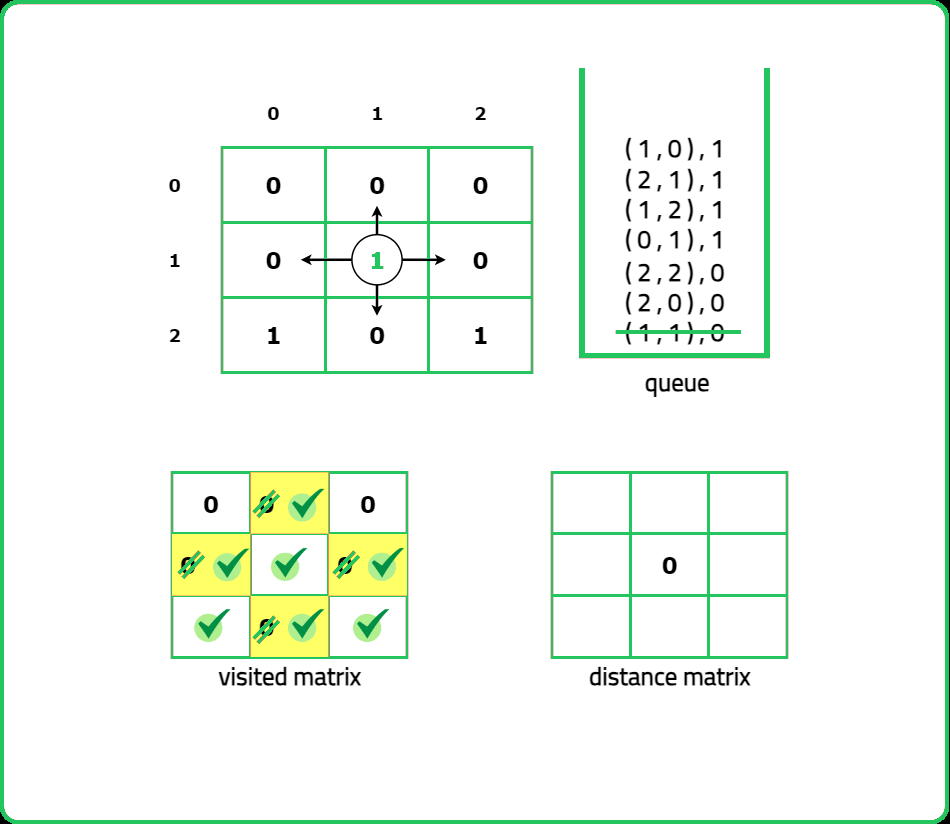
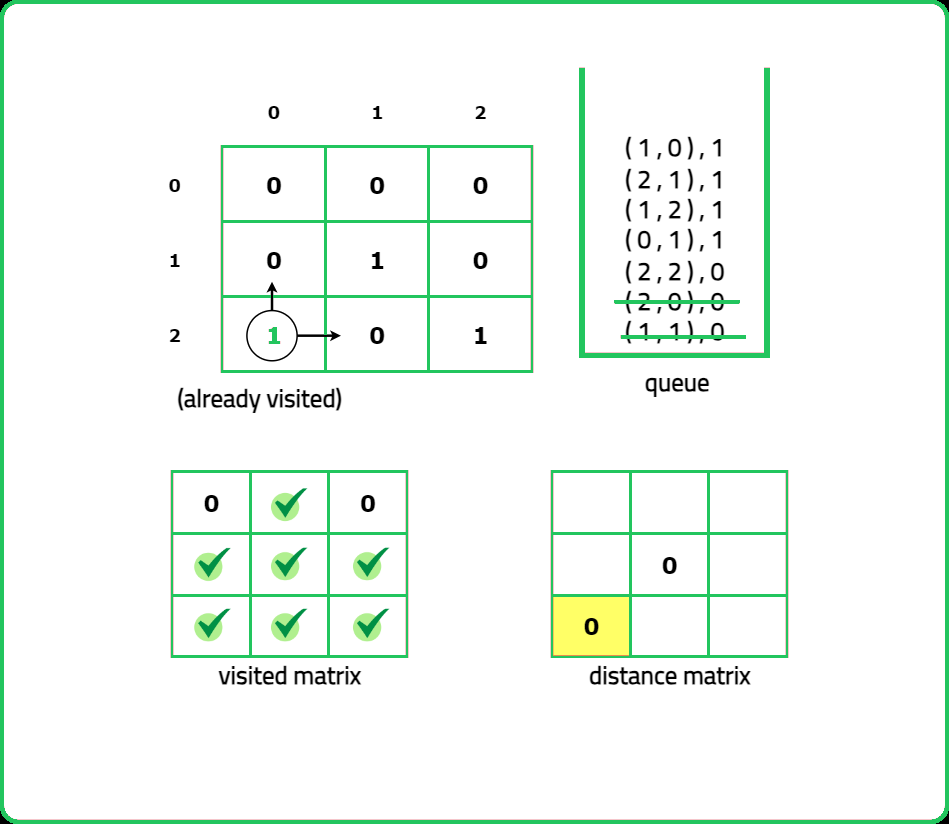
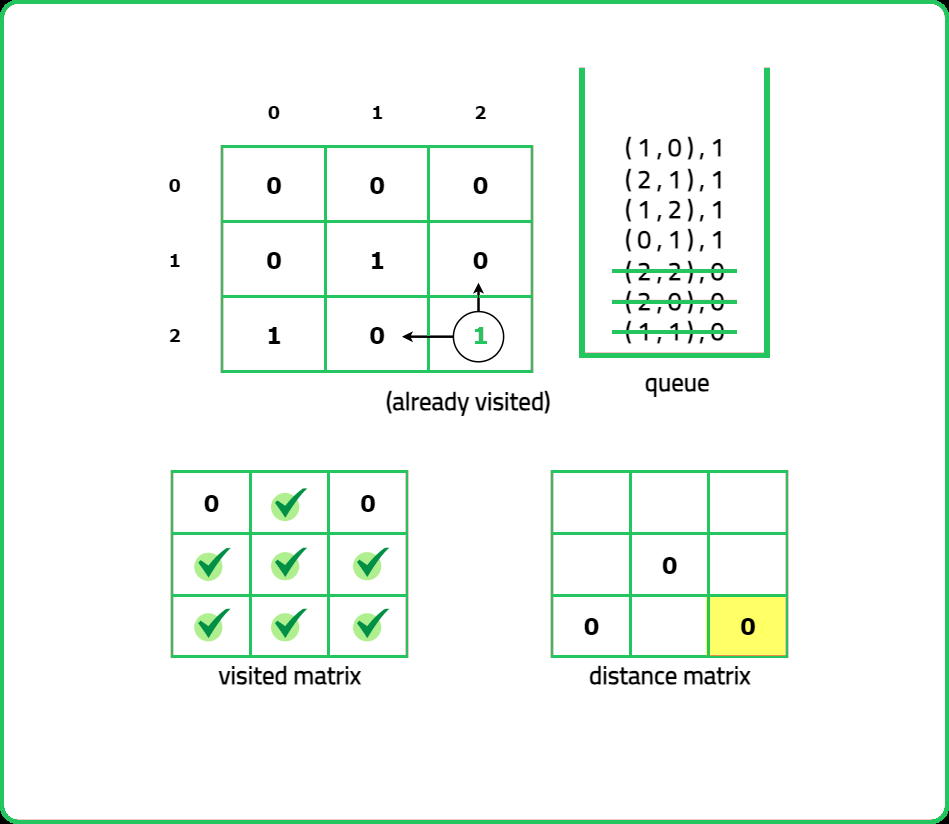
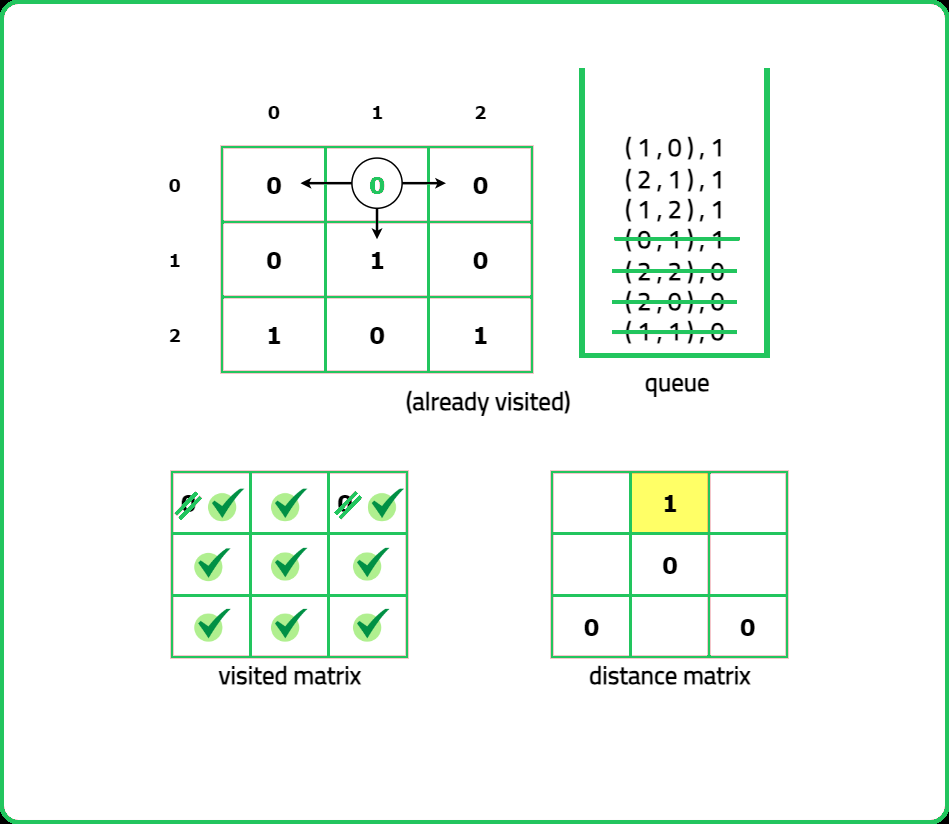
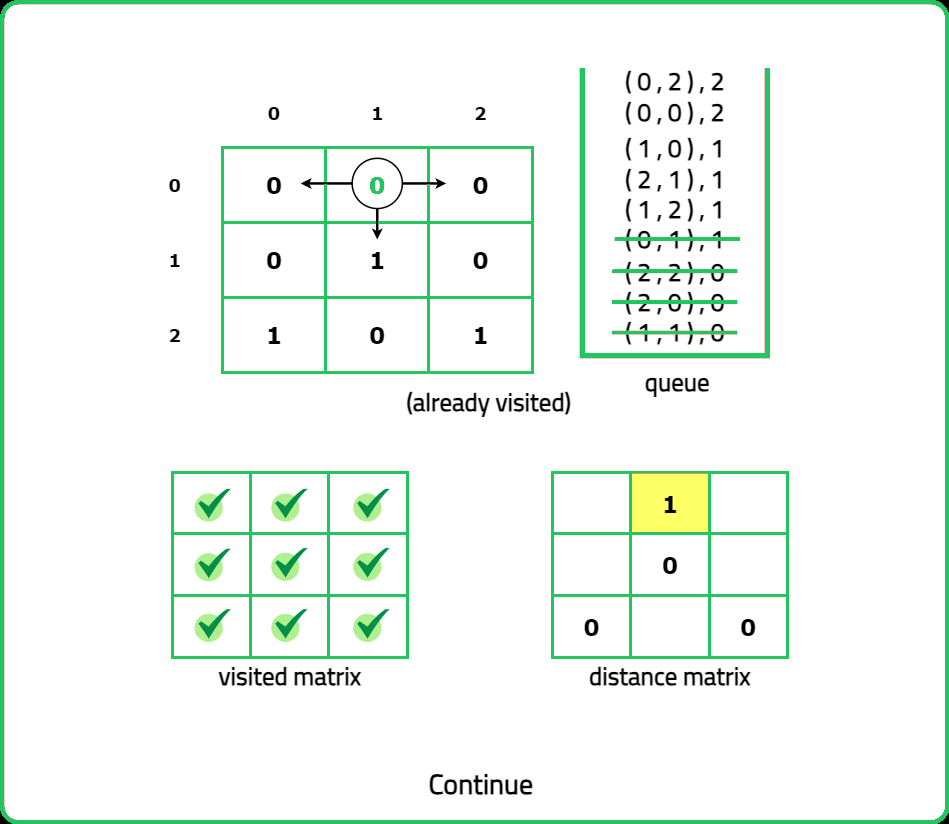
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// DelRow and delCol for neighbors
vector<int> delRow = {-1, 0, 1, 0};
vector<int> delCol = {0, 1, 0, -1};
/* Helper Function to check if a
cell is within boundaries */
bool isValid(int &i, int &j,
int &n, int &m) {
// Return false if cell is invalid
if(i < 0 || i >= n) return false;
if(j < 0 || j >= m) return false;
// Return true if cell is valid
return true;
}
public:
/* Function to find the distance of the
nearest 1 in the grid for each cell. */
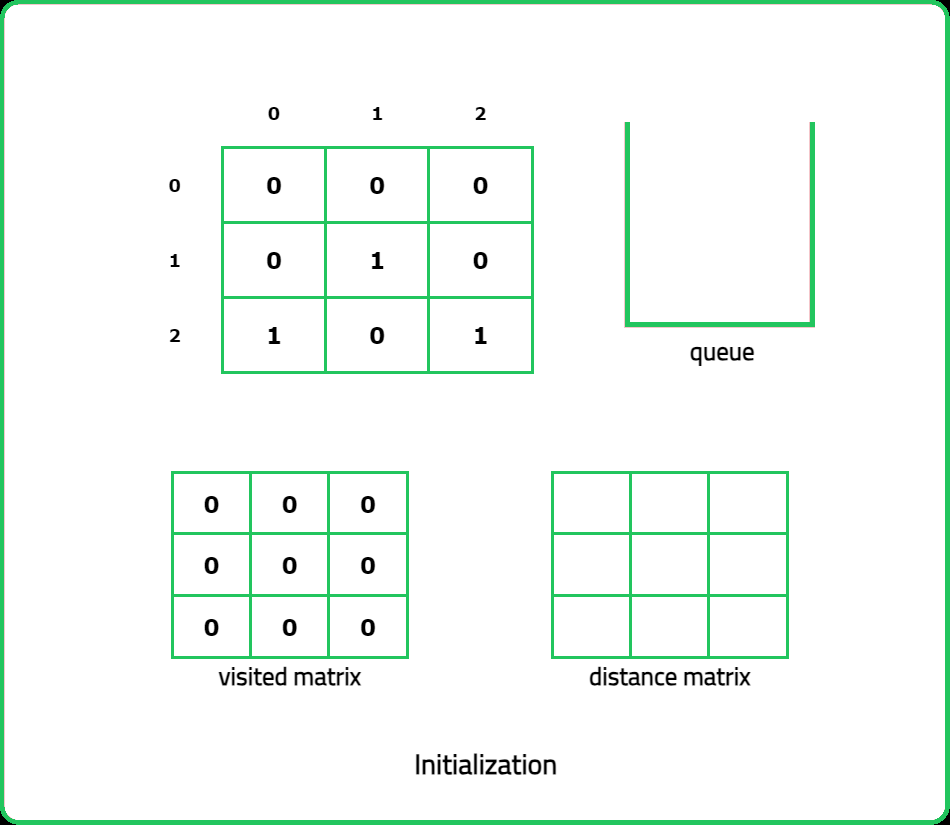
vector<vector<int>>nearest(vector<vector<int>>grid) {
// Determine the dimensions
int n = grid.size();
int m = grid[0].size();
// visited and distance matrix
vector<vector<int>> vis(n, vector<int>(m, 0));
vector<vector<int>> dist(n, vector<int>(m, 0));
// Queue to store the pair {coordinates, steps}
queue<pair<pair<int,int>, int>> q;
// Traverse the matrix
for(int i=0; i < n; i++) {
for(int j=0; j < m; j++) {
// Start BFS if cell contains 1
if(grid[i][j] == 1) {
q.push({{i,j}, 0});
vis[i][j] = 1;
}
else {
// mark unvisited
vis[i][j] = 0;
}
}
}
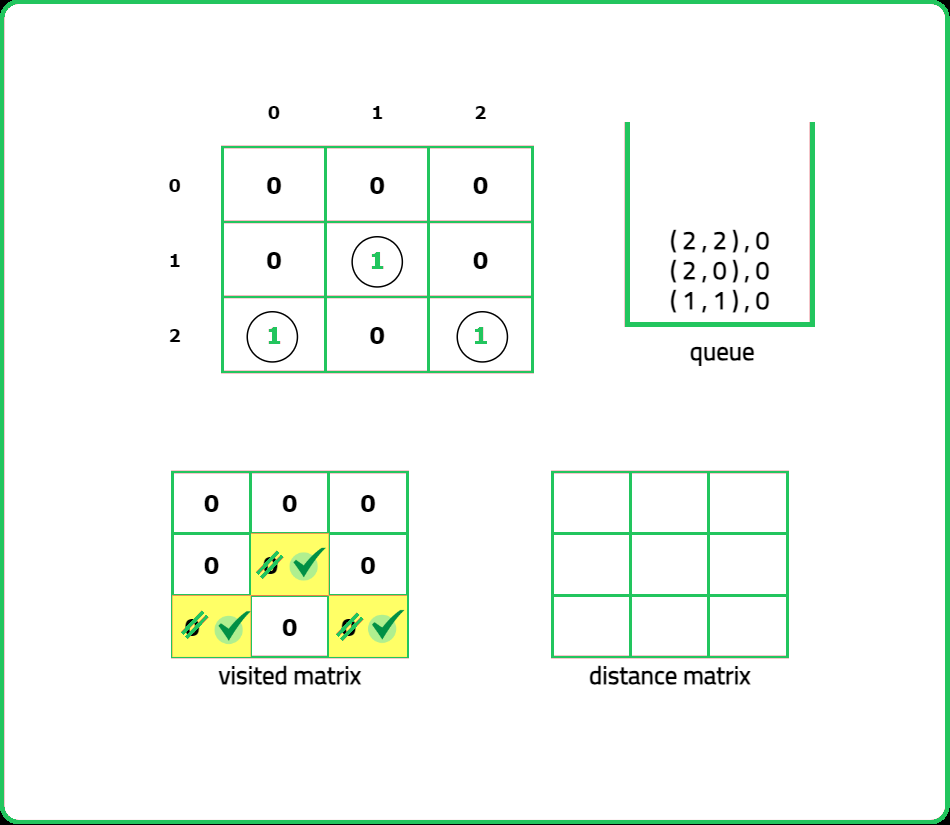
// Traverse till queue becomes empty
while(!q.empty()) {
// Determine the top of queue
auto it = q.front();
q.pop();
// Determine the coordinates of cell
int row = it.first.first;
int col = it.first.second;
// Get the steps
int steps = it.second;
// Update the distance matrix
dist[row][col] = steps;
// Traverse the 4 neighbours
for(int i = 0;i<4;i++) {
// Coordinates of new cell
int nRow = row + delRow[i];
int nCol = col + delCol[i];
// Check for valid, unvisited cell
if(isValid(nRow, nCol, n, m)
&& vis[nRow][nCol] == 0) {
// Mark the cell as visited
vis[nRow][nCol] = 1;
q.push({{nRow, nCol}, steps+1});
}
}
}
// return distance matrix
return dist;
}
};
int main() {
vector<vector<int>> grid = {
{0, 1, 1, 0},
{1, 1, 0, 0},
{0, 0, 1, 1}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the distance of the
nearest 1 in the grid for each cell. */
vector<vector<int>> ans = sol.nearest(grid);
int n = ans.size();
int m = ans[0].size();
// Output
cout << "The distance of the nearest 1 in the grid for each cell is: " << endl;
for(int i=0; i < n; i++) {
for(int j=0; j < m; j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120
import java.util.*;
class Solution {
// DelRow and delCol for neighbors
private int[] delRow = {-1, 0, 1, 0};
private int[] delCol = {0, 1, 0, -1};
/* Helper Function to check if a
the cell is within boundaries */
private boolean isValid(int i, int j,
int n, int m) {
// Return false if the cell is invalid
if(i < 0 || i >= n) return false;
if(j < 0 || j >= m) return false;
// Return true if the cell is valid
return true;
}
/* Function to find the distance of the
nearest 1 in the grid for each cell. */
public int[][] nearest(int[][] grid) {
// Determine the dimensions
int n = grid.length;
int m = grid[0].length;
// visited and distance matrix
int[][] vis = new int[n][m];
int[][] dist = new int[n][m];
// Queue to store the pair {coordinates, steps}
Queue<int[]> q = new LinkedList<>();
// Traverse the matrix
for(int i=0; i < n; i++) {
for(int j=0; j < m; j++) {
// Start BFS if the cell contains 1
if(grid[i][j] == 1) {
q.add(new int[]{i, j, 0});
vis[i][j] = 1;
}
else {
// mark unvisited
vis[i][j] = 0;
}
}
}
// Traverse till the queue becomes empty
while(!q.isEmpty()) {
// Determine the top of the queue
int[] it = q.poll();
// Determine the coordinates of the cell
int row = it[0];
int col = it[1];
// Get the steps
int steps = it[2];
// Update the distance matrix
dist[row][col] = steps;
// Traverse the 4 neighbors
for(int i = 0; i < 4; i++) {
// Coordinates of new cell
int nRow = row + delRow[i];
int nCol = col + delCol[i];
// Check for valid, unvisited cell
if(isValid(nRow, nCol, n, m) &&
vis[nRow][nCol] == 0) {
// Mark the cell as visited
vis[nRow][nCol] = 1;
q.add(new int[]{nRow, nCol, steps + 1});
}
}
}
// return distance matrix
return dist;
}
}
public class Main {
public static void main(String[] args) {
int[][] grid = {
{0, 1, 1, 0},
{1, 1, 0, 0},
{0, 0, 1, 1}
};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the distance of the
nearest 1 in the grid for each cell. */
int[][] ans = sol.nearest(grid);
int n = ans.length;
int m = ans[0].length;
// Output
System.out.println("The distance of the nearest 1 in the grid for each cell is: ");
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
System.out.print(ans[i][j] + " ");
}
System.out.println();
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101
from collections import deque
class Solution:
# delRow and delCol for neighbors
delRow = [-1, 0, 1, 0]
delCol = [0, 1, 0, -1]
# Helper Function to check if a
# the cell is within boundaries
def isValid(self, i, j, n, m):
# Return false if the cell is invalid
if i < 0 or i >= n: return False
if j < 0 or j >= m: return False
# Return true if the cell is valid
return True
# Function to find the distance of the
# nearest 1 in the grid for each cell.
def nearest(self, grid):
# Determine the dimensions
n = len(grid)
m = len(grid[0])
# visited and distance matrix
vis = [[0 for _ in range(m)] for _ in range(n)]
dist = [[0 for _ in range(m)] for _ in range(n)]
# Queue to store the pair {coordinates, steps}
q = deque()
# Traverse the matrix
for i in range(n):
for j in range(m):
# Start BFS if the cell contains 1
if grid[i][j] == 1:
q.append(((i, j), 0))
vis[i][j] = 1
else:
# mark unvisited
vis[i][j] = 0
# Traverse till the queue becomes empty
while q:
# Determine the top of the queue
it = q.popleft()
# Determine the coordinates of the cell
row, col = it[0]
# Get the steps
steps = it[1]
# Update the distance matrix
dist[row][col] = steps
# Traverse the 4 neighbors
for i in range(4):
# Coordinates of new cell
nRow = row + self.delRow[i]
nCol = col + self.delCol[i]
# Check for valid, unvisited cell
if (self.isValid(nRow, nCol, n, m) and
vis[nRow][nCol] == 0):
# Mark the cell as visited
vis[nRow][nCol] = 1
q.append(((nRow, nCol), steps + 1))
# return distance matrix
return dist
if __name__ == "__main__":
grid = [
[0, 1, 1, 0],
[1, 1, 0, 0],
[0, 0, 1, 1]
]
# Creating an instance of Solution class
sol = Solution()
# Function call to find the distance of the
# nearest 1 in the grid for each cell.
ans = sol.nearest(grid)
n = len(ans)
m = len(ans[0])
# Output
print("The distance of the nearest 1 in the grid for each cell is: ")
for i in range(n):
for j in range(m):
print(ans[i][j], end = " ")
print()
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125
class Solution {
constructor() {
// delRow and delCol for neighbors
this.delRow = [-1, 0, 1, 0];
this.delCol = [0, 1, 0, -1];
}
/* Helper Function to check if a
the cell is within boundaries */
isValid(i, j, n, m) {
// Return false if the cell is invalid
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if the cell is valid
return true;
}
/* Function to find the distance of the
nearest 1 in the grid for each cell. */
nearest(grid) {
// Determine the dimensions
let n = grid.length;
let m = grid[0].length;
// visited and distance matrix
let vis = Array.from(
{ length: n },
() => Array(m).fill(0)
);
let dist = Array.from(
{ length: n },
() => Array(m).fill(0)
);
// Queue to store the pair {coordinates, steps}
let q = [];
// Traverse the matrix
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
// Start BFS if the cell contains 1
if (grid[i][j] === 1) {
q.push([[i, j], 0]);
vis[i][j] = 1;
} else {
// mark unvisited
vis[i][j] = 0;
}
}
}
// Traverse till the queue becomes empty
while (q.length > 0) {
// Determine the top of the queue
let it = q.shift();
// Determine the coordinates of the cell
let row = it[0][0];
let col = it[0][1];
// Get the steps
let steps = it[1];
// Update the distance matrix
dist[row][col] = steps;
// Traverse the 4 neighbors
for (let i = 0; i < 4; i++) {
// Coordinates of new cell
let nRow = row + this.delRow[i];
let nCol = col + this.delCol[i];
// Check for valid, unvisited cell
if (this.isValid(nRow, nCol, n, m)
&& vis[nRow][nCol] === 0) {
// Mark the cell as visited
vis[nRow][nCol] = 1;
q.push([[nRow, nCol], steps + 1]);
}
}
}
// return distance matrix
return dist;
}
}
let main = () => {
let grid = [
[0, 1, 1, 0],
[1, 1, 0, 0],
[0, 0, 1, 1]
];
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to find the distance of
the nearest 1 in the grid for each cell. */
let ans = sol.nearest(grid);
let n = ans.length;
let m = ans[0].length;
// Output
console.log("The distance of the nearest 1 in the grid for each cell is: ");
for (let i = 0; i < n; i++) {
let row = "";
for (let j = 0; j < m; j++) {
row += ans[i][j] + " ";
}
console.log(row.trim());
}
}
main();