Max Consecutive Ones III
Sliding Window / 2 Pointer
Longest and Smallest Window Problems
Hard
- Fun Fact: This programming problem is a pragmatic application of the "sliding window" concept used in fields like video streaming and networking protocols
- By controlling the number of bits that can be flipped in a buffer (representing data or packets), developers can optimize data loss or error handling
- Algorithms like these help smooth your Netflix binges, ensuring your video doesn't stutter even if some data packets arrive out of order or get lost!
Given a binary array nums and an integer k, flip at most k 0's.
Return the maximum number of consecutive 1's after performing the flipping operation.
Examples:
Input : nums = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0] , k = 3
Output : 10
Explanation : The maximum number of consecutive 1's are obtained only if we flip the 0's present at position 3, 4, 5 (0 base indexing).
The array after flipping becomes [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0].
The number of consecutive 1's is 10.
Input : nums = [0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1] , k = 3
Output : 9
Explanation : The underlines 1's are obtained by flipping 0's in the new array.
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1].
The number of consecutive 1's is 9.
Input : nums = [1, 1, 0, 0, 1] , k = 3
Constraints
- 1 <= nums.length <= 105
- 0 <= nums[i] <= 1
- 0 <= k <= nums.length
Hints
- "Use a sliding window to maintain a range of elements where at most k 0s are flipped into 1s. Keep a counter for the number of 0s in the current window. When the counter exceeds k, move the left pointer forward while decrementing the count of 0s if the leftmost element is 0."
- "At each step, calculate the length of the current valid window as right−left+1. Update the maximum length whenever a larger valid window is found. "
Company Tags
Roche
American Express
HCL Technologies
JPMorgan Chase
Target
Zoho
Etsy
Walmart
eBay
Zomato
Red Hat
Unity Technologies
NVIDIA
Splunk
Morgan Stanley
Lyft
ARM
Byju's
Reddit
Goldman Sachs
Epic Games
Instacart
KPMG
IBM
Chewy
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The idea here is to generate all possible substrings of the given array and while doing so, keep a track of all the zeros encountered so far in the substring. If the number of zeros exceeds k then no need to consider that substring, else calculate the length of the current substring and update the maximum length of substring.
Approach:
zero to 0 to keep track number of zeros found so far in the substring.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the length of the
longest substring with at most k zeros*/
int longestOnes(vector<int>& nums, int k) {
// Length of the input array
int n = nums.size();
//Maximum length of the substring
int maxLen = 0;
/* Variable to count the number
of zeros in the current window*/
int zeros = 0;
/* Iterate through all possible
starting points of the substring*/
for (int i = 0; i < n; i++) {
zeros = 0;
/* Expand the window from starting
point i to the end of the array*/
for (int j = i; j < n; j++) {
if (nums[j] == 0) {
/* Increment zeros count
when encountering a zero*/
zeros++;
}
/* If zeros count is within the
allowed limit (k), update maxLen*/
if (zeros <= k) {
// Calculate the length of substring
int len = j - i + 1;
maxLen = max(maxLen, len);
} else break;
}
}
//Return the maximum length
return maxLen;
}
};
int main() {
vector<int> input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol;
int length = sol.longestOnes(input, k);
// Print the result
cout << "Length of longest substring with at most " << k << " zeros: " << length << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162
import java.util.*;
class Solution {
/* Function to find the length of the
longest substring with at most k zeros */
public int longestOnes(int[] nums, int k) {
// Length of the input array
int n = nums.length;
// Maximum length of the substring
int maxLen = 0;
/* Variable to count the number
of zeros in the current window */
int zeros = 0;
/* Iterate through all possible
starting points of the substring */
for (int i = 0; i < n; i++) {
zeros = 0;
/* Expand the window from starting
point i to the end of the array */
for (int j = i; j < n; j++) {
if (nums[j] == 0) {
/* Increment zeros count
when encountering a zero */
zeros++;
}
/* If zeros count is within the
allowed limit (k), update maxLen */
if (zeros <= k) {
// Calculate the length of substring
int len = j - i + 1;
maxLen = Math.max(maxLen, len);
} else break;
}
}
// Return the maximum length
return maxLen;
}
public static void main(String[] args) {
int[] input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol = new Solution();
int length = sol.longestOnes(input, k);
// Print the result
System.out.println("Length of longest substring with at most " + k + " zeros: " + length);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
class Solution:
""" Function to find the length of the
longest substring with at most k zeros"""
def longestOnes(self, nums, k):
# Length of the input array
n = len(nums)
# Maximum length of the substring
maxLen = 0
""" Variable to count the number
of zeros in the current window """
zeros = 0
""" Iterate through all possible
starting points of the substring """
for i in range(n):
zeros = 0
""" Expand the window from starting
point i to the end of the array """
for j in range(i, n):
if nums[j] == 0:
""" Increment zeros count
when encountering a zero """
zeros += 1
""" If zeros count is within the
allowed limit (k), update maxLen """
if zeros <= k:
# Calculate the length of substring
length = j - i + 1
maxLen = max(maxLen, length)
else:
break
# Return the maximum length
return maxLen
if __name__ == "__main__":
input_arr = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0]
k = 2
# Create an instance of Solution class
sol = Solution()
length = sol.longestOnes(input_arr, k)
# Print the result
print(f"Length of longest substring with at most {k} zeros: {length}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
class Solution {
/*Function to find the length of the
longest substring with at most k zeros*/
longestOnes(nums, k) {
// Length of the input array
let n = nums.length;
// Maximum length of the substring
let maxLen = 0;
/* Variable to count the number
of zeros in the current window */
let zeros = 0;
/* Iterate through all possible
starting points of the substring */
for (let i = 0; i < n; i++) {
zeros = 0;
/* Expand the window from starting
point i to the end of the array */
for (let j = i; j < n; j++) {
if (nums[j] === 0) {
/* Increment zeros count
when encountering a zero */
zeros++;
}
/* If zeros count is within the
allowed limit (k), update maxLen */
if (zeros <= k) {
// Calculate the length of substring
let len = j - i + 1;
maxLen = Math.max(maxLen, len);
} else break;
}
}
// Return the maximum length
return maxLen;
}
}
function main() {
let input = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0];
let k = 2;
// Create an instance of Solution class
let sol = new Solution();
let length = sol.longestOnes(input, k);
// Print the result
console.log(`Length of longest substring with at most ${k} zeros: ${length}`);
}
// Invoke main function
main();
Complexity Analysis:
Time Complexity:O(N2), where N is the size of the array. As for every element of the array the inner loop runs for N times.Space Complexity: O(1) as no extra space is being used.
Intuition:
The idea here is to use sliding window technique to solve this problem in linear time. The sliding window technique is chosen because it efficiently manages a window within the input array that meets specific criteria. It dynamically adjusts the size and position of the window based on the number of zeros encountered to ensure the that the number of zeros are less than and equal to k.
Approach:
zeros to keep track of the number of zeros encountered within the current window, maxLen to store the maximum length of the substring found so far.12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the length of the
longest substring with at most k zeros */
int longestOnes(vector<int>& nums, int k) {
// Length of the input array
int n = nums.size();
// Pointers for sliding window approach
int l = 0, r = 0;
/* Variables to count zeros
and store maximum length*/
int zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach*/
while(r < n){
if(nums[r] == 0){
/* Increment zeros count
when encountering a zero*/
zeros++;
}
while(zeros > k){
if(nums[l] == 0){
/* Decrement zeros count
when moving left pointer*/
zeros--;
}
/* Move left pointer to the
right to shrink the window*/
l++;
}
/* Calculate the length
of current substring*/
int len = r - l + 1;
/* Update maxLen if the current
substring length is greater*/
maxLen = max(maxLen, len);
/* Move right pointer
to expand the window*/
r++;
}
// Return the maximum length
return maxLen;
}
};
int main() {
vector<int> input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol;
int length = sol.longestOnes(input, k);
// Print the result
cout << "Length of longest substring with at most " << k << " zeros: " << length << endl;
return 0;
}1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
import java.util.*;
class Solution {
/* Function to find the length of the
longest substring with at most k zeros */
public int longestOnes(int[] nums, int k) {
// Length of the input array
int n = nums.length;
// Pointers for sliding window approach
int l = 0, r = 0;
/* Variables to count zeros
and store maximum length */
int zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach */
while(r < n){
if(nums[r] == 0){
/* Increment zeros count
when encountering a zero */
zeros++;
}
while(zeros > k){
if(nums[l] == 0){
/* Decrement zeros count
when moving left pointer */
zeros--;
}
/* Move left pointer to the
right to shrink the window */
l++;
}
/* Calculate the length
of current substring */
int len = r - l + 1;
/* Update maxLen if the current
substring length is greater */
maxLen = Math.max(maxLen, len);
/* Move right pointer
to expand the window */
r++;
}
// Return the maximum length
return maxLen;
}
public static void main(String[] args) {
int[] input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol = new Solution();
int length = sol.longestOnes(input, k);
// Print the result
System.out.println("Length of longest substring with at most " + k + " zeros: " + length);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
class Solution:
""" Function to find the length of the
longest substring with at most k zeros """
def longestOnes(self, nums, k):
# Length of the input array
n = len(nums)
# Pointers for sliding window approach
l, r = 0, 0
""" Variables to count zeros
and store maximum length """
zeros, maxLen = 0, 0
""" Iterate through the array
using sliding window approach """
while r < n:
if nums[r] == 0:
""" Increment zeros count
when encountering a zero """
zeros += 1
while zeros > k:
if nums[l] == 0:
""" Decrement zeros count
when moving left pointer """
zeros -= 1
""" Move left pointer to the
right to shrink the window """
l += 1
""" Calculate the length
of current substring """
length = r - l + 1
""" Update maxLen if the current
substring length is greater """
maxLen = max(maxLen, length)
""" Move right pointer
to expand the window """
r += 1
# Return the maximum length
return maxLen
if __name__ == "__main__":
input_arr = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0]
k = 2
# Create an instance of Solution class
sol = Solution()
length = sol.longestOnes(input_arr, k)
# Print the result
print(f"Length of longest substring with at most {k} zeros: {length}")123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
class Solution {
/* Function to find the length of the
longest substring with at most k zeros */
longestOnes(nums, k) {
// Length of the input array
let n = nums.length;
// Pointers for sliding window approach
let l = 0, r = 0;
/* Variables to count zeros
and store maximum length */
let zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach */
while(r < n){
if(nums[r] === 0){
/* Increment zeros count
when encountering a zero */
zeros++;
}
while(zeros > k){
if(nums[l] === 0){
/* Decrement zeros count
when moving left pointer */
zeros--;
}
/* Move left pointer to the
right to shrink the window */
l++;
}
/* Calculate the length
of current substring */
let len = r - l + 1;
/* Update maxLen if the current
substring length is greater */
maxLen = Math.max(maxLen, len);
/* Move right pointer
to expand the window */
r++;
}
// Return the maximum length
return maxLen;
}
}
let input = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0];
let k = 2;
// Create an instance of Solution class
let sol = new Solution();
let len = sol.longestOnes(input, k);
// Print the result
console.log(`Length of longest substring with at most ${k} zeros: ${len}`);
Complexity Analysis:
Time Complexity:O(2N), where N is the size of the array. The outer and the inner loop is running for N times each.Space Complexity: O(1) as no extra space is being used.
Intuition:
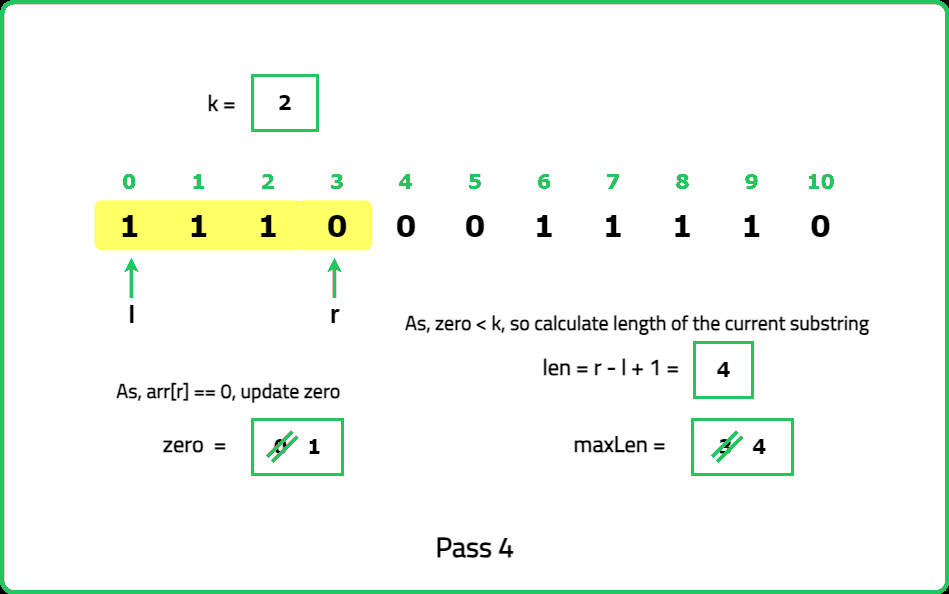
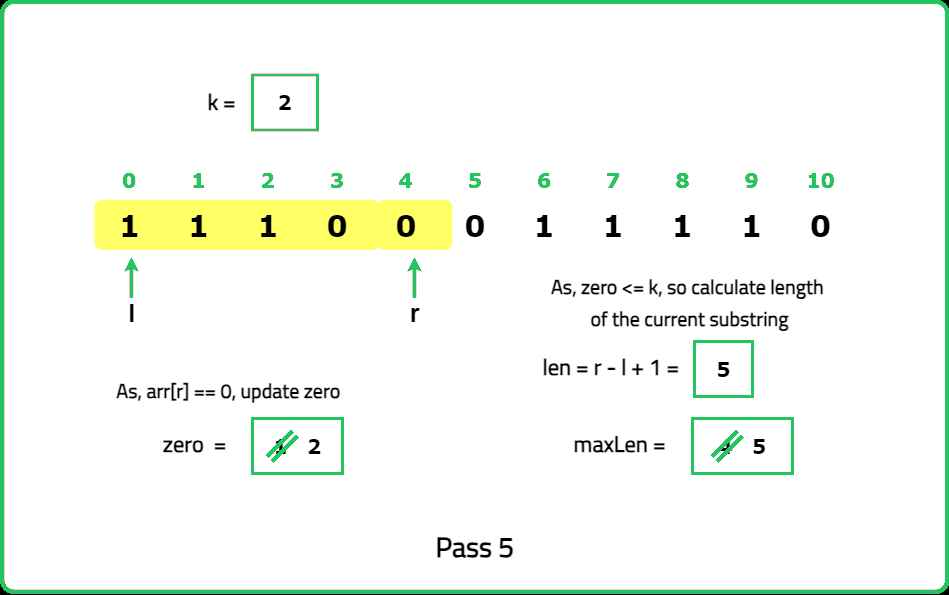
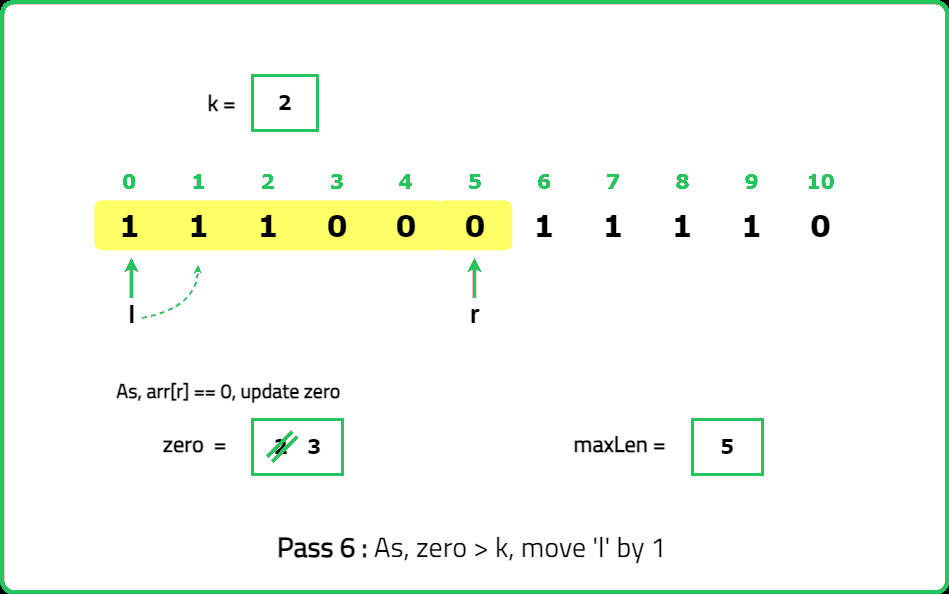
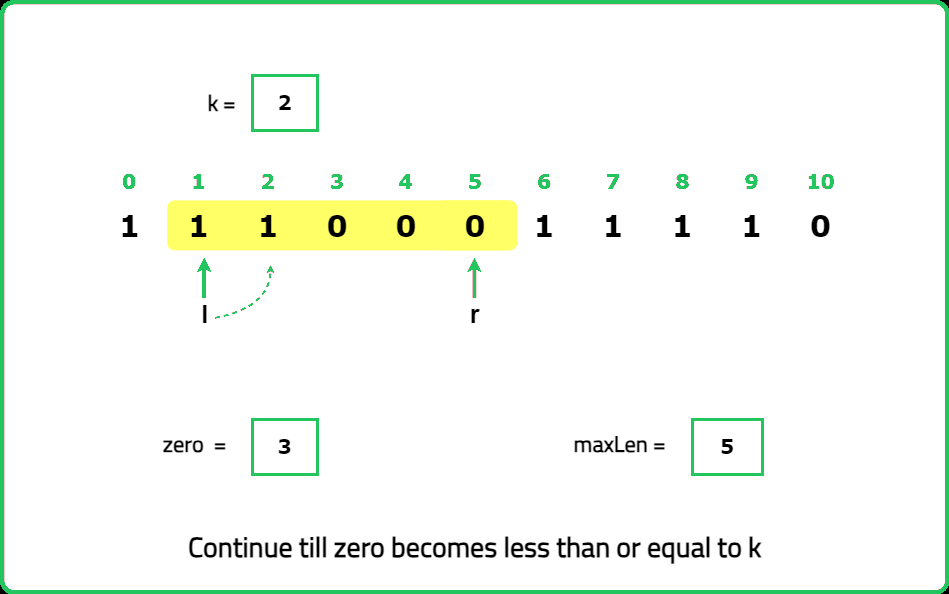
The idea here is to employ the sliding window approach efficiently by avoiding the additional O(N) time complexity incurred when shifting the window entirely in the better solution, to ensure that the total number of zeros does not exceed k. Instead of moving the left pointer (l) to eliminate excess zeros completely, shift the window by one position at a time. This method ensures that the problem can be solved in O(N) time complexity only.
Approach:
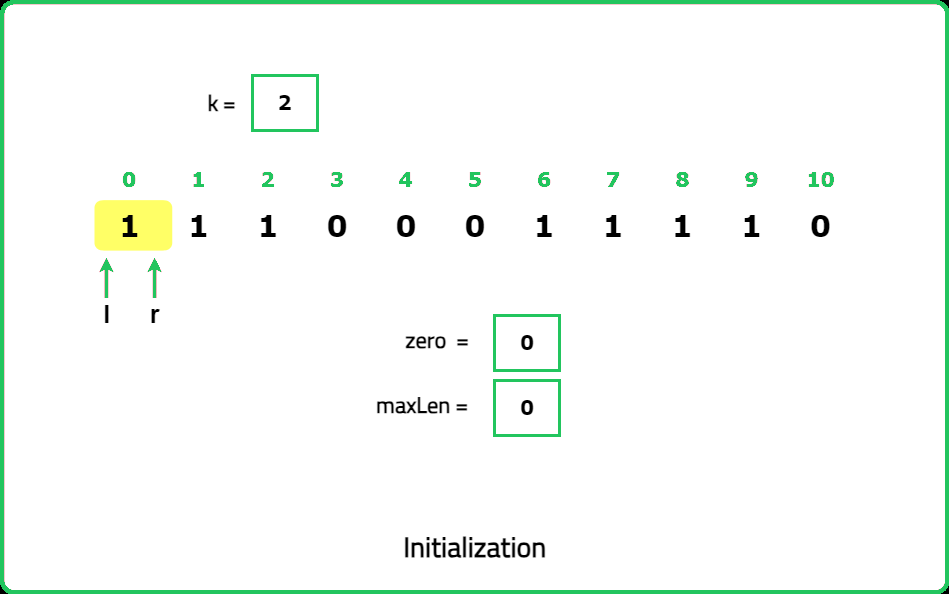
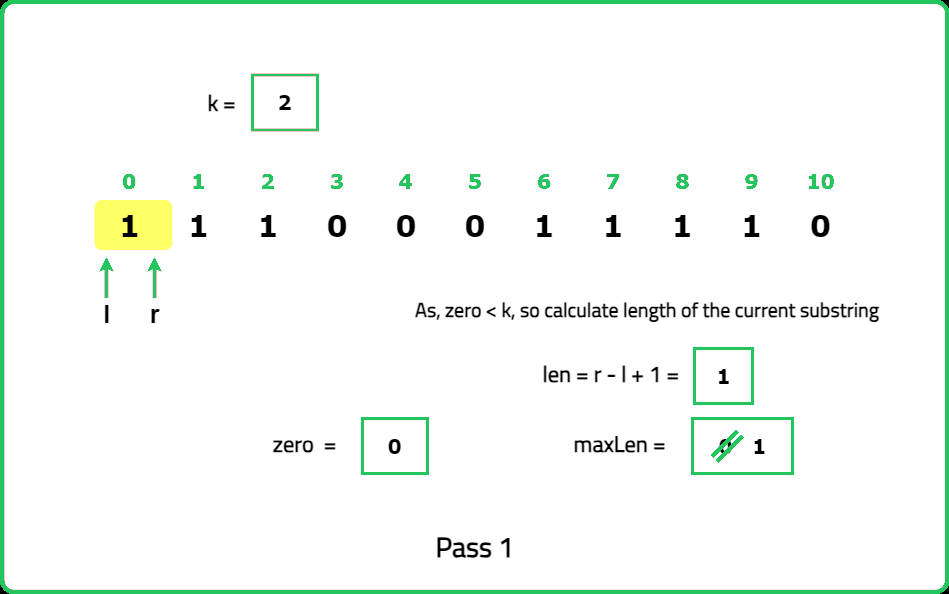
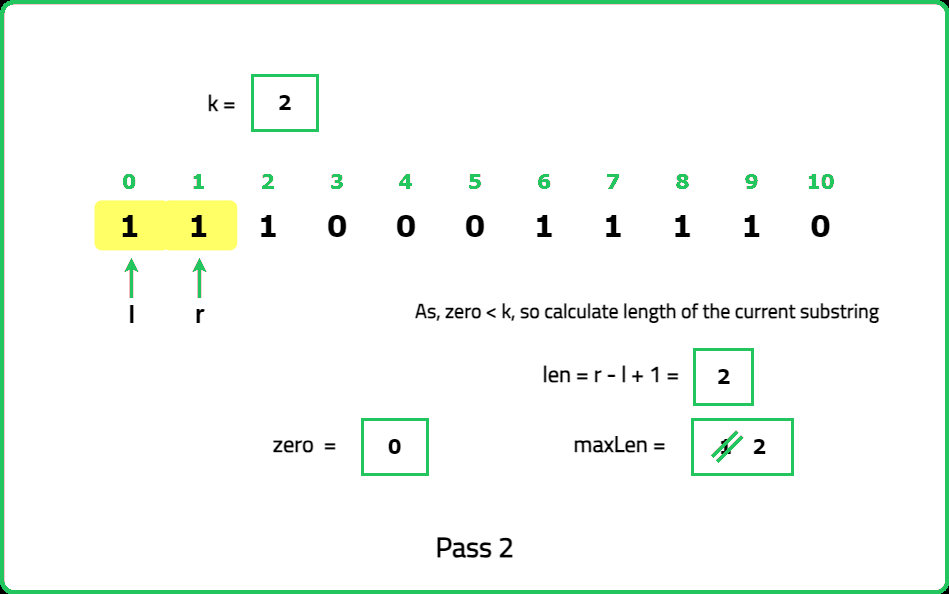
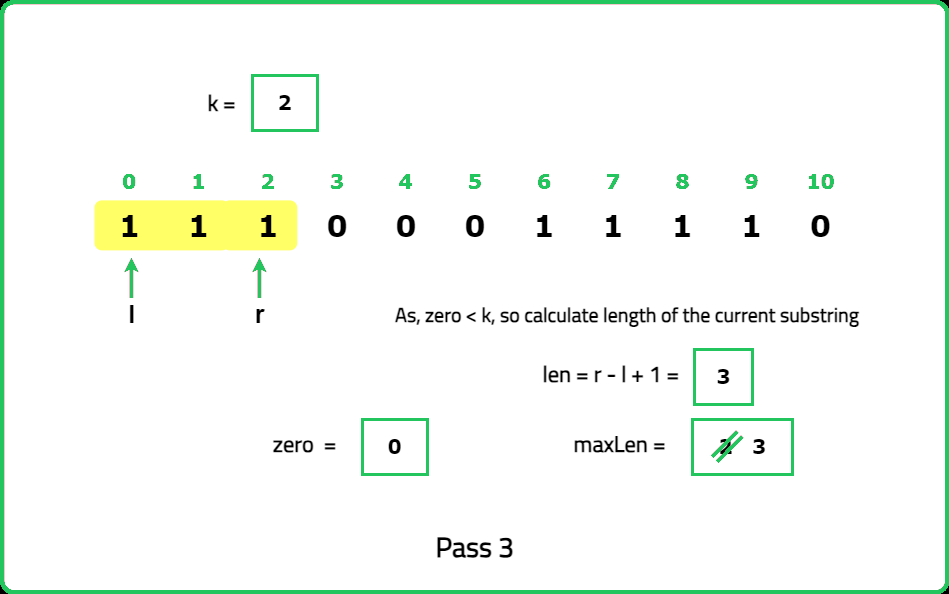
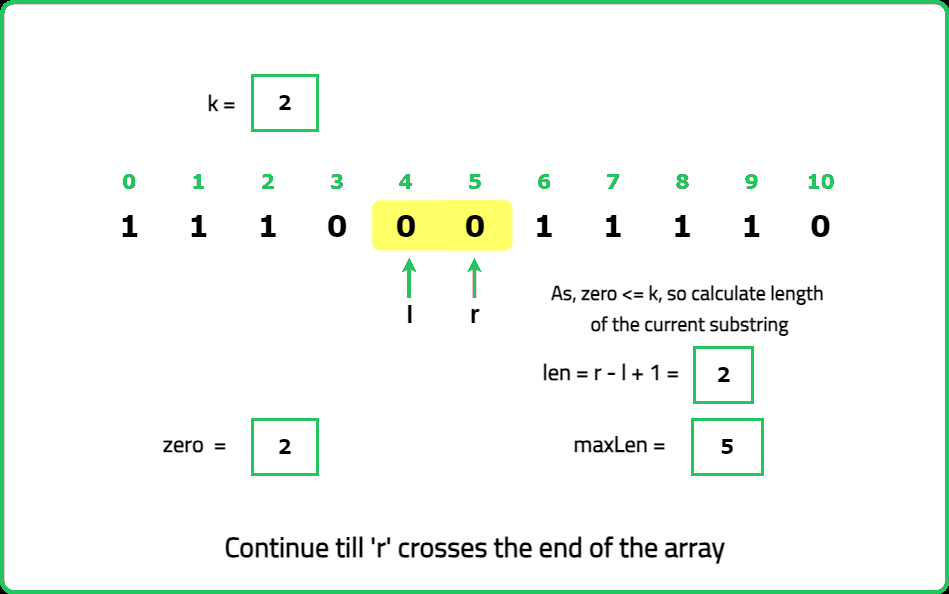
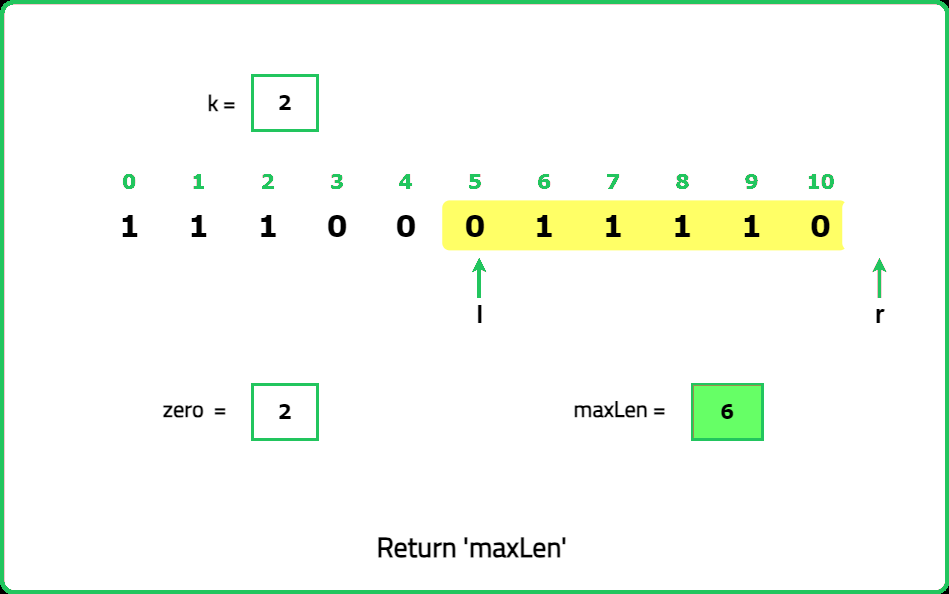
zeros to count the number of zeros encountered within the current window, maxLen to store the maximum length of valid substrings found.Dry Run:
<!---<img src="https://static.takeuforward.org/premium/Sliding Window and 2 Pointer/Longest and Smallest Window Problems/Max Consecutive Ones III/31-s3EDt1P3">
Please refer to the video for complete dry-run.
---!>
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the length of the
longest substring with at most k zeros */
int longestOnes(vector<int>& nums, int k) {
// Length of the input array
int n = nums.size();
// Pointers for sliding window approach
int l = 0, r = 0;
/* Variables to count zeros
and store maximum length */
int zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach */
while (r < n) {
if(nums[r] == 0) zeros++;
if (zeros > k) {
if (nums[l] == 0) {
/* Decrement zeros count
when moving left pointer */
zeros--;
}
l++;
}
if(zeros <= k){
/* Calculate the length
of current substring */
int len = r - l + 1;
/* Update maxLen if the current
substring length is greater */
maxLen = max(maxLen, len);
}
r++;
}
// Return the maximum length
return maxLen;
}
};
int main() {
vector<int> input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol;
int length = sol.longestOnes(input, k);
// Print the result
cout << "Length of longest substring with at most " << k << " zeros: " << length << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162
import java.util.*;
class Solution {
/* Function to find the length of the
longest substring with at most k zeros */
public int longestOnes(int[] nums, int k) {
// Length of the input array
int n = nums.length;
// Pointers for sliding window approach
int l = 0, r = 0;
/* Variables to count zeros
and store maximum length */
int zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach */
while (r < n) {
if(nums[r] == 0) zeros++;
if (zeros > k) {
if (nums[l] == 0) {
/* Decrement zeros count
when moving left pointer */
zeros--;
}
l++;
}
if(zeros <= k){
/* Calculate the length
of current substring */
int len = r - l + 1;
/* Update maxLen if the current
substring length is greater */
maxLen = Math.max(maxLen, len);
}
r++;
}
// Return the maximum length
return maxLen;
}
public static void main(String[] args) {
int[] input = {1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0};
int k = 2;
// Create an instance of Solution class
Solution sol = new Solution();
int length = sol.longestOnes(input, k);
// Print the result
System.out.println("Length of longest substring with at most " + k + " zeros: " + length);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
class Solution:
""" Function to find the length of the
longest substring with at most k zeros """
def longestOnes(self, nums, k):
# Length of the input array
n = len(nums)
# Pointers for sliding window approach
l, r = 0, 0
""" Variables to count zeros
and store maximum length """
zeros, maxLen = 0, 0
""" Iterate through the array
using sliding window approach """
while r < n:
if nums[r] == 0:
zeros += 1
if zeros > k:
if nums[l] == 0:
""" Decrement zeros count
when moving left pointer """
zeros -= 1
l += 1
if zeros <= k:
""" Calculate the length
of current substring """
length = r - l + 1
""" Update maxLen if the current
substring length is greater """
maxLen = max(maxLen, length)
r += 1
# Return the maximum length
return maxLen
if __name__ == "__main__":
input_nums = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0]
k = 2
# Create an instance of Solution class
sol = Solution()
length = sol.longestOnes(input_nums, k)
# Print the result
print(f"Length of longest substring with at most {k} zeros: {length}")123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
class Solution {
/*Function to find the length of the
longest substring with at most k zeros*/
longestOnes(nums, k) {
// Length of the input array
let n = nums.length;
// Pointers for sliding window approach
let l = 0, r = 0;
/* Variables to count zeros
and store maximum length */
let zeros = 0, maxLen = 0;
/* Iterate through the array
using sliding window approach */
while (r < n) {
if(nums[r] == 0) zeros++;
if (zeros > k) {
if (nums[l] == 0) {
/* Decrement zeros count
when moving left pointer */
zeros--;
}
l++;
}
if(zeros <= k){
/* Calculate the length
of current substring */
let len = r - l + 1;
/* Update maxLen if the current
substring length is greater */
maxLen = Math.max(maxLen, len);
}
r++;
}
// Return the maximum length
return maxLen;
}
}
let input = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0];
let k = 2;
// Create an instance of Solution class
let sol = new Solution();
let len = sol.longestOnes(input, k);
// Print the result
console.log(`Length of longest substring with at most ${k} zeros: ${len}`);
Complexity Analysis:
Time Complexity:O(N), where N is the size of the array. As for every element , the loop run N times.Space Complexity: O(1) as no extra space is being used.
Frequently Occurring Doubts
Q: What happens if nums contains no 0s?
A: If the array contains no 0s, the entire array is already the longest subarray of consecutive 1s. The output will be n, where n is the length of the array.
Q: Can k be greater than the number of 0s in the array?
A: Yes, in this case, all 0s can be flipped, and the result will be the length of the entire array, as all elements can become 1.
Interview Followup Questions
Q: How would you modify the solution to return the indices of the longest subarray?
A: Track the start and end indices of the current window whenever a new maximum length is found. Return these indices along with the length.
Q: How would the problem change if flipping 1s into 0s were also allowed?
A: Extend the logic to handle both flipping operations by maintaining separate counters for flipped 1s and 0s. Adjust the sliding window to ensure both constraints are satisfied.
Notes
Code
✅ Testcase
Input: {'k': '3', 'nums': '[1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0]'}
Expected:
10
10
Actual: -
Time: -
sec
Status: Waiting
Input: {'k': '3', 'nums': '[0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1]'}
Expected:
9
9
Actual: -
Time: -
sec
Status: Waiting
Input: {'k': '2', 'nums': '[1, 0, 0, 1, 1, 1, 0, 0, 0, 1]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting