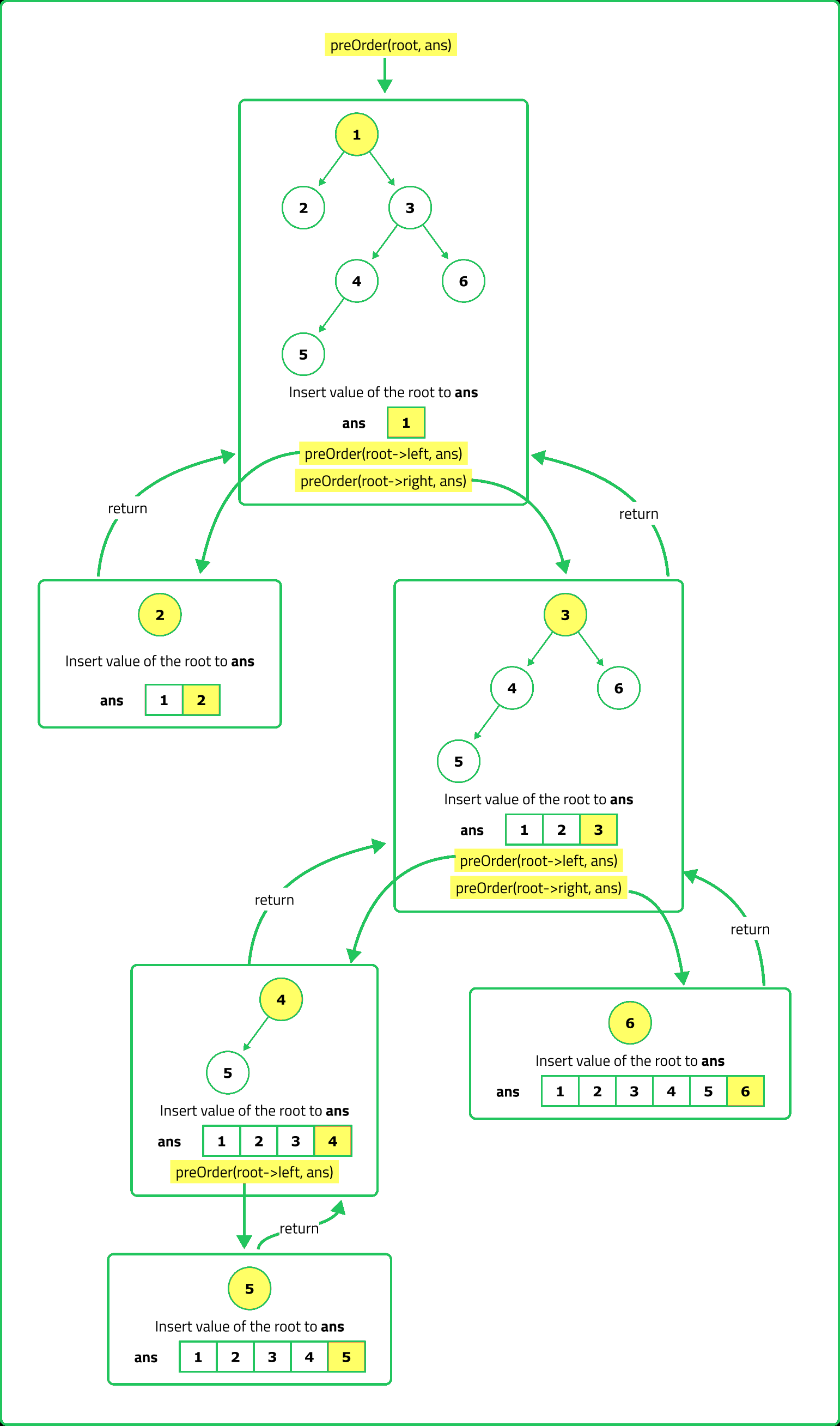
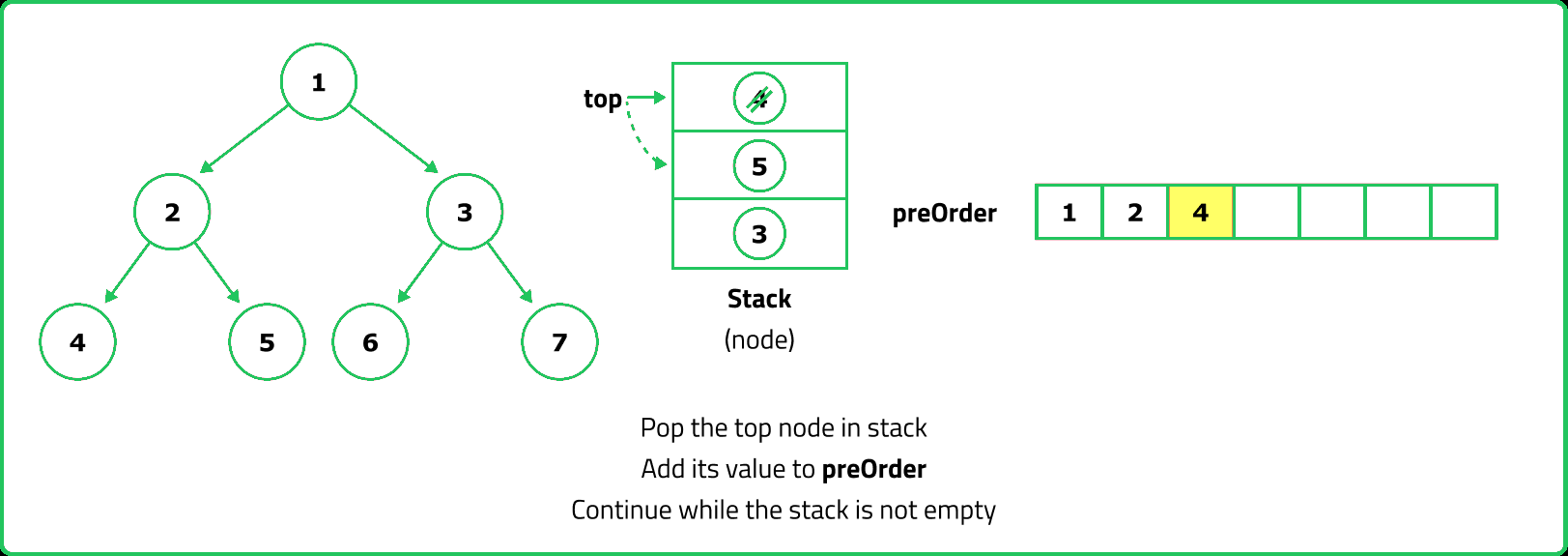
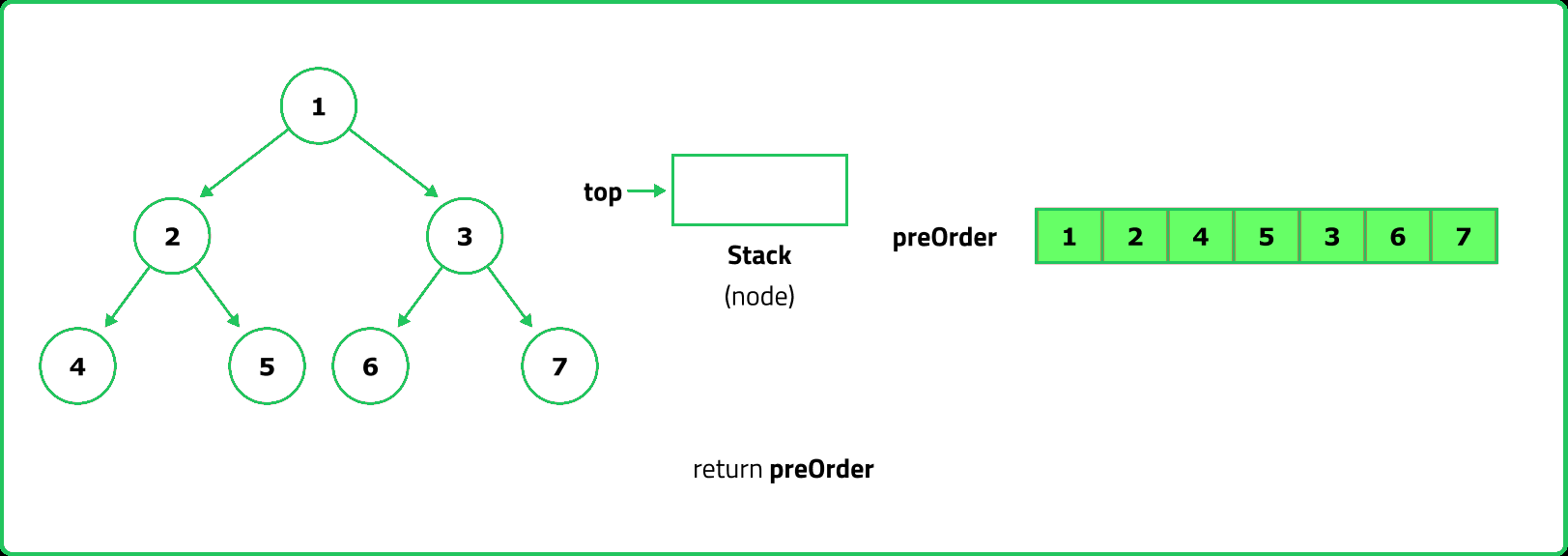
Preorder Traversal
Binary Trees
Theory/Traversals
Easy
Given root of binary tree, return the preorder traversal of the binary tree.
Examples:
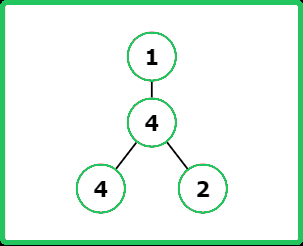
Input : root = [1, 4, null, 4 2]
Output : [1, 4, 4, 2]
Explanation :
Input : root = [1]
Output : [1]
Explanation : Only root node is present.
Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]
Constraints
- 1 <= Number of Nodes <= 100
- -100 <= Node.val <= 100
Hints
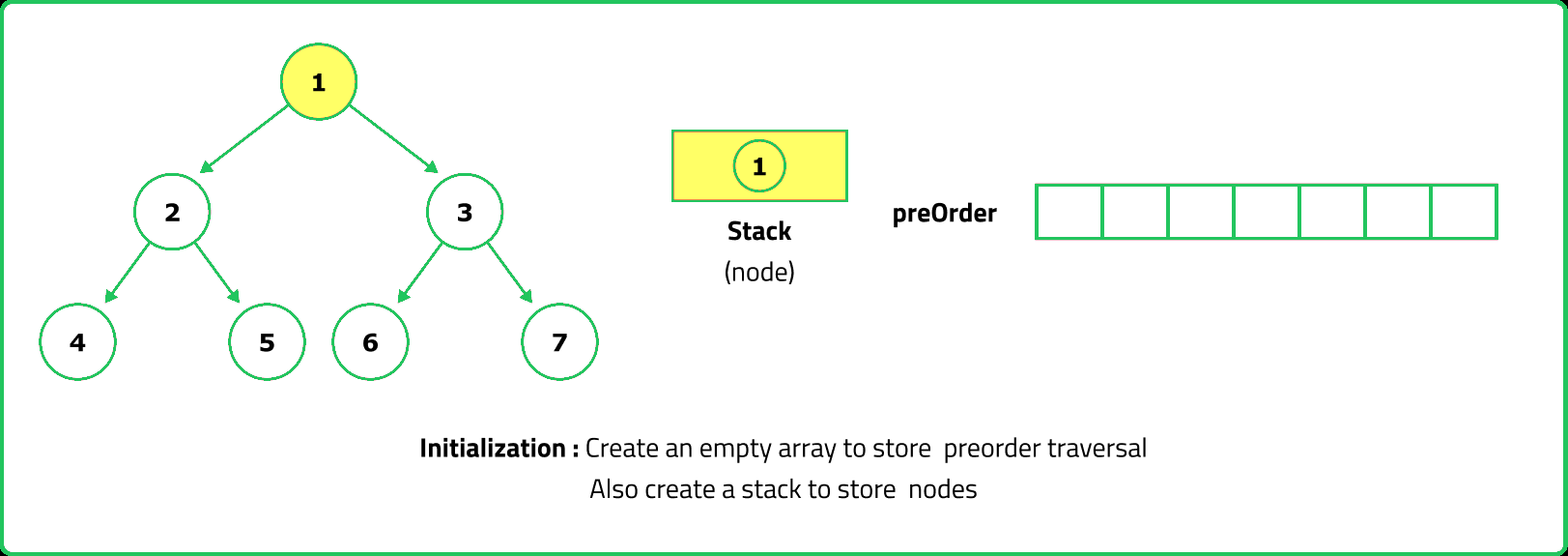
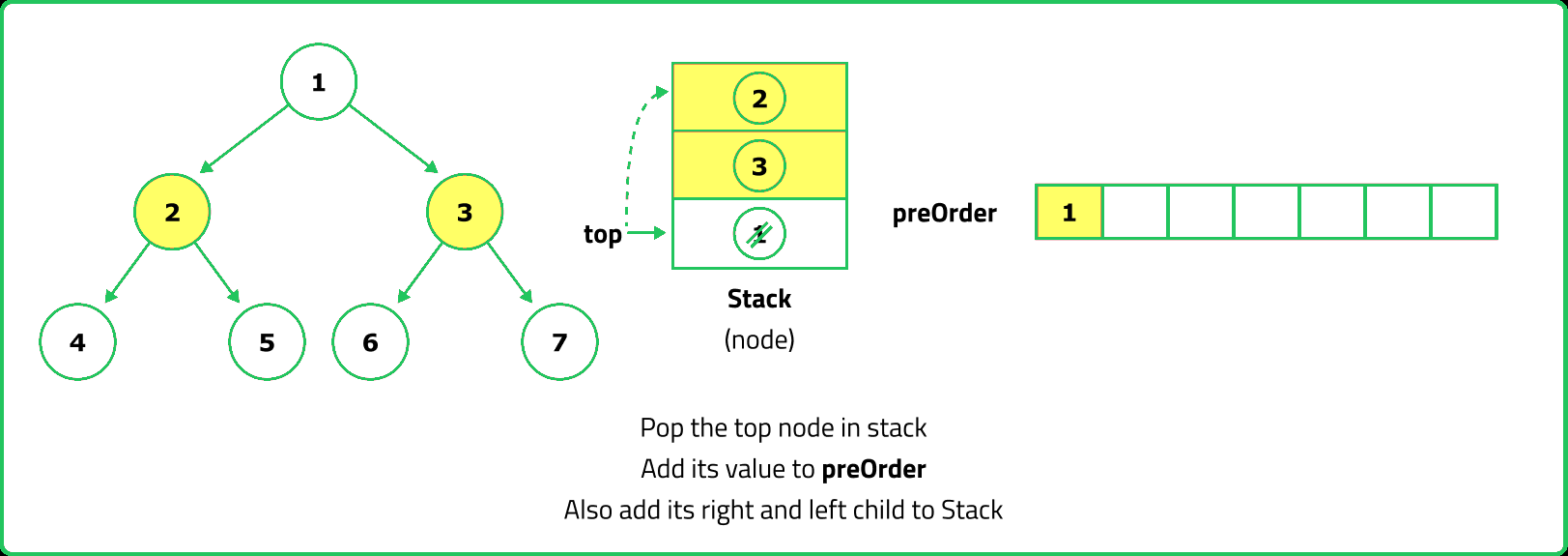
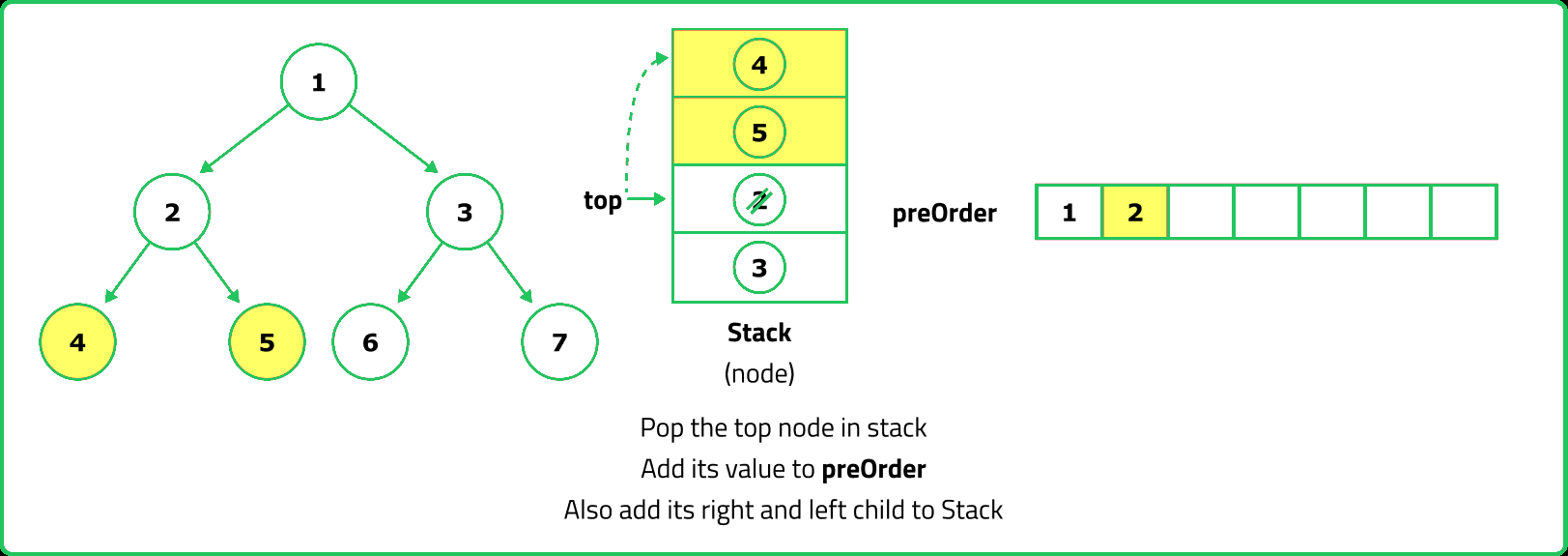
- A stack can be used to simulate recursion by manually maintaining the order of traversal. Since the traversal visits the root first, push the root onto the stack, process it, then push its right child before left (so the left is processed first).
- If the tree is empty (root is None), return an empty list. If the tree is unbalanced, the traversal should still correctly process all nodes.
Company Tags
Deloitte
Ernst & Young
Micron Technology
JPMorgan Chase
Bloomberg
Western Digital
Ubisoft
Roblox
HCL Technologies
Square
ARM
Medtronic
Uber
Target
Boston Consulting Group
Swiggy
Shopify
Chewy
Wayfair
Broadcom
Mastercard
Nutanix
Rockstar Games
Salesforce
Epic Systems
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition
Preorder traversal is one of the depth-first traversal methods used to explore nodes in a binary tree. The algorithm first visits the root node, then in the preorder traversal, we visit (i.e., add to the array) the current node by accessing its value, then we recursively traverse the left subtree in the same manner. We repeat these steps for the left subtree, then when we return to the current node, we recursively travel to the right subtree in a preorder manner as well. The sequence of steps in preorder traversal follows: Root, Left, Right.
Approach
- Base Case: If the current node is null, it means we have reached the end of a subtree and there are no further nodes to explore. Hence the recursive function stops and we return from that particular recursive call.
- Recursive Function:
- Process Current Node: The recursive function begins by processing i.e., adding to the array or printing the current node.
- Traverse Left Subtree: Recursively traverse the left subtree by invoking the preorder function on the left child of the current node. This step continues the exploration of nodes in a depth-first manner.
- Traverse Right Subtree: After traversing the entire left subtree, we traverse the right subtree recursively. We once again invoke the preorder function, but this time on the right child of the current node.
Dry Run
Algorithm:
- Step 1: Check for the base case that if the current node is null, exit the void function.
- Step 2: Push the value of the current node into the preorder traversal array.
- Step 3: Invoke the preorder function on the left child then right child to traverse the left and right subtrees in the preorder manner respectively.
This recursive approach implicitly uses the call stack to handle backtracking while exploring the tree nodes.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
// Constructor to initialize a node with a value
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Helper function to perform preorder traversal
void func(TreeNode* node, vector<int>& ans) {
// If the current node is null, return (base case for recursion)
if (node == nullptr) {
return;
}
// Append the current node's value to the list
ans.push_back(node->data);
// Recursively traverse the left subtree
func(node->left, ans);
// Recursively traverse the right subtree
func(node->right, ans);
}
// Function to initiate preorder traversal and return the resulting vector
vector<int> preorder(TreeNode* root) {
// Create an empty vector to store preorder traversal values
vector<int> ans;
// Call the helper function with the root node and the vector
func(root, ans);
// Return the resulting vector containing preorder traversal values
return ans;
}
};
// Main function to test the preorder traversal
int main() {
// Creating a sample binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// Create an instance of the Solution class
Solution solution;
// Getting preorder traversal
vector<int> result = solution.preorder(root);
// Displaying the preorder traversal result
cout << "Preorder Traversal: ";
for (int val : result) {
cout << val << " ";
}
cout << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
import java.util.ArrayList;
import java.util.List;
// Definition for a binary tree node
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
// Constructor to initialize a node with a value
TreeNode(int val) {
this.data = val;
this.left = null;
this.right = null;
}
}
class Solution {
// Helper function to perform preorder traversal
private void func(TreeNode node, List<Integer> ans) {
// If the current node is null, return (base case for recursion)
if (node == null) {
return;
}
// Append the current node's value to the list
ans.add(node.data);
// Recursively traverse the left subtree
func(node.left, ans);
// Recursively traverse the right subtree
func(node.right, ans);
}
// Function to initiate preorder traversal and return the resulting list
public List<Integer> preorder(TreeNode root) {
// Create an empty list to store preorder traversal values
List<Integer> ans = new ArrayList<>();
// Call the helper function with the root node and the list
func(root, ans);
// Return the resulting list containing preorder traversal values
return ans;
}
// Main method to test the preorder traversal
public static void main(String[] args) {
// Creating a sample binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// Create an instance of the Solution class
Solution solution = new Solution();
// Getting preorder traversal
List<Integer> result = solution.preorder(root);
// Displaying the preorder traversal result
System.out.print("Preorder Traversal: ");
for (int val : result) {
System.out.print(val + " ");
}
System.out.println();
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
# Helper function to perform preorder traversal
def func(self, node, ans):
# If the current node is None, return (base case for recursion)
if node is None:
return
# Append the current node's value to the list
ans.append(node.val)
# Recursively traverse the left subtree
self.func(node.left, ans)
# Recursively traverse the right subtree
self.func(node.right, ans)
# Function to initiate preorder traversal and return the resulting list
def preorder(self, root):
# Create an empty list to store preorder traversal values
ans = []
# Call the helper function with the root node and the list
self.func(root, ans)
# Return the resulting list containing preorder traversal values
return ans
# Main function to test the preorder traversal
if __name__ == "__main__":
# Creating a sample binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# Create an instance of the Solution class
solution = Solution()
# Getting preorder traversal
result = solution.preorder(root)
# Displaying the preorder traversal result
print("Preorder Traversal:", end=" ")
# Output each value in the preorder traversal result
for val in result:
print(val, end=" ")
print()
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
// Definition for a binary tree node
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
// Helper function to perform preorder traversal
func(node, ans) {
// If the current node is null, return (base case for recursion)
if (node === null) {
return;
}
// Append the current node's value to the list
ans.push(node.val);
// Recursively traverse the left subtree
this.func(node.left, ans);
// Recursively traverse the right subtree
this.func(node.right, ans);
}
// Function to initiate preorder traversal and return the resulting list
preorder(root) {
// Create an empty list to store preorder traversal values
const ans = [];
// Call the helper function with the root node and the list
this.func(root, ans);
// Return the resulting list containing preorder traversal values
return ans;
}
}
// Main function to test the preorder traversal
function main() {
// Creating a sample binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// Create an instance of the Solution class
const solution = new Solution();
// Getting preorder traversal
const result = solution.preorder(root);
// Displaying the preorder traversal result
console.log("Preorder Traversal:", result.join(" "));
}
// Run the main function to test the code
main();
Complexity Analysis :
Time Complexity: O(N) where N is the number of nodes in the binary tree, as each node of the binary tree is visited exactly once.
Space Complexity: O(N) where N is the number of nodes in the binary tree, as an additional space for the array is allocated to store the values of all ‘N’ nodes of the binary tree.
Intuition
As a prerequisite to this approach, please understand Preorder Traversal in detail. The preorder traversal of a Binary Tree follows the order: Root, Left then Right. An iterative approach maintains a stack structure to simulate the recursive nature of the traversal without using actual recursion. The stack follows a last-in-first-out methodology and stores the nodes yet to be processed mimicking the depth-first search characteristic of preorder traversal.
Approach
- Initially, the root node is pushed into the stack. While the stack is not empty, we continuously pop nodes from the stack and for each popped node, we add its value to the resultant traversal vector, push its right child onto the stack followed by its left child.
- This sequence ensures that the left child, which should be processed first in the preorder traversal, is visited before the right child due to the Last In, First Out behaviour of the stack. This process continues until all nodes are processed.
Dry Run
Algorithm:
- Step 1: Initialise an empty vector ‘preorder’ to store the preorder traversal result. Create a stack to store the nodes during traversal and push the root node onto the stack. Check if the root is null, return an empty traversal result if true.
- Step 2: Push the root of the binary tree into the stack.
-
Step 3: While the stack is not empty:
- Get the current node from the top of the stack.
- Remove the node from the stack.
- Add the node’s value to the preorder traversal result.
- First, push the right child onto the stack if it exists.
- Secondly, push the left child onto the stack if it exists.
- Step 4: Return the ‘preorder’ traversal result.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
#include <bits/stdc++.h>
using namespace std;
// Define the TreeNode structure
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to perform preorder traversal
// of a binary tree iteratively
vector<int> preorder(TreeNode* root) {
// Initialize vector to store
// the preorder traversal result
vector<int> preorder;
// If the root is null, return
// an empty traversal result
if(root == nullptr) {
return preorder;
}
// Create a stack to store
// nodes during traversal
stack<TreeNode*> st;
// Push the root node
// onto the stack
st.push(root);
// Perform iterative preorder traversal
while(!st.empty()) {
// Get the current node
// from the top of the stack
root = st.top();
// Remove the node
// from the stack
st.pop();
// Add the node's value to
// the preorder traversal result
preorder.push_back(root->data);
// Push the right child
// onto the stack if exists
if(root->right != nullptr) {
st.push(root->right);
}
// Push the left child onto
// the stack if exists
if(root->left != nullptr) {
st.push(root->left);
}
}
// Return the preorder
// traversal result
return preorder;
}
};
int main() {
// Creating a binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// Initializing the Solution class
Solution sol;
// Getting the preorder traversal
vector<int> result = sol.preorder(root);
// Displaying the preorder traversal result
cout << "Preorder Traversal: ";
for (int val : result) {
cout << val << " ";
}
cout << endl;
return 0;
}1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889
import java.util.*;
// Define the TreeNode structure
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int x) {
data = x;
left = null;
right = null;
}
}
class Solution {
// Function to perform preorder traversal
// of a binary tree iteratively
public List<Integer> preorder(TreeNode root) {
// Initialize list to store
// the preorder traversal result
List<Integer> preorder = new ArrayList<>();
// If the root is null, return
// an empty traversal result
if (root == null) {
return preorder;
}
// Create a stack to store
// nodes during traversal
Stack<TreeNode> st = new Stack<>();
// Push the root node
// onto the stack
st.push(root);
// Perform iterative preorder traversal
while (!st.empty()) {
// Get the current node
// from the top of the stack
root = st.pop();
// Add the node's value to
// the preorder traversal result
preorder.add(root.data);
// Push the right child
// onto the stack if exists
if (root.right != null) {
st.push(root.right);
}
// Push the left child onto
// the stack if exists
if (root.left != null) {
st.push(root.left);
}
}
// Return the preorder
// traversal result
return preorder;
}
}
public class Main {
public static void main(String[] args) {
// Creating a binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// Initializing the Solution class
Solution sol = new Solution();
// Getting the preorder traversal
List<Integer> result = sol.preorder(root);
// Displaying the preorder traversal result
System.out.print("Preorder Traversal: ");
for (int val : result) {
System.out.print(val + " ");
}
System.out.println();
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
from typing import List
# Define the TreeNode structure
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
# Function to perform preorder traversal
# of a binary tree iteratively
def preorder(self, root: TreeNode) -> List[int]:
# Initialize list to store
# the preorder traversal result
preorder = []
# If the root is None, return
# an empty traversal result
if root is None:
return preorder
# Create a stack to store
# nodes during traversal
st = []
# Push the root node
# onto the stack
st.append(root)
# Perform iterative preorder traversal
while st:
# Get the current node
# from the top of the stack
root = st.pop()
# Add the node's value to
# the preorder traversal result
preorder.append(root.val)
# Push the right child
# onto the stack if exists
if root.right:
st.append(root.right)
# Push the left child onto
# the stack if exists
if root.left:
st.append(root.left)
# Return the preorder
# traversal result
return preorder
# Creating a binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# Initializing the Solution class
sol = Solution()
# Getting the preorder traversal
result = sol.preorder(root)
# Displaying the preorder traversal result
print("Preorder Traversal:", end=" ")
for val in result:
print(val, end=" ")
print()
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
class TreeNode {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
class Solution {
// Function to perform preorder traversal
// of a binary tree iteratively
preorder(root) {
// Initialize array to store
// the preorder traversal result
let preorder = [];
// If the root is null, return
// an empty traversal result
if (root === null) {
return preorder;
}
// Create a stack to store
// nodes during traversal
let stack = [];
// Push the root node
// onto the stack
stack.push(root);
// Perform iterative preorder traversal
while (stack.length > 0) {
// Get the current node
// from the top of the stack
root = stack.pop();
// Add the node's value to
// the preorder traversal result
preorder.push(root.data);
// Push the right child
// onto the stack if exists
if (root.right !== null) {
stack.push(root.right);
}
// Push the left child onto
// the stack if exists
if (root.left !== null) {
stack.push(root.left);
}
}
// Return the preorder
// traversal result
return preorder;
}
}
// Creating a binary tree
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// Initializing the Solution class
let sol = new Solution();
// Getting the preorder traversal
let result = sol.preorder(root);
// Displaying the preorder traversal result
console.log("Preorder Traversal: " + result.join(" "));
Complexity Analysis :
Time Complexity: O(N) where N is the number of nodes in the binary tree. Every node of the binary tree is visited exactly once, and for each node, the operations performed (pushing and popping from the stack, accessing node values, etc.) are constant time operations.
Space Complexity: O(N) where N is the number of nodes in the binary tree. This is because the stack can potentially hold all nodes in the tree when dealing with a skewed tree (all nodes have only one child), consuming space proportional to the number of nodes. In the average case or for a balanced tree, the maximum number of nodes that could be in the stack at any given time would be roughly the height of the tree, hence O(log2N).
Frequently Occurring Doubts
Q: Why is preorder traversal useful?
A: Preorder is commonly used for creating copies of trees, serializing structures, and constructing expressions in syntax trees.
Q: How does an iterative approach maintain the traversal order?
A: The stack ensures that the left subtree is processed first by pushing the right child before the left child.
Interview Followup Questions
Q: How would you modify this traversal for an n-ary tree?
A: Instead of just left and right, iterate over all children in the correct order using a stack or recursion.
Q: How would you traverse the tree in a depth-first search (DFS) manner?
A: Preorder itself is a DFS traversal, but can be modified for inorder and postorder as well.
Notes
Code
✅ Testcase
Input: {'s': '1 4 null 4 2'}
Expected:
1 4 4 2
1 4 4 2
Actual: -
Time: -
sec
Status: Waiting
Input: {'s': '1'}
Expected:
1
1
Actual: -
Time: -
sec
Status: Waiting
Input: {'s': '1 2 3 5 8 9'}
Expected:
1 2 5 8 3 9
1 2 5 8 3 9
Actual: -
Time: -
sec
Status: Waiting
Facts
- • Fun Fact: Preorder traversal of a binary tree is a classic algorithm often used in practical software development
- • For instance, in areas involving hierarchical datasets, such as the DOM (Document Object Model) in web development
- • In this context, each HTML/XML tag can be seen as a node in a tree with a hierarchical structure
- • Preorder traversal is then used to traverse the entire DOM in an orderly manner, allowing developers to effectively manipulate, add, or remove elements