Detect a cycle in an undirected graph
Graphs
Cycles
Hard
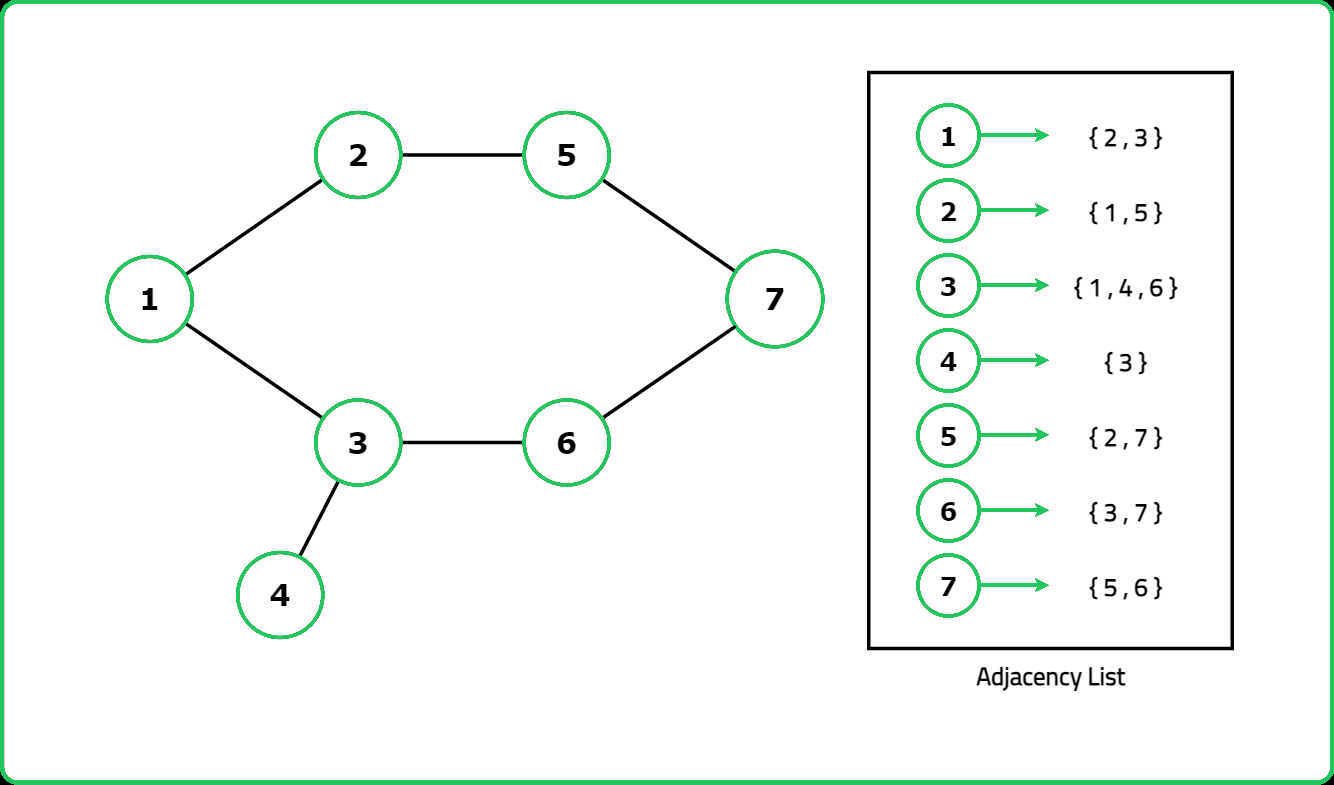
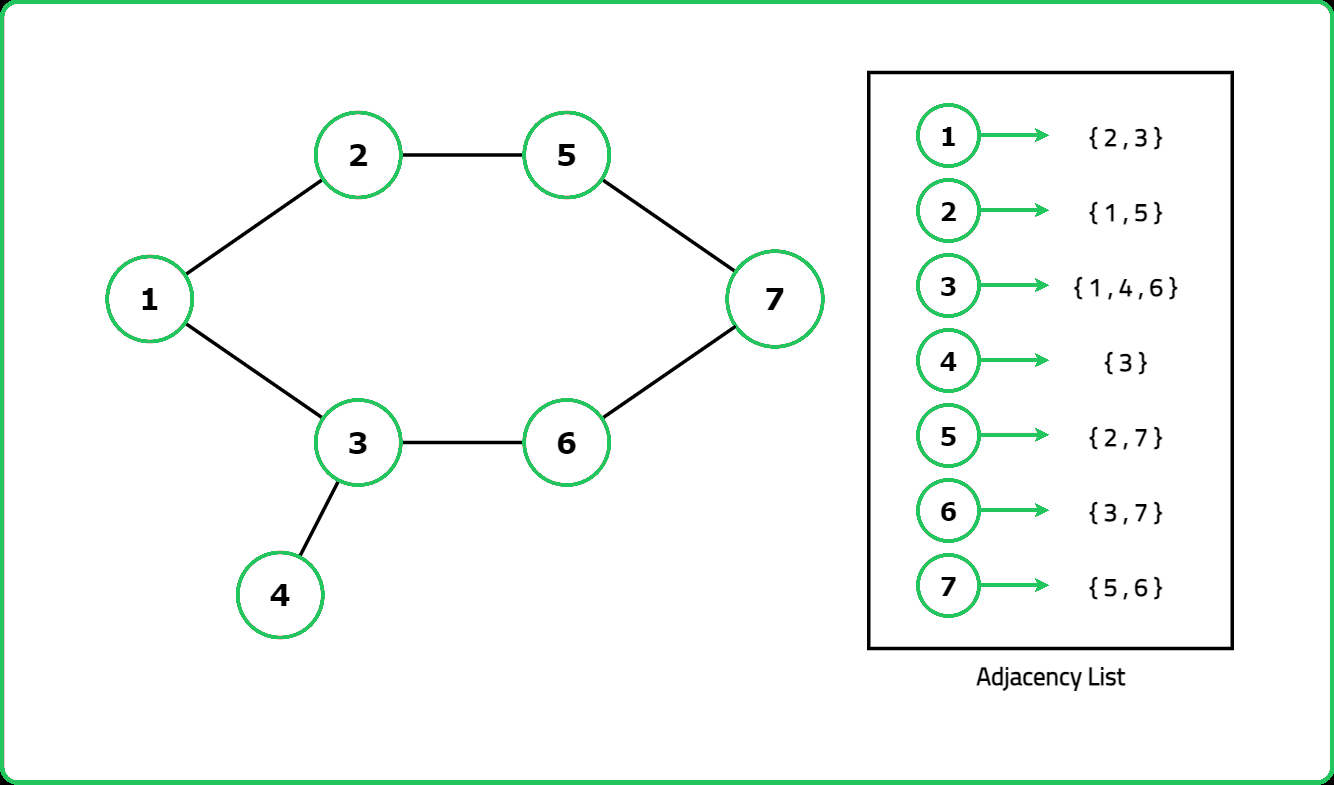
Given an undirected graph with V vertices labeled from 0 to V-1. The graph is represented using an adjacency list where adj[i] lists all nodes connected to node. Determine if the graph contains any cycles.
Note: The graph does not contain any self-edges (edges where a vertex is connected to itself).
Examples:
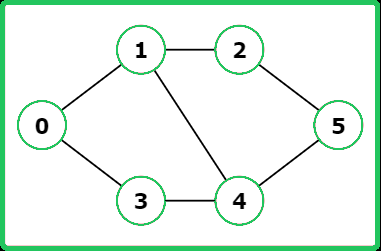
Input: V = 6, adj= [[1, 3], [0, 2, 4], [1, 5], [0, 4], [1, 3, 5], [2, 4]]
Output: True
Explanation: The graph contains a cycle: 0 ->1 -> 2 -> 5 -> 4 -> 1.
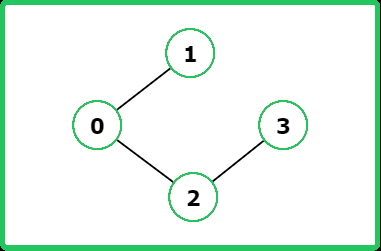
Input: V = 4, adj= [[1, 2], [0], [0, 3], [2]]
Output: False
Explanation: The graph does not contain any cycles.
Input: V = 4, adj= [[1, 2], [0, 2], [0, 1, 3], [2]]
Constraints
- E=number of edges
- 1 ≤ V, E ≤ 104
Hints
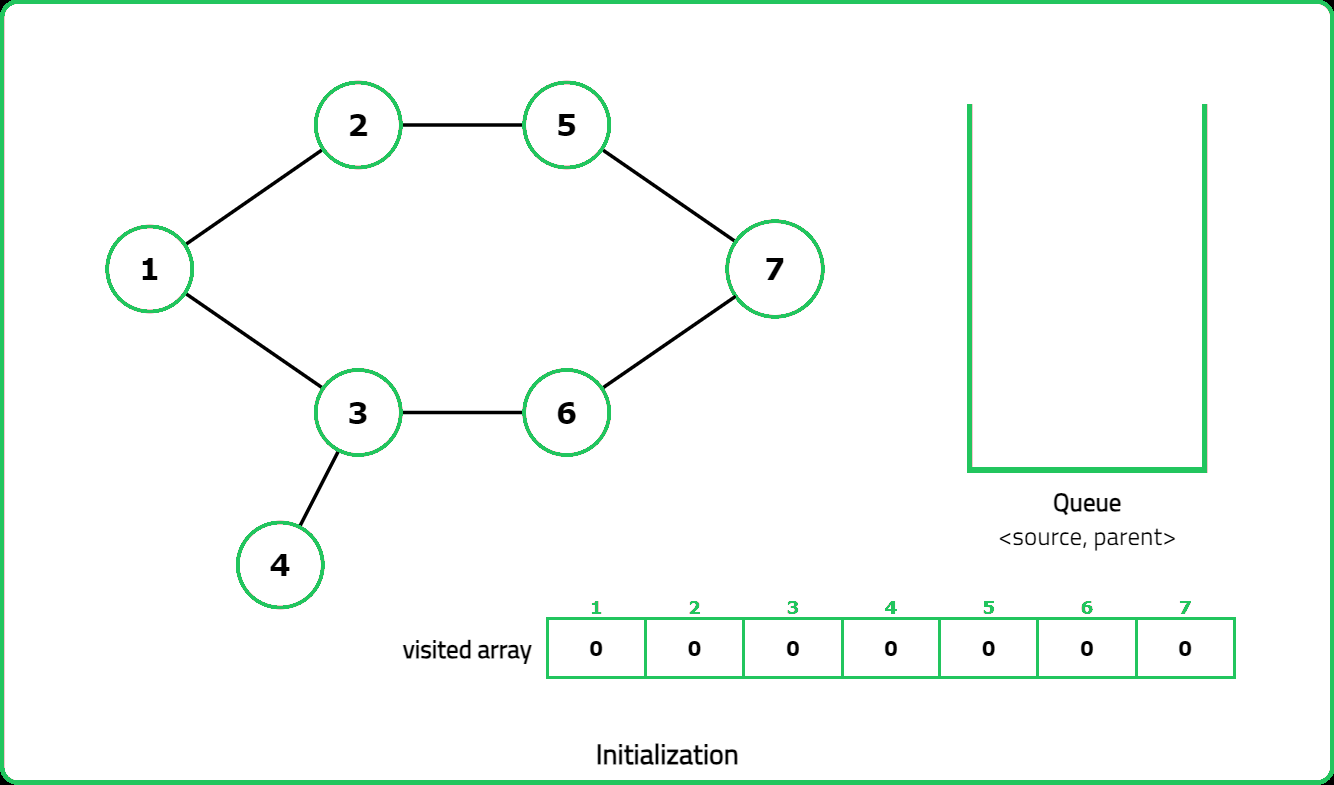
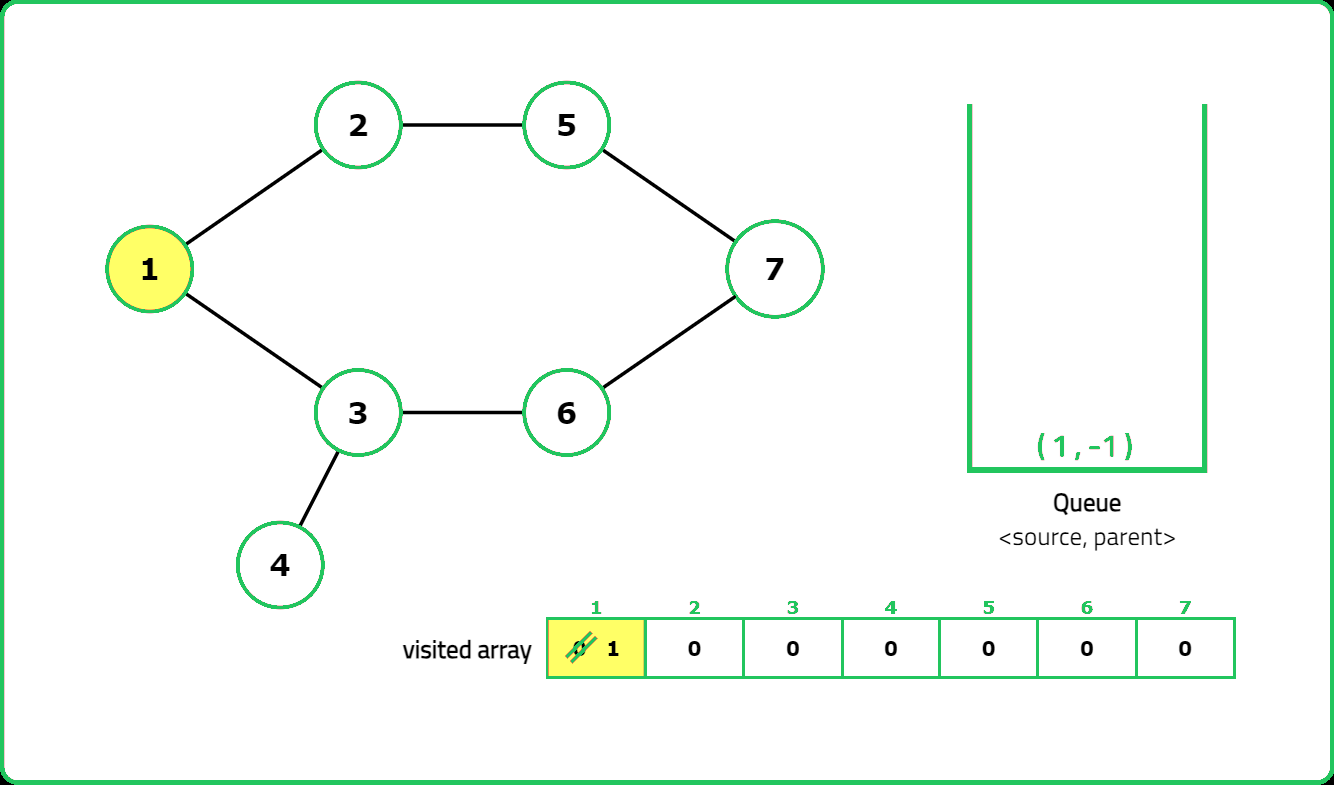
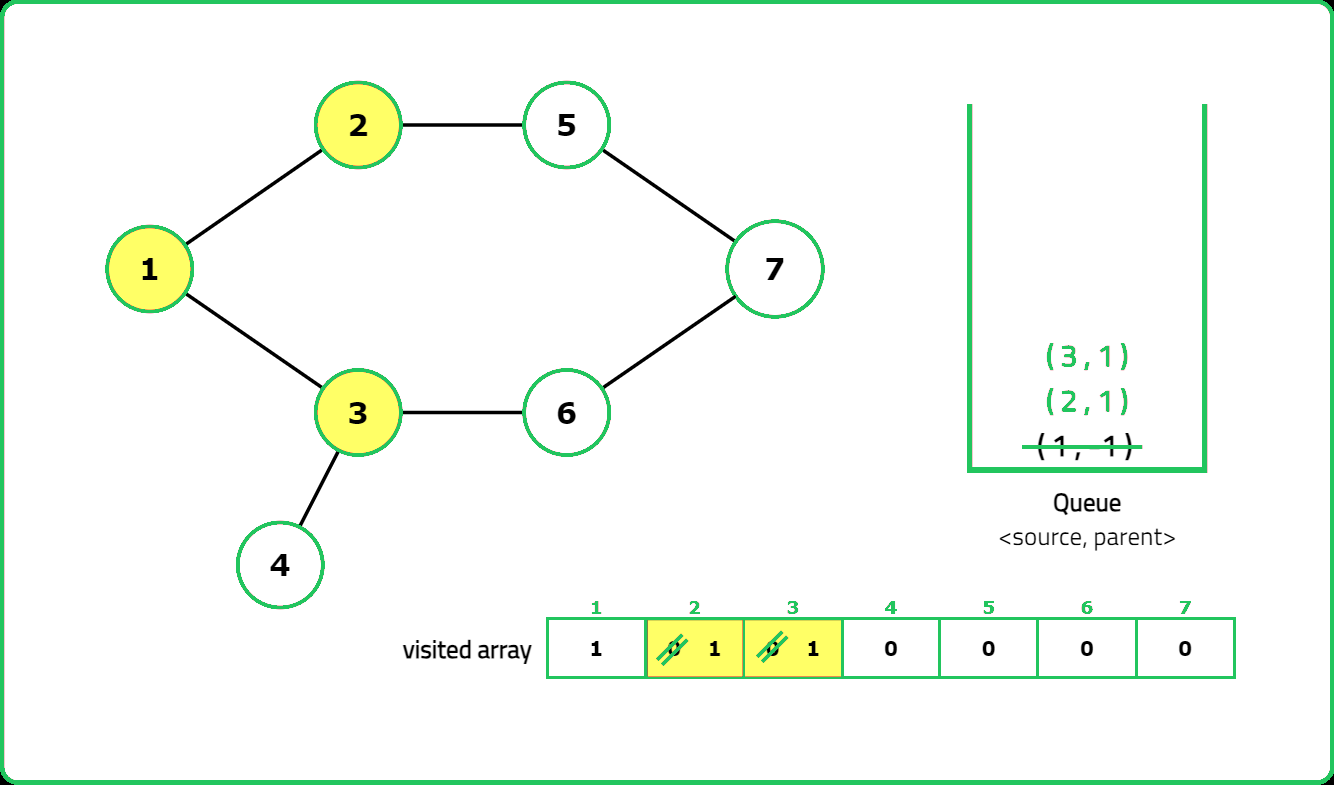
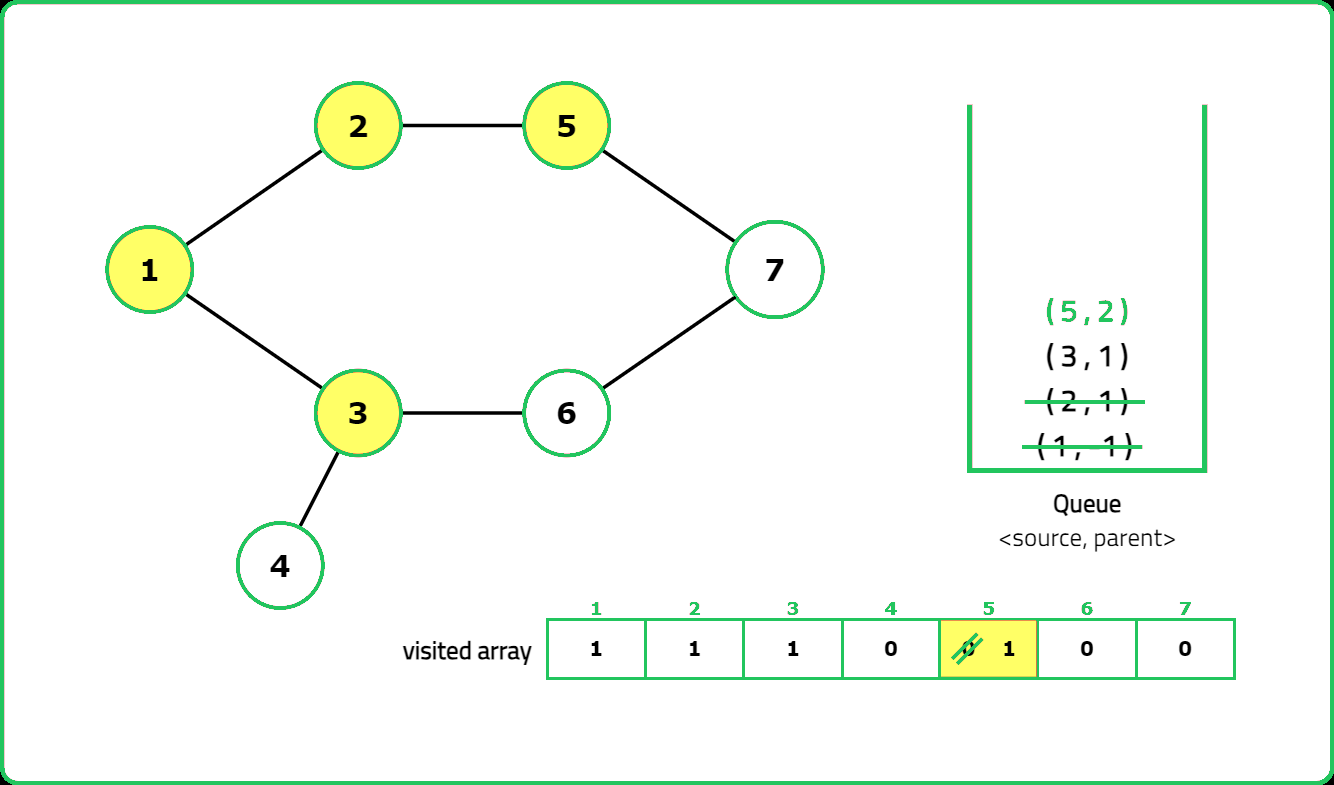
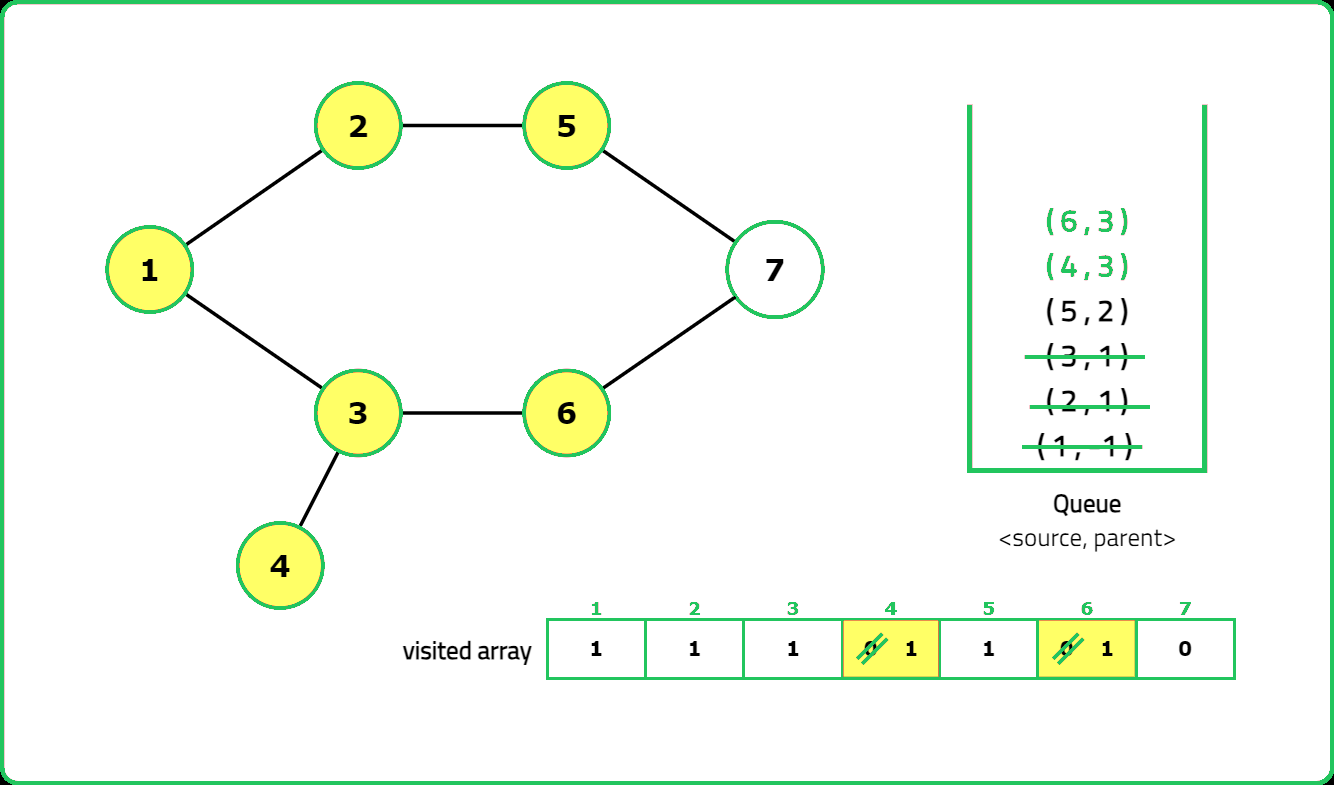
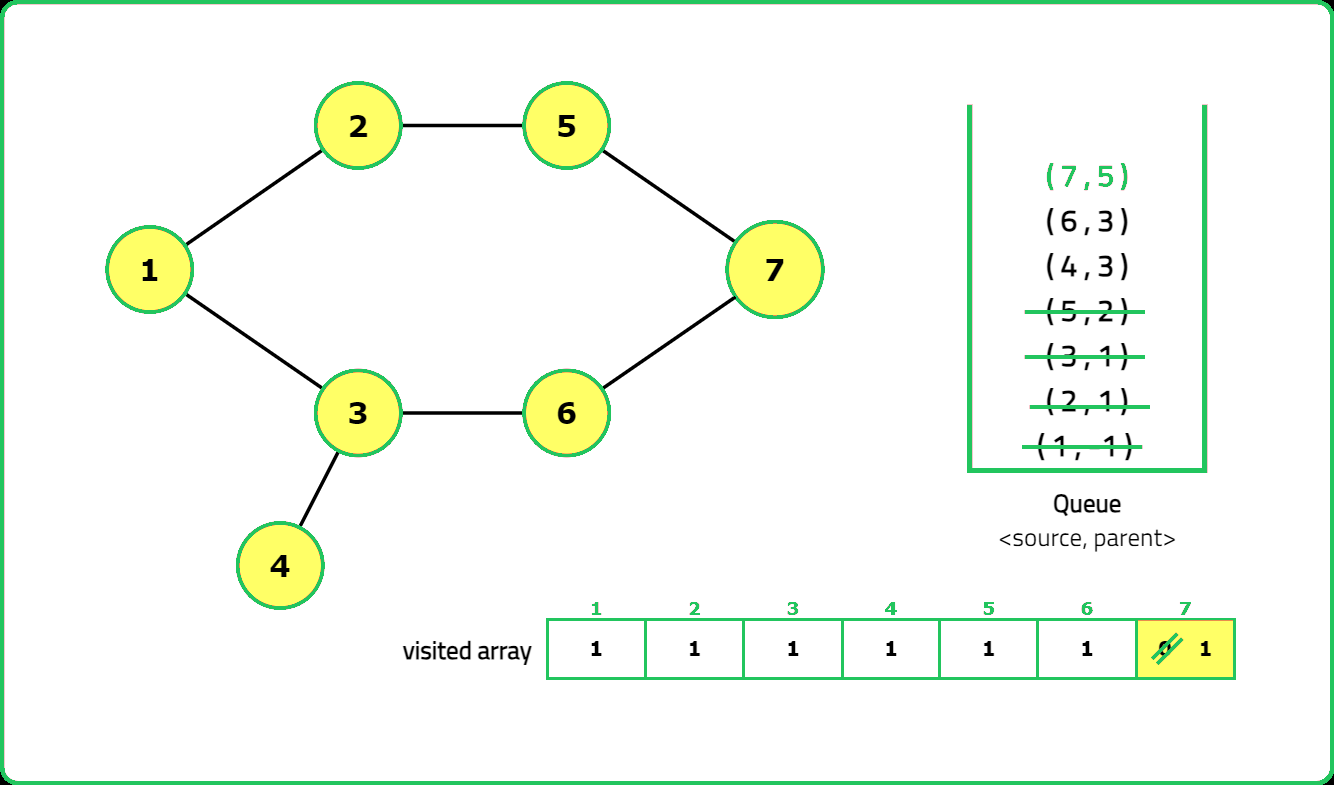
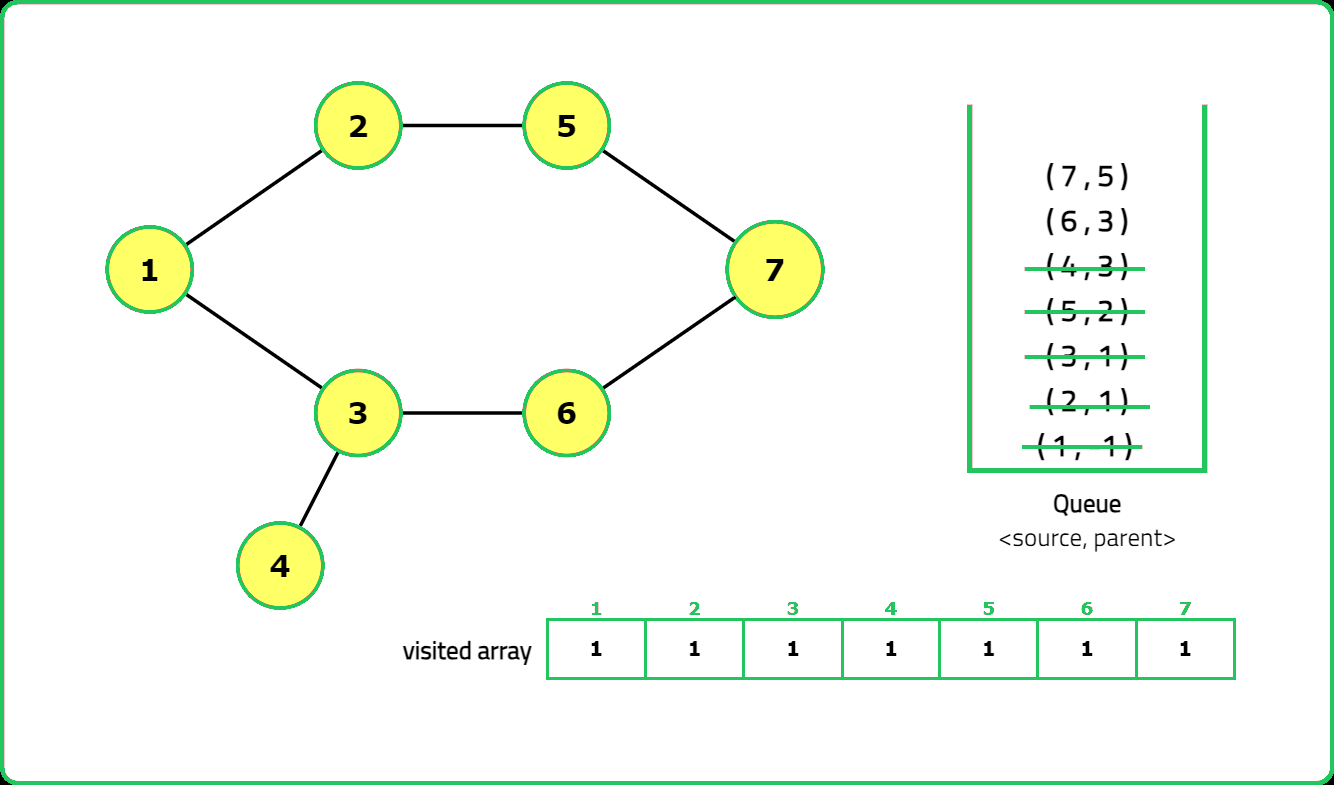
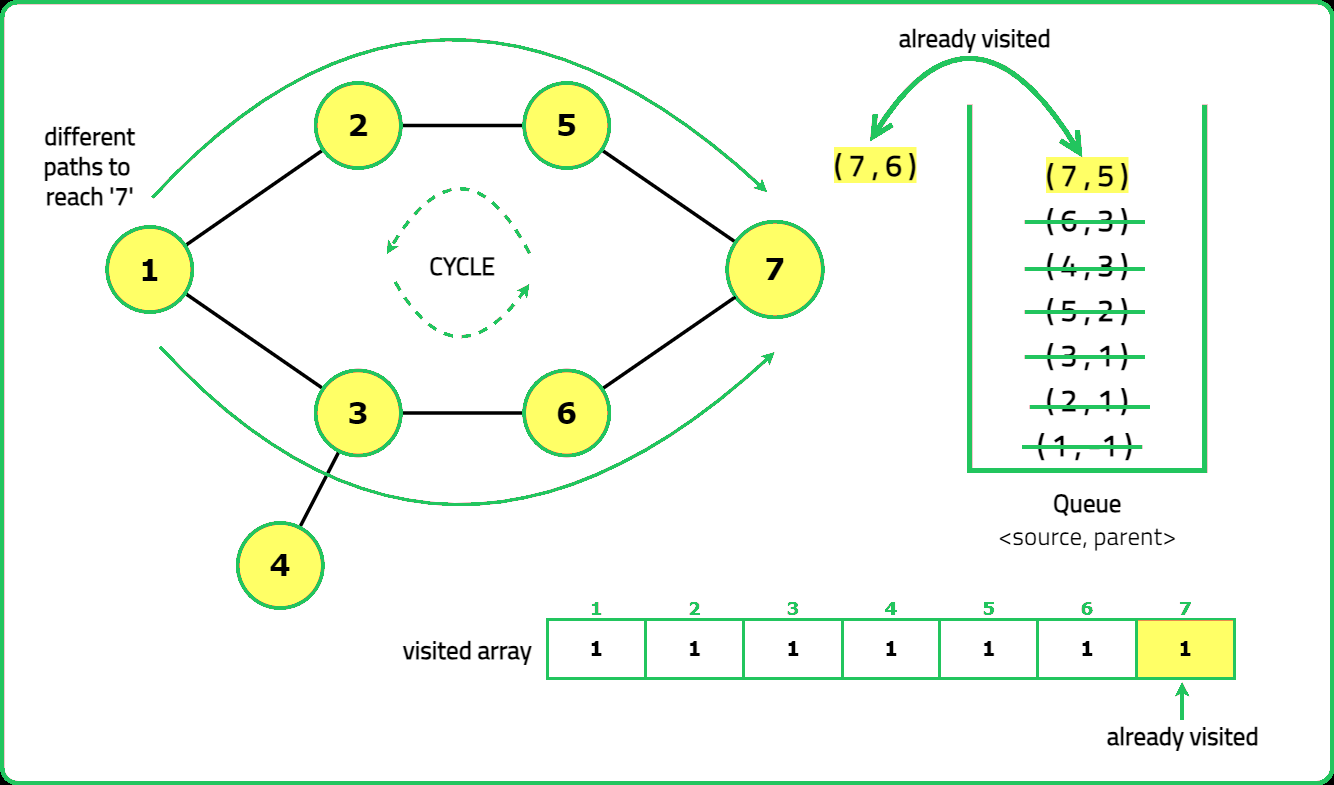
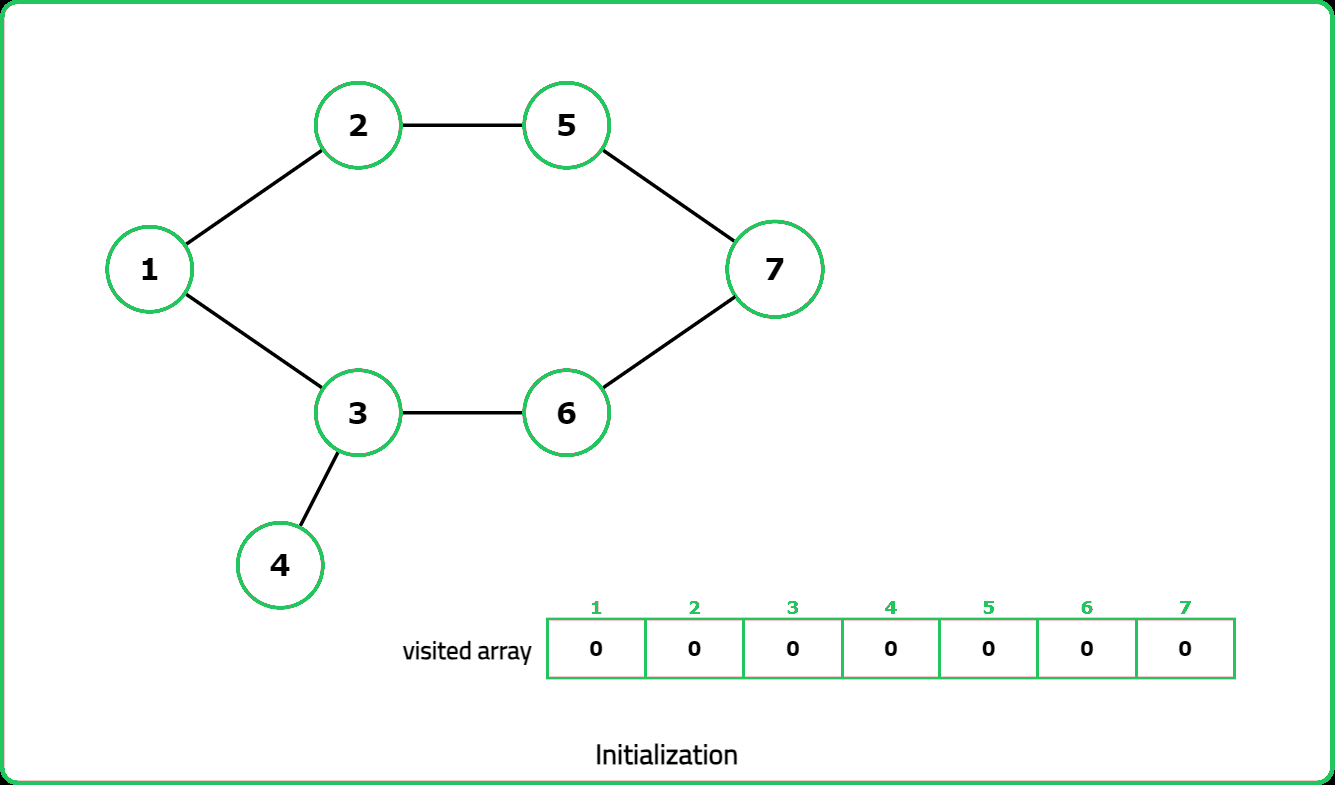
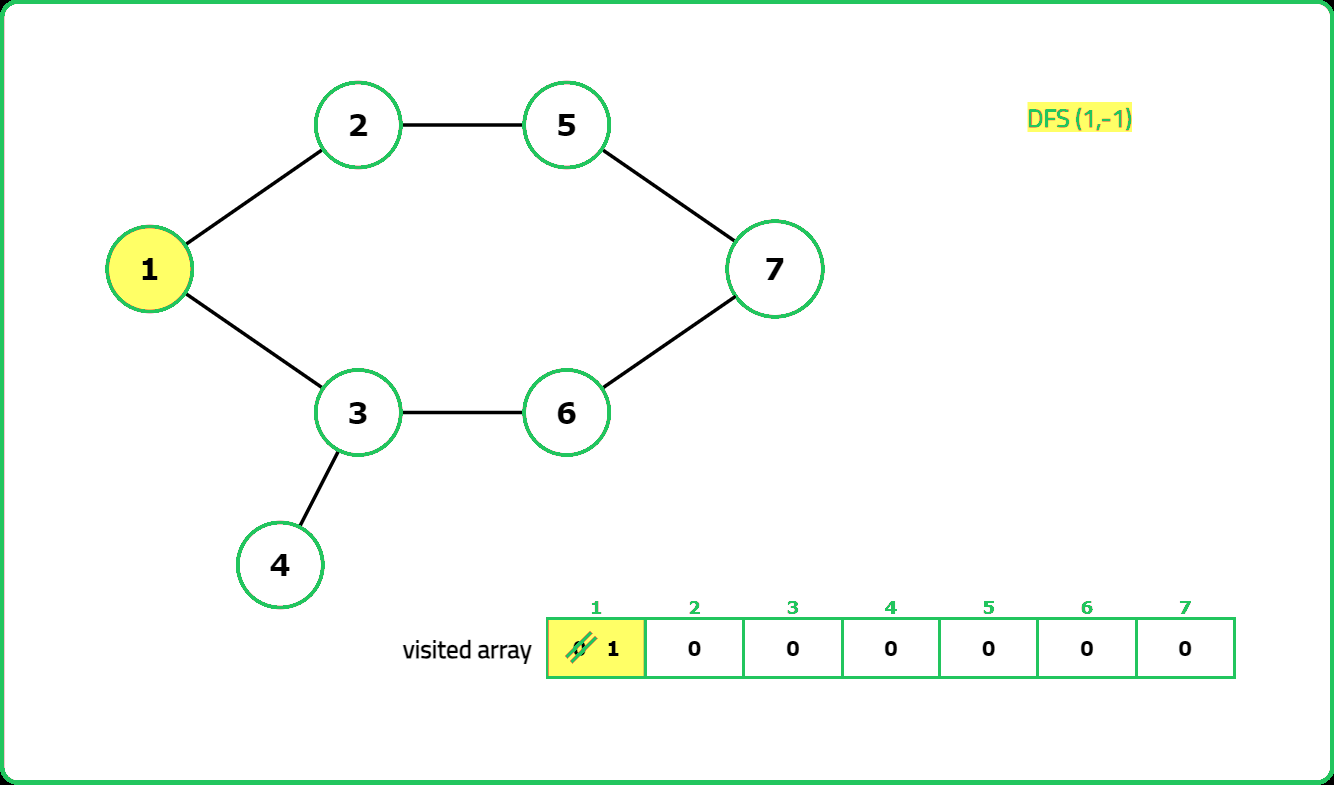
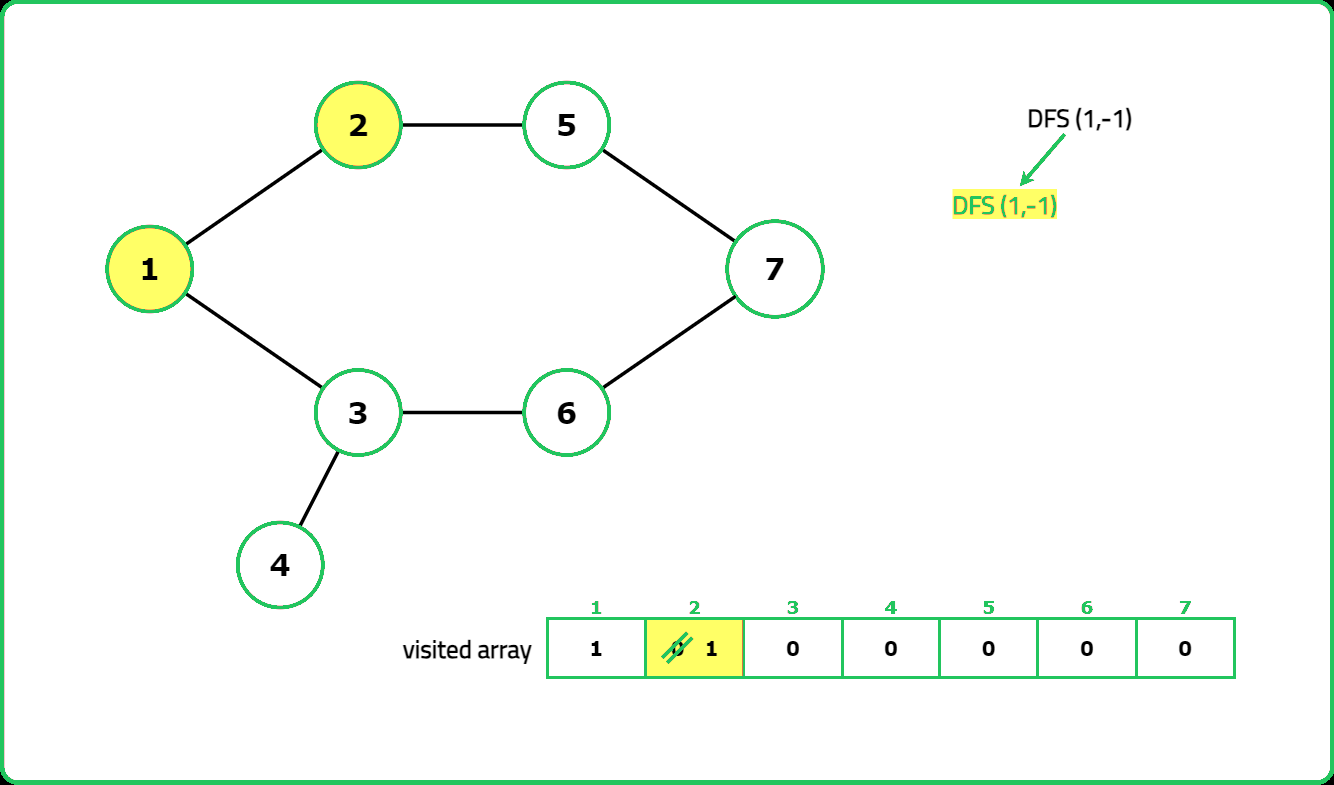
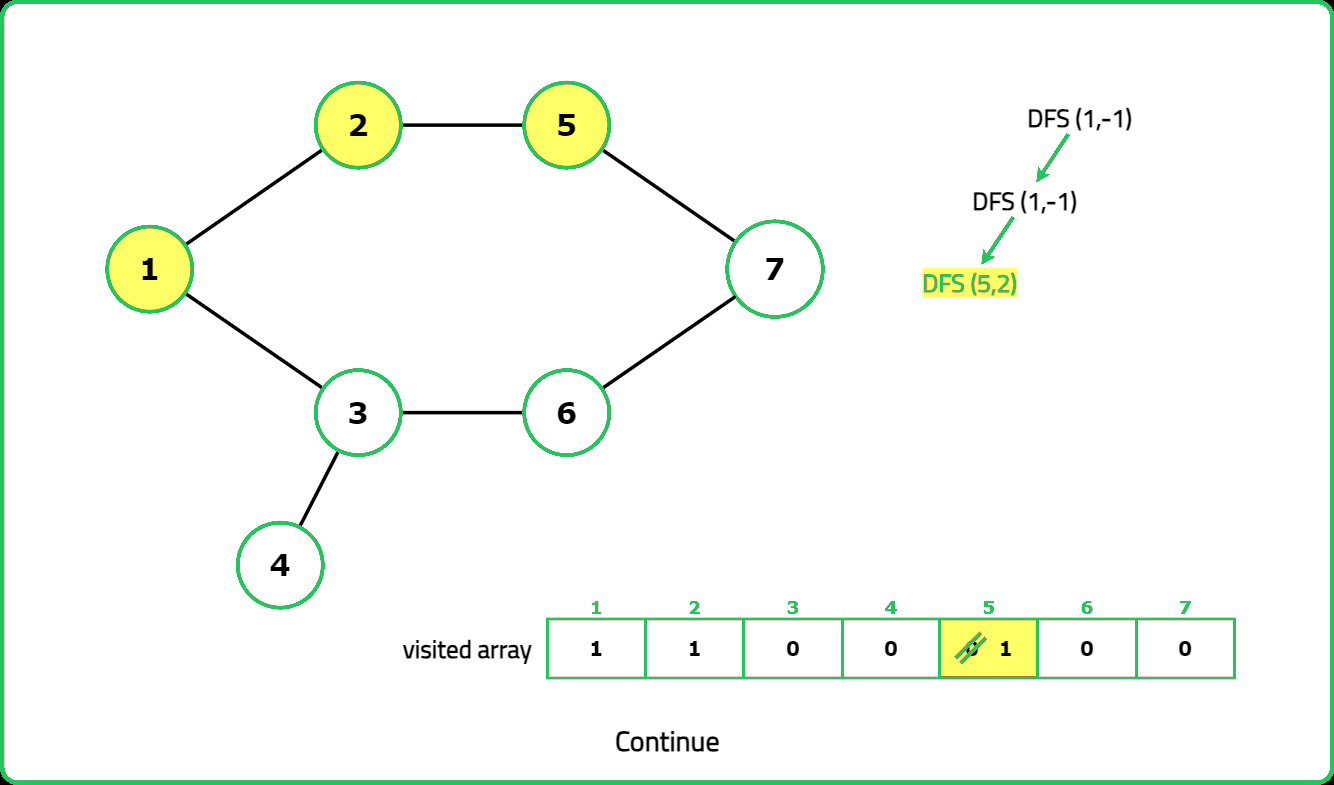
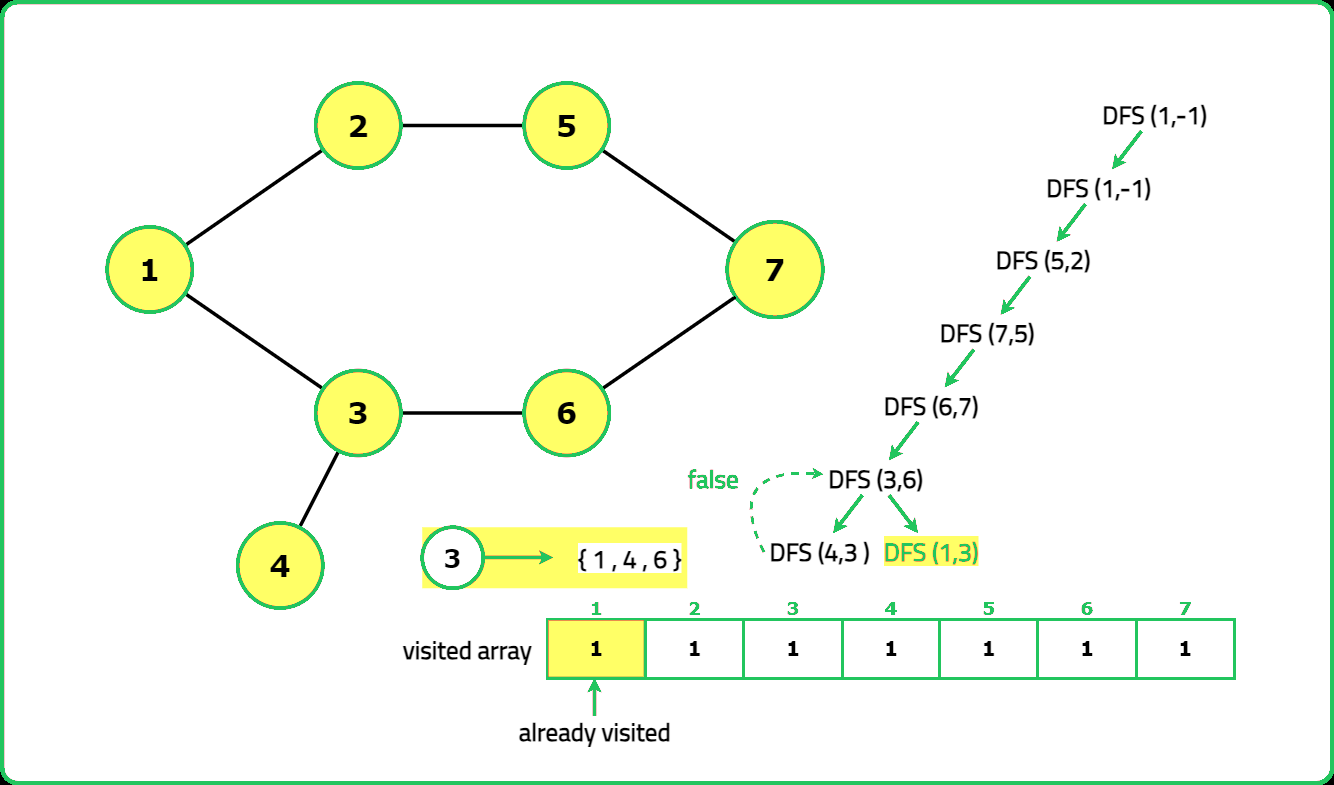
- "Use DFS with a visited array to track traversal. A cycle exists if a visited node is reached again and it is not the parent node."
- "Use Union-Find to track connected components. If an edge connects two nodes already in the same set, a cycle is detected."
Company Tags
DoorDash
Databricks
Shopify
Intel
Bloomberg
Epic Games
Western Digital
Instacart
Mastercard
Johnson & Johnson
Reddit
Ubisoft
Wayfair
HashiCorp
Deloitte
Morgan Stanley
Zynga
Etsy
Broadcom
Boston Consulting Group
Goldman Sachs
Robinhood
Square
Electronic Arts
Walmart
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
In an undirected graph, a cycle is formed when a path exists that returns to the starting vertex without reusing an edge. The key idea is that during traversal (e.g., using Breadth-First Search (BFS) for this approach), if we encounter a vertex that has already been visited and is not the immediate parent of the current vertex, a cycle exists.
Approach:
- A helper function performs BFS to detect cycles, using a queue to track nodes and their parents. For each unvisited node, initialize the queue with the node and mark it as visited.
- While the queue is not empty, process each node's neighbors:
- If a neighbor is unvisited, mark it visited and enqueue it.
- If a neighbor is visited and not the parent, a cycle is detected.
- Return true if any cycle is found during traversal.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to perform BFS traversal
bool bfs(int i, vector<int> adj[],
vector<bool> &visited) {
// Queue to store {node, parent}
queue<pair<int, int>> q;
/* Push initial node in queue
with no one as parent */
q.push({i, -1});
// Mark the node as visited
visited[i] = true;
// Until the queue is empty
while(!q.empty()) {
// Get the node and its parent
int node = q.front().first;
int parent = q.front().second;
q.pop();
// Traverse all the neighbors
for(auto it : adj[node]) {
// If not visited
if(!visited[it]) {
// Mark the node as visited
visited[it] = true;
/* Push the new node in queue
with curr node as parent */
q.push({it, node});
}
/* Else if it is visited with some
different parent a cycle is detected */
else if(it != parent) return true;
}
}
return false;
}
public:
// Function to detect cycle in an undirected graph.
bool isCycle(int V, vector<int> adj[]) {
// Visited array
vector<bool> visited(V, false);
/* Variable to store if
there is a cycle detected */
bool ans = false;
// Start Traversal from every unvisited node
for(int i=0; i<V; i++) {
if(!visited[i]) {
// Start BFS traversal and update result
ans = bfs(i, adj, visited);
// Break if a cycle is detected
if(ans) break;
}
}
return ans;
}
};
int main() {
int V = 6;
vector<int> adj[V] = {
{1, 3},
{0, 2, 4},
{1, 5},
{0, 4},
{1, 3, 5},
{2, 4}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to detect
cycle in given graph. */
bool ans = sol.isCycle(V, adj);
// Output
if(ans)
cout << "The given graph contains a cycle.";
else
cout << "The given graph does not contain a cycle.";
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101
import java.util.*;
class Solution {
// Function to perform BFS traversal
private boolean bfs(int i,
List<Integer> adj[],
boolean[] visited) {
// Queue to store {node, parent}
Queue<int[]> q = new LinkedList<>();
/* Push initial node in queue
with no one as parent */
q.add(new int[]{i, -1});
// Mark the node as visited
visited[i] = true;
// Until the queue is empty
while (!q.isEmpty()) {
// Get the node and its parent
int[] current = q.poll();
int node = current[0];
int parent = current[1];
// Traverse all the neighbors
for (int it : adj[node]) {
// If not visited
if (!visited[it]) {
// Mark the node as visited
visited[it] = true;
/* Push the new node in queue
with curr node as parent */
q.add(new int[]{it, node});
}
/* Else if it is visited with some
different parent a cycle is detected */
else if (it != parent) return true;
}
}
return false;
}
/* Function to detect cycle
in an undirected graph. */
public boolean isCycle(int V,
List<Integer> adj[]) {
// Visited array
boolean[] visited = new boolean[V];
/* Variable to store if
there is a cycle detected */
boolean ans = false;
// Start Traversal from every unvisited node
for (int i = 0; i < V; i++) {
if (!visited[i]) {
// Start BFS traversal and update result
ans = bfs(i, adj, visited);
// Break if a cycle is detected
if (ans) break;
}
}
return ans;
}
public static void main(String[] args) {
int V = 6;
List<Integer> adj[] = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
adj[0].addAll(Arrays.asList(1, 3));
adj[1].addAll(Arrays.asList(0, 2, 4));
adj[2].addAll(Arrays.asList(1, 5));
adj[3].addAll(Arrays.asList(0, 4));
adj[4].addAll(Arrays.asList(1, 3, 5));
adj[5].addAll(Arrays.asList(2, 4));
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to detect cycle in given graph.
boolean ans = sol.isCycle(V, adj);
// Output
if (ans)
System.out.println("The given graph contains a cycle.");
else
System.out.println("The given graph does not contain a cycle.");
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
from collections import deque
class Solution:
# Function to perform BFS traversal
def bfs(self, i, adj, visited):
# Queue to store (node, parent)
q = deque()
# Push initial node in queue
# with no one as parent
q.append((i, -1))
# Mark the node as visited
visited[i] = True
# Until the queue is empty
while q:
# Get the node and its parent
node, parent = q.popleft()
# Traverse all the neighbors
for it in adj[node]:
# If not visited
if not visited[it]:
# Mark the node as visited
visited[it] = True
# Push the new node in queue
# with curr node as parent
q.append((it, node))
# Else if it is visited with some
# different parent a cycle is detected
elif it != parent:
return True
return False
# Function to detect cycle in an undirected graph.
def isCycle(self, V, adj):
visited = [False] * V
ans = False
# Start Traversal from every unvisited node
for i in range(V):
if not visited[i]:
# Start BFS traversal and update result
ans = self.bfs(i, adj, visited)
# Break if a cycle is detected
if ans:
break
return ans
if __name__ == "__main__":
V = 6
adj = [
[1, 3],
[0, 2, 4],
[1, 5],
[0, 4],
[1, 3, 5],
[2, 4]
]
# Creating an instance of Solution class
sol = Solution()
# Function call to detect cycle in given graph.
ans = sol.isCycle(V, adj)
# Output
if ans:
print("The given graph contains a cycle.")
else:
print("The given graph does not contain a cycle.")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980
class Solution {
// Function to perform BFS traversal
bfs(i, adj, visited) {
// Queue to store {node, parent}
let q = [];
// Push initial node in queue with no one as parent
q.push([i, -1]);
// Mark the node as visited
visited[i] = true;
// Until the queue is empty
while (q.length > 0) {
// Get the node and its parent
let [node, parent] = q.shift();
// Traverse all the neighbors
for (let it of adj[node]) {
// If not visited
if (!visited[it]) {
// Mark the node as visited
visited[it] = true;
/* Push the new node in queue
with curr node as parent */
q.push([it, node]);
}
/* Else if it is visited with some
different parent a cycle is detected */
else if (it !== parent) {
return true;
}
}
}
return false;
}
// Function to detect cycle in an undirected graph.
isCycle(V, adj) {
let visited = new Array(V).fill(false);
let ans = false;
// Start Traversal from every unvisited node
for (let i = 0; i < V; i++) {
if (!visited[i]) {
// Start BFS traversal and update result
ans = this.bfs(i, adj, visited);
// Break if a cycle is detected
if (ans) break;
}
}
return ans;
}
}
const V = 6;
const adj = [
[1, 3],
[0, 2, 4],
[1, 5],
[0, 4],
[1, 3, 5],
[2, 4]
];
// Creating an instance of Solution class
const sol = new Solution();
// Function call to detect cycle in given graph.
const ans = sol.isCycle(V, adj);
// Output
if (ans)
console.log("The given graph contains a cycle.");
else
console.log("The given graph does not contain a cycle.");
Complexity Analysis:
Time Complexity: O(V + E)
(where V is the number of nodes and E is the number of edges in the graph)
Traversing the complete graph overall which taken O(V+E) time.
Space Complexity: O(V)
Visited array takes O(V) space and in the worst case queue will store all nodes taking O(V) space.
Intuition:
In an undirected graph, a cycle is formed when a path exists that returns to the starting vertex without reusing an edge. The key idea is that during traversal (e.g., using Depth-First Search (BFS) for this approach), if we encounter a vertex that has already been visited and is not the immediate parent of the current vertex, a cycle exists.
Approach:
- A helper function performs DFS to detect cycles, keeping track of nodes and their parents. For each unvisited node, initialize the mark the node as visited.
- Traverse the neighbors of the node:
- If a neighbor is unvisited, mark it visited and recursively perform DFS from it.
- If a neighbor is visited and not the parent, a cycle is detected.
- Return true if any cycle is found during traversal.
Dry Run:
Solution:
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to perform DFS traversal
bool dfs(int i, vector<int> adj[],
vector<bool> &visited,
int prev) {
// Mark the node as visited
visited[i] = true;
// Traverse all the neighbors
for(auto node : adj[i]) {
// If not visited
if(!visited[node]) {
/* Recursively perform DFS, and
return true if cycle is found */
if(dfs(node, adj, visited, i)) {
return true;
}
}
/* Else if it is visited with some
different parent a cycle is detected */
else if(node != prev){
return true;
}
}
// Return false if no cycle is detected
return false;
}
public:
// Function to detect cycle in an undirected graph.
bool isCycle(int V, vector<int> adj[]) {
// Visited array
vector<bool> visited(V, false);
// Start Traversal from every unvisited node
for(int i=0; i<V; i++) {
if(!visited[i]) {
/* Start DFS traversal, and
return true if cycle is found */
if(dfs(i, adj, visited, -1)) {
return true;
}
}
}
// Return false if no cycle is detected
return false;
}
};
int main() {
int V = 6;
vector<int> adj[V] = {
{1, 3},
{0, 2, 4},
{1, 5},
{0, 4},
{1, 3, 5},
{2, 4}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to detect
cycle in given graph. */
bool ans = sol.isCycle(V, adj);
// Output
if(ans)
cout << "The given graph contains a cycle.";
else
cout << "The given graph does not contain a cycle.";
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384
import java.util.*;
class Solution {
// Function to perform DFS traversal
private boolean dfs(int i, List<Integer> adj[],
boolean[] visited, int prev) {
// Mark the node as visited
visited[i] = true;
// Traverse all the neighbors
for (int node : adj[i]) {
// If not visited
if (!visited[node]) {
/* Recursively perform DFS, and
return true if cycle is found */
if (dfs(node, adj, visited, i)) {
return true;
}
}
/* Else if it is visited with some
different parent a cycle is detected */
else if (node != prev) {
return true;
}
}
// Return false if no cycle is detected
return false;
}
// Function to detect cycle in an undirected graph.
public boolean isCycle(int V, List<Integer> adj[]) {
// Visited array
boolean[] visited = new boolean[V];
// Start Traversal from every unvisited node
for (int i = 0; i < V; i++) {
if (!visited[i]) {
/* Start DFS traversal, and
return true if cycle is found */
if (dfs(i, adj, visited, -1)) {
return true;
}
}
}
// Return false if no cycle is detected
return false;
}
public static void main(String[] args) {
int V = 6;
List<Integer> adj[] = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
adj[0].addAll(Arrays.asList(1, 3));
adj[1].addAll(Arrays.asList(0, 2, 4));
adj[2].addAll(Arrays.asList(1, 5));
adj[3].addAll(Arrays.asList(0, 4));
adj[4].addAll(Arrays.asList(1, 3, 5));
adj[5].addAll(Arrays.asList(2, 4));
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to detect
cycle in given graph. */
boolean ans = sol.isCycle(V, adj);
// Output
if (ans)
System.out.println("The given graph contains a cycle.");
else
System.out.println("The given graph does not contain a cycle.");
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
class Solution:
# Function to perform DFS traversal
def dfs(self, i, adj, visited, prev):
# Mark the node as visited
visited[i] = True
# Traverse all the neighbors
for node in adj[i]:
# If not visited
if not visited[node]:
# Recursively perform DFS, and
# return true if cycle is found
if self.dfs(node, adj, visited, i):
return True
# Else if it is visited with some
# different parent a cycle is detected
elif node != prev:
return True
# Return false if no cycle is detected
return False
# Function to detect cycle in an undirected graph.
def isCycle(self, V, adj):
# Visited array
visited = [False] * V
# Start Traversal from every unvisited node
for i in range(V):
if not visited[i]:
# Start DFS traversal, and
# return true if cycle is found
if self.dfs(i, adj, visited, -1):
return True
# Return false if no cycle is detected
return False
if __name__ == "__main__":
V = 6
adj = [
[1, 3],
[0, 2, 4],
[1, 5],
[0, 4],
[1, 3, 5],
[2, 4]
]
''' Creating an instance of
Solution class '''
sol = Solution()
''' Function call to detect
cycle in given graph. '''
ans = sol.isCycle(V, adj)
# Output
if ans:
print("The given graph contains a cycle.")
else:
print("The given graph does not contain a cycle.")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
class Solution {
// Function to perform DFS traversal
dfs(i, adj, visited, prev) {
// Mark the node as visited
visited[i] = true;
// Traverse all the neighbors
for (let node of adj[i]) {
// If not visited
if (!visited[node]) {
/* Recursively perform DFS, and
return true if cycle is found */
if (this.dfs(node, adj, visited, i)) {
return true;
}
}
/* Else if it is visited with some
different parent a cycle is detected */
else if (node !== prev) {
return true;
}
}
// Return false if no cycle is detected
return false;
}
// Function to detect cycle in an undirected graph.
isCycle(V, adj) {
// Visited array
let visited = new Array(V).fill(false);
// Start Traversal from every unvisited node
for (let i = 0; i < V; i++) {
if (!visited[i]) {
/* Start DFS traversal, and
return true if cycle is found */
if (this.dfs(i, adj, visited, -1)) {
return true;
}
}
}
// Return false if no cycle is detected
return false;
}
}
const main = () => {
const V = 6;
const adj = [
[1, 3],
[0, 2, 4],
[1, 5],
[0, 4],
[1, 3, 5],
[2, 4]
];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to detect
cycle in given graph. */
const ans = sol.isCycle(V, adj);
// Output
if (ans)
console.log("The given graph contains a cycle.");
else
console.log("The given graph does not contain a cycle.");
};
main();
Complexity Analysis:
Time Complexity: O(V + E)
(where V is the number of nodes and E is the number of edges in the graph)
Traversing the complete graph overall which taken O(V+E) time.
Space Complexity: O(V)
Visited array takes O(V) space and in the worst case recursion stack will store O(V) calls taking O(V) space.
Frequently Occurring Doubts
Q: Why check the parent in DFS for cycles?
A: In an undirected graph, a visited neighbor could be the previous node in traversal, which is not a cycle.
Q: Why use Union-Find for cycle detection?
A: Union-Find tracks connected components efficiently, detecting if two nodes already belong to the same component when an edge is added.
Interview Followup Questions
Q: How can we find all cycles instead of just detecting one?
A: Modify DFS to store path traces and return all cycle paths.
Q: What if the graph was dynamically changing (edges being added/removed)?
A: Use incremental DSU updates to detect cycles in real-time.
Notes
Code
✅ Testcase
Input: {'V': '6', 'Edges': '[[0, 1], [0, 3], [1, 2], [1, 4], [2, 5], [3, 4], [4, 5]]'}
Expected:
True
True
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '4', 'Edges': '[[0, 1], [0, 2], [2, 3]]'}
Expected:
False
False
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '4', 'Edges': '[[0,1],[0,2],[1,2],[2,3]]'}
Expected:
True
True
Actual: -
Time: -
sec
Status: Waiting
Facts
- • Fact: Detecting cycles in a graph is a fundamental problem that has a wide array of applications in the software industry
- • It is used in networking and telecommunication for finding routing loops or cyclical data dependencies
- • Also, it finds usage in DevOps for spotting potential infinite loops in tasks automation like ansible, puppet, etc
- • More so, in social networking applications like Facebook or LinkedIn, it can help track circular friend requests or connections
- • Algorithms for detecting cycles are extensively used in garbage collection mechanism in programming languages like Python, Java and Javascript to identify and clean up objects that are no longer needed by the program to efficiently manage memory