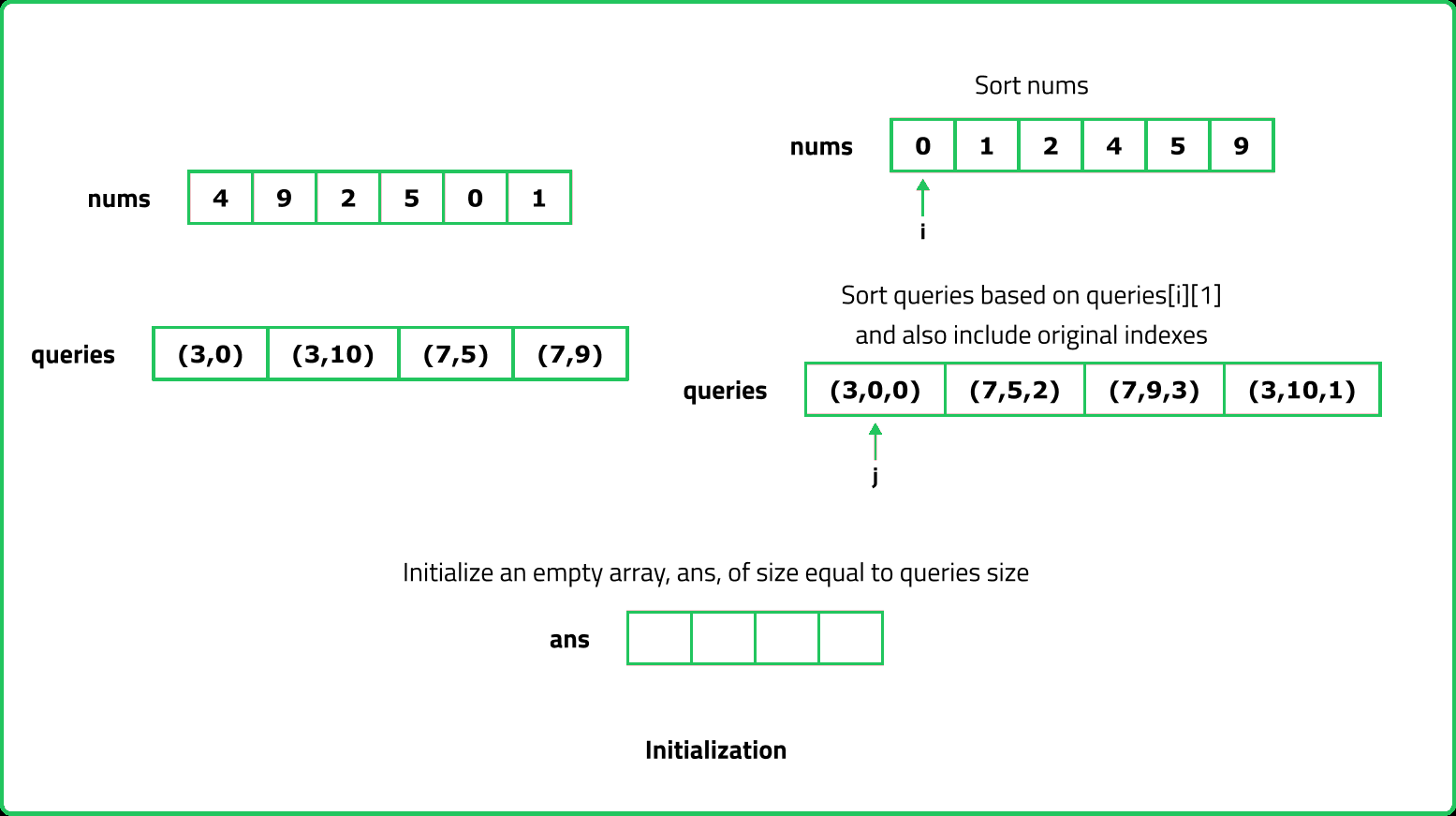
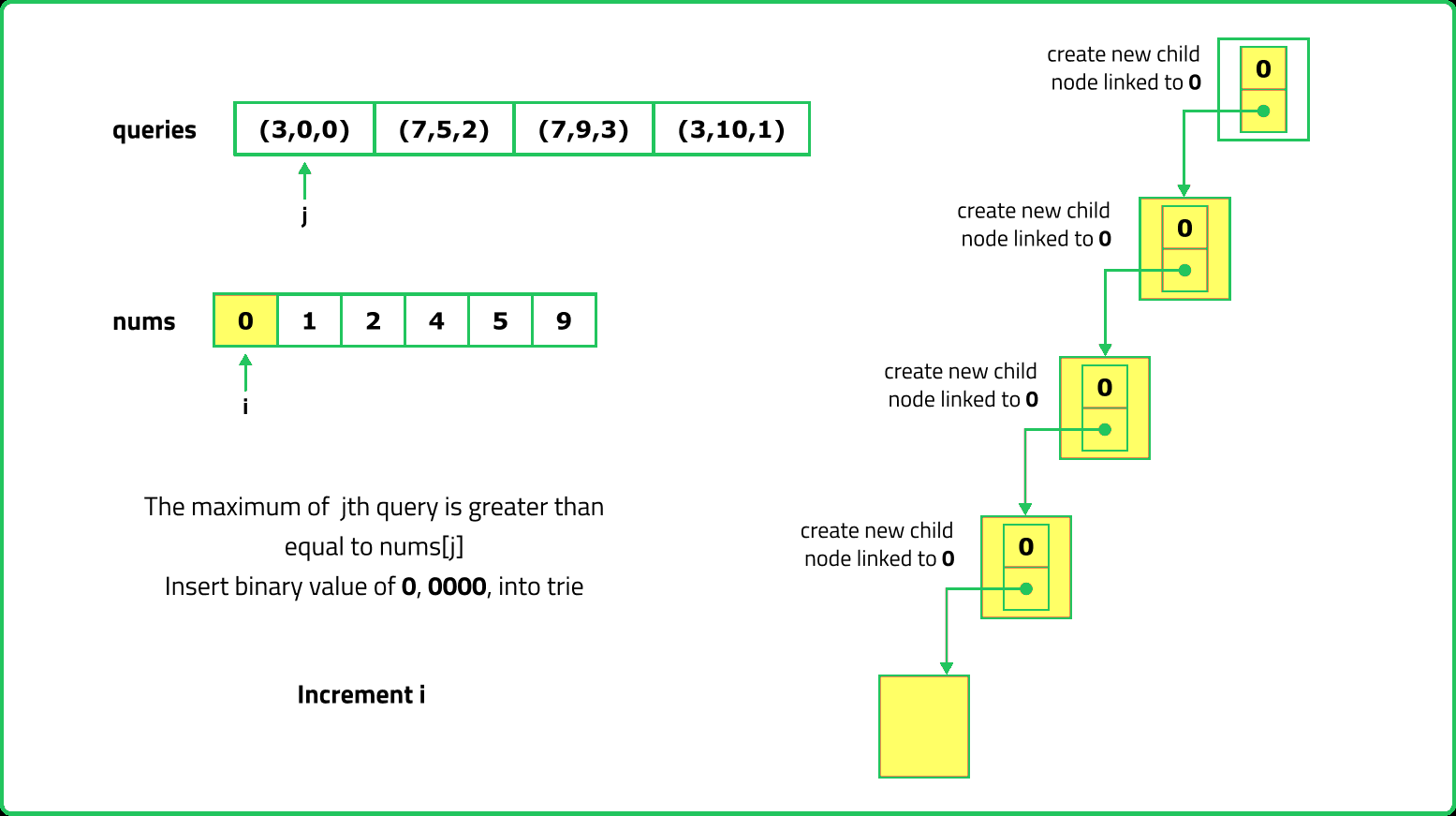
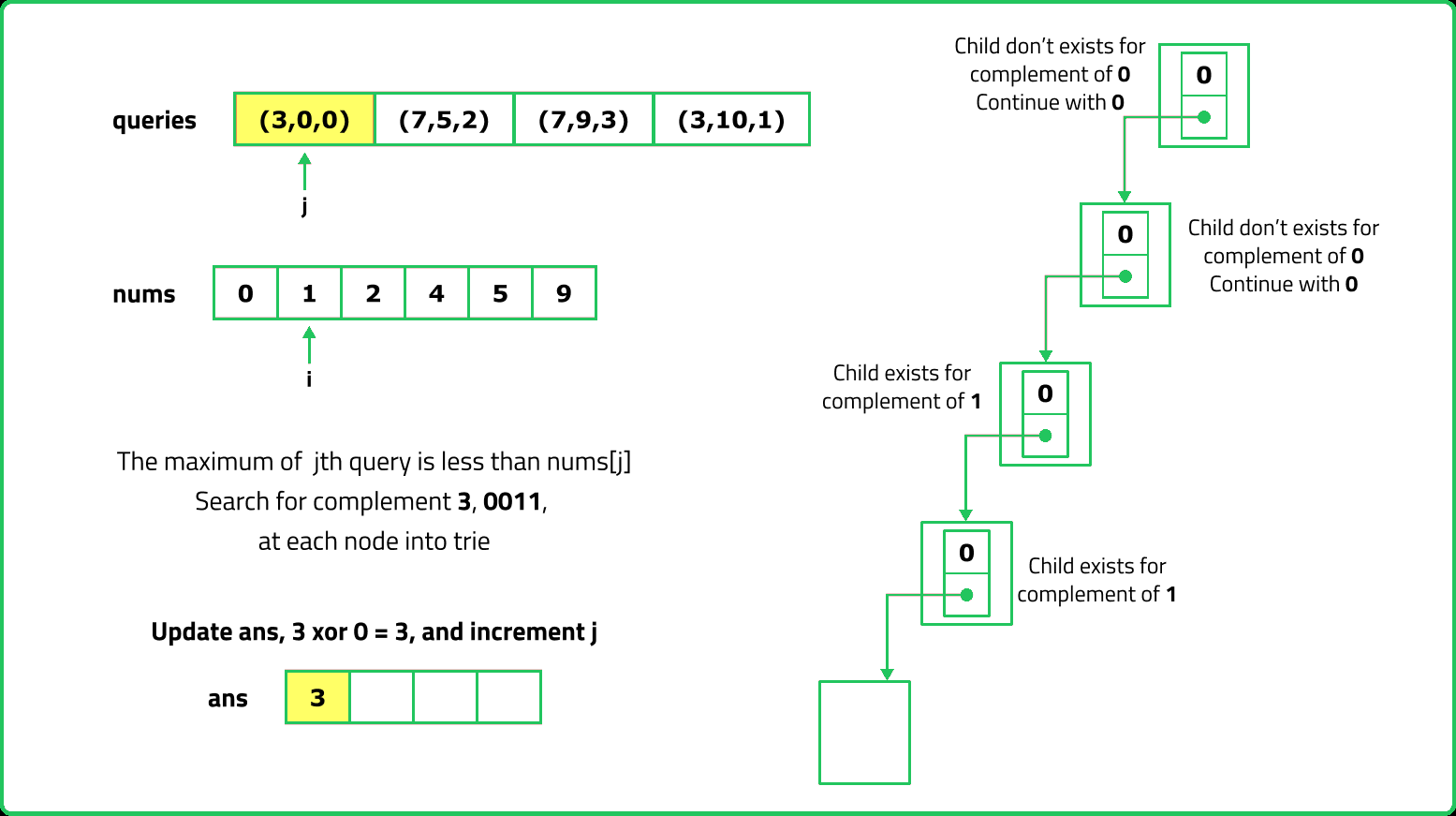
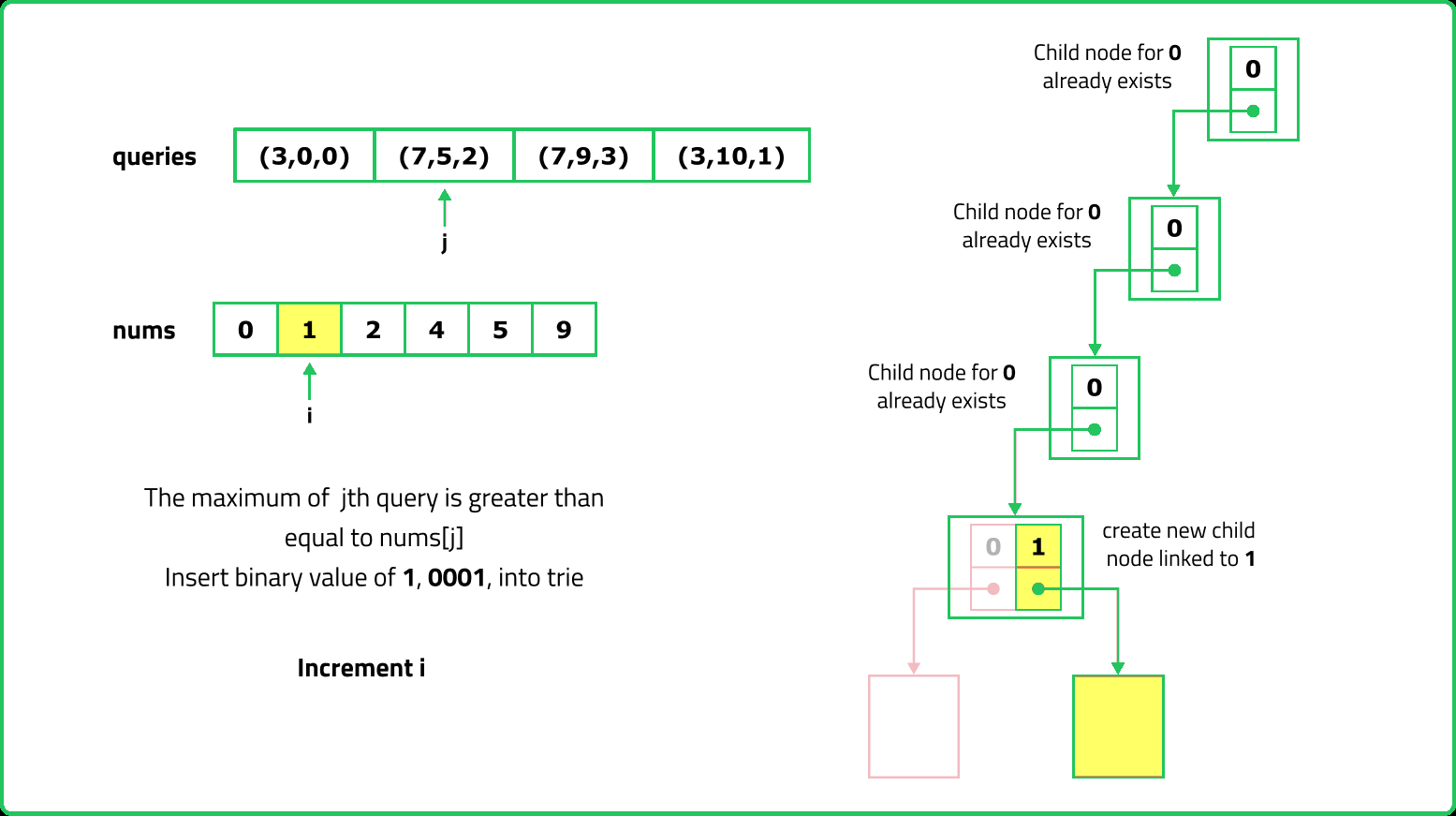
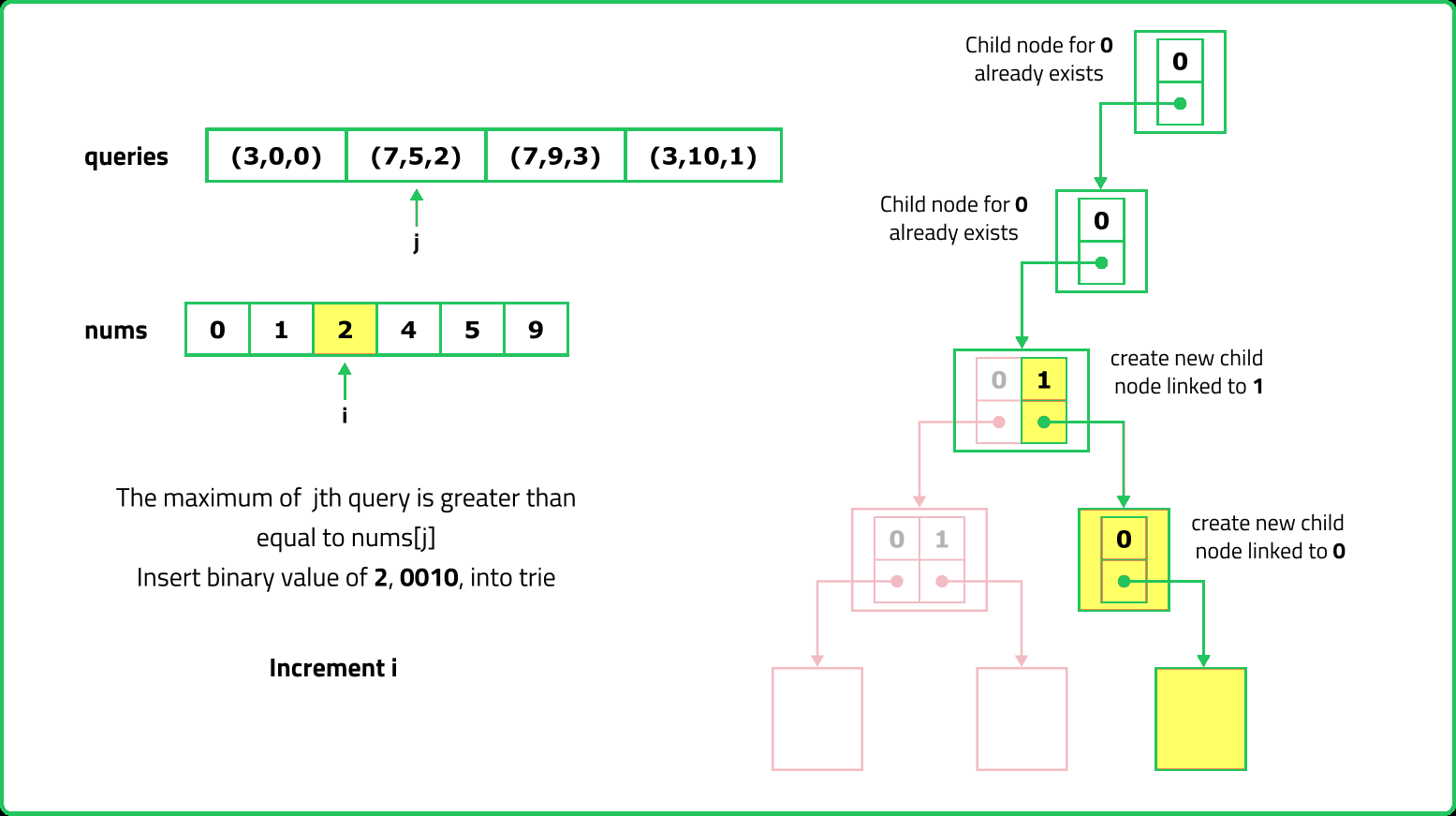
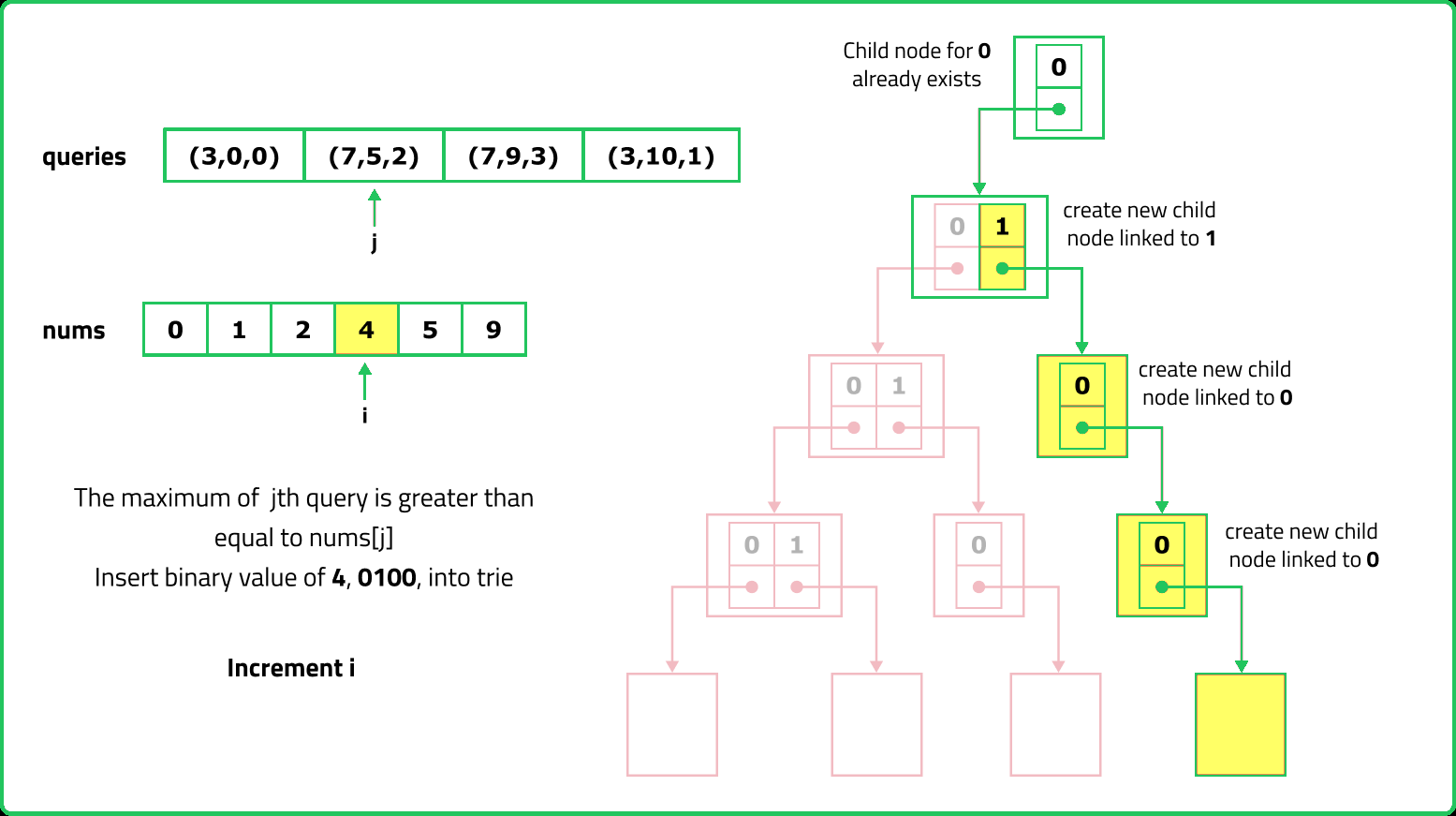
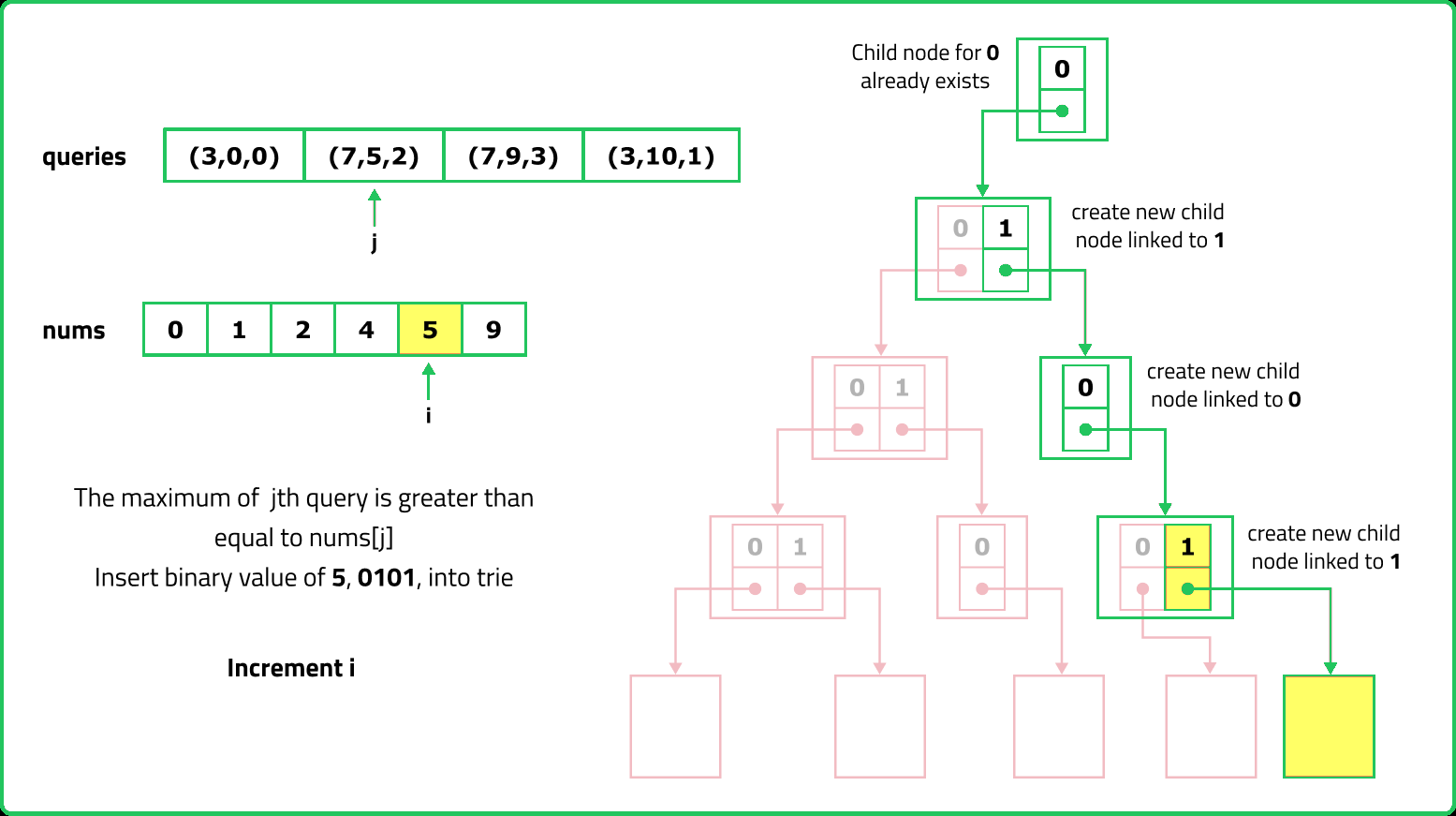
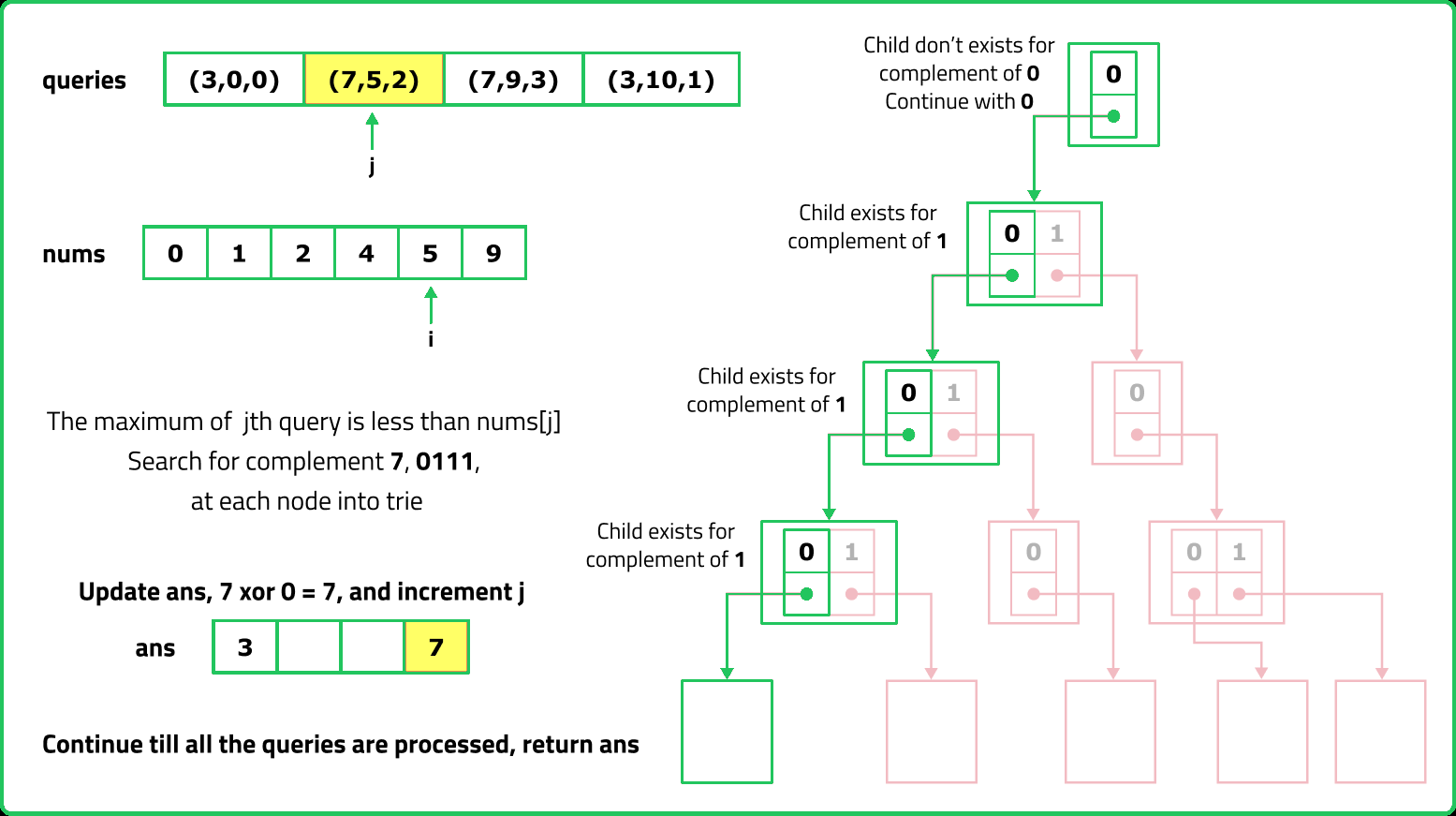
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159
#include <bits/stdc++.h>
using namespace std;
// Node Structure for Trie
struct Node {
Node *links[2];
bool containsKey(int ind) {
return (links[ind] != NULL);
}
Node* get(int ind) {
return links[ind];
}
void put(int ind, Node* node) {
links[ind] = node;
}
};
// Definition for Trie data
class Trie {
private:
Node* root;
public:
// Constructor
Trie() {
root = new Node();
}
// Function to insert
void insert(int num) {
// Start traversal
Node* node = root;
/* Traverse each bit of the number
from the most significant bit to the
least significant bit*/
for (int i = 31; i >= 0; i--) {
int bit = (num >> i) & 1;
/*If the current node doesn't have
a child node at the current bit,
create one*/
if (!node->containsKey(bit)) {
node->put(bit, new Node());
}
/* Move to the child node
corresponding to the
current bit*/
node = node->get(bit);
}
}
// Function to find maximum XOR
int findMax(int num) {
Node* node = root;
int maxNum = 0;
/*Traverse each bit of the number from
the most significant bit to the least
significant bit extract the i-th
bit of the number.
If there exists a different bit
in the trie at the current
position, choose it to maximize XOR*/
for (int i = 31; i >= 0; i--) {
int bit = (num >> i) & 1;
if (node->containsKey(!bit)) {
maxNum = maxNum | (1 << i);
node = node->get(!bit);
} else {
node = node->get(bit);
}
}
// Return maximum XOR value
return maxNum;
}
};
// Solution class to handle queries
class Solution {
public:
// Function to handle the maximize XOR queries
vector<int> maximizeXor(vector<int>& nums, vector<vector<int>>& queries) {
// Initialize vector to store results of queries
vector<int> ans(queries.size(), 0);
// Vector to store offline queries
vector<pair<int, pair<int, int>>> offlineQueries;
// Sort the array of numbers
sort(nums.begin(), nums.end());
// Convert queries to offline queries and store them in a vector
int index = 0;
for (auto &it : queries) {
offlineQueries.push_back({it[1], {it[0], index++}});
}
// Sort queries based on their end points
sort(offlineQueries.begin(), offlineQueries.end());
int i = 0;
int n = nums.size();
Trie trie;
// Process each query
for (auto &it : offlineQueries) {
// Insert numbers
while (i < n && nums[i] <= it.first) {
trie.insert(nums[i]);
i++;
}
/*If there are numbers inserted into the trie,
find the maximum XOR value for the query range*/
if (i != 0)
ans[it.second.second] = trie.findMax(it.second.first);
else
ans[it.second.second] = -1;
}
// Return results
return ans;
}
};
int main() {
// Create instance of Solution class
Solution sol;
// Input array of numbers
vector<int> nums = {0, 1, 2, 3, 4};
// Queries in the form of [x, m]
vector<vector<int>> queries = {{3, 1}, {1, 3}, {5, 6}};
// Get the results of the maximize XOR queries
vector<int> result = sol.maximizeXor(nums, queries);
// Output the results
cout << "Result of Max XOR Queries:" << endl;
for (int i = 0; i < result.size(); ++i) {
cout << "Query " << i+1 << ": " << result[i] << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148
import java.util.*;
// Node Structure for Trie
class Node {
Node[] links = new Node[2];
boolean containsKey(int ind) {
return links[ind] != null;
}
Node get(int ind) {
return links[ind];
}
void put(int ind, Node node) {
links[ind] = node;
}
}
// Definition for Trie data structure
class Trie {
private Node root;
// Constructor
Trie() {
root = new Node();
}
// Function to insert a number into the trie
void insert(int num) {
// Start traversal
Node node = root;
/* Traverse each bit of the number
from the most significant bit to the
least significant bit */
for (int i = 31; i >= 0; i--) {
int bit = (num >> i) & 1;
/* If the current node doesn't have
a child node at the current bit,
create one */
if (!node.containsKey(bit)) {
node.put(bit, new Node());
}
/* Move to the child node
corresponding to the
current bit */
node = node.get(bit);
}
}
// Function to find maximum XOR
int findMax(int num) {
Node node = root;
int maxNum = 0;
/* Traverse each bit of the number from
the most significant bit to the least
significant bit extract the i-th
bit of the number.
If there exists a different bit
in the trie at the current
position, choose it to maximize XOR */
for (int i = 31; i >= 0; i--) {
int bit = (num >> i) & 1;
if (node.containsKey(1 - bit)) {
maxNum = maxNum | (1 << i);
node = node.get(1 - bit);
} else {
node = node.get(bit);
}
}
// Return maximum XOR value
return maxNum;
}
}
// Solution class to handle queries
class Solution {
// Function to handle the maximize XOR queries
public int[] maximizeXor(int[] nums, int[][] queries) {
// Initialize array to store results of queries
int[] ans = new int[queries.length];
// List to store offline queries
List<int[]> offlineQueries = new ArrayList<>();
// Sort the array of numbers
Arrays.sort(nums);
// Convert queries to offline queries and store them in a list
for (int i = 0; i < queries.length; i++) {
offlineQueries.add(new int[]{queries[i][1], queries[i][0], i});
}
// Sort queries based on their end points
offlineQueries.sort(Comparator.comparingInt(a -> a[0]));
int i = 0;
Trie trie = new Trie();
// Process each query
for (int[] query : offlineQueries) {
// Insert numbers
while (i < nums.length && nums[i] <= query[0]) {
trie.insert(nums[i]);
i++;
}
/* If there are numbers inserted into the trie,
find the maximum XOR value for the query range */
if (i != 0)
ans[query[2]] = trie.findMax(query[1]);
else
ans[query[2]] = -1;
}
// Return results
return ans;
}
public static void main(String[] args) {
// Create instance of Solution class
Solution sol = new Solution();
// Input array of numbers
int[] nums = {0, 1, 2, 3, 4};
// Queries in the form of [x, m]
int[][] queries = {{3, 1}, {1, 3}, {5, 6}};
// Get the results of the maximize XOR queries
int[] result = sol.maximizeXor(nums, queries);
// Output the results
System.out.println("Result of Max XOR Queries:");
for (int i = 0; i < result.length; ++i) {
System.out.println("Query " + (i + 1) + ": " + result[i]);
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117
# Node Structure for Trie
class Node:
def __init__(self):
# Initialize child links (0 and 1)
self.links = [None, None]
# Check if a child node exists at a given index (0 or 1)
def contains_key(self, ind):
return self.links[ind] is not None
# Get the child node at a given index (0 or 1)
def get(self, ind):
return self.links[ind]
# Set the child node at a given index (0 or 1)
def put(self, ind, node):
self.links[ind] = node
# Definition for Trie data structure
class Trie:
def __init__(self):
# Initialize root node
self.root = Node()
# Function to insert a number into the trie
def insert(self, num):
# Start traversal
node = self.root
# Traverse each bit of the number
for i in range(31, -1, -1):
bit = (num >> i) & 1
# If the current node doesn't have a child node at the current bit, create one
if not node.contains_key(bit):
node.put(bit, Node())
# Move to the child node corresponding to the current bit
node = node.get(bit)
# Function to find the maximum XOR value achievable with a given number
def find_max(self, num):
node = self.root
max_num = 0
# Traverse each bit of the number
for i in range(31, -1, -1):
bit = (num >> i) & 1
# If there exists a different bit in the trie at the current position, choose it to maximize XOR
if node.contains_key(1 - bit):
max_num = max_num | (1 << i)
node = node.get(1 - bit)
else:
node = node.get(bit)
# Return the maximum XOR value
return max_num
# Solution class to handle queries
class Solution:
# Function to handle the maximize XOR queries
def maximizeXor(self, nums, queries):
# Initialize list to store results of queries
ans = [0] * len(queries)
# List to store offline queries
offline_queries = []
# Sort the array of numbers
nums.sort()
# Convert queries to offline queries and store them in a list
for index, query in enumerate(queries):
offline_queries.append((query[1], query[0], index))
# Sort queries based on their end points
offline_queries.sort()
i = 0
trie = Trie()
# Process each query
for m, x, query_index in offline_queries:
# Insert numbers into the trie until the current query's end point
while i < len(nums) and nums[i] <= m:
trie.insert(nums[i])
i += 1
# If there are numbers inserted into the trie, find the maximum XOR value for the query range
if i != 0:
ans[query_index] = trie.find_max(x)
else:
ans[query_index] = -1
# Return results
return ans
# Main function to test the Solution class
if __name__ == "__main__":
# Create instance of Solution class
sol = Solution()
# Input array of numbers
nums = [0, 1, 2, 3, 4]
# Queries in the form of [x, m]
queries = [[3, 1], [1, 3], [5, 6]]
# Get the results of the maximize XOR queries
result = sol.maximizeXor(nums, queries)
# Output the results
print("Result of Max XOR Queries:")
for i in range(len(result)):
print(f"Query {i + 1}: {result[i]}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149
// Node Structure for Trie
class Node {
constructor() {
this.links = [null, null];
}
containsKey(ind) {
return this.links[ind] !== null;
}
get(ind) {
return this.links[ind];
}
put(ind, node) {
this.links[ind] = node;
}
}
// Definition for Trie data structure
class Trie {
constructor() {
// Initialize root node
this.root = new Node();
}
// Function to insert a number into the trie
insert(num) {
// Start traversal
let node = this.root;
/* Traverse each bit of the number
from the most significant bit to the
least significant bit */
for (let i = 31; i >= 0; i--) {
const bit = (num >> i) & 1;
/* If the current node doesn't have
a child node at the current bit,
create one */
if (!node.containsKey(bit)) {
node.put(bit, new Node());
}
/* Move to the child node
corresponding to the
current bit */
node = node.get(bit);
}
}
// Function to find maximum XOR
findMax(num) {
let node = this.root;
let maxNum = 0;
/* Traverse each bit of the number from
the most significant bit to the least
significant bit extract the i-th
bit of the number.
If there exists a different bit
in the trie at the current
position, choose it to maximize XOR */
for (let i = 31; i >= 0; i--) {
const bit = (num >> i) & 1;
if (node.containsKey(1 - bit)) {
maxNum = maxNum | (1 << i);
node = node.get(1 - bit);
} else {
node = node.get(bit);
}
}
// Return maximum XOR value
return maxNum;
}
}
// Solution class to handle queries
class Solution {
// Function to handle the maximize XOR queries
maximizeXor(nums, queries) {
// Initialize array to store results of queries
const ans = new Array(queries.length).fill(0);
// Array to store offline queries
const offlineQueries = [];
// Sort the array of numbers
nums.sort((a, b) => a - b);
// Convert queries to offline queries and store them in an array
queries.forEach((query, index) => {
offlineQueries.push([query[1], query[0], index]);
});
// Sort queries based on their end points
offlineQueries.sort((a, b) => a[0] - b[0]);
let i = 0;
const trie = new Trie();
// Process each query
offlineQueries.forEach(query => {
// Insert numbers
while (i < nums.length && nums[i] <= query[0]) {
trie.insert(nums[i]);
i++;
}
/* If there are numbers inserted into the trie,
find the maximum XOR value for the query range */
if (i !== 0) {
ans[query[2]] = trie.findMax(query[1]);
} else {
ans[query[2]] = -1;
}
});
// Return results
return ans;
}
}
// Main function to test the Solution class
const main = () => {
// Create instance of Solution class
const sol = new Solution();
// Input array of numbers
const nums = [0, 1, 2, 3, 4];
// Queries in the form of [x, m]
const queries = [[3, 1], [1, 3], [5, 6]];
// Get the results of the maximize XOR queries
const result = sol.maximizeXor(nums, queries);
// Output the results
console.log("Result of Max XOR Queries:");
result.forEach((res, i) => {
console.log(`Query ${i + 1}: ${res}`);
});
};
// Call the main function
main();