Split array - largest sum

Binary Search FAQs Hard Go Ad-Free - ₹20/mo

Given an integer array a of size n and an integer k. Split the array a into k non-empty subarrays such that the largest sum of any subarray is minimized. Return the minimized largest sum of the split.

Examples:

Input: a = [1, 2, 3, 4, 5], k = 3

Output:6

Explanation: There are many ways to split the array a[] into k consecutive subarrays. The best way to do this is to split the array a[] into [1, 2, 3], [4], and [5], where the largest sum among the three subarrays is only 6.

Input: a = [3,5,1], k = 3

Output: 5

Explanation: There is only one way to split the array a[] into 3 subarrays, i.e., [3], [5], and [1]. The largest sum among these subarrays is 5.

Input: a = [1, 2, 3, 4, 5], k = 2

Constraints

1 ≤ n ≤ 10⁴
1 ≤ k ≤ n
1 ≤ a[i] ≤ 10⁴

Hints

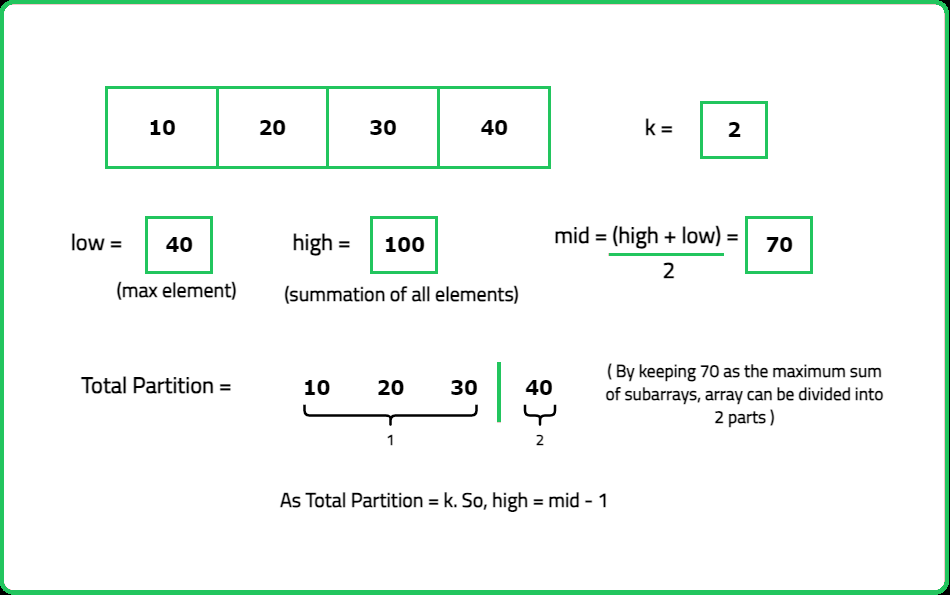
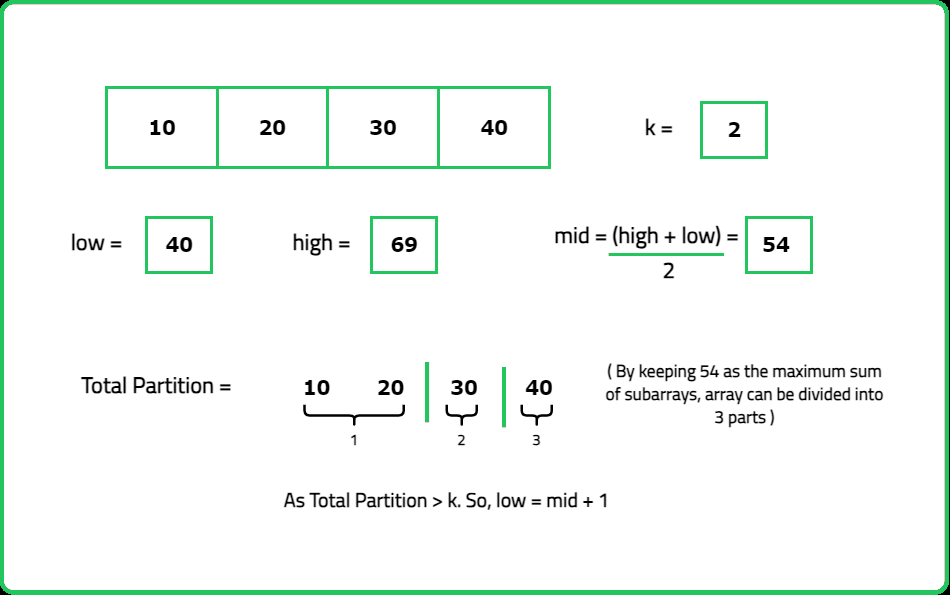
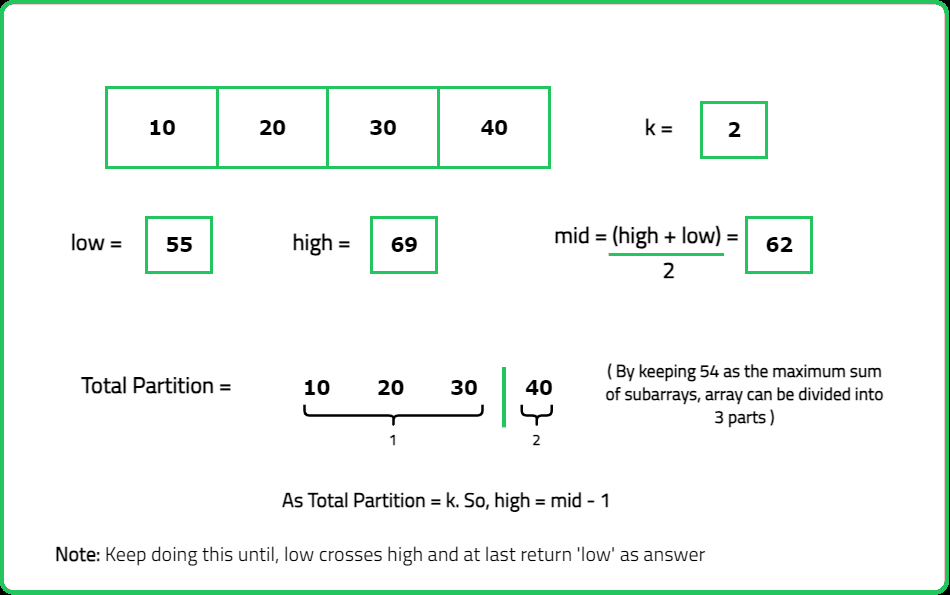
Use binary search to find the smallest possible value of the maximum subarray sum.
"If mid is feasible (subarrays can be formed with a maximum sum ≤mid), search for a smaller maximum sum (high=mid). If mid is not feasible, search for a larger maximum sum (low=mid+1)."

Company Tags

Siemens Healthineers Splunk Airbnb Optum Ernst & Young Robinhood Reddit Seagate Technology Roche Rockstar Games Alibaba AMD Walmart MongoDB Rakuten Qualcomm GE Healthcare Etsy Deloitte Electronic Arts IBM Epic Games Broadcom NVIDIA Freshworks Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition:

The idea is to utilize the Binary Search algorithm to find the optimal solution for this problem. The search range for the problem is [max, sum], where max represents the maximum element of the array, and sum denotes the total sum of all elements in the array. This range is inherently sorted, allowing binary search to efficiently determine the appropriate half to explore in each iteration, thereby reducing the search space by half.

In this specific problem, the condition for eliminating one half of the search space is based on whether the number of partitions exceeds the given limit. If it does, it indicates that the current value of 'mid' is too small, so the left half is eliminated. Otherwise, the current 'mid' value is a potential answer, which is stored, and the search continues in the right half.

Approach:

Working of largestSubarraySumMinimized(arr,k):

Initialize two pointers low and high: Initially, low will point to maximum element of the array and high will point to the sum of all the elements of the array.
Intialize a while loop which will run till low is less than or equal to high. Calculate mid using the following formula: mid = (low+high) // 2 ( ‘//’ refers to integer division).
Use the countPartition() function to count the the number of partitions that can be made based on the potential value of ‘maxSum’, represented by the variable 'mid'.
If partitions is greater than k, it can be concluded that the number ‘mid’ is smaller than our answer. So, eliminate the left half and consider the right half(i.e. low = mid+1). Otherwise, the value mid is one of the possible answers. But the minimum value is needed, so, eliminate the right half and consider the left half(i.e. high = mid-1).
Finally, when the loop terminates, return the value of low as the pointer will be pointing to the answer.

Working of countPartitions(arr, maxSum):

Start with n = a.size(), which gives the number of elements in the vector a. Initialize partitions to 1, assuming at least one partition is required to cover all elements and also initialize subarraySum to 0, which will keep track of the sum of elements in the current subarray being considered.
Iterate in the array and check if adding the current element to subarraySum will keep the sum within the maxSum limit. If true, add it to the current. If adding current element would exceed maxSum, it indicates that current element should start a new subarray (partition). Increment the partitions counter to start a new partition. Reset subarraySum to a[i] to begin the new subarray with the current element.
After iterating through all elements in the array, return partitions, which represents the count of partitions needed.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to count partitions such 
    that each partition has sum <= maxSum*/
    int countPartitions(vector<int> &a, int maxSum) {
        int n = a.size();
        int partitions = 1;
        long long subarraySum = 0;

        for (int i = 0; i < n; i++) {
            if (subarraySum + a[i] <= maxSum) {
                // Add element to the current subarray
                subarraySum += a[i];
            } else {
                // Start a new subarray with current element
                partitions++;
                subarraySum = a[i];
            }
        }

        return partitions;
    }

public:
    /* Function to find the largest minimum
    subarray sum with at most k partitions*/
    int largestSubarraySumMinimized(vector<int> &a, int k) {
        
        // Initialize binary search boundaries
        int low = *max_element(a.begin(), a.end()); 
        int high = accumulate(a.begin(), a.end(), 0);

        // Apply binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            int partitions = countPartitions(a, mid);

            if (partitions > k) {
                /*If partitions exceed k, increase 
                the minimum possible subarray sum*/
                low = mid + 1;
            } 
            else {
                /*If partitions are within k, try to
                minimize the subarray sum further*/
                high = mid - 1;
            }
        }

        /* After binary search, 'low' will 
        be the largest minimum subarray sum
        with at most k partitions*/
        return low;
    }
};

int main() {
    vector<int> a = {10, 20, 30, 40};
    int k = 2;

    // Create an instance of the Solution class
    Solution sol;

    int ans = sol.largestSubarraySumMinimized(a, k);
    cout << "The answer is: " << ans << "\n";
    return 0;
}
import java.util.*;

class Solution {
    /* Function to count partitions such 
    that each partition has sum <= maxSum*/
    private int countPartitions(int[] a, int maxSum) {
        int n = a.length;
        int partitions = 1;
        long subarraySum = 0;

        for (int i = 0; i < n; i++) {
            if (subarraySum + a[i] <= maxSum) {
                // Add element to the current subarray
                subarraySum += a[i];
            } else {
                // Start a new subarray with current element
                partitions++;
                subarraySum = a[i];
            }
        }

        return partitions;
    }

    /* Function to find the largest minimum
    subarray sum with at most k partitions*/
    public int largestSubarraySumMinimized(int[] a, int k) {
        
        // Initialize binary search boundaries
        int low = a[0];
        int high = 0;
        
        //Find maximum and summation
        for (int i = 0; i < a.length; i++) {
            low = Math.max(low, a[i]);
            high += a[i];
        }
        // Apply binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            int partitions = countPartitions(a, mid);

            if (partitions > k) {
                /* If partitions exceed k, increase
                the minimum possible subarray sum*/
                low = mid + 1;
            } 
            else {
                /* If partitions are within k, try to
                minimize the subarray sum further*/
                high = mid - 1;
            }
        }

        /* After binary search, 'low' will 
        be the largest minimum subarray sum
        with at most k partitions*/
        return low;
    }

    public static void main(String[] args) {
        int[] a = {10, 20, 30, 40};
        int k = 2;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        int ans = sol.largestSubarraySumMinimized(a, k);

        // Print the answer
        System.out.println("The answer is: " + ans);
    }
}
class Solution:
    """ Function to count partitions such 
    that each partition has sum <= maxSum"""
    def countPartitions(self, a, maxSum):
        n = len(a)
        partitions = 1
        subarraySum = 0

        for i in range(n):
            if subarraySum + a[i] <= maxSum:
                # Add element to the current subarray
                subarraySum += a[i]
            else:
                # Start a new subarray with current element
                partitions += 1
                subarraySum = a[i]

        return partitions

    """ Function to find the largest minimum 
    subarray sum with at most k partitions"""
    def largestSubarraySumMinimized(self, a, k):
        # Initialize binary search boundaries
        low = max(a)  
        high = sum(a) 

        # Apply binary search
        while low <= high:
            mid = (low + high) // 2
            partitions = self.countPartitions(a, mid)

            if partitions > k:
                """ If partitions exceed k, increase 
                the minimum possible subarray sum"""
                low = mid + 1
            else:
                """ If partitions are within k, try to 
                minimize the subarray sum further"""
                high = mid - 1

        """ After binary search, 'low' will be
        the largest minimum subarray sum with
        at most k partitions"""
        return low

if __name__ == "__main__":
    a = [10, 20, 30, 40]
    k = 2
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Print the answer
    print("The answer is:", sol.largestSubarraySumMinimized(a, k))
class Solution {
    /* Function to count partitions such 
    that each partition has sum <= maxSum*/
    countPartitions(a, maxSum) {
        let n = a.length;
        let partitions = 1;
        let subarraySum = 0;

        for (let i = 0; i < n; i++) {
            if (subarraySum + a[i] <= maxSum) {
                // Add element to the current subarray
                subarraySum += a[i];
            } else {
                // Start a new subarray with current element
                partitions++;
                subarraySum = a[i];
            }
        }

        return partitions;
    }

    /* Function to find the largest minimum 
    subarray sum with at most k partitions*/
    largestSubarraySumMinimized(a, k) {
        
        // Initialize binary search boundaries
        let low = Math.max(...a); 
        let high = a.reduce((acc, curr) => acc + curr, 0); 

        // Apply binary search
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
            let partitions = this.countPartitions(a, mid);

            if (partitions > k) {
                /* If partitions exceed k, increase 
                the minimum possible subarray sum*/
                low = mid + 1;
            } else {
                /* If partitions are within k, try to 
                minimize the subarray sum further*/
                high = mid - 1;
            }
        }

        /* After binary search, 'low' will be
        the largest minimum subarray sum with
        at most k partitions*/
        return low;
    }
}

const a = [10, 20, 30, 40];
const k = 2;

//Create an instance of Solution class
const sol = new Solution();

// Print the answer
console.log("The answer is:", sol.largestSubarraySumMinimized(a, k));

Complexity Analysis:

Time Complexity: O(N * (log(sum - max) + 1)), where N is the size of the array, 'sum' is the sum of all array elements, and 'max' is the maximum element in the array. This complexity arises because binary search is applied within the range [max, sum], and the countPartitions() function is invoked for each value of 'mid'. Inside the countPartitions() function, a loop iterates N times for each call.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Frequently Occurring Doubts

Q: Why use binary search to minimize the largest sum?

A: Testing all possible splits is computationally expensive (O(2^n)). Binary search narrows the range of possible sums, reducing the complexity to O(n⋅log(sum(a)−max(a))).

Q: How is the feasibility of mid checked?

A: Traverse the array and form subarrays: Add elements to the current subarray until adding another element would exceed mid. Start a new subarray and increment the subarray count. If the subarray count exceeds k, mid is not feasible.

Interview Followup Questions

Q: Can this approach handle dynamic updates to the array?

A: For dynamic scenarios, maintain a prefix sum array to quickly recompute sums. Apply the binary search logic on the updated prefix sum.

Q: How would you handle additional constraints, like maximum subarray length?

A: Modify the feasibility check to account for the maximum allowed subarray length. Ensure that the number of elements in each subarray does not exceed the constraint during the traversal.

Notes

Your notes are automatically saved in your browser's local storage and will persist across sessions on this device.

Problem Categories