Longest Consecutive Sequence in an Array

Intuition

One simple approach is to look for sequences of consecutive numbers by utilising linear search in the array. For each number 𝑥 in the array, we'll check if the next numbers like 𝑥+1, 𝑥+2, 𝑥+3, and so on, are also in the array. This is like checking if we can build a chain of numbers that follow each other directly. By doing this for every number in the array, we can find the longest chain of consecutive numbers. Finally, we'll find the length of the longest chain among all the numbers in the array.

Approach

As you iterate through each number in the array, begin by checking if consecutive numbers like ( x+1, x+2, x+3 ), and so on, exist in the array. The occurrence of the next consecutive number can be checked by using linear search.
When you find consecutive numbers, start counting them using a counter. Increment this counter each time you find the next consecutive number in the sequence.
This counter effectively keeps track of how long the current consecutive sequence is as you move through the array and find more consecutive numbers.

Dry Run:-Please refer to the video for the dry-run.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Helper function to perform linear search
    bool linearSearch(vector<int>& a, int num) {
        int n = a.size(); 
        // Traverse through the array 
        for (int i = 0; i < n; i++) {
            if (a[i] == num)
                return true;
        }
        return false;
    }

public:
    // Function to find the longest consecutive sequence
    int longestConsecutive(vector<int>& nums) {
        // If the array is empty
        if (nums.size() == 0) {
            return 0;
        }
        int n = nums.size();
        // Initialize the longest sequence length
        int longest = 1; 

        // Iterate through each element in the array
        for (int i = 0; i < n; i++) {
            // Current element
            int x = nums[i]; 
            // Count of the current sequence
            int cnt = 1; 

            // Search for consecutive numbers
            while (linearSearch(nums, x + 1) == true) {
                // Move to the next number in the sequence
                x += 1; 
                // Increment the count of the sequence
                cnt += 1; 
            }

            // Update the longest sequence length found so far
            longest = max(longest, cnt);
        }
        return longest;
    }
};

int main() {
    vector<int> a = {100, 4, 200, 1, 3, 2};

    // Create an instance of the Solution class
    Solution solution;

    // Function call for longest consecutive sequence
    int ans = solution.longestConsecutive(a);
    cout << "The longest consecutive sequence is " << ans << "\n"; 
    return 0;
}

import java.util.*;

class Solution {
    // Helper function to perform linear search
    private boolean linearSearch(int[] a, int num) {
        int n = a.length;
        // Traverse through the array
        for (int i = 0; i < n; i++) {
            if (a[i] == num)
                return true;
        }
        return false;
    }

    public int longestConsecutive(int[] nums) {
        // If the array is empty
        if (nums.length == 0) {
            return 0;
        }
        int n = nums.length;
        // Initialize the longest sequence length
        int longest = 1;

        // Iterate through each element in the array
        for (int i = 0; i < n; i++) {
            // Current element
            int x = nums[i];
            // Count of the current sequence
            int cnt = 1;

            // Search for consecutive numbers
            while (linearSearch(nums, x + 1) == true) {
                // Move to the next number in the sequence
                x += 1;
                // Increment the count of the sequence
                cnt += 1;
            }

            // Update the longest sequence length found so far
            longest = Math.max(longest, cnt);
        }
        return longest;
    }

    public static void main(String[] args) {
        int[] a = {100, 4, 200, 1, 3, 2};

        // Create an instance of the Solution class
        Solution solution = new Solution();

        // Function call for longest consecutive sequence
        int ans = solution.longestConsecutive(a);
        System.out.println("The longest consecutive sequence is " + ans);
    }
}

class Solution:
    # Helper function to perform linear search
    def linearSearch(self, nums, num):
        n = len(nums)
        # Traverse through the array
        for i in range(n):
            if nums[i] == num:
                return True
        return False

    def longestConsecutive(self, nums):
        # If the array is empty
        if len(nums) == 0:
            return 0
        n = len(nums)
        # Initialize the longest sequence length
        longest = 1

        # Iterate through each element in the array
        for i in range(n):
            # Current element
            x = nums[i]
            # Count of the current sequence
            cnt = 1

            # Search for consecutive numbers
            while self.linearSearch(nums, x + 1):
                # Move to the next number in the sequence
                x += 1
                # Increment the count of the sequence
                cnt += 1

            # Update the longest sequence length found so far
            longest = max(longest, cnt)
        return longest

if __name__ == "__main__":
    a = [100, 4, 200, 1, 3, 2]

    # Create an instance of the Solution class
    solution = Solution()

    # Function call for longest consecutive sequence
    ans = solution.longestConsecutive(a)
    print("The longest consecutive sequence is", ans)

class Solution {
    // Helper function to perform linear search
    linearSearch(nums, num) {
        const n = nums.length;
        // Traverse through the array
        for (let i = 0; i < n; i++) {
            if (nums[i] === num)
                return true;
        }
        return false;
    }

    longestConsecutive(nums) {
        // If the array is empty
        if (nums.length === 0) {
            return 0;
        }
        const n = nums.length;
        // Initialize the longest sequence length
        let longest = 1;

        // Iterate through each element in the array
        for (let i = 0; i < n; i++) {
            // Current element
            let x = nums[i];
            // Count of the current sequence
            let cnt = 1;

            // Search for consecutive numbers
            while (this.linearSearch(nums, x + 1)) {
                // Move to the next number in the sequence
                x += 1;
                // Increment the count of the sequence
                cnt += 1;
            }

            // Update the longest sequence length found so far
            longest = Math.max(longest, cnt);
        }
        return longest;
    }
}

const a = [100, 4, 200, 1, 3, 2];

// Create an instance of the Solution class
const solution = new Solution();

// Function call for longest consecutive sequence
const ans = solution.longestConsecutive(a);
console.log("The longest consecutive sequence is", ans);

Complexity Analysis

Time Complexity: O(N²), here N is the size of the given array. Since we are using nested loops each running for approximately N times. The outer loop traverses for finding the consecutive sequence of every element and the inner loop works for checking if the next value exists in the array or not. Space Complexity: O(1), as we are not using any extra space to solve this problem.

Intuition

A more efficient method involves sorting the array first and then finding the longest consecutive sequence using a simple iteration.

Approach

Begin by sorting the entire array in ascending order. This step helps group consecutive numbers together, simplifying the sequence detection process.
Use a loop to iterate through each element of the sorted array.
Track consecutive sequences by comparing each element arr[i] with the lastSmaller variable. If arr[i] - 1 == lastSmaller, increment the length of the current sequence (cnt) and update lastSmaller to arr[i]. Skip the current element if arr[i] equals lastSmaller, as it's already part of a sequence. If arr[i] is greater than lastSmaller + 1, start a new sequence from arr[i] by updating lastSmaller to arr[i] and reset cnt to 1.
Throughout the iteration, compare cnt with longest and update longest to store the maximum sequence length encountered.

Note: Here, we are distorting the given array by sorting it.

Dry Run:-Please refer to the video for the dry-run.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int n = nums.size();

        // Return 0 if array is empty
        if (n == 0) return 0; 

        sort(nums.begin(), nums.end()); 

        // Track last smaller element
        int lastSmaller = INT_MIN; 
        // Count current sequence length
        int cnt = 0; 
        // Track longest sequence length
        int longest = 1; 

        for (int i = 0; i < n; i++) {
            // If consecutive number exists
            if (nums[i] - 1 == lastSmaller) {
                // Increment sequence count
                cnt += 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            } 
            // If consecutive number doesn't exits
            else if (nums[i] != lastSmaller) {
                // Reset count for new sequence
                cnt = 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            }
            // Update longest if needed
            longest = max(longest, cnt); 
        }
        return longest;
    }
};

int main() {
    vector<int> a = {100, 4, 200, 1, 3, 2}; 

    // Create an instance of solution class
    Solution solution; 
    // Function call for finding longest consecutive sequence
    int ans = solution.longestConsecutive(a); 
    cout << "The longest consecutive sequence is " << ans << "\n";
    return 0;
}

import java.util.*;

class Solution {
    public int longestConsecutive(int[] nums) {
        int n = nums.length;

        // Return 0 if array is empty
        if (n == 0) return 0; 

        Arrays.sort(nums); // Sort the array

        // Track last smaller element
        int lastSmaller = Integer.MIN_VALUE; 
        // Count current sequence length
        int cnt = 0; 
        // Track longest sequence length
        int longest = 1; 

        for (int i = 0; i < n; i++) {
            // If consecutive number exists
            if (nums[i] - 1 == lastSmaller) {
                // Increment sequence count
                cnt += 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            } 
            // If consecutive number doesn't exist
            else if (nums[i] != lastSmaller) {
                // Reset count for new sequence
                cnt = 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            }
            // Update longest if needed
            longest = Math.max(longest, cnt); 
        }
        return longest;
    }

    public static void main(String[] args) {
        int[] a = {100, 4, 200, 1, 3, 2}; 

        // Create an instance of solution class
        Solution solution = new Solution(); 
        // Function call for finding longest consecutive sequence
        int ans = solution.longestConsecutive(a); 
        System.out.println("The longest consecutive sequence is " + ans);
    }
}

class Solution:
    def longestConsecutive(self, nums):
        n = len(nums)

        # Return 0 if array is empty
        if n == 0:
            return 0 

        nums.sort()

        # Track last smaller element
        lastSmaller = float('-inf') 
        # Count current sequence length
        cnt = 0 
        # Track longest sequence length
        longest = 1 

        for i in range(n):
            # If consecutive number exists
            if nums[i] - 1 == lastSmaller:
                # Increment sequence count
                cnt += 1 
                # Update last smaller element
                lastSmaller = nums[i] 
            # If consecutive number doesn't exist
            elif nums[i] != lastSmaller:
                # Reset count for new sequence
                cnt = 1 
                # Update last smaller element
                lastSmaller = nums[i] 
            # Update longest if needed
            longest = max(longest, cnt) 
        return longest

# Sample array
a = [100, 4, 200, 1, 3, 2]

# Create an instance of solution class
solution = Solution() 
# Function call for finding longest consecutive sequence
ans = solution.longestConsecutive(a) 
print("The longest consecutive sequence is", ans)

class Solution {
    longestConsecutive(nums) {
        let n = nums.length;

        // Return 0 if array is empty
        if (n === 0) return 0; 

        nums.sort((a, b) => a - b);

        // Track last smaller element
        let lastSmaller = -Infinity; 
        // Count current sequence length
        let cnt = 0; 
        // Track longest sequence length
        let longest = 1; 

        for (let i = 0; i < n; i++) {
            // If consecutive number exists
            if (nums[i] - 1 === lastSmaller) {
                // Increment sequence count
                cnt += 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            } 
            // If consecutive number doesn't exist
            else if (nums[i] !== lastSmaller) {
                // Reset count for new sequence
                cnt = 1; 
                // Update last smaller element
                lastSmaller = nums[i]; 
            }
            // Update longest if needed
            longest = Math.max(longest, cnt); 
        }
        return longest;
    }
}

// Sample array
const a = [100, 4, 200, 1, 3, 2];

// Create an instance of solution class
const solution = new Solution(); 
// Function call for finding longest consecutive sequence
const ans = solution.longestConsecutive(a); 
console.log("The longest consecutive sequence is " + ans);

Complexity Analysis

Time Complexity: O(NlogN) + O(N), here N is the size of the given array. Here, O(NlogN) is for sorting the array. To find the longest sequence, we use a loop that results in O(N).

Space Complexity: O(1), as we are not using any extra space to solve this problem.

Intuition

In this approach, we refine the brute-force method by focusing only on potential starting numbers of sequences, rather than searching for sequences for every array element. This targeted strategy enhances efficiency using a Set data structure.

Approach

We will use two variables, cnt to store the length of the current sequence and longest to store the maximum length found.

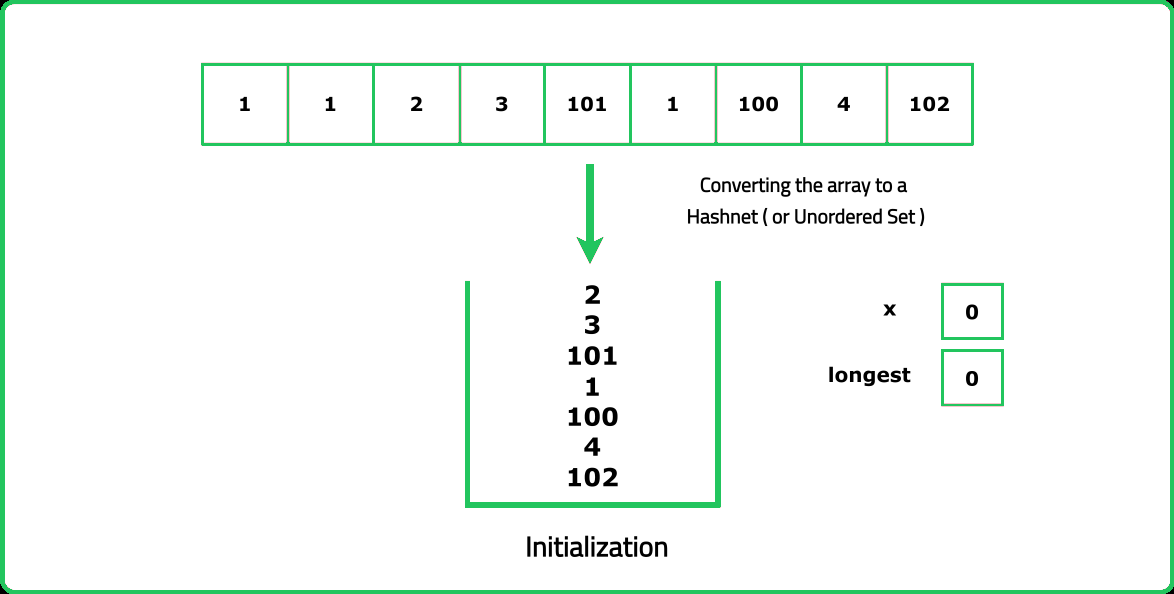
First, all array elements are placed into a set data structure.

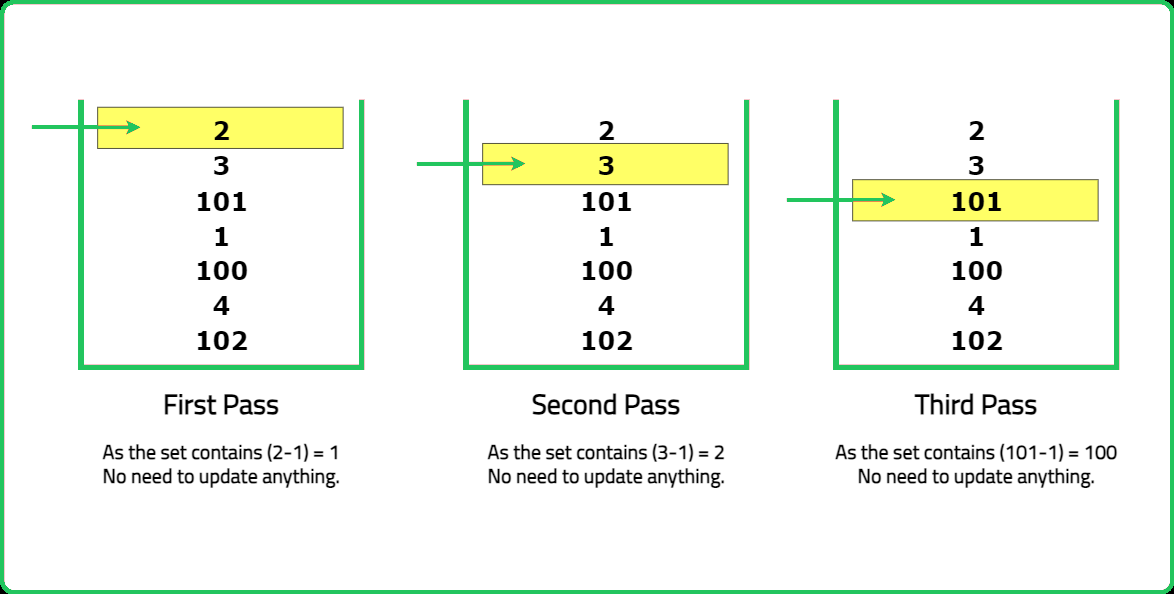
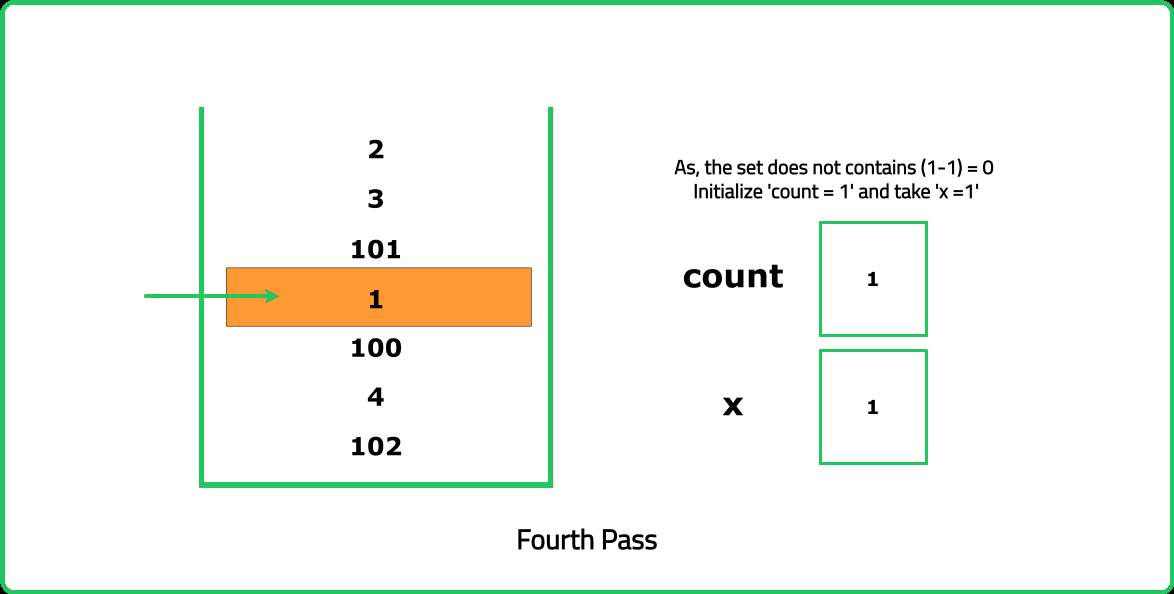
For each element x that can start a sequence (i.e., x - 1 does not exist in the set) we follow the below steps:

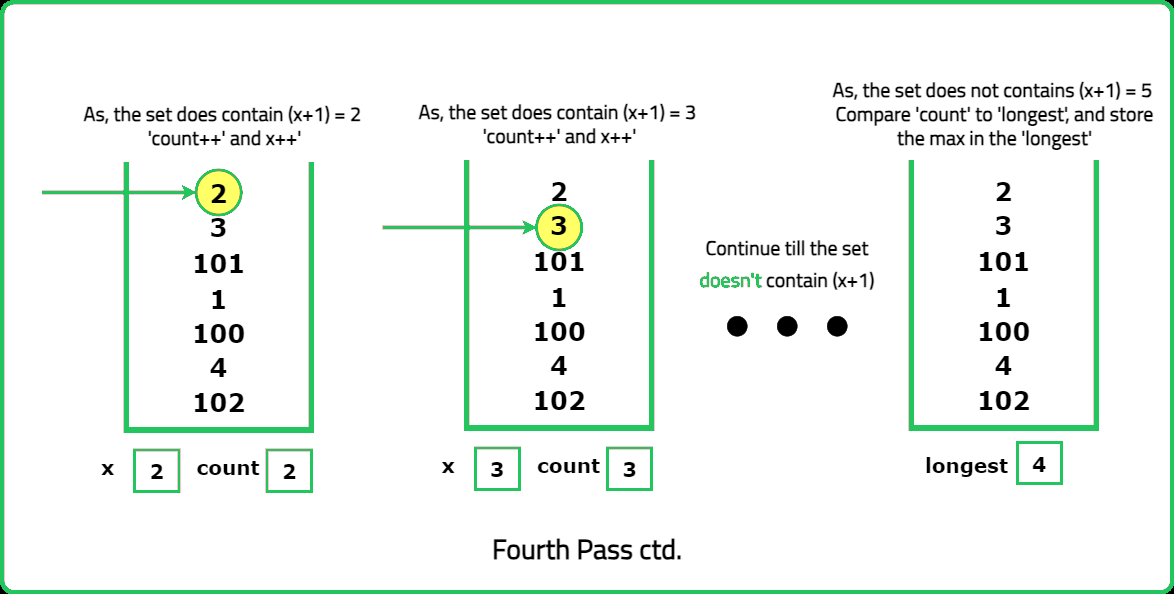
Initialize cnt to 1, indicating the starting element of a new sequence.
Utilize the set to search for consecutive elements such as x + 1, x + 2, and so on, to determine the maximum possible length of the current sequence. Update cnt accordingly.
Compare cnt with longest and update longest to hold the maximum value (longest = max(longest, cnt)).

Finally, longest will contain the length of the longest consecutive sequence found in the array.

Dry Run

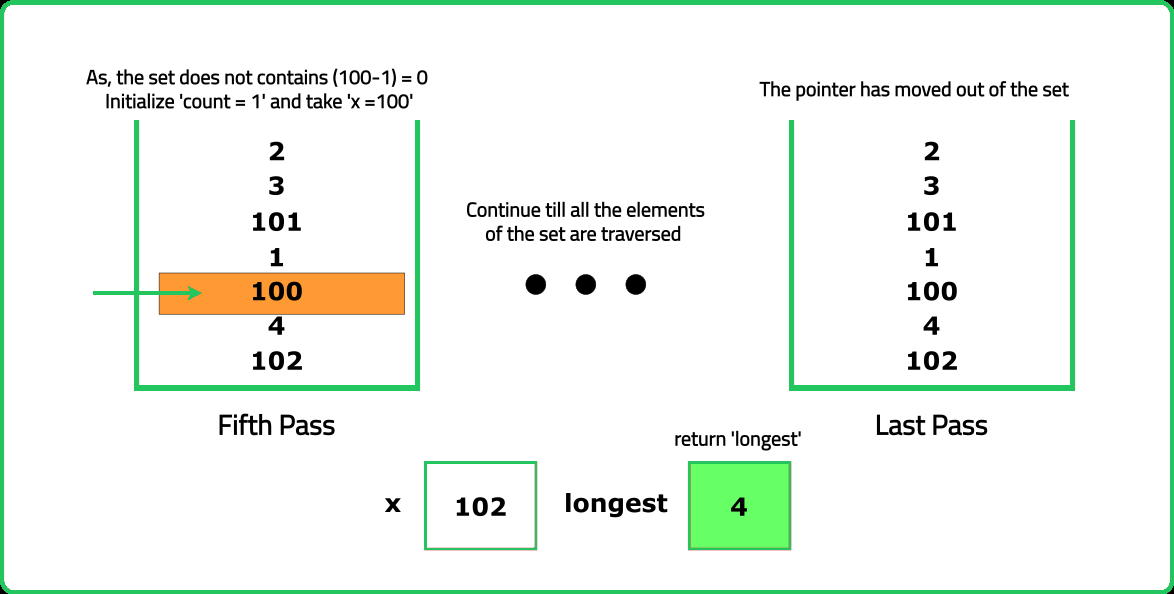
Please refer to the video for complete dry-run.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int longestConsecutive(vector<int>& a) {
        int n = a.size();
        // If the array is empty
        if (n == 0) return 0; 
    
        // Initialize the longest sequence length
        int longest = 1; 
        unordered_set<int> st;
    
        // Put all the array elements into the set
        for (int i = 0; i < n; i++) {
            st.insert(a[i]);
        }
    
        /* Traverse the set to 
           find the longest sequence  */
        for (auto it : st) {
            // Check if 'it' is a starting number of a sequence
            if (st.find(it - 1) == st.end()) {
                // Initialize the count of the current sequence
                int cnt = 1; 
                // Starting element of the sequence
                int x = it; 
    
                // Find consecutive numbers in the set
                while (st.find(x + 1) != st.end()) {
                    // Move to the next element in the sequence
                    x = x + 1; 
                    // Increment the count of the sequence
                    cnt = cnt + 1; 
                }
                // Update the longest sequence length
                longest = max(longest, cnt);
            }
        }
        return longest;
    }
};

int main() {
    vector<int> a = {100, 4, 200, 1, 3, 2}; 

    // Create an instance of solution class
    Solution solution; 
    // Function call for finding longest consecutive sequence
    int ans = solution.longestConsecutive(a); 
    cout << "The longest consecutive sequence is " << ans << "\n";
    return 0;
}

import java.util.*;

class Solution {
    public int longestConsecutive(int[] nums) {
        int n = nums.length;
        // If the array is empty
        if (n == 0) return 0;

        // Initialize the longest sequence length
        int longest = 1; 
        Set<Integer> st = new HashSet<>();

        // Put all the array elements into the set
        for (int i = 0; i < n; i++) {
            st.add(nums[i]);
        }

        /* Traverse the set to 
           find the longest sequence */
        for (int it : st) {
            // Check if 'it' is a starting number of a sequence
            if (!st.contains(it - 1)) {
                // Initialize the count of the current sequence
                int cnt = 1; 
                // Starting element of the sequence
                int x = it; 

                // Find consecutive numbers in the set
                while (st.contains(x + 1)) {
                    // Move to the next element in the sequence
                    x = x + 1; 
                    // Increment the count of the sequence
                    cnt = cnt + 1; 
                }
                // Update the longest sequence length
                longest = Math.max(longest, cnt);
            }
        }
        return longest;
    }

    public static void main(String[] args) {
        int[] a = {100, 4, 200, 1, 3, 2}; 
        // Create an instance of the solution class
        Solution solution = new Solution(); 
        // Function call to find the longest consecutive sequence
        int ans = solution.longestConsecutive(a); 
        System.out.println("The longest consecutive sequence is " + ans); 
    }
}
class Solution:
    def longestConsecutive(self, nums):
        n = len(nums)
        # If the array is empty
        if n == 0:
            return 0 

        # Initialize the longest sequence length
        longest = 1 
        st = set()

        # Put all the array elements into the set
        for i in range(n):
            st.add(nums[i])

        # Traverse the set to find the longest sequence
        for it in st:
            # Check if 'it' is a starting number of a sequence
            if it - 1 not in st:
                # Initialize the count of the current sequence
                cnt = 1 
                # Starting element of the sequence
                x = it 

                # Find consecutive numbers in the set
                while x + 1 in st:
                    # Move to the next element in the sequence
                    x = x + 1 
                    # Increment the count of the sequence
                    cnt = cnt + 1 
                # Update the longest sequence length
                longest = max(longest, cnt)
        return longest

if __name__ == "__main__":
    a = [100, 4, 200, 1, 3, 2] 
    # Create an instance of the solution class
    solution = Solution() 
    # Function call to find the longest consecutive sequence
    ans = solution.longestConsecutive(a) 
    print("The longest consecutive sequence is", ans)
class Solution {
    longestConsecutive(nums) {
        let n = nums.length;
        // If the array is empty
        if (n === 0) return 0;

        // Initialize the longest sequence length
        let longest = 1; 
        let st = new Set();

        // Put all the array elements into the set
        for (let i = 0; i < n; i++) {
            st.add(nums[i]);
        }

        // Traverse the set to find the longest sequence
        for (let it of st) {
            // Check if 'it' is a starting number of a sequence
            if (!st.has(it - 1)) {
                // Initialize the count of the current sequence
                let cnt = 1; 
                // Starting element of the sequence
                let x = it; 

                // Find consecutive numbers in the set
                while (st.has(x + 1)) {
                    // Move to the next element in the sequence
                    x = x + 1; 
                    // Increment the count of the sequence
                    cnt = cnt + 1; 
                }
                // Update the longest sequence length
                longest = Math.max(longest, cnt);
            }
        }
        return longest;
    }
}

// Sample array
const a = [100, 4, 200, 1, 3, 2]; 
// Create an instance of the solution class
const solution = new Solution(); 
// Function call to find the longest consecutive sequence
const ans = solution.longestConsecutive(a); 
console.log("The longest consecutive sequence is " + ans);

Complexity Analysis

Time Complexity: O(N) + O(2xN) ~ O(3xN), where N is the size of the array. The function takes O(N) to insert all elements into the set data structure. After that, for every starting element, we find the consecutive elements. Although nested loops are used, the set will be traversed at most twice in the worst case. Therefore, the time complexity is O(2xN) instead of O(N²). Space Complexity: O(N), as we use a set data structure to solve this problem.

Note: The time complexity assumes that we use an unordered_set, which has O(1) time complexity for set operations.

In the worst case, if the set operations take O(N), the total time complexity would be approximately O(N²). If we use a set instead of an unordered_set, the set operations will have a time complexity of O(logN), resulting in a total time complexity of O(NlogN).

Problem List

Longest Consecutive Sequence in an Array

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Complexity Analysis

Intuition

Approach

Complexity Analysis

Intuition

Approach

Dry Run

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code