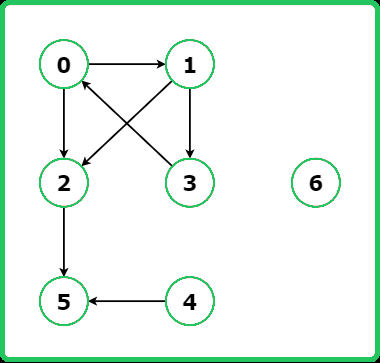
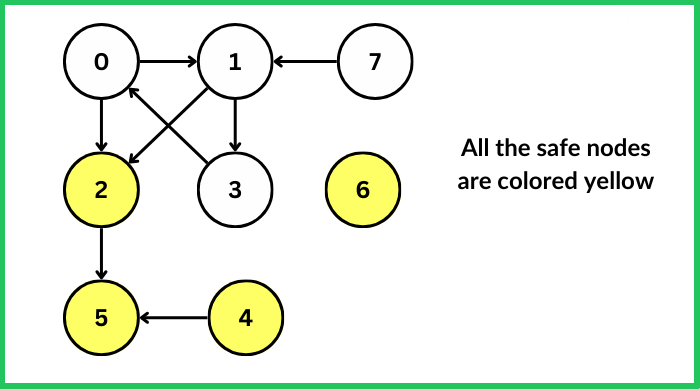
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to perform DFS traversal
while checking for safe nodes */
bool dfsCheck(int node, vector<int> adj[],
vector<int> &vis,
vector<int> &pathVis,
vector<int> &check) {
// Mark the node as visited
vis[node] = 1;
// Add the node to current path
pathVis[node] = 1;
// Mark the node as potentially unsafe
check[node] = 0;
// Traverse for adjacent nodes
for (auto it : adj[node]) {
// When the node is not visited
if (!vis[it]) {
/* Perform DFS recursively and if
a cycle is found, return false */
if (dfsCheck(it, adj, vis, pathVis, check)) {
/* Return true since a
cycle was detected */
return true;
}
}
/* Else if the node has been previously
visited in the same path*/
else if (pathVis[it]) {
/* Return true since a
cycle was detected */
return true;
}
}
/* If the current node neither exist
in a cycle nor points to a cycle,
it can be marked as a safe node */
check[node] = 1;
// Remove the node from the current path
pathVis[node] = 0;
// Return false since no cycle was found
return false;
}
public:
/* Function to get the
eventually safe nodes */
vector<int> eventualSafeNodes(int V,
vector<int> adj[]) {
// Visited array
vector<int> vis(V, false);
// Path Visited array
vector<int> pathVis(V, false);
// To keep a check of safe nodes
vector<int> check(V, false);
/* Traverse the graph and
check for safe nodes */
for (int i = 0; i < V; i++) {
if (!vis[i]) {
// Start DFS traversal
dfsCheck(i, adj, vis, pathVis, check);
}
}
// To store the result
vector<int> ans;
// Add the safe nodes to the result
for (int i = 0; i < V; i++) {
if (check[i] == 1)
ans.push_back(i);
}
// Return the result
return ans;
}
};
int main() {
int V = 7;
vector<int> adj[V] = {
{1,2},
{2,3},
{5},
{0},
{5},
{},
{}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to get the eventually
safe nodes in the given graph */
vector<int> ans = sol.eventualSafeNodes(V, adj);
// Output
cout << "The eventually safe nodes in the graph are:\n";
for(int i=0; i < ans.size(); i++) {
cout << ans[i] << " ";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class Solution {
/* Function to perform DFS traversal
while checking for safe nodes */
private boolean dfsCheck(int node, int[][] adj,
boolean[] vis,
boolean[] pathVis,
boolean[] check) {
// Mark the node as visited
vis[node] = true;
// Add the node to current path
pathVis[node] = true;
// Mark the node as potentially unsafe
check[node] = false;
// Traverse for adjacent nodes
for (int it : adj[node]) {
// When the node is not visited
if (!vis[it]) {
/* Perform DFS recursively and if
a cycle is found, return false */
if (dfsCheck(it, adj, vis, pathVis, check)) {
/* Return true since a
cycle was detected */
return true;
}
}
/* Else if the node has been previously
visited in the same path*/
else if (pathVis[it]) {
/* Return true since a
cycle was detected */
return true;
}
}
/* If the current node neither exist
in a cycle nor points to a cycle,
it can be marked as a safe node */
check[node] = true;
// Remove the node from the current path
pathVis[node] = false;
// Return false since no cycle was found
return false;
}
// Function to get the eventually safe nodes
public int[] eventualSafeNodes(int V, int[][] adj) {
// Visited array
boolean[] vis = new boolean[V];
// Path Visited array
boolean[] pathVis = new boolean[V];
// To keep a check of safe nodes
boolean[] check = new boolean[V];
/* Traverse the graph and
check for safe nodes */
for (int i = 0; i < V; i++) {
if (!vis[i]) {
// Start DFS traversal
dfsCheck(i, adj, vis, pathVis, check);
}
}
// To store the result
List<Integer> temp = new ArrayList<>();
// Add the safe nodes to the result
for (int i = 0; i < V; i++) {
if (check[i])
temp.add(i);
}
// Convert List to array
int[] ans = new int[temp.size()];
for (int i = 0; i < temp.size(); i++) {
ans[i] = temp.get(i);
}
// Return the result
return ans;
}
public static void main(String[] args) {
int V = 7;
int[][] adj = {
{1, 2},
{2, 3},
{5},
{0},
{5},
{},
{}
};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to get the eventually
safe nodes in the given graph */
int[] ans = sol.eventualSafeNodes(V, adj);
// Output
System.out.println("The eventually safe nodes in the graph are:");
for (int node : ans) {
System.out.print(node + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111
from typing import List
class Solution:
# Function to perform DFS traversal
# while checking for safe nodes
def dfsCheck(self, node: int, adj: List[List[int]],
vis: List[bool],
pathVis: List[bool],
check: List[bool]) -> bool:
# Mark the node as visited
vis[node] = True
# Add the node to current path
pathVis[node] = True
# Mark the node as potentially unsafe
check[node] = False
# Traverse for adjacent nodes
for it in adj[node]:
# When the node is not visited
if not vis[it]:
# Perform DFS recursively and if
# a cycle is found, return false
if self.dfsCheck(it, adj, vis, pathVis, check):
# Return true since a
# cycle was detected
return True
# Else if the node has been previously
# visited in the same path
elif pathVis[it]:
# Return true since a
# cycle was detected
return True
# If the current node neither exist
# in a cycle nor points to a cycle,
# it can be marked as a safe node
check[node] = True
# Remove the node from the current path
pathVis[node] = False
# Return false since no cycle was found
return False
# Function to get the eventually safe nodes
def eventualSafeNodes(self, V, adj):
# Visited array
vis = [False] * V
# Path Visited array
pathVis = [False] * V
# To keep a check of safe nodes
check = [False] * V
# Traverse the graph and
# check for safe nodes
for i in range(V):
if not vis[i]:
# Start DFS traversal
self.dfsCheck(i, adj, vis, pathVis, check)
# To store the result
ans = []
# Add the safe nodes to the result
for i in range(V):
if check[i]:
ans.append(i)
# Return the result
return ans
# Main function
if __name__ == "__main__":
V = 7
adj = [
[1,2],
[2,3],
[5],
[0],
[5],
[],
[]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to get the eventually
# safe nodes in the given graph
ans = sol.eventualSafeNodes(V, adj)
# Output
print("The eventually safe nodes in the graph are:")
for node in ans:
print(node, end=" ")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114
class Solution {
// Function to perform DFS traversal
// while checking for safe nodes
dfsCheck(node, adj, vis, pathVis, check) {
// Mark the node as visited
vis[node] = true;
// Add the node to current path
pathVis[node] = true;
// Mark the node as potentially unsafe
check[node] = false;
// Traverse for adjacent nodes
for (let it of adj[node]) {
// When the node is not visited
if (!vis[it]) {
// Perform DFS recursively and if
// a cycle is found, return false
if (this.dfsCheck(it, adj, vis, pathVis, check)) {
// Return true since a
// cycle was detected
return true;
}
}
// Else if the node has been previously
// visited in the same path
else if (pathVis[it]) {
// Return true since a
// cycle was detected
return true;
}
}
// If the current node neither exist
// in a cycle nor points to a cycle,
// it can be marked as a safe node
check[node] = true;
// Remove the node from the current path
pathVis[node] = false;
// Return false since no cycle was found
return false;
}
// Function to get the eventually safe nodes
eventualSafeNodes(V, adj) {
// Visited array
let vis = new Array(V).fill(false);
// Path Visited array
let pathVis = new Array(V).fill(false);
// To keep a check of safe nodes
let check = new Array(V).fill(false);
// Traverse the graph and
// check for safe nodes
for (let i = 0; i < V; i++) {
if (!vis[i]) {
// Start DFS traversal
this.dfsCheck(i, adj, vis, pathVis, check);
}
}
// To store the result
let ans = [];
// Add the safe nodes to the result
for (let i = 0; i < V; i++) {
if (check[i])
ans.push(i);
}
// Return the result
return ans;
}
}
// Main function
let V = 7;
let adj = [
[1,2],
[2,3],
[5],
[0],
[5],
[],
[]
];
// Creating an instance of
// Solution class
let sol = new Solution();
// Function call to get the eventually
// safe nodes in the given graph
let ans = sol.eventualSafeNodes(V, adj);
// Output
console.log("The eventually safe nodes in the graph are:");
for (let i = 0; i < ans.length; i++) {
console.log(ans[i] + " ");
}