Edit distance

For every index of string 'start'(S1), we have three options to match that index with string 'target'(S2), i.e replace the character, remove the character or insert some character at that index. Therefore, we can think in terms of string matching path as we have done already in previous questions. As there is no uniformity in data, there is no other way to find out than to try out all possible ways. To do so we will need to use recursion.

Steps to form the recursive solution:

Express the problem in terms of indexes: We are given two strings. We can represent them with the help of two indexes i and j. Initially, i=n-1 and j=m-1, where n and m are lengths of strings S1 and S2. Initially, we will call f(n-1,m-1), which means the minimum number of operations required to convert string S1[0…n-1] to string S2[0…m-1].

So, f(i, j) gives the minimum number of operations required to convert string S1[from index 0 to i] to S2[from index 0 to j].

Try out all possible choices at a given index:Now, i and j represent two characters from strings 'start' and 'target' respectively. There are only two options, either the characters represented by i and j match or they don’t.

When the characters match: If(S2[i] == S2[j]), we would not want to do any operations to make them match, so we will just decrement both i and j by 1 and recursively find the answer for the remaining string portion. Return 0+f(i-1,j-1).

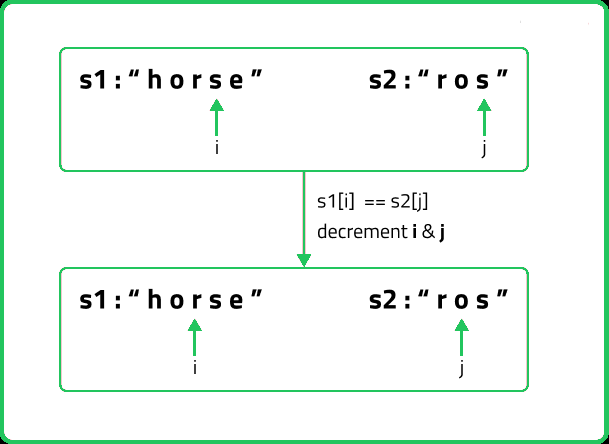
When the characters don’t match: If(S1[i] != S2[j]) is true, then we have to do any of three operations to match the characters. We have three options, we will analyze each of them one by one.

(Case 1)Inserting a character: Consider this example,

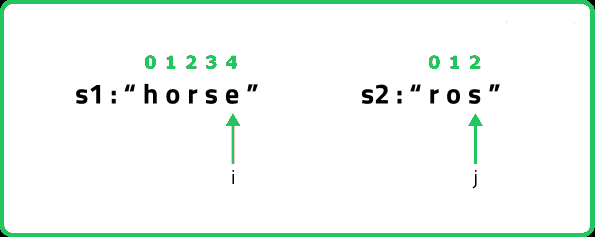
Now if we have to match the strings by insertions, what would we do:

We would have placed an ‘s’ at index 5 of S1.
Suppose i now point to s at index 5 of S1 and j points are already pointing to s at index j of S2.
Now, we hit the condition, where characters do match. (as mentioned in case 1).
Therefore, we will decrement i and j by 1. They will now point to index 4 and 1 respectively.

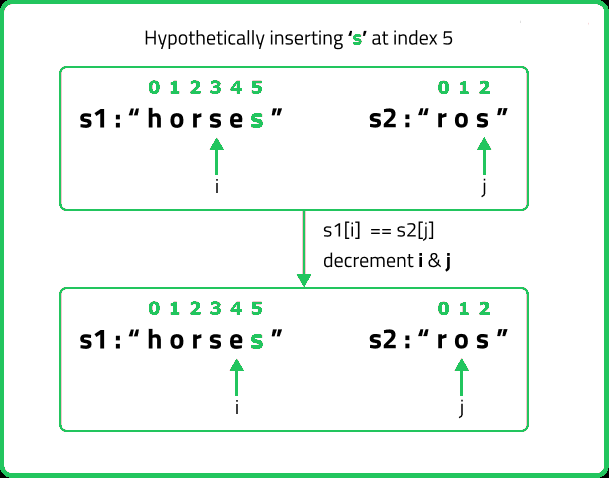
Now, the number of operations we did were only 1 (inserting s at index 5) but do we need to really insert the ‘s’ at index 5 and modify the string? The answer is simply NO. As we see that inserting a character (here ‘s’ at index 5), we will eventually get to the third step. So we can just return 1+ f(i,j-1) as i remains there only after insertion and j decrements by 1. We can say that we have hypothetically inserted character s.

(Case 2)Deleting a character: Consider the same example,

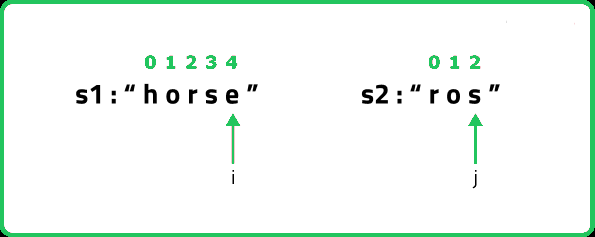
We can simply delete the character at index 4 and check from the next index.

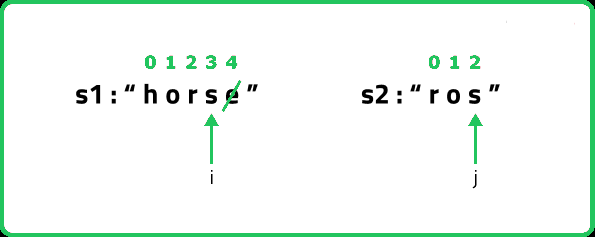
Now, j remains at its original index and we decrement i by 1. We perform 1 operation, therefore we will recursively call 1+f(i-1,j).

(Case 3)Replacing a character: Consider the same example,

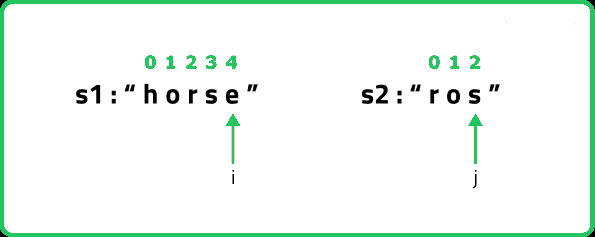
If we replace the character ‘e’ at index 4 of S1 with ‘s’, we have matched both the characters ourselves. We again hit the case of character matching, therefore we decrement both i and j by 1. As the number of operations performed is 1, we will return 1+f(i-1,j-1).

To summarise, these are the three choices we have in case characters don’t match:

In case of insertion of character, return 1+f(i-1,j).
In case of deletion of character, return 1+f(i,j-1).
In case of replacement of character, return 1+f(i-1,j-1).

/*It is pseudocode and it is not related 
to any specific programming language */
f(i, j){
    if(S1[i] == S2[j]){
        return f(i-1, j-1)
    }
     else
        return 1 + min(f(i-1, j-1), f(i-1, j), f(i, j-1))
}

Return the minimum of all choices: As we have to return the minimum number of operations, we will return the minimum of all operations.
Base Cases: We are reducing i and j in our recursive relation, there can be two possibilities, either i becomes -1 or j becomes -1., i,e we exhaust either S1 or S2 respectively.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to calculate the edit
    distance between two strings*/
    int editDistanceUtil(string& S1, string& S2, int i, int j) {
        // Base cases
        if (i < 0)
            return j + 1;
        if (j < 0)
            return i + 1;

        /* If the characters at the current
        positions match, no operation is needed*/
        if (S1[i] == S2[j]){
            return 0 + editDistanceUtil(S1, S2, i - 1, j - 1);
        }
        // Take minimum of three choices
        else{
            return 1 + min(editDistanceUtil(S1, S2, i - 1, j - 1),
                                  min(editDistanceUtil(S1, S2, i - 1, j),
                                      editDistanceUtil(S1, S2, i, j - 1)));
        }
    }
public:
    /* Function to calculate the minimum number 
    of operations required to transform S1 into S2*/
    int editDistance(string start, string target) {
        int n = start.size();
        int m = target.size();

        /* Call the utility function with 
        the last indices of both strings*/
        return editDistanceUtil(start, target, n - 1, m - 1);
    }
};

int main() {
    string s1 = "horse";
    string s2 = "ros";
    
    //Create an instance of Solutoin sol;
    Solution sol;

    // Call the editDistance function and print the result
    cout << "The minimum number of operations required is: " << sol.editDistance(s1, s2);
    return 0;
}

import java.util.*;

class Solution {
    /* Function to calculate the edit
    distance between two strings*/
    private int editDistanceUtil(String S1, String S2, int i, int j) {
        // Base cases
        if (i < 0)
            return j + 1;
        if (j < 0)
            return i + 1;

        /* If the characters at the current 
        positions match, no operation is needed*/
        if (S1.charAt(i) == S2.charAt(j)){
            return 0 + editDistanceUtil(S1, S2, i - 1, j - 1);
        }
        // Take minimum of three choices
        else {
            return 1 + Math.min(editDistanceUtil(S1, S2, i - 1, j - 1),
                                  Math.min(editDistanceUtil(S1, S2, i - 1, j),
                                           editDistanceUtil(S1, S2, i, j - 1)));
        }
    }
    
    /* Function to calculate the minimum number of 
    operations required to transform start into target*/
    public int editDistance(String start, String target) {
        int n = start.length();
        int m = target.length();

        /* Call the utility function with
        the last indices of both strings*/
        return editDistanceUtil(start, target, n - 1, m - 1);
    }

    public static void main(String[] args) {
        String s1 = "horse";
        String s2 = "ros";
        
        // Create an instance of Solution
        Solution sol = new Solution();

        // Call the editDistance function and print the result
        System.out.println("The minimum number of operations required is: " + sol.editDistance(s1, s2));
    }
}
class Solution:
    """ Function to calculate the edit
    distance between two strings"""
    def editDistanceUtil(self, S1, S2, i, j):
        # Base cases
        if i < 0:
            return j + 1
        if j < 0:
            return i + 1

        """ If the characters at the current
        positions match, no operation is needed"""
        if S1[i] == S2[j]:
            return 0 + self.editDistanceUtil(S1, S2, i - 1, j - 1)
        
        # Take minimum of three choices
        else:
            return 1 + min(self.editDistanceUtil(S1, S2, i - 1, j - 1),
                                  min(self.editDistanceUtil(S1, S2, i - 1, j),
                                      self.editDistanceUtil(S1, S2, i, j - 1)))

    """ Function to calculate the minimum number of
    operations required to transform start into target"""
    def editDistance(self, start, target):
        n = len(start)
        m = len(target)

        """ Call the utility function with 
        the last indices of both strings"""
        return self.editDistanceUtil(start, target, n - 1, m - 1)

if __name__ == "__main__":
    s1 = "horse"
    s2 = "ros"
    
    # Create an instance of Solution
    sol = Solution()

    # Call the editDistance function and print the result
    print("The minimum number of operations required is:", sol.editDistance(s1, s2))
class Solution {
    /* Function to calculate the edit
    distance between two strings*/
    editDistanceUtil(S1, S2, i, j) {
        // Base cases
        if (i < 0) return j + 1;
        if (j < 0) return i + 1;

        /* If the characters at the current
        positions match, no operation is needed*/
        if (S1.charAt(i) === S2.charAt(j)) {
            return 0 + this.editDistanceUtil(S1, S2, i - 1, j - 1);
        }
        // Take minimum of three choices
        else {
            return 1 + Math.min(this.editDistanceUtil(S1, S2, i - 1, j - 1),
                                  Math.min(this.editDistanceUtil(S1, S2, i - 1, j),
                                           this.editDistanceUtil(S1, S2, i, j - 1)));
        }
    }
    /* Function to calculate the minimum number of
    operations required to transform start into target*/
    editDistance(start, target) {
        const n = start.length;
        const m = target.length;

        /* Call the utility function with
        the last indices of both strings*/
        return this.editDistanceUtil(start, target, n - 1, m - 1);
    }
}

const s1 = "horse";
const s2 = "ros";

// Create an instance of Solution
const sol = new Solution();

// Call the editDistance function and print the result
console.log("The minimum number of operations required is:", sol.editDistance(s1, s2));

Complexity Analysis:

Time Complexity: Exponential .

Space Complexity: O(N+M), where N is the length of string S1 and M is the length of string S2. As we are using a recursion stack space(O(N+M)).

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

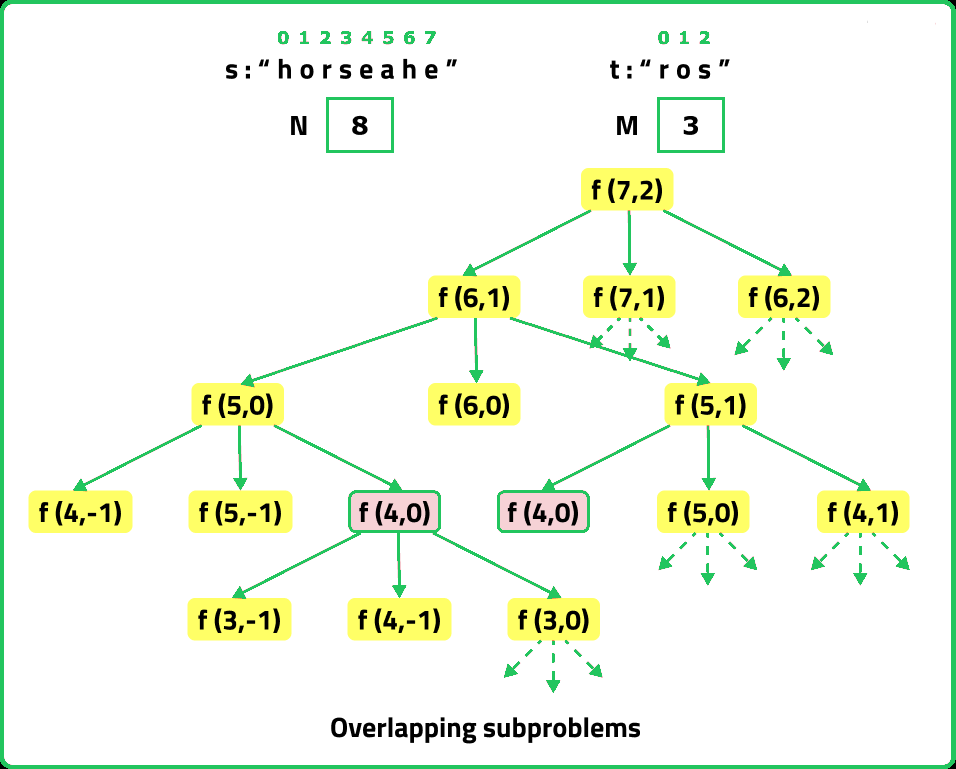
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][m]: where n and m are the lengths of 'S1' and 'S2' respectively. As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is (n-1) and 'j' can attain maximum value of (m-1). Therefore, we need 2D dp array.

The dp array shows the calculations of the subproblems, initialize it with -1 to show that no subproblem is solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to calculate the edit
    distance between two strings*/
    int editDistanceUtil(string& S1, string& S2, int i, int j, vector<vector<int>>& dp) {
        // Base cases
        if (i < 0)
            return j + 1;
        if (j < 0)
            return i + 1;

        /* If the result for this state has
        already been calculated, return it*/
        if (dp[i][j] != -1)
            return dp[i][j];

        /* If the characters at the current
        positions match, no operation is needed*/
        if (S1[i] == S2[j]){
            return dp[i][j] = 0 + editDistanceUtil(S1, S2, i - 1, j - 1, dp);
        }
        // Take minimum of three choices
        else{
            return dp[i][j] = 1 + min(editDistanceUtil(S1, S2, i - 1, j - 1, dp),
                                  min(editDistanceUtil(S1, S2, i - 1, j, dp),
                                      editDistanceUtil(S1, S2, i, j - 1, dp)));
        }
    }
public:
    /* Function to calculate the minimum number 
    of operations required to transform S1 into S2*/
    int editDistance(string start, string target) {
        int n = start.size();
        int m = target.size();

        // Create a DP table to memoize results
        vector<vector<int>> dp(n, vector<int>(m, -1));

        /* Call the utility function with 
        the last indices of both strings*/
        return editDistanceUtil(start, target, n - 1, m - 1, dp);
    }
};

int main() {
    string s1 = "horse";
    string s2 = "ros";
    
    //Create an instance of Solutoin sol;
    Solution sol;

    // Call the editDistance function and print the result
    cout << "The minimum number of operations required is: " << sol.editDistance(s1, s2);
    return 0;
}

import java.util.*;

class Solution {
    /* Function to calculate the edit
    distance between two strings*/
    private int editDistanceUtil(String S1, String S2, int i, int j, int[][] dp) {
        // Base cases
        if (i < 0)
            return j + 1;
        if (j < 0)
            return i + 1;

        /* If the result for this state has
        already been calculated, return it*/
        if (dp[i][j] != -1)
            return dp[i][j];

        /* If the characters at the current 
        positions match, no operation is needed*/
        if (S1.charAt(i) == S2.charAt(j)){
            return dp[i][j] = 0 + editDistanceUtil(S1, S2, i - 1, j - 1, dp);
        }
        // Take minimum of three choices
        else {
            return dp[i][j] = 1 + Math.min(editDistanceUtil(S1, S2, i - 1, j - 1, dp),
                                  Math.min(editDistanceUtil(S1, S2, i - 1, j, dp),
                                           editDistanceUtil(S1, S2, i, j - 1, dp)));
        }
    }
    
    /* Function to calculate the minimum number of 
    operations required to transform start into target*/
    public int editDistance(String start, String target) {
        int n = start.length();
        int m = target.length();

        // Create a DP table to memoize results
        int[][] dp = new int[n][m];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        /* Call the utility function with
        the last indices of both strings*/
        return editDistanceUtil(start, target, n - 1, m - 1, dp);
    }

    public static void main(String[] args) {
        String s1 = "horse";
        String s2 = "ros";
        
        // Create an instance of Solution
        Solution sol = new Solution();

        // Call the editDistance function and print the result
        System.out.println("The minimum number of operations required is: " + sol.editDistance(s1, s2));
    }
}
class Solution:
    """ Function to calculate the edit
    distance between two strings"""
    def editDistanceUtil(self, S1, S2, i, j, dp):
        # Base cases
        if i < 0:
            return j + 1
        if j < 0:
            return i + 1

        """ If the result for this state has 
        already been calculated, return it"""
        if dp[i][j] != -1:
            return dp[i][j]

        """ If the characters at the current
        positions match, no operation is needed"""
        if S1[i] == S2[j]:
            dp[i][j] = 0 + self.editDistanceUtil(S1, S2, i - 1, j - 1, dp)
            return dp[i][j]
        # Take minimum of three choices
        else:
            dp[i][j] = 1 + min(self.editDistanceUtil(S1, S2, i - 1, j - 1, dp),
                                  min(self.editDistanceUtil(S1, S2, i - 1, j, dp),
                                      self.editDistanceUtil(S1, S2, i, j - 1, dp)))
            return dp[i][j]

    """ Function to calculate the minimum number of
    operations required to transform start into target"""
    def editDistance(self, start, target):
        n = len(start)
        m = len(target)

        # Create a DP table to memoize results
        dp = [[-1] * m for _ in range(n)]

        """ Call the utility function with 
        the last indices of both strings"""
        return self.editDistanceUtil(start, target, n - 1, m - 1, dp)

if __name__ == "__main__":
    s1 = "horse"
    s2 = "ros"
    
    # Create an instance of Solution
    sol = Solution()

    # Call the editDistance function and print the result
    print("The minimum number of operations required is:", sol.editDistance(s1, s2))
class Solution {
    /* Function to calculate the edit
    distance between two strings*/
    editDistanceUtil(S1, S2, i, j, dp) {
        // Base cases
        if (i < 0) return j + 1;
        if (j < 0) return i + 1;

        /* If the result for this state has
        already been calculated, return it*/
        if (dp[i][j] !== -1) return dp[i][j];

        /* If the characters at the current
        positions match, no operation is needed*/
        if (S1.charAt(i) === S2.charAt(j)) {
            dp[i][j] = 0 + this.editDistanceUtil(S1, S2, i - 1, j - 1, dp);
            return dp[i][j];
        }
        // Take minimum of three choices
        else {
            dp[i][j] = 1 + Math.min(this.editDistanceUtil(S1, S2, i - 1, j - 1, dp),
                                  Math.min(this.editDistanceUtil(S1, S2, i - 1, j, dp),
                                           this.editDistanceUtil(S1, S2, i, j - 1, dp)));
            return dp[i][j];
        }
    }
    /* Function to calculate the minimum number of
    operations required to transform start into target*/
    editDistance(start, target) {
        const n = start.length;
        const m = target.length;

        // Create a DP table to memoize results
        const dp = Array.from({ length: n }, () => Array(m).fill(-1));

        /* Call the utility function with
        the last indices of both strings*/
        return this.editDistanceUtil(start, target, n - 1, m - 1, dp);
    }
}

const s1 = "horse";
const s2 = "ros";

// Create an instance of Solution
const sol = new Solution();

// Call the editDistance function and print the result
console.log("The minimum number of operations required is:", sol.editDistance(s1, s2));

Complexity Analysis: Time Complexity: O(NM), where N is the length of string S1 and M is the length of string S2. There are NM states therefore at max ‘NM’ new problems will be solved.

Space Complexity: O(N+M) + O(NM), Where N is the length of string S1 and M is the length of S2. As we are using a recursion stack space(O(N+M)) and an array of size N*M.

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n][m]: where n and m are the lengths of 's' and 't' respectively. As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is (n-1) and 'j' can attain maximum value of (m-1). Therefore, we need 2D dp array.
Setting Base Cases in the Array: In the recursive code, our base condition was when i < 0 or j < 0, but we can’t set the dp array’s index to -1. Therefore a hack for this issue is to shift every index by 1 towards the right.

Therefore, we set the base condition (keep in mind 1-based indexing), we set the first column’s value as 1 and the first row as 1.

Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations. Keeping in mind the shifting of indexes, as for example str1[ind1] will be converted to str1[ind1-1].
Returning the answer: At last dp[n][m] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to calculate the minimum number 
    of operations required to transform S1 into S2*/
    int editDistance(string start, string target) {
        int n = start.size();
        int m = target.size();

        // Create a DP table to store edit distances
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));

        // Initialize the first row and column
        for (int i = 0; i <= n; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j <= m; j++) {
            dp[0][j] = j;
        }

        // Fill in the DP table
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                // If characters match, no additional cost
                if (start[i - 1] == target[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } 
                // Take minimum of three choices
                else {
                    dp[i][j] = 1 + min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1]));
                }
            }
        }

        // The value at dp[n][m] contains the edit distance
        return dp[n][m];
    }
};

int main() {
    string s1 = "horse";
    string s2 = "ros";
    
    //Create an instance of Solutoin sol;
    Solution sol;

    // Call the editDistance function and print the result
    cout << "The minimum number of operations required is: " << sol.editDistance(s1, s2);
    return 0;
}

import java.util.*;

class Solution {
    /* Function to calculate the minimum number 
    of operations required to transform start into target */
    public int editDistance(String start, String target) {
        int n = start.length();
        int m = target.length();

        // Create a DP table to store edit distances
        int[][] dp = new int[n + 1][m + 1];

        // Initialize the first row and column
        for (int i = 0; i <= n; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j <= m; j++) {
            dp[0][j] = j;
        }

        // Fill in the DP table
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                // If characters match, no additional cost
                if (start.charAt(i - 1) == target.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } 
                // Take minimum of three choices
                else {
                    dp[i][j] = 1 + Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1]));
                }
            }
        }

        // The value at dp[n][m] contains the edit distance
        return dp[n][m];
    }

    public static void main(String[] args) {
        String s1 = "horse";
        String s2 = "ros";
        
        // Create an instance of Solution
        Solution sol = new Solution();

        // Call the editDistance function and print the result
        System.out.println("The minimum number of operations required is: " + sol.editDistance(s1, s2));
    }
}
class Solution:
    """ Function to calculate the minimum number of 
    operations required to transform start into target"""
    def editDistance(self, start, target):
        n = len(start)
        m = len(target)

        # Create a DP table to store edit distances
        dp = [[0] * (m + 1) for _ in range(n + 1)]

        # Initialize the first row and column
        for i in range(n + 1):
            dp[i][0] = i
        for j in range(m + 1):
            dp[0][j] = j

        # Fill in the DP table
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                # If characters match, no additional cost
                if start[i - 1] == target[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    # Take minimum of three choices
                    dp[i][j] = 1 + min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1]))

        # The value at dp[n][m] contains the edit distance
        return dp[n][m]

if __name__ == "__main__":
    s1 = "horse"
    s2 = "ros"
    
    # Create an instance of Solution
    sol = Solution()

    # Call the editDistance function and print the result
    print("The minimum number of operations required is:", sol.editDistance(s1, s2))
class Solution {
    /* Function to calculate the minimum number 
    of operations required to transform start into target */
    editDistance(start, target) {
        const n = start.length;
        const m = target.length;

        // Create a DP table to store edit distances
        const dp = Array.from({ length: n + 1 }, () => Array(m + 1).fill(0));

        // Initialize the first row and column
        for (let i = 0; i <= n; i++) {
            dp[i][0] = i;
        }
        for (let j = 0; j <= m; j++) {
            dp[0][j] = j;
        }

        // Fill in the DP table
        for (let i = 1; i <= n; i++) {
            for (let j = 1; j <= m; j++) {
                // If characters match, no additional cost
                if (start[i - 1] === target[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } 
                // Take minimum of three choices
                else {
                    dp[i][j] = 1 + Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1]));
                }
            }
        }

        // The value at dp[n][m] contains the edit distance
        return dp[n][m];
    }
}

const s1 = "horse";
const s2 = "ros";

// Create an instance of Solution
const sol = new Solution();

// Call the editDistance function and print the result
console.log("The minimum number of operations required is:", sol.editDistance(s1, s2));

Complexity Analysis: Time Complexity: O(NM), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(NM), Where N is the length of string S1 and M is the length of S2. As we are using an array of size N*M.

If we observe the relation obtained in the tabulation approach, dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]). We see that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.

We will space optimize in the following way:

Take two rows ‘prev’ and ‘cur’ and initialize it to the base condition.
Now, at starting the prev row needs to be initialized with its column value. Moreover, the cur variable whenever declared should have its first cell as a row value.
Next, implement the memoization logic and replace dp[i-1] with prev and dp[i] by cur in the tabulation code.
After every inner loop execution, we set prev=cur, for the next iteration.
At last, return prev[m] as our answer

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to calculate the minimum number 
    of operations required to transform S1 into S2*/
    int editDistance(string start, string target) {
        int n = start.size();
        int m = target.size();

        /* Declare two arrays to store previous
        and current row of edit distances*/
        vector<int> prev(m + 1, 0);
        vector<int> cur(m + 1, 0);

        // Initialize the first row
        for (int j = 0; j <= m; j++) {
            prev[j] = j;
        }

        // Calculate edit distances row by row
        for (int i = 1; i <= n; i++) {
            // Initialize the first column of current row
            cur[0] = i; 
            for (int j = 1; j <= m; j++) {
                // If the characters match, no additional cost
                if (start[i - 1] == target[j - 1]) {
                    cur[j] = prev[j - 1];
                } 
                else {
                    // Take minimum of three choices:
                    cur[j] = 1 + min(prev[j - 1], min(prev[j], cur[j - 1]));
                }
            }
            // Update the previous row with current row
            prev = cur; 
        }

        // The value at cur[m] contains the edit distance
        return cur[m];
    }
};

int main() {
    string s1 = "horse";
    string s2 = "ros";
    
    //Create an instance of Solutoin sol;
    Solution sol;

    // Call the editDistance function and print the result
    cout << "The minimum number of operations required is: " << sol.editDistance(s1, s2);
    return 0;
}

import java.util.*;

class Solution {
    /* Function to calculate the minimum number 
    of operations required to transform start into target */
    public int editDistance(String start, String target) {
        int n = start.length();
        int m = target.length();

        /* Declare two arrays to store previous
        and current row of edit distances */
        int[] prev = new int[m + 1];
        int[] cur = new int[m + 1];

        // Initialize the first row
        for (int j = 0; j <= m; j++) {
            prev[j] = j;
        }

        // Calculate edit distances row by row
        for (int i = 1; i <= n; i++) {
            // Initialize the first column of current row
            cur[0] = i;
            for (int j = 1; j <= m; j++) {
                // If the characters match, no additional cost
                if (start.charAt(i - 1) == target.charAt(j - 1)) {
                    cur[j] = prev[j - 1];
                } else {
                    // Take minimum of three choices
                    cur[j] = 1 + Math.min(prev[j - 1], Math.min(prev[j], cur[j - 1]));
                }
            }
            // Update the previous row with current row
            System.arraycopy(cur, 0, prev, 0, m + 1);
        }

        // The value at cur[m] contains the edit distance
        return cur[m];
    }

    public static void main(String[] args) {
        String s1 = "horse";
        String s2 = "ros";

        // Create an instance of Solution
        Solution sol = new Solution();

        // Call the editDistance function and print the result
        System.out.println("The minimum number of operations required is: " + sol.editDistance(s1, s2));
    }
}
class Solution:
    """ Function to calculate the minimum number of
    operations required to transform start into target"""
    def editDistance(self, start, target):
        n = len(start)
        m = len(target)

        """Declare two arrays to store previous
        and current row of edit distances"""
        prev = [0] * (m + 1)
        cur = [0] * (m + 1)

        # Initialize the first row
        for j in range(m + 1):
            prev[j] = j

        # Calculate edit distances row by row
        for i in range(1, n + 1):
            # Initialize the first column of current row
            cur[0] = i
            for j in range(1, m + 1):
                # If the characters match, no additional cost
                if start[i - 1] == target[j - 1]:
                    cur[j] = prev[j - 1]
                else:
                    # Take minimum of three choices
                    cur[j] = 1 + min(prev[j - 1], min(prev[j], cur[j - 1]))

            # Update the previous row with current row
            prev[:] = cur[:]

        # The value at cur[m] contains the edit distance
        return cur[m]

if __name__ == "__main__":
    s1 = "horse"
    s2 = "ros"

    # Create an instance of Solution
    sol = Solution()

    # Call the editDistance function and print the result
    print("The minimum number of operations required is:", sol.editDistance(s1, s2))
class Solution {
    /* Function to calculate the minimum number 
    of operations required to transform start into target */
    editDistance(start, target) {
        const n = start.length;
        const m = target.length;

        /* Declare two arrays to store previous
        and current row of edit distances */
        const prev = new Array(m + 1).fill(0);
        const cur = new Array(m + 1).fill(0);

        // Initialize the first row
        for (let j = 0; j <= m; j++) {
            prev[j] = j;
        }

        // Calculate edit distances row by row
        for (let i = 1; i <= n; i++) {
            // Initialize the first column of current row
            cur[0] = i;
            for (let j = 1; j <= m; j++) {
                // If the characters match, no additional cost
                if (start[i - 1] === target[j - 1]) {
                    cur[j] = prev[j - 1];
                } else {
                    // Take minimum of three choices
                    cur[j] = 1 + Math.min(prev[j - 1], Math.min(prev[j], cur[j - 1]));
                }
            }
            // Update the previous row with current row
            for (let k = 0; k <= m; k++) {
                prev[k] = cur[k];
            }
        }

        // The value at cur[m] contains the edit distance
        return cur[m];
    }
}

const s1 = "horse";
const s2 = "ros";

// Create an instance of Solution
const sol = new Solution();

// Call the editDistance function and print the result
console.log("The minimum number of operations required is:", sol.editDistance(s1, s2));

Complexity Analysis: Time Complexity: O(N*M), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(M), Where N is the length of string S1 and M is the length of S2. As we are using arrays of size M+1.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis: Time Complexity: O(NM), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(NM), Where N is the length of string S1 and M is the length of S2. As we are using an array of size N*M.

Complexity Analysis: Time Complexity: O(N*M), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(M), Where N is the length of string S1 and M is the length of S2. As we are using arrays of size M+1.

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Problem List

Edit distance

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis: Time Complexity: O(N*M), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem. Space Complexity: O(N*M), Where N is the length of string S1 and M is the length of S2. As we are using an array of size N*M.

Complexity Analysis: Time Complexity: O(N*M), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem. Space Complexity: O(M), Where N is the length of string S1 and M is the length of S2. As we are using arrays of size M+1.

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Complexity Analysis: Time Complexity: O(NM), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(NM), Where N is the length of string S1 and M is the length of S2. As we are using an array of size N*M.

Complexity Analysis: Time Complexity: O(N*M), where N is the length of string S1 and M is the length of string S2. There are two nested loops used to solve this problem.

Space Complexity: O(M), Where N is the length of string S1 and M is the length of S2. As we are using arrays of size M+1.