Making a large island

Intuition:

In the given grid, there are different sizes of connected 1s already present. The problem allows converting a single cell containing 0 to 1, and the goal is to form the largest island.

One way to solve this is by using the brute force approach by finding the largest island formed in the grid by successively converting each cell containing 0 to 1. The largest island found in all such cases will be the island with the most 1s which can be returned as our answer.

Understanding:

As each time, a cell having 0 is turned into 1, it forms an edge with its four neighbors(islands), if existing. This indicates that the graph is dynamic in nature. Now, adding an edge in a dynamic graph can be easily achieved using the Disjoint Set data structure.
Using the Union By Size method in the Disjoint Set data structure, not only the efficient addition of edges can be done but also, the size of islands after merging can be found.

How to store cells as nodes in the Disjoint Set?

The cells can be numbered sequentially as shown in the following figure: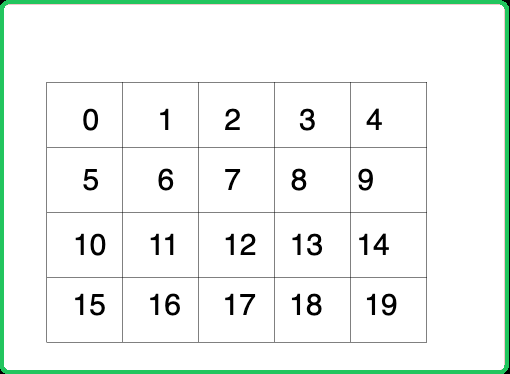

Thus, a number can be assigned to a cell having coordinates (i, j) in the following way:
Node number = i*n + j, where n is the number of columns in the grid

Edge Cases:

Consider the following graph:

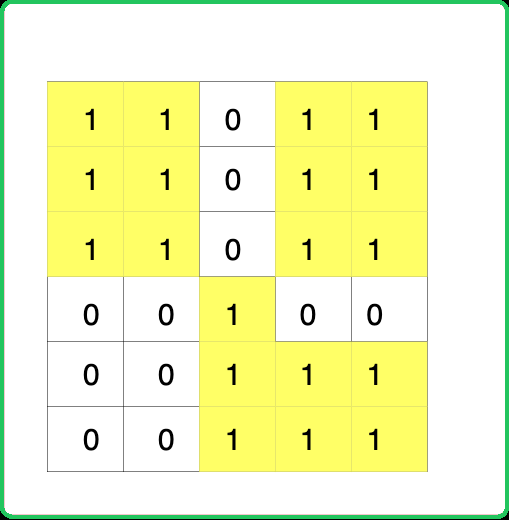
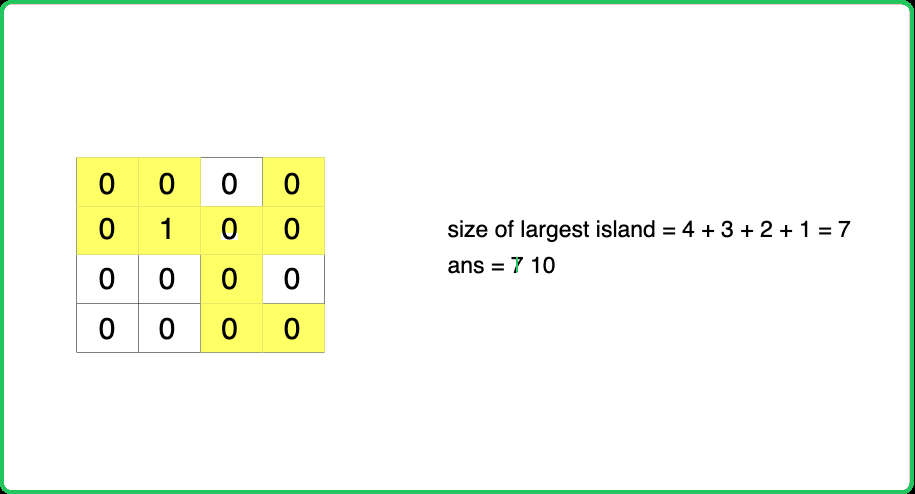
In the given grid, all the cells with 0 will be converted one by one to check for the largest island. Considering 0-based indexing, the cell (3,3) will be converted to 1, and while checking:

Left Island: The size of island will be incremented by 7.
Top Island: The size of island will be incremented by 6.
Right Island: No change in the size of the island as there is no island present on the right.
Bottom Island: Again the size of the island will be incremented by 7.

But the island of size 7 should have been considered only once while finding the size of the large island. This case can be avoided by storing the ultimate parents for the neighboring islands in a set data structure. This will ensure that one island will never be considered more than once in the size of large island.

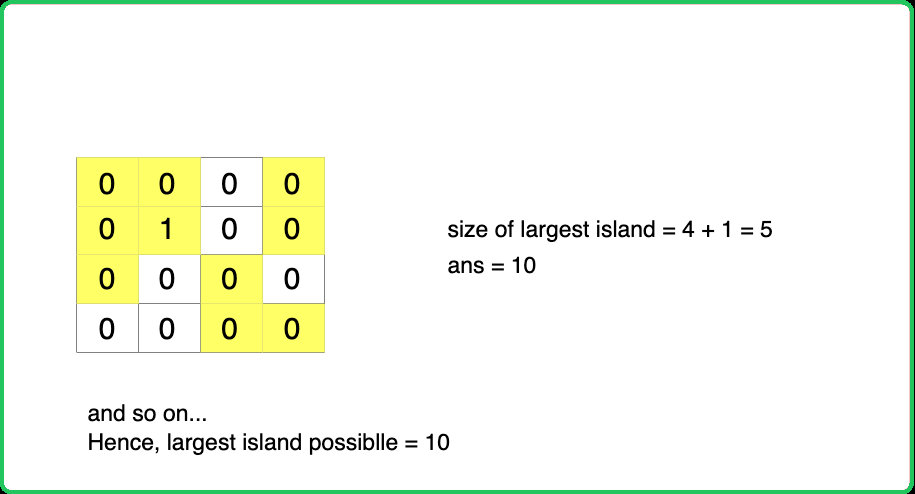
What if all the cells are 1 in the grid?

In such case, only one island will be formed which will be the largest for which the size of the ultimate parent of the island can be returned as the answer.

Approach:

Create a Disjoint Set data structure to manage connected components (islands) in the grid. Each cell is treated as a separate component initially.
Traverse through the grid to identify initial islands (connected 1s) and perform union operations to merge adjacent land cells into the same component using the union by size method.
Traverse the grid again to consider each 0 cell, and determine the potential island size if this 0 is changed to 1.
For each 0 cell, check all its neighboring cells to find unique components (using ultimate parents) and calculate the combined size of these components.
Keep track of the maximum island size encountered during the above calculations. Additionally, handle edge cases where no 0 cells are present in the grid by checking the sizes of existing islands.
Return the size of the largest possible island after changing at most one 0 to 1.

Dry Run:

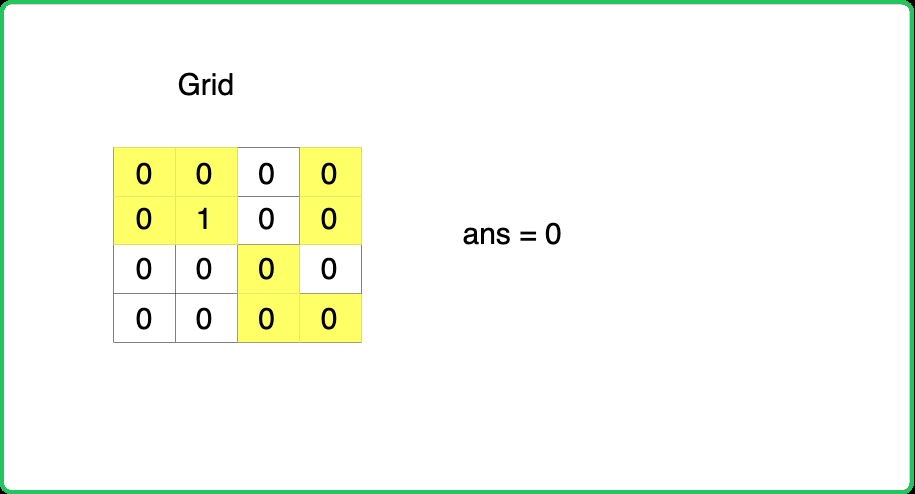
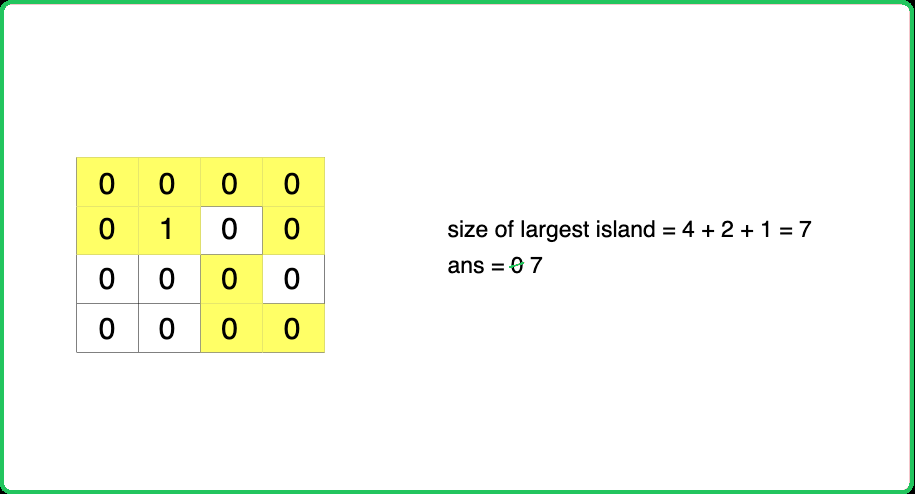
Solution:

#include <bits/stdc++.h>
using namespace std;

class DisjointSet {
public:
    /* To store the ranks, parents and 
    sizes of different set of vertices */
    vector<int> rank, parent, size;

    // Constructor
    DisjointSet(int n) {
        rank.resize(n + 1, 0);
        parent.resize(n + 1);
        size.resize(n + 1);
        for (int i = 0; i <= n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    
    // Function to find ultimate parent
    int findUPar(int node) {
        if (node == parent[node])
            return node;
        return parent[node] = findUPar(parent[node]);
    }
    
    // Function to implement union by rank
    void unionByRank(int u, int v) {
        int ulp_u = findUPar(u);
        int ulp_v = findUPar(v);
        if (ulp_u == ulp_v) return;
        if (rank[ulp_u] < rank[ulp_v]) {
            parent[ulp_u] = ulp_v;
        }
        else if (rank[ulp_v] < rank[ulp_u]) {
            parent[ulp_v] = ulp_u;
        }
        else {
            parent[ulp_v] = ulp_u;
            rank[ulp_u]++;
        }
    }
    
    // Function to implement union by size
    void unionBySize(int u, int v) {
        int ulp_u = findUPar(u);
        int ulp_v = findUPar(v);
        if (ulp_u == ulp_v) return;
        if (size[ulp_u] < size[ulp_v]) {
            parent[ulp_u] = ulp_v;
            size[ulp_v] += size[ulp_u];
        }
        else {
            parent[ulp_v] = ulp_u;
            size[ulp_u] += size[ulp_v];
        }
    }
};

// Solution class
class Solution{
private:
    // DelRow and delCol for neighbors
    vector<int> delRow = {-1, 0, 1, 0};
    vector<int> delCol = {0, 1, 0, -1};
    
    /* Helper Function to check if a 
    pixel is within boundaries */
    bool isValid(int &i, int &j, int &n) {
        
        // Return false if pixel is invalid
        if(i < 0 || i >= n) return false;
        if(j < 0 || j >= n) return false;
        
        // Return true if pixel is valid
        return true;
    }
    
    /* Function to add initial islands to 
    the disjoint set data structure */
    void addInitialIslands(vector<vector<int>> grid, 
                           DisjointSet &ds, int n) {
    
        // Traverse all the cells in the grid
        for (int row = 0; row < n ; row++) {
            for (int col = 0; col < n ; col++) {
                
                // If the cell is not land, skip
                if (grid[row][col] == 0) continue;
                
                // Traverse on all the neighbors
                for (int ind = 0; ind < 4; ind++) {
                    
                    // Get the coordinates of neighbor
                    int newRow = row + delRow[ind];
                    int newCol = col + delCol[ind];
                    
                    // If the cell is valid and a land cell
                    if (isValid(newRow, newCol, n) && 
                        grid[newRow][newCol] == 1) {
                            
                        // Get the number for node
                        int nodeNo = row * n + col;
                        // Get the number for neighbor
                        int adjNodeNo = newRow * n + newCol;
                        
                        /* Take union of both nodes as they
                        are part of the same island */
                        ds.unionBySize(nodeNo, adjNodeNo);
                    }
                }
            }
        }
    }
    
public:

    // Function to get the size of the largest island
    int largestIsland(vector<vector<int>>& grid) {
        
        // Dimensions of grid
        int n = grid.size();
        
        // Disjoint Set data structure
        DisjointSet ds(n*n);
        
        /* Function call to add initial 
        islands in the disjoint set */
        addInitialIslands(grid, ds, n);
        
        // To store the answer
        int ans = 0;
        
        // Traverse on the grid
        for (int row = 0; row < n; row++) {
            for (int col = 0; col < n; col++) {
                
                // If the cell is a land cell, skip
                if (grid[row][col] == 1) continue;
                
                /* Set to store the ultimate parents 
                of neighboring islands */
                set<int> components;
                
                //Traverse on all its neighbors
                for (int ind = 0; ind < 4; ind++) {
                    
                    // Coodinates of neigboring cell
                    int newRow = row + delRow[ind];
                    int newCol = col + delCol[ind];
                    
                    
                    if (isValid(newRow, newCol, n) && 
                        grid[newRow][newCol] == 1) {
                        
                        /* Perform union and store 
                        ultimate parent in the set */
                        int nodeNumber = newRow * n + newCol;
                        components.insert(ds.findUPar(nodeNumber));
                    }
                }
                
                // To store the size of current largest island
                int sizeTotal = 0;
                
                // Iterate on all the neighborinh ultimate parents
                for (auto it : components) {
                    
                    // Update the size
                    sizeTotal += ds.size[it];
                }
                
                // Store the maximum size of island
                ans = max(ans, sizeTotal + 1);
            }
        }
        
        // Edge case
        for (int cellNo = 0; cellNo < n * n; cellNo++) {
            
            // Keep the answer updated
            ans = max(ans, ds.size[ds.findUPar(cellNo)]);
        }
        
        // Return the answer
        return ans;
    }
};


int main() {
    vector<vector<int>> grid = {
        {1,0},
        {0,1}
    };

    // Creating instance of Solution class
    Solution sol;
    
    /* Function call to get the 
    size of the largest island */
    int ans = sol.largestIsland(grid);
    
    // Output
    cout << "The size of the largest island is: " << ans;
    
    return 0;
}
import java.util.*;

class DisjointSet {
    /* To store the ranks, parents and 
    sizes of different set of vertices */
    int[] rank, parent, size;

    // Constructor
    DisjointSet(int n) {
        rank = new int[n + 1];
        parent = new int[n + 1];
        size = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }

    // Function to find ultimate parent
    int findUPar(int node) {
        if (node == parent[node])
            return node;
        return parent[node] = findUPar(parent[node]);
    }

    // Function to implement union by rank
    void unionByRank(int u, int v) {
        int ulp_u = findUPar(u);
        int ulp_v = findUPar(v);
        if (ulp_u == ulp_v) return;
        if (rank[ulp_u] < rank[ulp_v]) {
            parent[ulp_u] = ulp_v;
        }
        else if (rank[ulp_v] < rank[ulp_u]) {
            parent[ulp_v] = ulp_u;
        }
        else {
            parent[ulp_v] = ulp_u;
            rank[ulp_u]++;
        }
    }

    // Function to implement union by size
    void unionBySize(int u, int v) {
        int ulp_u = findUPar(u);
        int ulp_v = findUPar(v);
        if (ulp_u == ulp_v) return;
        if (size[ulp_u] < size[ulp_v]) {
            parent[ulp_u] = ulp_v;
            size[ulp_v] += size[ulp_u];
        }
        else {
            parent[ulp_v] = ulp_u;
            size[ulp_u] += size[ulp_v];
        }
    }
}

// Solution class
class Solution {
    // DelRow and delCol for neighbors
    private int[] delRow = {-1, 0, 1, 0};
    private int[] delCol = {0, 1, 0, -1};
    
    /* Helper function to check 
    if a pixel is within boundaries */
    private boolean isValid(int i, int j, int n) {
        // Return false if pixel is invalid
        if (i < 0 || i >= n) return false;
        if (j < 0 || j >= n) return false;
        
        // Return true if pixel is valid
        return true;
    }
    
    /* Function to add initial islands to 
    the disjoint set data structure */
    private void addInitialIslands(int[][] grid, 
                                   DisjointSet ds, int n) {
        // Traverse all the cells in the grid
        for (int row = 0; row < n; row++) {
            for (int col = 0; col < n; col++) {
                // If the cell is not land, skip
                if (grid[row][col] == 0) continue;
                
                // Traverse on all the neighbors
                for (int ind = 0; ind < 4; ind++) {
                    // Get the coordinates of neighbor
                    int newRow = row + delRow[ind];
                    int newCol = col + delCol[ind];
                    
                    // If the cell is valid and a land cell
                    if (isValid(newRow, newCol, n) && 
                        grid[newRow][newCol] == 1) {
                        // Get the number for node
                        int nodeNo = row * n + col;
                        // Get the number for neighbor
                        int adjNodeNo = newRow * n + newCol;
                        
                        /* Take union of both nodes as they
                        are part of the same island */
                        ds.unionBySize(nodeNo, adjNodeNo);
                    }
                }
            }
        }
    }
    
    // Function to get the size of the largest island
    public int largestIsland(int[][] grid) {
        // Dimensions of grid
        int n = grid.length;
        
        // Disjoint set data structure
        DisjointSet ds = new DisjointSet(n * n);
        
        /* Function call to add initial
        islands in the disjoint set */
        addInitialIslands(grid, ds, n);
        
        // To store the answer
        int ans = 0;
        
        // Traverse on the grid
        for (int row = 0; row < n; row++) {
            for (int col = 0; col < n; col++) {
                
                // If the cell is a land cell, skip
                if (grid[row][col] == 1) continue;
                
                /* Set to store the ultimate 
                parents of neighboring islands */
                Set<Integer> components = new HashSet<>();
                
                // Traverse on all its neighbors
                for (int ind = 0; ind < 4; ind++) {
                    // Coordinates of neighboring cell
                    int newRow = row + delRow[ind];
                    int newCol = col + delCol[ind];
                    
                    if (isValid(newRow, newCol, n) && 
                        grid[newRow][newCol] == 1) {
                            
                        /* Perform union and store 
                        ultimate parent in the set */
                        int nodeNumber = newRow * n + newCol;
                        components.add(ds.findUPar(nodeNumber));
                    }
                }
                
                // To store the size of current largest island
                int sizeTotal = 0;
                
                // Iterate on all the neighboring ultimate parents
                for (int parent : components) {
                    // Update the size
                    sizeTotal += ds.size[ds.findUPar(parent)];
                }
                
                // Store the maximum size of island
                ans = Math.max(ans, sizeTotal + 1);
            }
        }
        
        // Edge case
        for (int cellNo = 0; cellNo < n * n; cellNo++) {
            // Keep the answer updated
            ans = Math.max(ans, ds.size[ds.findUPar(cellNo)]);
        }
        
        // Return the answer
        return ans;
    }

    public static void main(String[] args) {
        int[][] grid = {
            {1, 0},
            {0, 1}
        };

        // Creating instance of Solution class
        Solution sol = new Solution();
        
        /* Function call to get the 
        size of the largest island */
        int ans = sol.largestIsland(grid);
        
        // Output
        System.out.println("The size of the largest island is: " + ans);
    }
}
class DisjointSet:
    # To store the ranks, parents and 
    # sizes of different set of vertices
    def __init__(self, n):
        self.rank = [0] * (n + 1)
        self.parent = [i for i in range(n + 1)]
        self.size = [1] * (n + 1)
    
    # Function to find ultimate parent
    def findUPar(self, node):
        if node == self.parent[node]:
            return node
        self.parent[node] = self.findUPar(self.parent[node])
        return self.parent[node]
    
    # Function to implement union by rank
    def unionByRank(self, u, v):
        ulp_u = self.findUPar(u)
        ulp_v = self.findUPar(v)
        if ulp_u == ulp_v:
            return
        if self.rank[ulp_u] < self.rank[ulp_v]:
            self.parent[ulp_u] = ulp_v
        elif self.rank[ulp_v] < self.rank[ulp_u]:
            self.parent[ulp_v] = ulp_u
        else:
            self.parent[ulp_v] = ulp_u
            self.rank[ulp_u] += 1
    
    # Function to implement union by size
    def unionBySize(self, u, v):
        ulp_u = self.findUPar(u)
        ulp_v = self.findUPar(v)
        if ulp_u == ulp_v:
            return
        if self.size[ulp_u] < self.size[ulp_v]:
            self.parent[ulp_u] = ulp_v
            self.size[ulp_v] += self.size[ulp_u]
        else:
            self.parent[ulp_v] = ulp_u
            self.size[ulp_u] += self.size[ulp_v]
    
    def getSize(self, node):
        return self.size[self.findUPar(node)]

# Solution class
class Solution:
    # DelRow and delCol for neighbors
    delRow = [-1, 0, 1, 0]
    delCol = [0, 1, 0, -1]
    
    # Helper function to check if a 
    # pixel is within boundaries
    def isValid(self, i, j, n):
        # Return false if pixel is invalid
        if i < 0 or i >= n:
            return False
        if j < 0 or j >= n:
            return False
        # Return true if pixel is valid
        return True
    
    # Function to add initial islands to the 
    # disjoint set data structure
    def addInitialIslands(self, grid, ds, n):
        # Traverse all the cells in the grid
        for row in range(n):
            for col in range(n):
                # If the cell is not land, skip
                if grid[row][col] == 0:
                    continue
                
                # Traverse on all the neighbors
                for ind in range(4):
                    # Get the coordinates of neighbor
                    newRow = row + self.delRow[ind]
                    newCol = col + self.delCol[ind]
                    
                    # If the cell is valid and a land cell
                    if (self.isValid(newRow, newCol, n) and 
                        grid[newRow][newCol] == 1):
                            
                        # Get the number for node
                        nodeNo = row * n + col
                        # Get the number for neighbor
                        adjNodeNo = newRow * n + newCol
                        
                        # Take union of both nodes as 
                        # they are part of the same island
                        ds.unionBySize(nodeNo, adjNodeNo)
    
    # Function to get the size of the largest island
    def largestIsland(self, grid):
        # Dimensions of grid
        n = len(grid)
        
        # Disjoint set data structure
        ds = DisjointSet(n * n)
        
        # Function call to add initial 
        # islands in the disjoint set
        self.addInitialIslands(grid, ds, n)
        
        # To store the answer
        ans = 0
        
        # Traverse on the grid
        for row in range(n):
            for col in range(n):
                # If the cell is a land cell, skip
                if grid[row][col] == 1:
                    continue
                
                # Set to store the ultimate 
                # parents of neighboring islands
                components = set()
                
                # Traverse on all its neighbors
                for ind in range(4):
                    # Coordinates of neighboring cell
                    newRow = row + self.delRow[ind]
                    newCol = col + self.delCol[ind]
                    
                    if (self.isValid(newRow, newCol, n) and 
                        grid[newRow][newCol] == 1):
                        # Perform union and store 
                        # ultimate parent in the set
                        nodeNumber = newRow * n + newCol
                        components.add(ds.findUPar(nodeNumber))
                
                # To store the size of current largest island
                sizeTotal = 0
                
                # Iterate on all the neighboring ultimate parents
                for parent in components:
                    # Update the size
                    sizeTotal += ds.getSize(parent)
                
                # Store the maximum size of island
                ans = max(ans, sizeTotal + 1)
        
        # Edge case
        for cellNo in range(n * n):
            # Keep the answer updated
            ans = max(ans, ds.getSize(cellNo))
        
        # Return the answer
        return ans

# Main function to test the Solution class
if __name__ == "__main__":
    grid = [
        [1, 0],
        [0, 1]
    ]

    # Creating instance of Solution class
    sol = Solution()
    
    # Function call to get the size of the largest island
    ans = sol.largestIsland(grid)
    
    # Output
    print("The size of the largest island is:", ans)
class DisjointSet {
    // Constructor
    constructor(n) {
        /* To store the ranks, parents and 
        sizes of different set of vertices */
        this.rank = new Array(n + 1).fill(0);
        this.parent = new Array(n + 1).fill(0).map((_, i) => i);
        this.size = new Array(n + 1).fill(1);
    }

    // Function to find ultimate parent
    findUPar(node) {
        if (node === this.parent[node])
            return node;
        this.parent[node] = this.findUPar(this.parent[node]);
        return this.parent[node];
    }

    // Function to implement union by rank
    unionByRank(u, v) {
        const ulp_u = this.findUPar(u);
        const ulp_v = this.findUPar(v);
        if (ulp_u === ulp_v) return;
        if (this.rank[ulp_u] < this.rank[ulp_v]) {
            this.parent[ulp_u] = ulp_v;
        } else if (this.rank[ulp_v] < this.rank[ulp_u]) {
            this.parent[ulp_v] = ulp_u;
        } else {
            this.parent[ulp_v] = ulp_u;
            this.rank[ulp_u]++;
        }
    }

    // Function to implement union by size
    unionBySize(u, v) {
        const ulp_u = this.findUPar(u);
        const ulp_v = this.findUPar(v);
        if (ulp_u === ulp_v) return;
        if (this.size[ulp_u] < this.size[ulp_v]) {
            this.parent[ulp_u] = ulp_v;
            this.size[ulp_v] += this.size[ulp_u];
        } else {
            this.parent[ulp_v] = ulp_u;
            this.size[ulp_u] += this.size[ulp_v];
        }
    }

    getSize(node) {
        return this.size[this.findUPar(node)];
    }
}

// Solution class
class Solution {
    // DelRow and delCol for neighbors
    constructor() {
        this.delRow = [-1, 0, 1, 0];
        this.delCol = [0, 1, 0, -1];
    }

    // Helper function to check if a pixel is within boundaries
    isValid(i, j, n) {
        // Return false if pixel is invalid
        if (i < 0 || i >= n) return false;
        if (j < 0 || j >= n) return false;
        // Return true if pixel is valid
        return true;
    }

    /* Function to add initial islands to 
    the disjoint set data structure */
    addInitialIslands(grid, ds, n) {
        // Traverse all the cells in the grid
        for (let row = 0; row < n; row++) {
            for (let col = 0; col < n; col++) {
                // If the cell is not land, skip
                if (grid[row][col] === 0) continue;

                // Traverse on all the neighbors
                for (let ind = 0; ind < 4; ind++) {
                    // Get the coordinates of neighbor
                    const newRow = row + this.delRow[ind];
                    const newCol = col + this.delCol[ind];

                    // If the cell is valid and a land cell
                    if (this.isValid(newRow, newCol, n) && grid[newRow][newCol] === 1) {
                        // Get the number for node
                        const nodeNo = row * n + col;
                        // Get the number for neighbor
                        const adjNodeNo = newRow * n + newCol;

                        /* Take union of both nodes as 
                        they are part of the same island */
                        ds.unionBySize(nodeNo, adjNodeNo);
                    }
                }
            }
        }
    }

    // Function to get the size of the largest island
    largestIsland(grid) {
        // Dimensions of grid
        const n = grid.length;

        // Disjoint set data structure
        const ds = new DisjointSet(n * n);

        // Function call to add initial islands in the disjoint set
        this.addInitialIslands(grid, ds, n);

        // To store the answer
        let ans = 0;

        // Traverse on the grid
        for (let row = 0; row < n; row++) {
            for (let col = 0; col < n; col++) {
                // If the cell is a land cell, skip
                if (grid[row][col] === 1) continue;

                /* Set to store the ultimate parents 
                of neighboring islands */
                const components = new Set();

                // Traverse on all its neighbors
                for (let ind = 0; ind < 4; ind++) {
                    // Coordinates of neighboring cell
                    const newRow = row + this.delRow[ind];
                    const newCol = col + this.delCol[ind];

                    if (this.isValid(newRow, newCol, n) && grid[newRow][newCol] === 1) {
                        
                        /* Perform union and store 
                        ultimate parent in the set */
                        const nodeNumber = newRow * n + newCol;
                        components.add(ds.findUPar(nodeNumber));
                    }
                }

                // To store the size of current largest island
                let sizeTotal = 0;

                // Iterate on all the neighboring ultimate parents
                for (const parent of components) {
                    // Update the size
                    sizeTotal += ds.getSize(parent);
                }

                // Store the maximum size of island
                ans = Math.max(ans, sizeTotal + 1);
            }
        }

        // Edge case
        for (let cellNo = 0; cellNo < n * n; cellNo++) {
            // Keep the answer updated
            ans = Math.max(ans, ds.getSize(cellNo));
        }

        // Return the answer
        return ans;
    }
}

// Main function to test the Solution class
(function main() {
    const grid = [
        [1, 0],
        [0, 1]
    ];

    // Creating instance of Solution class
    const sol = new Solution();

    // Function call to get the size of the largest island
    const ans = sol.largestIsland(grid);

    // Output
    console.log("The size of the largest island is: " + ans);
})();

Complexity Analysis:

Time Complexity: O(N²) Using nested loops, and within the loops, all the operations take constant time.

Space Complexity: O(N²) The Disjoint set storing N² nodes (cells) will take up 2*N² space due to parent and size arrays.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Understanding:

How to store cells as nodes in the Disjoint Set?

Edge Cases:

What if all the cells are 1 in the grid?

Approach:

Dry Run:

Solution:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code