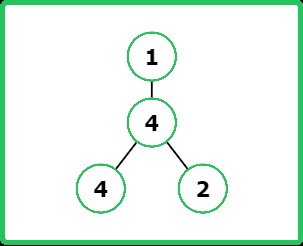
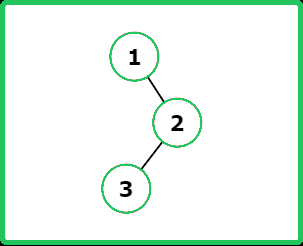
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
#include<bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int val) : data(val) , left(nullptr) , right(nullptr) {}
};
/**
* This method performs an inorder traversal of a binary tree
* using the Morris Traversal algorithm, which does not use
* additional space for a stack or recursion.
*/
class Solution {
public:
vector<int> getInorder(TreeNode* root) {
// Vector to store inorder traversal
vector<int> inorder;
// Pointer to current node
TreeNode* cur = root;
while (cur != nullptr) {
if (cur->left == nullptr) {
// Add current node's value and move to right child
inorder.push_back(cur->data);
cur = cur->right;
} else {
// Find predecessor
TreeNode* prev = cur->left;
while (prev->right && prev->right != cur) {
prev = prev->right;
}
/* Establish a temporary link and move to the
left child */
if (prev->right == nullptr) {
prev->right = cur;
cur = cur->left;
} else {
/* Remove the temporary link, add current node's value
and move to the right child */
prev->right = nullptr;
inorder.push_back(cur->data);
cur = cur->right;
}
}
}
// Return inorder traversal
return inorder;
}
};
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->left->right->right = new TreeNode(6);
Solution sol;
vector<int> inorder = sol.getInorder(root);
cout << "Binary Tree Morris Inorder Traversal: ";
for (int val : inorder) {
cout << val << " ";
}
cout << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
// Definition for a binary tree node.
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) { data = val; left = null; right = null; }
}
/**
* This method performs an inorder traversal of a binary tree
* using the Morris Traversal algorithm, which does not use
* additional space for a stack or recursion.
*/
class Solution {
public List<Integer> getInorder(TreeNode root) {
// List to store inorder traversal
List<Integer> inorder = new ArrayList<>();
// Pointer to the current node
TreeNode cur = root;
while (cur != null) {
if (cur.left == null) {
// Add current node's value and move to right child
inorder.add(cur.data);
cur = cur.right;
} else {
// Find the predecessor
TreeNode prev = cur.left;
while (prev.right != null && prev.right != cur) {
prev = prev.right;
}
/* Establish a temporary link and move to the
left child */
if (prev.right == null) {
prev.right = cur;
cur = cur.left;
} else {
/* Remove the temporary link, add current node's value
and move to the right child */
prev.right = null;
inorder.add(cur.data);
cur = cur.right;
}
}
}
// Return inorder traversal
return inorder;
}
}
// Example usage:
public class Main {
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(6);
Solution sol = new Solution();
List<Integer> inorder = sol.getInorder(root);
System.out.print("Binary Tree Morris Inorder Traversal: ");
for (int val : inorder) {
System.out.print(val + " ");
}
System.out.println();
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
# This method performs an inorder traversal of a binary tree
# using the Morris Traversal algorithm, which does not use
# additional space for a stack or recursion.
class Solution:
def getInorder(self, root):
# List to store inorder traversal
inorder = []
# Pointer to current node
cur = root
while cur is not None:
if cur.left is None:
# Add current node's value and move to right child
inorder.append(cur.data)
cur = cur.right
else:
# Find predecessor
prev = cur.left
while prev.right and prev.right != cur:
prev = prev.right
if prev.right is None:
# Establish temporary link
prev.right = cur
# Move to left child
cur = cur.left
else:
# Remove temporary link
# Add current node's value
# Move to right child
prev.right = None
inorder.append(cur.data)
cur = cur.right
# Return inorder traversal
return inorder
if __name__ == "__main__":
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.left.right.right = TreeNode(6)
sol = Solution()
inorder = sol.getInorder(root)
print("Binary Tree Morris Inorder Traversal:", end=" ")
for val in inorder:
print(val, end=" ")
print()
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null){
this.data = val;
this.left = left;
this.right = right;
}
}
/**
* This method performs an inorder traversal of a binary tree
* using the Morris Traversal algorithm, which does not use
* additional space for a stack or recursion.
*/
class Solution {
getInorder(root) {
// Array to store inorder traversal
let inorder = [];
// Pointer to current node
let cur = root;
while (cur !== null) {
if (cur.left === null) {
// Add current node's value and move to right child
inorder.push(cur.data);
cur = cur.right;
} else {
// Find the predecessor
let prev = cur.left;
while (prev.right !== null && prev.right !== cur) {
prev = prev.right;
}
/* Establish a temporary link and move to the
left child */
if (prev.right === null) {
prev.right = cur;
cur = cur.left;
} else {
/* Remove the temporary link, add current node's value
and move to the right child */
prev.right = null;
inorder.push(cur.data);
cur = cur.right;
}
}
}
// Return inorder traversal
return inorder;
}
}
// Example usage:
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(6);
let sol = new Solution();
let inorder = sol.getInorder(root);
console.log("Binary Tree Morris Inorder Traversal:", inorder.join(" "));