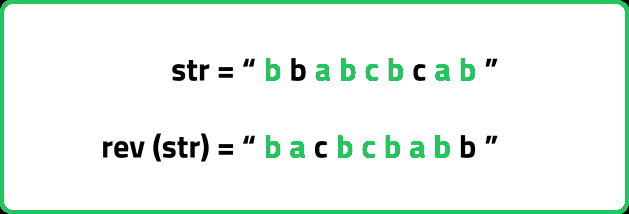Longest palindromic subsequence
Dynamic Programming
DP on strings
Hard
Given a string, Find the longest palindromic subsequence length in given string.
A palindrome is a sequence that reads the same backwards as forward.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
Examples:
Input: s = "eeeme"
Output: 4
Explanation: The longest palindromic subsequence is "eeee", which has a length of 4.
Input: s = "annb"
Output: 2
Explanation: The longest palindromic subsequence is "nn", which has a length of 2.
Input: s = "s"
Constraints
- 1 ≤ s.length ≤ 1000
Hints
- "Define dp[i][j] as the length of the longest palindromic subsequence in s[i:j]. Recurrence Relation: If s[i] == s[j]: dp[i][j]=dp[i+1][j−1]+2 Otherwise, remove one character and take the maximum LPS found: dp[i][j]=max(dp[i+1][j],dp[i][j−1])"
Company Tags
Bungie
Mastercard
Rakuten
Wayfair
Johnson & Johnson
Siemens Healthineers
Morgan Stanley
Roche
Dropbox
AMD
DoorDash
Unity Technologies
McKinsey & Company
Target
Boston Consulting Group
Pinterest
American Express
OYO Rooms
Square
Etsy
Activision Blizzard
Cerner
ARM
Salesforce
IBM
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe