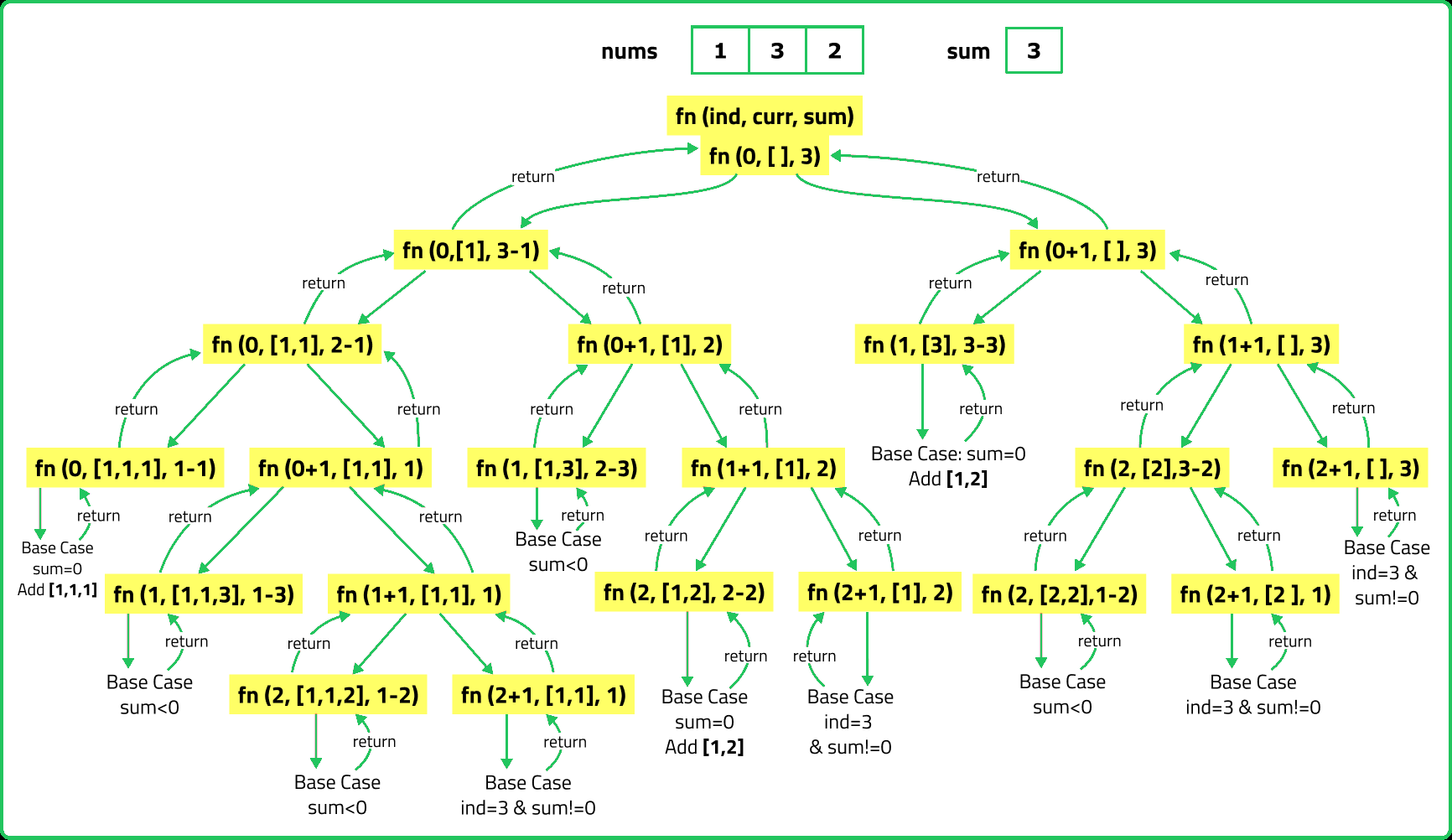
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Recursive function to find all subsequences with the given target sum
void func(vector<int>& v, int i, int sum, vector<int>& v2, vector<vector<int>>& ans) {
// Base case: if the sum is zero, add the current subsequence to the result
if (sum == 0) {
ans.push_back(v2);
return;
}
// Base case: if the sum becomes negative
if (sum < 0) {
return;
}
// Base case: if no elements are left
if (i < 0) {
return;
}
// Exclude the current element and move to the next
func(v, i - 1, sum, v2, ans);
// Include the current element in the subsequence
v2.push_back(v[i]);
// Recursively call the function with the included element
func(v, i, sum - v[i], v2, ans);
// Backtrack by removing the last added element
v2.pop_back();
}
// Main function to find all unique combinations of candidates that sum to the target
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> v;
// Start the recursive process
func(candidates, candidates.size() - 1, target, v, ans);
return ans;
}
};
// Main function to test the solution
int main() {
Solution sol;
vector<int> candidates = {2, 3, 6, 7};
int target = 7;
vector<vector<int>> result = sol.combinationSum(candidates, target);
for (const auto& combination : result) {
for (int num : combination) {
cout << num << " ";
}
cout << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
import java.util.ArrayList;
import java.util.List;
class Solution {
// Recursive function to find all subsequences with the given target sum
public void func(List<Integer> v, int i, int sum, List<Integer> v2, List<List<Integer>> ans) {
// Base case: if the sum is zero, add the current subsequence to the result
if (sum == 0) {
ans.add(new ArrayList<>(v2));
return;
}
// Base case: if the sum becomes negative or no elements are left
if (sum < 0 || i < 0) {
return;
}
// Exclude the current element and move to the next
func(v, i - 1, sum, v2, ans);
// Include the current element in the subsequence
v2.add(v.get(i));
// Recursively call the function with the included element
func(v, i, sum - v.get(i), v2, ans);
// Backtrack by removing the last added element
v2.remove(v2.size() - 1);
}
// Main function to find all unique combinations of candidates that sum to the target
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> v = new ArrayList<>();
// Convert the array to a list for easier manipulation
for (int num : candidates) {
v.add(num);
}
// Start the recursive process
func(v, v.size() - 1, target, new ArrayList<>(), ans);
return ans;
}
// Main method to test the solution
public static void main(String[] args) {
Solution sol = new Solution();
int[] candidates = {2, 3, 6, 7};
int target = 7;
List<List<Integer>> result = sol.combinationSum(candidates, target);
System.out.println(result);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution:
# Recursive function to find all subsequences with the given target sum
def func(self, v, i, sum, v2, ans):
# Base case: if the sum is zero, add the current subsequence to the result
if sum == 0:
ans.append(v2[:])
return
# Base case: if the sum becomes negative or no elements are left
if sum < 0 or i < 0:
return
# Exclude the current element and move to the next
self.func(v, i - 1, sum, v2, ans)
# Include the current element in the subsequence
v2.append(v[i])
# Recursively call the function with the included element
self.func(v, i, sum - v[i], v2, ans)
# Backtrack by removing the last added element
v2.pop()
# Main function to find all unique combinations of candidates that sum to the target
def combinationSum(self, candidates, target):
ans = []
# Create a copy of the candidates list for easier manipulation
v = candidates[:]
# Start the recursive process
self.func(v, len(v) - 1, target, [], ans)
return ans
# Main block to test the solution
if __name__ == "__main__":
sol = Solution()
candidates = [2, 3, 6, 7]
target = 7
result = sol.combinationSum(candidates, target)
print(result)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
class Solution {
// Recursive function to find all subsequences with the given target sum
func(v, i, sum, v2, ans) {
// Base case: if the sum is zero, add the current subsequence to the result
if (sum === 0) {
ans.push([...v2]);
return;
}
// Base case: if the sum becomes negative or no elements are left
if (sum < 0 || i < 0) {
return;
}
// Exclude the current element and move to the next
this.func(v, i - 1, sum, v2, ans);
// Include the current element in the subsequence
v2.push(v[i]);
// Recursively call the function with the included element
this.func(v, i, sum - v[i], v2, ans);
// Backtrack by removing the last added element
v2.pop();
}
// Main function to find all unique combinations of candidates that sum to the target
combinationSum(candidates, target) {
const ans = [];
const v2 = [];
// Start the recursive process
this.func(candidates, candidates.length - 1, target, v2, ans);
return ans;
}
}
// Main block to test the solution
const sol = new Solution();
const candidates = [2, 3, 6, 7];
const target = 7;
const result = sol.combinationSum(candidates, target);
console.log(result);