Burst balloons
- This problem, dubbed as the "Burst Balloons" problem, embodies the concept of dynamic programming, an essential technique widely used in software industry to solve optimization problems
- Its real-world application can be seen in resource allocation tasks where we need to make a sequence of interrelated decisions
- For example, in network routing, a form of this problem could be used to determine the optimal path (balloons to burst) that would minimize cost (maximize coins) while transferring data from source to destination
- It stands as a classic example showcasing the importance of decision optimization and state transition in programming
Given n balloons, indexed from 0 to n - 1, each balloon is painted with a number on it represented by an array nums. Burst all the balloons.
If the ith balloon is burst, the coins obtained are nums[i - 1] * nums[i] * nums[i + 1]. If i - 1 or i + 1 goes out of bounds of the array, treat it as if there is a balloon with a 1 painted on it.
Return the maximum coins that can be collected by bursting the balloons wisely.
Examples:
Input : nums = [3, 1, 5, 8]
Output : 167
Explanation :
nums = [3, 1, 5, 8] --> [3, 5, 8] --> [3, 8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167.
Input : nums = [1, 2, 3, 4]
Output : 40
Explanation :
nums = [1, 2, 3, 4] --> [1, 2, 4] --> [1, 4] --> [4] --> []
coins = 2*3*4 + 1*2*4 + 1*1*4 + 1*4*1 = 40.
Input : nums = [1, 5]
Constraints
- 1 <= n <= 300
- 1 <= nums[i] <= 100
Hints
- Define dp[i][j] as the maximum coins obtained by bursting balloons in the range [i, j].
- "The final burst at k contributes nums[i-1] * nums[k] * nums[j+1] coins. Solve subproblems first, then use them to compute dp[i][j]."
Company Tags
Editorial
Understanding:
From the question, we can easily understand that we must burst the balloons in a particular order to collect the maximum number of coins. For example, in the first case, we followed the order: 1, 5, 3, 8 to collect the maximum number of coins i.e. 167. So, the order of bursting the balloons will change the number of coins we can collect. There may be several orders that we can follow.
So, in order to find a valid order, can figure out the first balloon we will burst. Apparently, the entire array(i.e. given) is the range of the elements(i.e. the balloons) and anyone among the elements can be the first.
First, we will try to solve the problem using the technique we have learned in MCM. In the MCM, we selected the matrices sequentially so that the number of scalar multiplication is minimized. Similarly, here we can maintain an order where we will first try to choose the first element, then we can try to find the second one, and so on.
Now, let’s understand if we can really solve the problem using the above approach. Let’s consider the following example:
We are given an array: {b1, b2, b3, b4, b5, b6}. Each element of the given array is representing a balloon. Now, if we burst the b4, we will get a total of (b3*b4*b5) coins. After bursting b4, we are left with the left sub-problem {b1, b2, b3} and the right sub-problem {b5, b6} to solve.
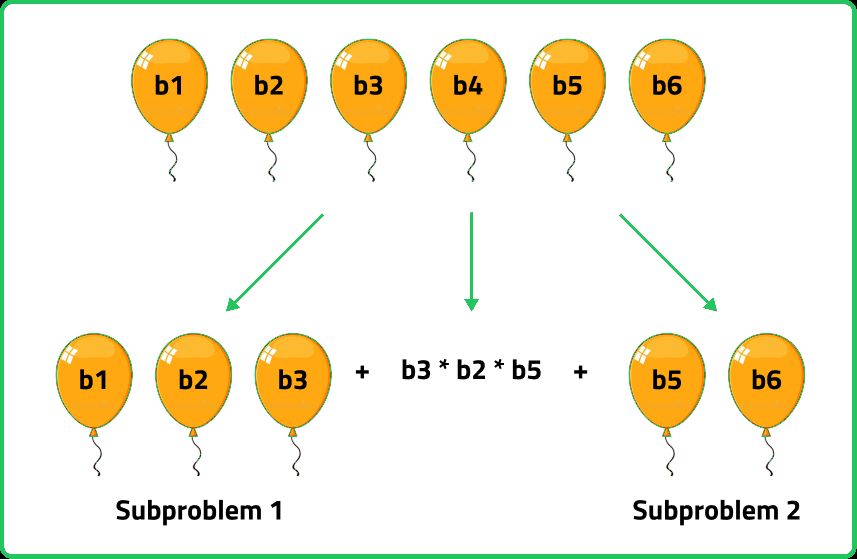Now, the question is, if we can say that the final answer will be the summation of the current number of coins and the answers from the left and right subproblems. The answer is No.
Let’s understand the reason behind this. Imagine, at first we burst the balloon b4. Then, we are left with the array: {b1, b2, b3, b5, b6}. Now, if we try to burst b3, it will be dependent on b5. Similarly, if we try to burst b5, it will be dependent on b3. Similarly, we can observe the same dependency in the case of other elements as well. So, we cannot solve the subproblems {b1, b2, b3} and {b4, b5} independently as they are dependent on each other.
Intuition:
Until now, we have clearly understood that we cannot solve this problem using this approach. So, we will just try to think in the opposite way. First, we tried to find out a balloon that we will burst first. But now, we will first try to find that balloon which we will burst last.
Note: The intuition is to first find the last balloon, then the second last, and so on. This is the sequence we need to follow to solve this problem. Now, let’s understand how the subproblems are independent in this approach:
Let’s consider the following example:
We are given an array: {b1, b2, b3, b4, b5, b6}. Assume, b4 be the last balloon we will burst. Then we can surely say, the total no. of coins we can get by bursting the balloon b4 is (1*b4*1). Now, we get two subproblems as usual: {b1, b2, b3} and {b5, b6}, and while choosing the second last balloon, we can ensure that b4 exists while bursting the second last balloon. If the second last balloon belongs to the 1st sub-problem i.e. {b1, b2, b3}, it will be only dependent on the last balloon i.e. b4 as the rightmost element will be b4. Similarly, if the second last balloon belongs to the 2nd sub-problem i.e. {b5, b6}, it will also be dependent only on the last balloon i.e. b4 as the leftmost element will be b4. The following illustration will clarify the concept:
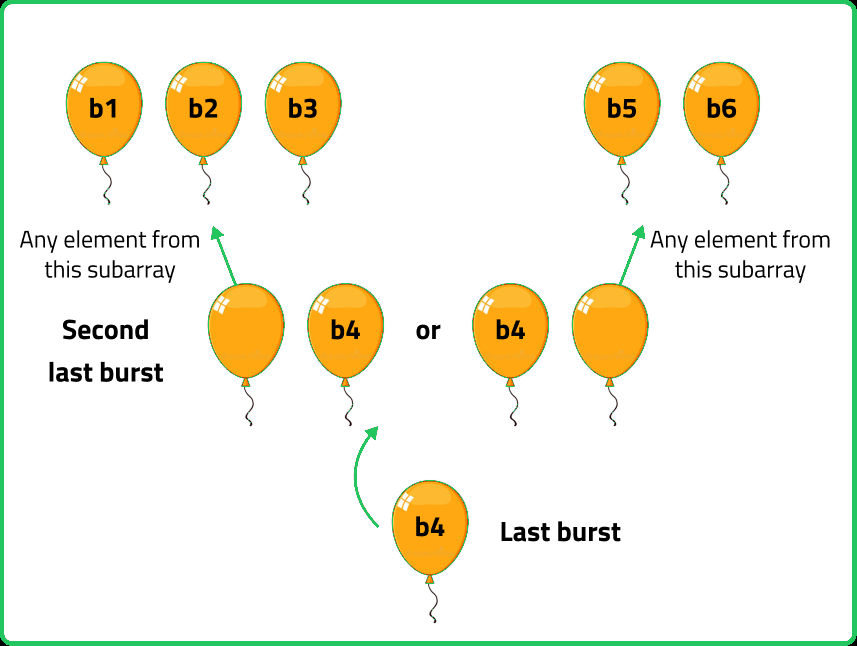
Now, we can clearly observe the subproblems are no anymore dependent on each other.
Rules to solve a problem on partition dp:
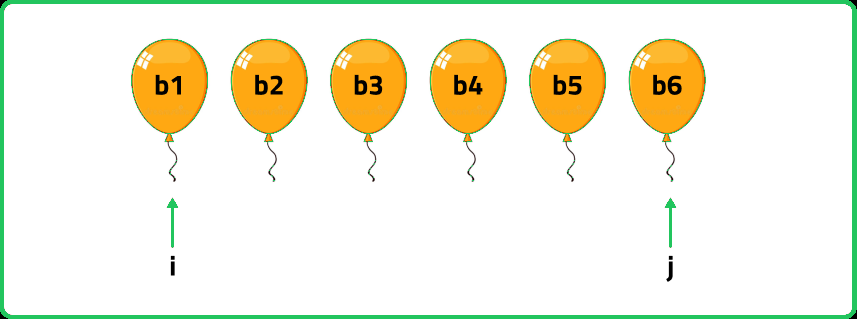
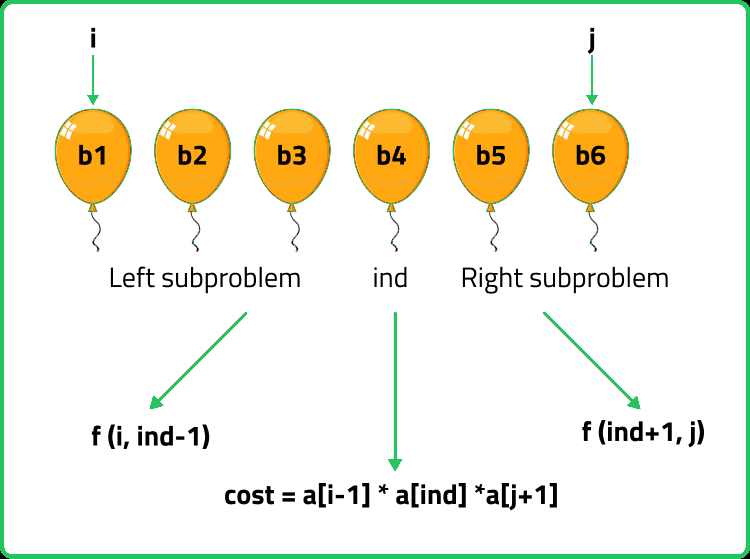
- Marking the array with i, j: We are given an array of balloons of size N. The entire array basically represents the range of the balloons. So, we will place i and j at both ends of the array. Here f(i, ind-1) is the left sub-problem, and f(ind+1, j) is the right sub-problem.
- Try all partitions: As we have figured out the logic for marking the i, and j pointers, we will move to the partitioning loop. We can simply write a for loop(say ind) starting from i to j, The problem is being broken in the following manner:
- Base Case: We can say that when i > j this is not a valid partition and so we will return 0.
- Return the best possible answer: Here, in this problem, we are trying to achieve the maximum possible answer i.e. the maximum number of coins. So, among all the costs calculated, we will just store the maximum one. And finally, the maximum cost will be our answer.
/*It is a pseudocode and it not tied to
any specific programming language*/
f(i, j){
//Partition loop
for(int ind = i; ind <= j; ind++){
cost = a[ind]*a[i-1]*a[j+1] + f(i, ind-1) + f(ind+1, j)
}
}/*It is a pseudocode and it not tied to
any specific programming language*/
f(i, j){
maxi = INT_MIN
for(int ind = i; ind <= j; ind++){
cost = a[ind]*a[i-1]*a[j+1] + f(i, ind-1) + f(ind+1, j)
maxi = max(cost, maxi)
}
}The recursive algorithm steps are as follows:
- Append 1 to both ends of the given array.
- Convert the problem to a recursive function marked by two pointers i and j.
- Use a loop to check all possible combinations of balloons and get all possible total numbers of coins.
- Return the maximum number of coins we can get.
- Base case: If i > j, we will return 0.
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Recursive function to calculate
the maximum coins obtained*/
int func(int i, int j, vector<int> &nums) {
if (i > j) return 0;
int maxCoins = INT_MIN;
// Iterate through each balloon to burst last
for (int k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
int coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
int remainingCoins = func(i, k - 1, nums) + func(k + 1, j, nums);
// Update the maximum coins
maxCoins = max(maxCoins, coins + remainingCoins);
}
//Return the result
return maxCoins;
}
public:
// Function to calculate the maximum coins obtained
int maxCoins(vector<int> &nums) {
int n = nums.size();
// Add 1 to the beginning and end of nums array
nums.insert(nums.begin(), 1);
nums.push_back(1);
// Call the helper function to compute maximum coins
return func(1, n, nums);
}
};
int main() {
vector<int> nums = {3, 1, 5, 8};
//Create an instance of Solution class
Solution sol;
cout << "Maximum coins obtained: " << sol.maxCoins(nums);
return 0;
}
import java.util.*;
class Solution {
/* Recursive function to calculate
the maximum coins obtained*/
private int func(int i, int j, int[] nums) {
if (i > j) return 0;
int maxCoins = Integer.MIN_VALUE;
// Iterate through each balloon to burst last
for (int k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
int coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
int remainingCoins = func(i, k - 1, nums) + func(k + 1, j, nums);
// Update the maximum coins
maxCoins = Math.max(maxCoins, coins + remainingCoins);
}
// Return the result
return maxCoins;
}
// Function to calculate the maximum coins obtained
public int maxCoins(int[] nums) {
int n = nums.length;
// Add 1 to the beginning and end of nums array
int[] newNums = new int[n + 2];
newNums[0] = 1;
newNums[n + 1] = 1;
System.arraycopy(nums, 0, newNums, 1, n);
// Call the helper function to compute maximum coins
return func(1, n, newNums);
}
public static void main(String[] args) {
int[] nums = {3, 1, 5, 8};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Maximum coins obtained: " + sol.maxCoins(nums));
}
}
class Solution:
""" Recursive function to calculate
the maximum coins obtained"""
def func(self, i, j, nums):
if i > j:
return 0
maxCoins = float('-inf')
# Iterate through each balloon to burst last
for k in range(i, j + 1):
""" Calculate the coins obtained
by bursting the k-th balloon last"""
coins = nums[i - 1] * nums[k] * nums[j + 1]
""" Recursively calculate the maximum
coins for the remaining balloons"""
remainingCoins = self.func(i, k - 1, nums) + self.func(k + 1, j, nums)
# Update the maximum coins
maxCoins = max(maxCoins, coins + remainingCoins)
# Return the result
return maxCoins
# Function to calculate the maximum coins obtained
def maxCoins(self, nums):
n = len(nums)
# Add 1 to the beginning and end of nums array
nums = [1] + nums + [1]
# Call the helper function to compute maximum coins
return self.func(1, n, nums)
if __name__ == "__main__":
nums = [3, 1, 5, 8]
# Create an instance of Solution class
sol = Solution()
print("Maximum coins obtained:", sol.maxCoins(nums))
class Solution {
/* Recursive function to calculate
the maximum coins obtained*/
func(i, j, nums) {
if (i > j) return 0;
let maxCoins = Number.MIN_VALUE;
// Iterate through each balloon to burst last
for (let k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
let coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
let remainingCoins = this.func(i, k - 1, nums) + this.func(k + 1, j, nums);
// Update the maximum coins
maxCoins = Math.max(maxCoins, coins + remainingCoins);
}
// Return the result
return maxCoins;
}
// Function to calculate the maximum coins obtained
maxCoins(nums) {
let n = nums.length;
// Add 1 to the beginning and end of nums array
nums = [1, ...nums, 1];
// Call the helper function to compute maximum coins
return this.func(1, n, nums);
}
}
const nums = [3, 1, 5, 8];
// Create an instance of Solution class
const sol = new Solution();
console.log("Maximum coins obtained:", sol.maxCoins(nums));
Complexity Analysis:
Time Complexity: Exponential.Space Complexity: O(N), As we are using auxiliary stack space of O(N).
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
In order to convert a recursive solution to memoization the following steps will be taken:- Declare a dp array of size [n+1][n+1]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The value of 'i' and 'j' ranges from 1 to n+1. Therefore, we need 2D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Recursive function to calculate
the maximum coins obtained*/
int func(int i, int j, vector<int> &nums, vector<vector<int>> &dp) {
if (i > j) return 0;
//Check if the subproblem is already solved
if (dp[i][j] != -1) return dp[i][j];
int maxCoins = INT_MIN;
// Iterate through each balloon to burst last
for (int k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
int coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
int remainingCoins = func(i, k - 1, nums, dp) + func(k + 1, j, nums, dp);
// Update the maximum coins
maxCoins = max(maxCoins, coins + remainingCoins);
}
//Return the result
return dp[i][j] = maxCoins;
}
public:
// Function to calculate the maximum coins obtained
int maxCoins(vector<int> &nums) {
int n = nums.size();
// Add 1 to the beginning and end of nums array
nums.insert(nums.begin(), 1);
nums.push_back(1);
// Create a DP array for memoization
vector<vector<int>> dp(n + 2, vector<int>(n + 2, -1));
// Call the helper function to compute maximum coins
return func(1, n, nums, dp);
}
};
int main() {
vector<int> nums = {3, 1, 5, 8};
//Create an instance of Solution class
Solution sol;
cout << "Maximum coins obtained: " << sol.maxCoins(nums);
return 0;
}
import java.util.*;
class Solution {
/* Recursive function to calculate
the maximum coins obtained*/
private int func(int i, int j, int[] nums, int[][] dp) {
if (i > j) return 0;
// Check if the subproblem is already solved
if (dp[i][j] != -1) return dp[i][j];
int maxCoins = Integer.MIN_VALUE;
// Iterate through each balloon to burst last
for (int k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
int coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
int remainingCoins = func(i, k - 1, nums, dp) + func(k + 1, j, nums, dp);
// Update the maximum coins
maxCoins = Math.max(maxCoins, coins + remainingCoins);
}
// Return the result
return dp[i][j] = maxCoins;
}
// Function to calculate the maximum coins obtained
public int maxCoins(int[] nums) {
int n = nums.length;
// Add 1 to the beginning and end of nums array
int[] newNums = new int[n + 2];
newNums[0] = 1;
newNums[n + 1] = 1;
System.arraycopy(nums, 0, newNums, 1, n);
// Create a DP array for memoization
int[][] dp = new int[n + 2][n + 2];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
// Call helper function to compute maximum coins
return func(1, n, newNums, dp);
}
public static void main(String[] args) {
int[] nums = {3, 1, 5, 8};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Maximum coins obtained: " + sol.maxCoins(nums));
}
}
class Solution:
""" Recursive function to calculate
the maximum coins obtained"""
def func(self, i, j, nums, dp):
if i > j:
return 0
# Check if the subproblem is already solved
if dp[i][j] != -1:
return dp[i][j]
maxCoins = float('-inf')
# Iterate through each balloon to burst last
for k in range(i, j + 1):
""" Calculate the coins obtained by
bursting the k-th balloon last"""
coins = nums[i - 1] * nums[k] * nums[j + 1]
""" Recursively calculate the maximum
coins for the remaining balloons"""
remainingCoins = self.func(i, k - 1, nums, dp) + self.func(k + 1, j, nums, dp)
# Update the maximum coins
maxCoins = max(maxCoins, coins + remainingCoins)
# Return the result
dp[i][j] = maxCoins
return maxCoins
# Function to calculate the maximum coins obtained
def maxCoins(self, nums):
n = len(nums)
# Add 1 to the beginning and end of nums array
nums = [1] + nums + [1]
# Create a DP array for memoization
dp = [[-1] * (n + 2) for _ in range(n + 2)]
# Call the helper function to compute maximum coins
return self.func(1, n, nums, dp)
if __name__ == "__main__":
nums = [3, 1, 5, 8]
# Create an instance of Solution class
sol = Solution()
print("Maximum coins obtained:", sol.maxCoins(nums))
class Solution {
/* Recursive function to calculate
the maximum coins obtained*/
func(i, j, nums, dp) {
if (i > j) return 0;
// Check if the subproblem is already solved
if (dp[i][j] !== -1) return dp[i][j];
let maxCoins = Number.MIN_VALUE;
// Iterate through each balloon to burst last
for (let k = i; k <= j; k++) {
/* Calculate the coins obtained
by bursting the k-th balloon last*/
let coins = nums[i - 1] * nums[k] * nums[j + 1];
/* Recursively calculate the maximum
coins for the remaining balloons*/
let remainingCoins = this.func(i, k - 1, nums, dp) + this.func(k + 1, j, nums, dp);
// Update the maximum coins
maxCoins = Math.max(maxCoins, coins + remainingCoins);
}
// Return the result
dp[i][j] = maxCoins;
return dp[i][j];
}
// Function to calculate the maximum coins obtained
maxCoins(nums) {
let n = nums.length;
// Add 1 to the beginning and end of nums array
nums = [1, ...nums, 1];
// Create a DP array for memoization
let dp = Array.from({ length: n + 2 }, () => Array(n + 2).fill(-1));
// Call the helper function to compute maximum coins
return this.func(1, n, nums, dp);
}
}
const nums = [3, 1, 5, 8];
// Create an instance of Solution class
const sol = new Solution();
console.log("Maximum coins obtained:", sol.maxCoins(nums));
Complexity Analysis:
Time Complexity: O(N3), There are total N2 no. of states. And for each state, we are running a partitioning loop roughly for N times.Space Complexity: O(N2) + Auxiliary stack space of O(N), N2 for the dp array we are using.
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n+2][n+2]: As the highest value of j can have is 'n' and in that case, it will search for the value arr[j+1] i.e. arr[n+1]. So, to handle this case, we need the size to be n+2.
- Handle the base case: We knew in the recursive code the base case was when i > j, it meant that there are no valid partition. So, to cover this case we can initialize the entire dp array with 0.
- Next, memoization is a top-down approach, whereas tabulation is bottom-up. Our changing parameters i and j will change in opposite directions, i.e i will change from n→1 and j will change from 1→ n.
- After that, copy down the recursive logic inside the nested loops to get the tabulation code.
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
// Function to calculate the maximum coins obtained
int maxCoins(vector<int> &nums) {
int n = nums.size();
// Add 1 to the beginning and end of nums array
nums.insert(nums.begin(), 1);
nums.push_back(1);
// Create a DP array for memoization
vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
if (i > j) continue;
int maxi = INT_MIN;
/* Iterate through each possible
balloon to burst last*/
for (int ind = i; ind <= j; ind++) {
/* Calculate the coins obtained by
bursting the ind-th balloon last*/
int coins = nums[i - 1] * nums[ind] * nums[j + 1];
/* Calculate the maximum coins
for the remaining balloons*/
int remainingCoins = dp[i][ind - 1] + dp[ind + 1][j];
// Update the maximum coins
maxi = max(maxi, coins + remainingCoins);
}
//Store the maximum value in dp table
dp[i][j] = maxi;
}
}
//Return the result
return dp[1][n];
}
};
int main() {
vector<int> nums = {3, 1, 5, 8};
//Create an instance of Solution class
Solution sol;
//Print the result
cout << "Maximum coins obtained: " << sol.maxCoins(nums) << "\n";
return 0;
}
import java.util.*;
class Solution {
// Function to calculate the maximum coins obtained
public int maxCoins(int[] nums) {
int n = nums.length;
// Add 1 to the beginning and end of nums array
int[] newNums = new int[n + 2];
newNums[0] = 1;
newNums[n + 1] = 1;
System.arraycopy(nums, 0, newNums, 1, n);
// Create a DP array for memoization
int[][] dp = new int[n + 2][n + 2];
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
if (i > j) continue;
int maxi = Integer.MIN_VALUE;
/* Iterate through each possible
balloon to burst last*/
for (int ind = i; ind <= j; ind++) {
/* Calculate the coins obtained by
bursting the ind-th balloon last*/
int coins = newNums[i - 1] * newNums[ind] * newNums[j + 1];
/* Calculate the maximum coins
for the remaining balloons*/
int remainingCoins = dp[i][ind - 1] + dp[ind + 1][j];
// Update the maximum coins
maxi = Math.max(maxi, coins + remainingCoins);
}
// Store the maximum value in dp table
dp[i][j] = maxi;
}
}
// Return the result
return dp[1][n];
}
public static void main(String[] args) {
int[] nums = {3, 1, 5, 8};
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("Maximum coins obtained: " + sol.maxCoins(nums));
}
}
class Solution:
# Function to calculate the maximum coins obtained
def maxCoins(self, nums):
n = len(nums)
# Add 1 to the beginning and end of nums array
nums = [1] + nums + [1]
# Create a DP array for memoization
dp = [[0] * (n + 2) for _ in range(n + 2)]
for i in range(n, 0, -1):
for j in range(1, n + 1):
if i > j:
continue
maxi = float('-inf')
""" Iterate through each possible
balloon to burst last"""
for ind in range(i, j + 1):
""" Calculate the coins obtained by
bursting the ind-th balloon last"""
coins = nums[i - 1] * nums[ind] * nums[j + 1]
# Calculate the maximum coins for the remaining balloons
remainingCoins = dp[i][ind - 1] + dp[ind + 1][j]
# Update the maximum coins
maxi = max(maxi, coins + remainingCoins)
# Store the maximum value in dp table
dp[i][j] = maxi
# Return the result
return dp[1][n]
if __name__ == "__main__":
nums = [3, 1, 5, 8]
# Create an instance of Solution class
sol = Solution()
# Print the result
print("Maximum coins obtained:", sol.maxCoins(nums))
class Solution {
// Function to calculate the maximum coins obtained
maxCoins(nums) {
let n = nums.length;
// Add 1 to the beginning and end of nums array
nums = [1, ...nums, 1];
// Create a DP array for memoization
let dp = Array.from({ length: n + 2 }, () => Array(n + 2).fill(0));
for (let i = n; i >= 1; i--) {
for (let j = 1; j <= n; j++) {
if (i > j) continue;
let maxi = Number.MIN_VALUE;
/* Iterate through each possible
balloon to burst last*/
for (let ind = i; ind <= j; ind++) {
/* Calculate the coins obtained by
bursting the ind-th balloon last*/
let coins = nums[i - 1] * nums[ind] * nums[j + 1];
// Calculate the maximum coins for the remaining balloons
let remainingCoins = dp[i][ind - 1] + dp[ind + 1][j];
// Update the maximum coins
maxi = Math.max(maxi, coins + remainingCoins);
}
// Store the maximum value in dp table
dp[i][j] = maxi;
}
}
// Return the result
return dp[1][n];
}
}
const nums = [3, 1, 5, 8];
// Create an instance of Solution class
const sol = new Solution();
// Print the result
console.log("Maximum coins obtained:", sol.maxCoins(nums));
Complexity Analysis:
Time Complexity:O(N3), There are total N2 no. of states. And for each state, we are running a partitioning loop roughly for N timesSpace Complexity:O(N2), N2 for the dp array we are using.
Frequently Occurring Doubts
Q: Why do we solve the problem in reverse (choosing the last balloon to burst)?
A: Bursting in order creates dependencies on future states. If we choose the last balloon to burst in a range, then only adjacent balloons remain, allowing clean DP transitions.
Q: Why do we add 1 at both ends of nums?
A: The out-of-bounds multipliers act as 1, simplifying boundary calculations.
Interview Followup Questions
Q: How would you reconstruct the actual order of bursting?
A: Maintain a parent[][] array to store which balloon was burst last in dp[i][j], then backtrack to extract the sequence.
Q: What if the order of bursting mattered (not choosing the last burst dynamically)?
A: This becomes a greedy scheduling problem, requiring a different strategy to decide the next balloon to burst.
Notes
Code
167
40
1053