Best time to buy and sell stock
Dynamic Programming
DP on stocks
Medium
- While this problem is a simplified version, the concept is used in the development of algorithmic trading software
- These software tools use complex algorithms, often based on this kind of problem, to automatically execute trades when certain conditions are met (like when it's most profitable to buy or sell a stock)
- High-frequency trading, a type of algorithmic trading that places a large number of trades very quickly, often relies on this type of decision-making logic
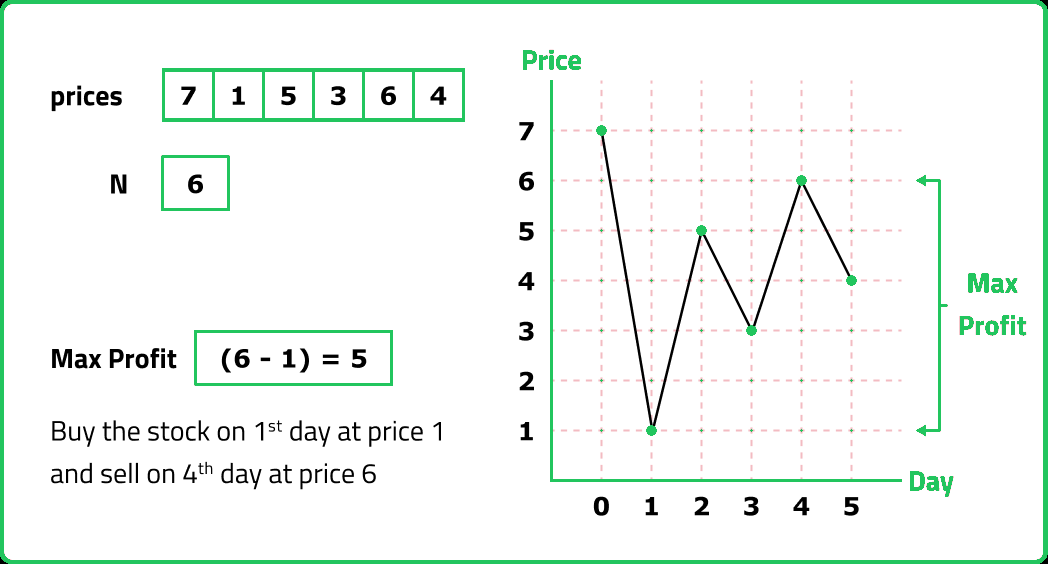
Given an array arr of n integers, where arr[i] represents price of the stock on the ith day. Determine the maximum profit achievable by buying and selling the stock at most once.
The stock should be purchased before selling it, and both actions cannot occur on the same day.
Examples:
Input: arr = [10, 7, 5, 8, 11, 9]
Output: 6
Explanation: Buy on day 3 (price = 5) and sell on day 5 (price = 11), profit = 11 - 5 = 6.
Input: arr = [5, 4, 3, 2, 1]
Output: 0
Explanation: In this case, no transactions are made. Therefore, the maximum profit remains 0.
Input: arr = [3, 8, 1, 4, 6, 2]
Constraints
- 1 <= n<= 105
- 0 <= arr[i] <= 106
Hints
- A naive brute-force approach would check all pairs (buy, sell), iterating over all possible purchase and sale days, resulting in an O(n²) time complexity.
- "A more optimal O(n) solution involves a single traversal with two variables: min_price: Tracks the lowest price seen so far. max_profit: Tracks the highest profit achievable at each step."
Company Tags
Walmart
Intel
AMD
Etsy
MongoDB
Boston Consulting Group
Zoho
Medtronic
ARM
Target
NVIDIA
Activision Blizzard
Qualcomm
IBM
Lyft
Electronic Arts
GE Healthcare
Salesforce
Reddit
PayPal
Twilio
Robinhood
Chewy
Snowflake
Alibaba
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe