Find peak element
Binary Search
FAQs
Hard
- This type of problem or its underlying concept is commonly utilized in Data Analysis and Financial sectors
- For example, in Stock Market Analysis, peak detection is critical in identifying patterns and trends, especially in time series data
- When visualizing stock prices, a "peak" would represent a maximum point (local maxima) before prices drop, or in other words, an optimal sell point
- Thus, efficient algorithms for identifying "peaks" from array-like data are crucial for decision-making processes in these areas
- This gives a real-world importance to such a seemingly theoretical problem
Given an array arr of integers. A peak element is defined as an element greater than both of its neighbors. Formally, if arr[i] is the peak element, arr[i - 1] < arr[i] and arr[i + 1] < arr[i]. Find the index(0-based) of a peak element in the array. If there are multiple peak numbers, return the index of any peak number.
Note: As there can be many peak values, 1 is given as output if the returned index is a peak number, otherwise 0.
Examples:
Input : arr = [1, 2, 3, 4, 5, 6, 7, 8, 5, 1]
Output: 7
Explanation: In this example, there is only 1 peak that is at index 7.
Input : arr = [1, 2, 1, 3, 5, 6, 4]
Output: 1
Explanation: In this example, there are 2 peak numbers at indices 1 and 5. We can consider any of them.
Input : arr = [-2, -1, 3, 4, 5]
Constraints
- 1 <= arr.length <= 1000
- -231 <= arr[i] <= 231 - 1
- arr[i] != arr[i + 1] for all valid i.
- For arr[0], its left element can be considered as -∞
- For arr[n-1], its right element can be considered as -∞
Hints
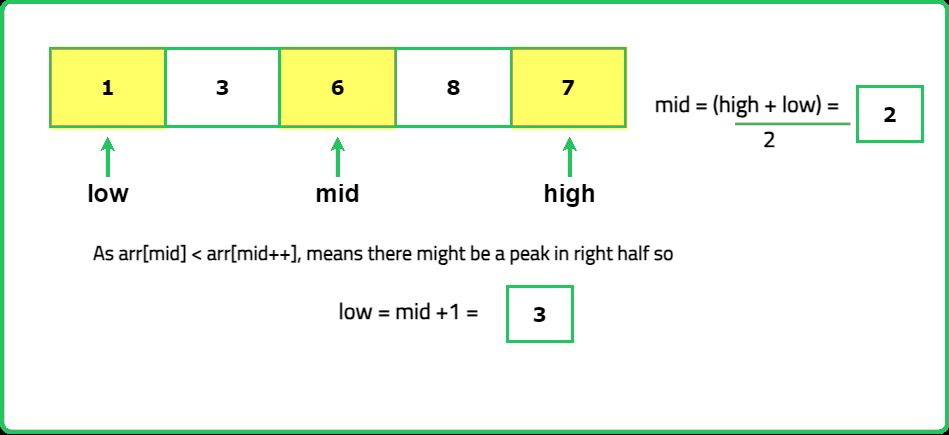
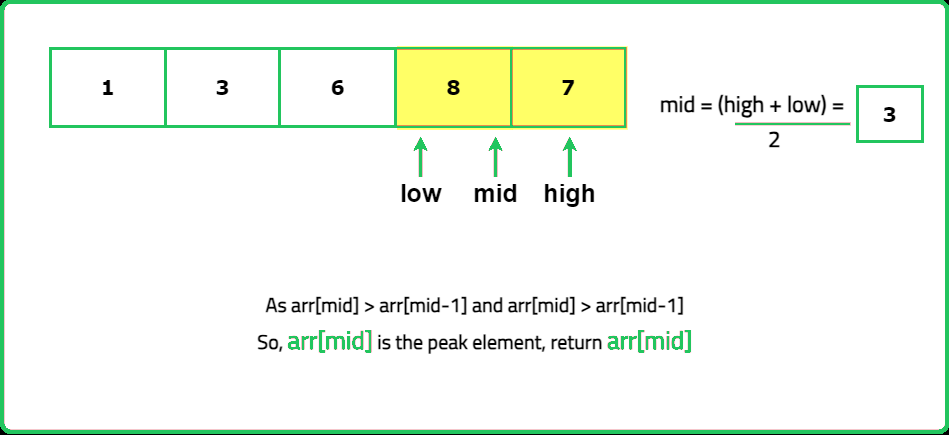
- You can find a peak in O(logn) using binary search
- "If an element is not a peak, at least one of its neighbors is greater. This ensures that moving toward the greater neighbor will lead to a peak. The problem guarantees at least one peak exists, so binary search always converges to a peak."
Company Tags
Epic Games
Dropbox
PwC
Square
Nutanix
Ubisoft
Alibaba
Philips Healthcare
Broadcom
Intel
Oracle
Chewy
Docker
Mastercard
IBM
Optum
Morgan Stanley
Epic Systems
Bloomberg
Seagate Technology
Roblox
Qualcomm
GE Healthcare
Airbnb
Flipkart
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe