Insertion Sorting
Sorting
Algorithms
Easy
- Insertion sort, the algorithm underlying this problem, is used extensively in computer programming not only for sorting arrays but also for organizing and retrieving data efficiently
- It is especially useful when dealing with small data sets or lists that are nearly sorted because it works faster in such cases
- Flash memory algorithms typically use this sorting method due to its stability and less requirement of write swaps
- Moreover, it's used in online sorting where the list is being actively updated while being maintained in sorted order
Given an array of integers called nums, sort the array in non-decreasing order using the insertion sort algorithm and return the sorted array.
A sorted array in non-decreasing order is an array where each element is greater than or equal to all preceding elements in the array.
Examples:
Input: nums = [7, 4, 1, 5, 3]
Output: [1, 3, 4, 5, 7]
Explanation: 1 <= 3 <= 4 <= 5 <= 7.
Thus the array is sorted in non-decreasing order.
Input: nums = [5, 4, 4, 1, 1]
Output: [1, 1, 4, 4, 5]
Explanation: 1 <= 1 <= 4 <= 4 <= 5.
Thus the array is sorted in non-decreasing order.
Input: nums = [3, 2, 3, 4, 5]
Constraints
- 1 <= nums.length <= 1000
- -104 <= nums[i] <= 104
- nums[i] may contain duplicate values.
Hints
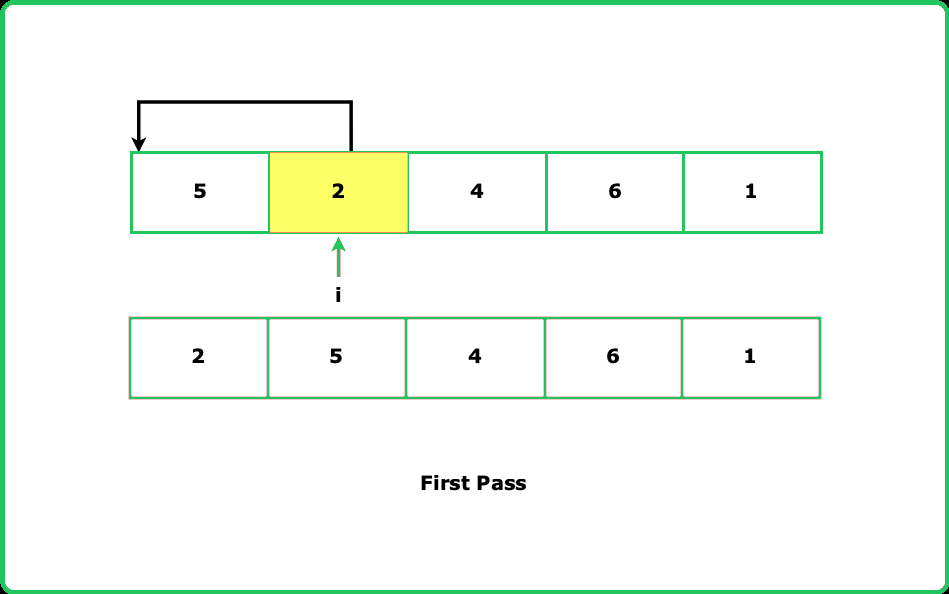
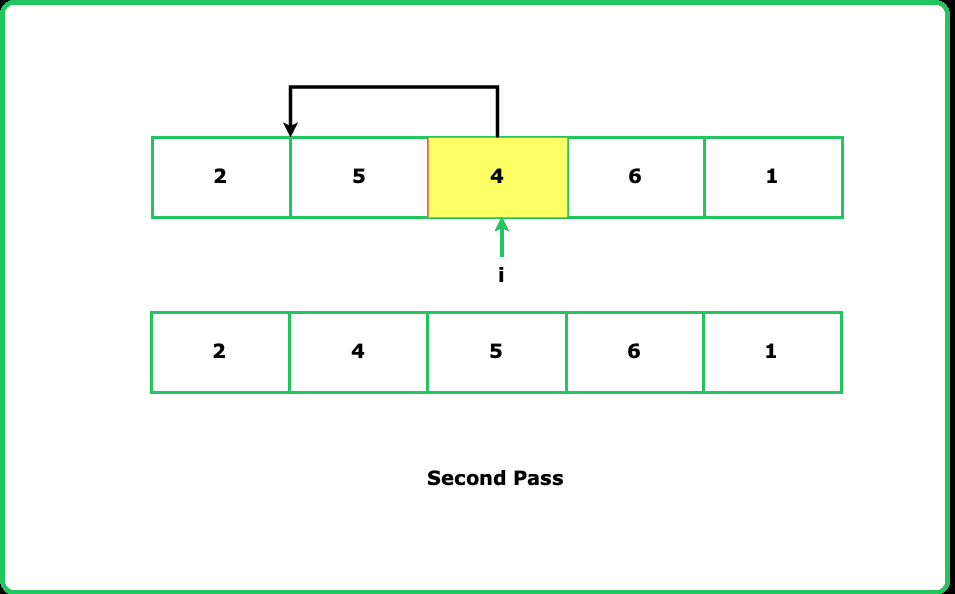
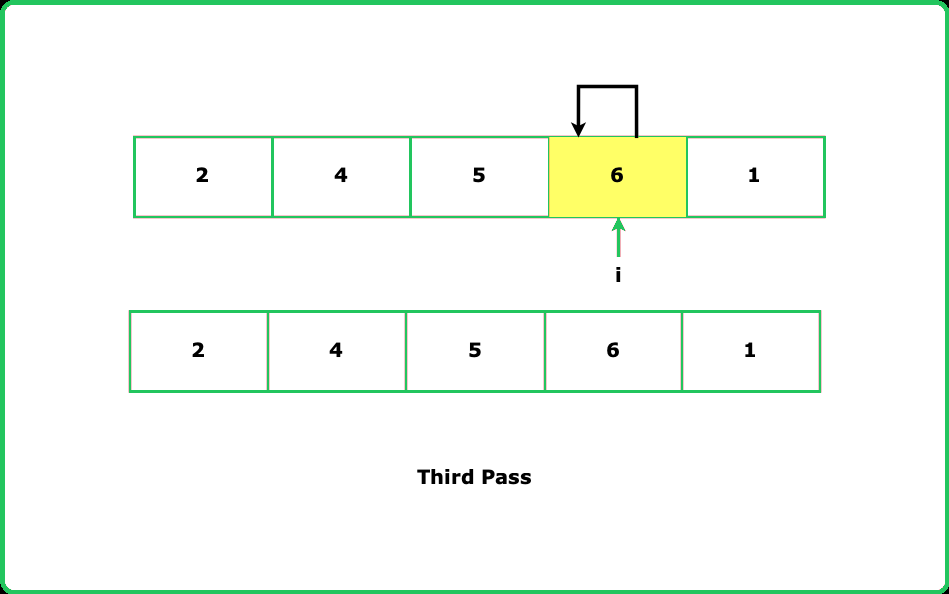
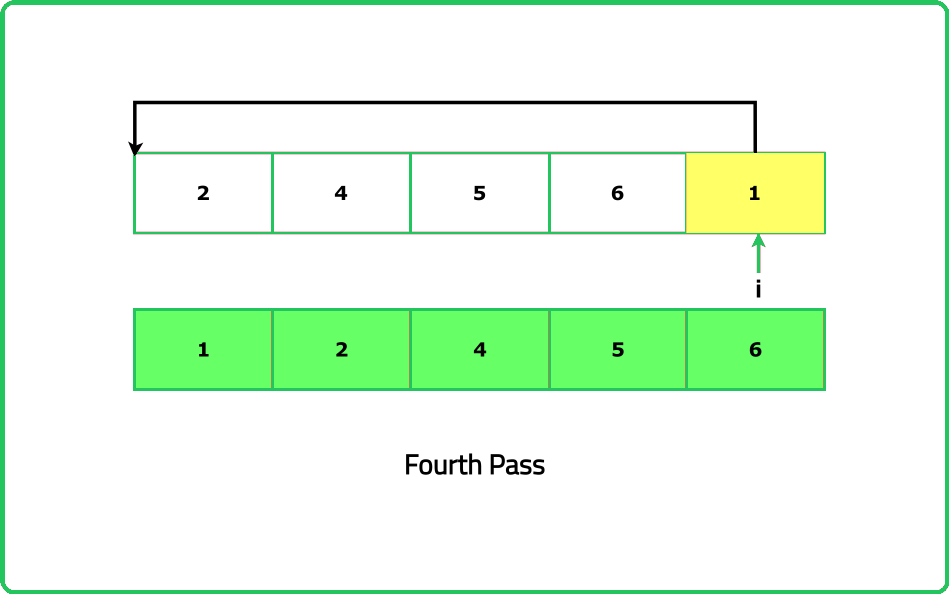
- Think of the array as divided into a sorted and unsorted portion. Start with the first element as "sorted" and expand this portion by inserting elements from the unsorted part.
- In cases where the key is already greater than or equal to the largest element in the sorted portion, no shifts are needed, improving efficiency for nearly sorted arrays.
Company Tags
Rakuten
Medtronic
PayPal
Optum
Pinterest
Oracle
Johnson & Johnson
Byju's
NVIDIA
JPMorgan Chase
Docker
Zoho
Shopify
Etsy
Alibaba
Roche
IBM
Snowflake
Salesforce
McKinsey & Company
Goldman Sachs
Mastercard
American Express
Cloudflare
Bain & Company
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro