Best time to buy and sell stock II

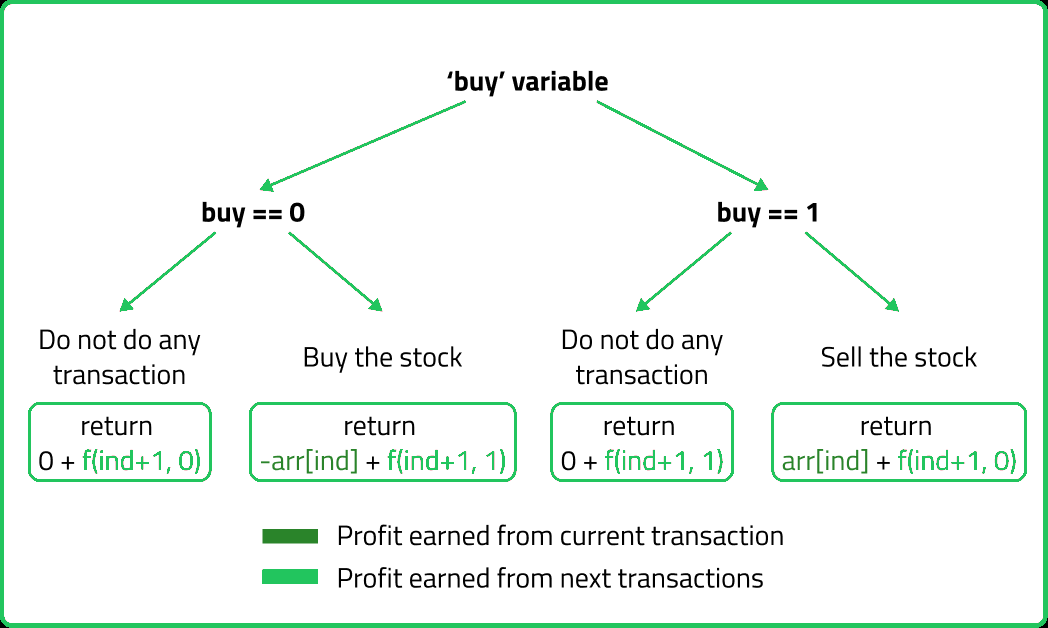
Upon observation we find that every day, there will be two choices, either to do nothing and move to the next day or to buy/sell (based on the last transaction) and find out the profit. Therefore we need to generate all the choices in order to compare the profit. As we need to try out all the possible choices, we will use recursion.

Steps to form the recursive solution:

Express the problem in terms of indexes: We need to consider the number of days, so one variable will be the array index (let's call it 'ind'). Additionally, we need to adhere to the condition that a stock cannot be bought again until it has been sold first. Therefore, a second variable 'buy' is needed to indicate whether the stock can be bought or sold on a particular day.

f(ind, buy) will give the maximum profit that can be generated from day 'ind' to day (n-1), where 'buy' tells that whether we need to buy or sell the stock at day 'ind'.

Try out all possible choices at a given index: Every day, there will be two choices, either to buy/sell the stock(based on the buy variable’s value) or to do nothing and move on to the next day. As we need to generate all the choices, use the pick/non-pick technique to the same.

Case 1: When buy == 0, the stock can be bought. If we can buy the stock on a particular day, there will be agian two options:

Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,0). As we have not bought the stock, the ‘buy’ variable value will still remain 0, indicating that we can buy the stock the next day.

Option 2: The other option is to buy the stock on the current day. In this case, the net profit earned from the current transaction will be -arr[i]. As we are buying the stock, it means we are giving money out of our pocket, therefore the profit earned is negative. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1). As we have bought the stock, the ‘buy’ variable value will change to 1, indicating that we can’t buy and only sell the stock the next day.

Case 2: When buy == 1, we can sell the stock. If we can sell the stock on a particular day, we will have two options:

Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1). As we have not bought the stock, the ‘buy’ variable value will still remain at 1, indicating that we can’t buy and only sell the stock the next day.

Option 2: The other option is to sell the stock on the current day. In this case, the net profit earned from the current transaction will be +arr[i]. As we are selling the stock, we are putting the money into our pocket, therefore the profit earned is positive. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1,0). As the stock has been sold, the ‘buy’ variable value will change to 0, indicating that we can buy the stock the next day.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy){
    //Base case
    if(buy == 0){
        op1 = 0 + f(ind + 1, 0)
        op2 = -arr[ind] + f(ind + 1, 1)
    }
    if(buy == 1){
        op1 = 0 + f(ind + 1, 1)
        op2 = arr[ind] + f(ind + 1, 0)
    }
           
}

Take the maximum of all choices: As we are looking to maximize the profit earned, return the maximum value in both cases.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy){
    //Base case
    if(buy == 0){
        op1 = 0 + f(ind + 1, 0)
        op2 = -arr[ind] + f(ind + 1, 1)
    }
    if(buy == 1){
        op1 = 0 + f(ind + 1, 1)
        op2 = arr[ind] + f(ind + 1, 0)
    }
    return max(op1, op2)    
}

Base cases: If ind == n, it means we have finished trading on all days, and there is no more money that we can get, therefore simply return 0.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find the maximum profit earned using recursion
    int func(int ind, int buy, int n, vector<int> &arr) {
        // Base case 
        if (ind == n) {
            return 0;
        }

        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = max(0 + func(ind + 1, 0, n, arr), (-1)*arr[ind] + func(ind + 1, 1, n, arr));
        }
        
        //We can sell the stock
        if (buy == 1) { 
            profit = max(0 + func(ind + 1, 1, n, arr), arr[ind] + func(ind + 1, 0, n, arr));
        }

        // Return the calculated profit
        return profit;
    }
public:
    //Function to calculate the maximum profit earned 
    int stockBuySell(vector<int> &arr, int n) {
        if (n == 0) 
            return 0;

        int ans = func(0, 0, n, arr);
        
        //Return the maximum profit
        return ans;
    }
};
int main() {
    int n = 6;
    vector<int> arr = {7, 1, 5, 3, 6, 4};
    
    //Create an instance of Solution class
    Solution sol;

    // Call the stockBuySell function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n);

    return 0;
}


import java.util.*;

class Solution {
    // Function to find the maximum profit earned using recursion
    private int func(int ind, int buy, int n, int[] arr) {
        // Base case 
        if (ind == n) {
            return 0;
        }

        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = Math.max(0 + func(ind + 1, 0, n, arr), (-1)*arr[ind] + func(ind + 1, 1, n, arr));
        }
        
        // We can sell the stock
        if (buy == 1) { 
            profit = Math.max(0 + func(ind + 1, 1, n, arr), arr[ind] + func(ind + 1, 0, n, arr));
        }

        // Return the calculated profit
        return profit;
    }

    // Function to calculate the maximum profit earned 
    public int stockBuySell(int[]arr, int n) {
        if (n == 0) 
            return 0;

        int ans = func(0, 0, n, arr);
        
        // Return the maximum profit
        return ans;
    }

    public static void main(String[] args) {
        int n = 6;
        int[] arr = {7, 1, 5, 3, 6, 4};
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n));
    }
}
class Solution:
    # Function to find the maximum profit earned using recursion
    def func(self, ind, buy, n, arr):
        # Base case 
        if ind == n:
            return 0

        profit = 0
        
        # We can buy the stock
        if buy == 0:
            profit = max(0 + self.func(ind + 1, 0, n, arr), (-1)*arr[ind] + self.func(ind + 1, 1, n, arr))
        
        # We can sell the stock
        if buy == 1:
            profit = max(0 + self.func(ind + 1, 1, n, arr), arr[ind] + self.func(ind + 1, 0, n, arr))

        # Return the calculated profit
        return profit

    # Function to calculate the maximum profit earned 
    def stockBuySell(self, arr, n):
        if n == 0:
            return 0

        ans = self.func(0, 0, n, arr)
        
        # Return the maximum profit
        return ans

if __name__ == "__main__":
    n = 6
    arr = [7, 1, 5, 3, 6, 4]
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n))
class Solution {
    // Function to find the maximum profit earned using recursion
    func(ind, buy, n, arr) {
        // Base case 
        if (ind === n) {
            return 0;
        }

        let profit = 0;
        
        // We can buy the stock
        if (buy === 0) { 
            profit = Math.max(0 + this.func(ind + 1, 0, n, arr), (-1)*arr[ind] + this.func(ind + 1, 1, n, arr));
        }
        
        // We can sell the stock
        if (buy === 1) { 
            profit = Math.max(0 + this.func(ind + 1, 1, n, arr), arr[ind] + this.func(ind + 1, 0, n, arr));
        }

        // Return the calculated profit
        return profit;
    }

    // Function to calculate the maximum profit earned 
    stockBuySell(arr, n) {
        if (n === 0) 
            return 0;

        let ans = this.func(0, 0, n, arr);
        
        // Return the maximum profit
        return ans;
    }
}

function main() {
    const n = 6;
    const arr = [7, 1, 5, 3, 6, 4];
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n));
}

main();

Time Complexity: O(2^(N)), where N is the number of row. As, for each index, ther are two possible options.

Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.

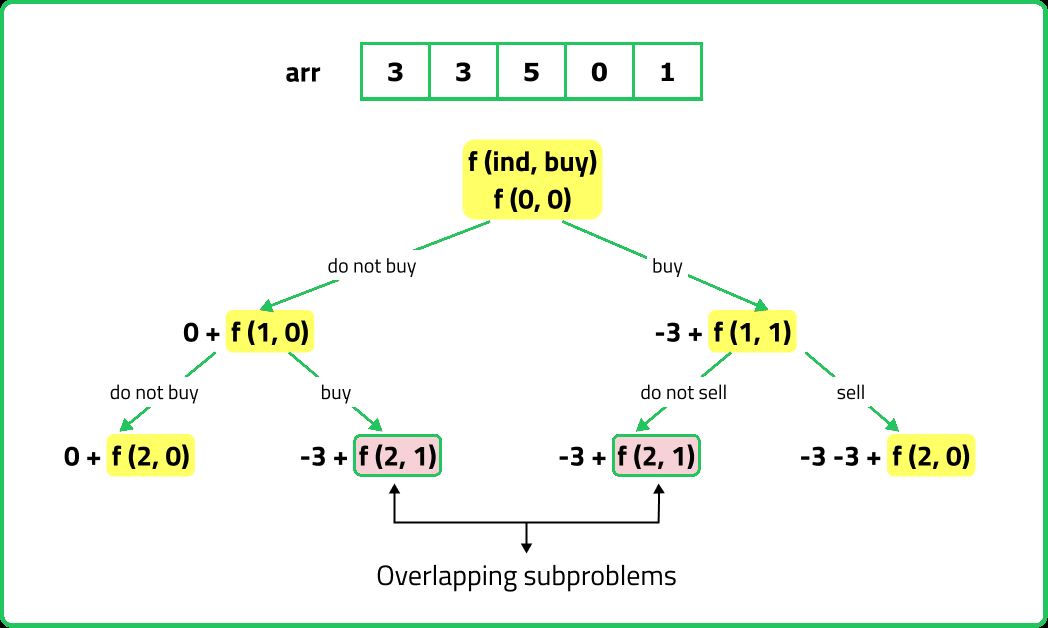
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][2]: As there are two changing parameters in the recursive solution, 'ind' and 'buy'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'buy' only two values possible 0, 1.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find the maximum profit earned using memoization
    int func(int ind, int buy, int n, vector<int> &arr, vector<vector<int>> &dp) {
        // Base case 
        if (ind == n) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy] != -1) {
            return dp[ind][buy];
        }
        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = max(0 + func(ind + 1, 0, n, arr, dp), (-1)*arr[ind] + func(ind + 1, 1, n, arr, dp));
        }
        
        //We can sell the stock
        if (buy == 1) { 
            profit = max(0 + func(ind + 1, 1, n, arr, dp), arr[ind] + func(ind + 1, 0, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        return dp[ind][buy] = profit;
    }
public:
    //Function to calculate the maximum profit earned 
    int stockBuySell(vector<int> &arr, int n) {
        if (n == 0) 
            return 0;
        // Initialize a DP table to memoize results
        vector<vector<int>> dp(n, vector<int>(2, -1));

        int ans = func(0, 0, n, arr, dp);
        
        //Return the maximum profit
        return ans;
    }
};
int main() {
    int n = 6;
    vector<int> arr = {7, 1, 5, 3, 6, 4};
    
    //Create an instance of Solution class
    Solution sol;

    // Call the stockBuySell function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n);

    return 0;
}


import java.util.*;

class Solution {
    // Function to find the maximum profit earned using memoization
    private int func(int ind, int buy, int n, int[] arr, int[][] dp) {
        // Base case 
        if (ind == n) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy] != -1) {
            return dp[ind][buy];
        }
        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = Math.max(0 + func(ind + 1, 0, n, arr, dp), (-1)*arr[ind] + func(ind + 1, 1, n, arr, dp));
        }
        
        // We can sell the stock
        if (buy == 1) { 
            profit = Math.max(0 + func(ind + 1, 1, n, arr, dp), arr[ind] + func(ind + 1, 0, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        return dp[ind][buy] = profit;
    }

    // Function to calculate the maximum profit earned 
    public int stockBuySell(int[] arr, int n) {
        if (n == 0) 
            return 0;
            
        // Initialize a DP table to memoize results
        int[][] dp = new int[n][2];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        int ans = func(0, 0, n, arr, dp);
        
        // Return the maximum profit
        return ans;
    }

    public static void main(String[] args) {
        int n = 6;
        int[] arr = {7, 1, 5, 3, 6, 4};
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n));
    }
}
class Solution:
    # Function to find maximum profit earned using memoization
    def func(self, ind, buy, n, arr, dp):
        # Base case 
        if ind == n:
            return 0
            
        """ If the result for this state has 
        already been calculated, return it"""
        if dp[ind][buy] != -1:
            return dp[ind][buy]
        
        profit = 0
        
        # We can buy the stock
        if buy == 0:
            profit = max(0 + self.func(ind + 1, 0, n, arr, dp), (-1)*arr[ind] + self.func(ind + 1, 1, n, arr, dp))
        
        # We can sell the stock
        if buy == 1:
            profit = max(0 + self.func(ind + 1, 1, n, arr, dp), arr[ind] + self.func(ind + 1, 0, n, arr, dp))
        
        """ Store the value in dp array and
        return the calculated profit"""
        dp[ind][buy] = profit
        return dp[ind][buy]

    # Function to calculate the maximum profit earned 
    def stockBuySell(self, arr, n):
        if n == 0:
            return 0
        # Initialize a DP table to memoize results
        dp = [[-1 for _ in range(2)] for _ in range(n)]

        ans = self.func(0, 0, n, arr, dp)
        
        # Return the maximum profit
        return ans

if __name__ == "__main__":
    n = 6
    arr = [7, 1, 5, 3, 6, 4]
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n))
class Solution {
    // Function to find maximum profit earned using memoization
    func(ind, buy, n, arr, dp) {
        // Base case 
        if (ind === n) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy] !== -1) {
            return dp[ind][buy];
        }
        let profit = 0;
        
        // We can buy the stock
        if (buy === 0) { 
            profit = Math.max(0 + this.func(ind + 1, 0, n, arr, dp), (-1)*arr[ind] + this.func(ind + 1, 1, n, arr, dp));
        }
        
        // We can sell the stock
        if (buy === 1) { 
            profit = Math.max(0 + this.func(ind + 1, 1, n, arr, dp), arr[ind] + this.func(ind + 1, 0, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        dp[ind][buy] = profit;
        return dp[ind][buy];
    }

    // Function to calculate the maximum profit earned 
    stockBuySell(arr, n) {
        if (n === 0) 
            return 0;
        // Initialize a DP table to memoize results
        let dp = new Array(n).fill().map(() => new Array(2).fill(-1));

        let ans = this.func(0, 0, n, arr, dp);
        
        // Return the maximum profit
        return ans;
    }
}
    const n = 6;
    const arr = [7, 1, 5, 3, 6, 4];
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n));

Complexity Analysis:

Time Complexity: O(N*2), There are N*2 states, therefore at max ‘N*2’ new problems will be solved.

Space Complexity:O(N*2) + O(N), As we are using a recursion stack space of O(N) and a 2D array O(N*2).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n+1][2]: As there are two changing parameters in the recursive solution, 'ind' and 'buy'. The maximum value 'ind' can attain is (n) and including 0 its n+1, where n is the size of array and for 'buy' only two values possible 0, 1.

Setting Base Cases in the Array: In the recursive code, our base condition was when If ind == n, it means we have finished trading on all days, and there is no more money that we can get, therefore simply return 0. As this is the last row, so set dp[n][0] = dp[n][1] = 0(the case when we had exhausted the number of days of the stock market).

Iterative Computation Using Loops: Set two nested for loops, the outer loop (for variable ind) moves from n-1 to 0 and the inner loop (for variable buy) moves from 0 to 1. In every iteration, calculate the value according to the memoization logic.

Choosing the maximum: As we are looking to maximize the profit earned, return the maximum value in all the cases as discussed in memoization approach.

Returning the answer: The element dp[0][0] of the dp array is returned because it holds the optimal solution to the entire problem after the computation has been completed.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find maximum profit earned using tabulation
    int func(vector<int> &arr, int n) {
        // Create a DP table to memoize results
        vector<vector<int>> dp(n + 1, vector<int>(2, -1));

        // Base condition
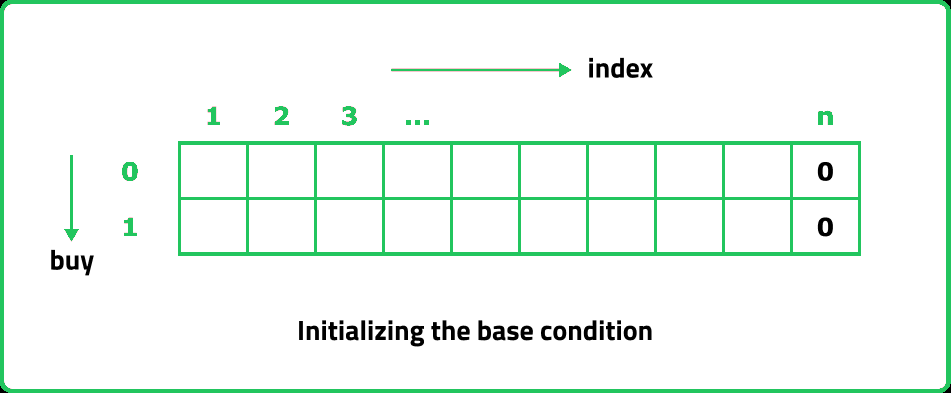
        dp[n][0] = dp[n][1] = 0;

        int profit;

        // Loop through the array in reverse order
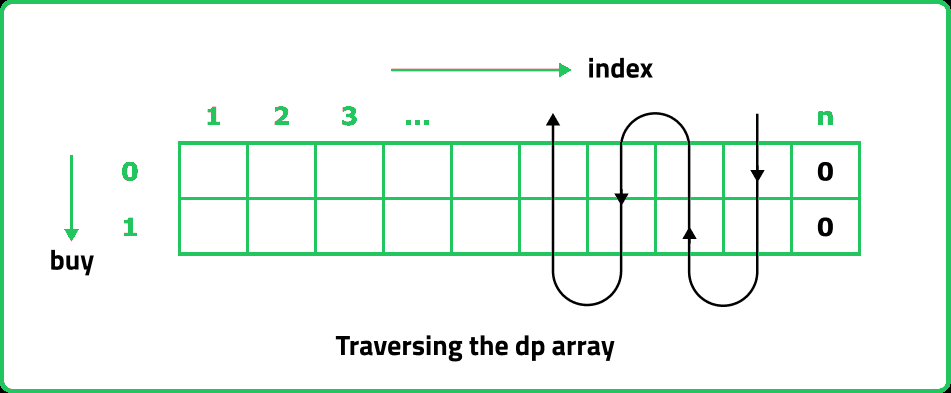
        for (int ind = n - 1; ind >= 0; ind--) {
            for (int buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy == 0) { 
                    profit = max(0 + dp[ind + 1][0], (-1)*arr[ind] + dp[ind + 1][1]);
                }
            
                // We can sell the stock
                if (buy == 1) { 
                    profit = max(0 + dp[ind + 1][1], arr[ind] + dp[ind + 1][0]);
                }

                dp[ind][buy] = profit;
            }
        }

        /* The maximum profit is stored in
        dp[0][0] after all calculations*/
        return dp[0][0];
    }
public:
    //Function to calculate the maximum profit earned
    int stockBuySell(vector<int> &arr, int n){
        //Return the maximum profit
        return func(arr, n);
    }
};
int main() {
    int n = 6;
    vector<int> arr = {7, 1, 5, 3, 6, 4};
    
    //Create an instance of Solution class
    Solution sol;

    // Call the getMaximumProfit function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n);

    return 0;
}
import java.util.*;

class Solution {
    // Function to find maximum profit earned using tabulation
    private int func(int[] arr, int n) {
        // Create a DP table to memoize results
        int[][] dp = new int[n + 1][2];

        // Base condition
        dp[n][0] = dp[n][1] = 0;

        int profit = 0;

        // Loop through the array in reverse order
        for (int ind = n - 1; ind >= 0; ind--) {
            for (int buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy == 0) { 
                    profit = Math.max(0 + dp[ind + 1][0], (-1)*arr[ind] + dp[ind + 1][1]);
                }
            
                // We can sell the stock
                if (buy == 1) { 
                    profit = Math.max(0 + dp[ind + 1][1], arr[ind] + dp[ind + 1][0]);
                }

                dp[ind][buy] = profit;
            }
        }

        /* The maximum profit is stored in
        dp[0][0] after all calculations*/
        return dp[0][0];
    }

    // Function to calculate the maximum profit earned
    public int stockBuySell(int[] arr, int n){
        // Return the maximum profit
        return func(arr, n);
    }

    public static void main(String[] args) {
        int n = 6;
        int[] arr = {7, 1, 5, 3, 6, 4};
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n));
    }
}
class Solution:
    # Function to find maximum profit earned using tabulation
    def func(self, arr, n):
        # Create a DP table to memoize results
        dp = [[-1 for _ in range(2)] for _ in range(n + 1)]

        # Base condition
        dp[n][0] = dp[n][1] = 0

        # Loop through the array in reverse order
        for ind in range(n - 1, -1, -1):
            for buy in range(2):
                # We can buy the stock
                if buy == 0:
                    profit = max(0 + dp[ind + 1][0], (-1)*arr[ind] + dp[ind + 1][1])
                
                # We can sell the stock
                if buy == 1:
                    profit = max(0 + dp[ind + 1][1], arr[ind] + dp[ind + 1][0])

                dp[ind][buy] = profit

        """ The maximum profit is stored in 
        dp[0][0] after all calculations"""
        return dp[0][0]

    # Function to calculate the maximum profit earned
    def stockBuySell(self, arr, n):
        # Return the maximum profit
        return self.func(arr, n)

if __name__ == "__main__":
    n = 6
    arr = [7, 1, 5, 3, 6, 4]
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n))
class Solution {
    // Function to find maximum profit earned using tabulation
    func(arr, n) {
        // Create a DP table to memoize results
        let dp = new Array(n + 1).fill().map(() => new Array(2).fill(-1));

        // Base condition
        dp[n][0] = dp[n][1] = 0;

        let profit;

        // Loop through the array in reverse order
        for (let ind = n - 1; ind >= 0; ind--) {
            for (let buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy === 0) { 
                    profit = Math.max(0 + dp[ind + 1][0], (-1)*arr[ind] + dp[ind + 1][1]);
                }
            
                // We can sell the stock
                if (buy === 1) { 
                    profit = Math.max(0 + dp[ind + 1][1], arr[ind] + dp[ind + 1][0]);
                }

                dp[ind][buy] = profit;
            }
        }

        /* The maximum profit is stored in
        dp[0][0] after all calculations*/
        return dp[0][0];
    }

    // Function to calculate the maximum profit earned
    stockBuySell(arr, n) {
        // Return the maximum profit
        return this.func(arr, n);
    }
}

function main() {
    const n = 6;
    const arr = [7, 1, 5, 3, 6, 4];
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n));
}

main();

Complexity Analysis:

Time Complexity: O(N*2), As, here are two nested loops that account for O(N*2) complexity.

Space Complexity:O(N*2), As a 2D array of size N*2 is used.

If we observe the relation obtained in the tabulation, dp[ind][buy] = max( dp[ind+1][buy] , max( dp[ind+1][!buy]), we see that to calculate a value of a cell of the dp array, only the next column values are needed(say ahead). So, we don’t need to store an entire 2-D array. Hence the tabulation code can be space optimized.

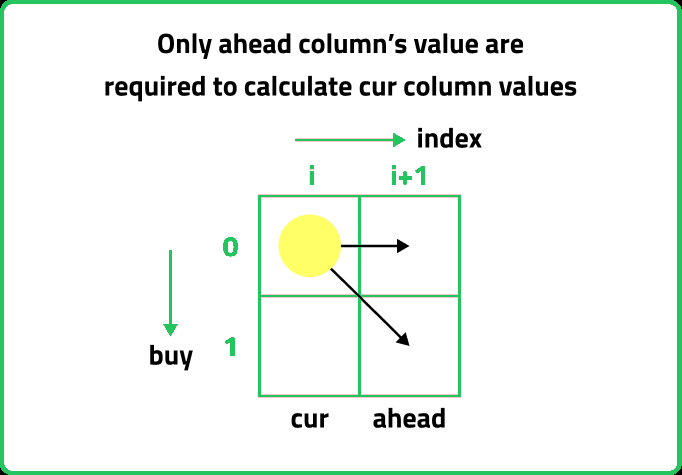
The Steps to space optimize the tabulation approach are as follows:

Declare two arrays to store the profits ahead of the current position (0 for not holding, 1 for holding).

For the case condition, set ahead[0] and ahead[1] to 0, as when there are no stocks left, the profit is 0.

Then, initiate two nested for loops to calculate the 'cur' column values. Replace dp[ind] with 'cur' and dp[ind+1] with 'ahead' in our memoization code.

After the inner loop execution, set 'ahead' as 'cur' for the next outer loop iteration. At last, return cur[0] as our answer.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find maximum profit using space optimization
    int func(vector<int> &arr, int n) {
        /* Declare two arrays to store the profits ahead of 
        current position (0 for not holding, 1 for holding)*/
        vector<long> ahead(2, 0);
        vector<long> cur(2, 0);

        // Base condition
        ahead[0] = ahead[1] = 0;

        int profit;

        // Loop through the array in reverse order
        for (int ind = n - 1; ind >= 0; ind--) {
            for (int buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy == 0) { 
                    profit = max(0 + ahead[0], (-1)*arr[ind] + ahead[1]);
                }
                // We can sell the stock
                if (buy == 1) { 
                    profit = max(0 + ahead[1], arr[ind] + ahead[0]);
                }
                cur[buy] = profit;
            }
            // Update the "ahead" array with the current values
            ahead = cur; 
        }

        // Maximum profit is stored in cur[0] 
        return cur[0];
    }
public:
    //Function to find out the maximum profit earned
    int stockBuySell(vector<int> &arr, int n){
        //Return the maximum profit
        return func(arr, n);
    }
};
int main() {
    int n = 6;
    vector<int> arr = {7, 1, 5, 3, 6, 4};
    
    //Create an instance of Solution class
    Solution sol;

    // Call the getMaximumProfit function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n);

    return 0;
}

import java.util.*;

class Solution {
    // Function to find maximum profit using space optimization
    private int func(int[] arr, int n) {
        /* Declare two arrays to store the profits ahead of 
        current position (0 for not holding, 1 for holding)*/
        int[] ahead = new int[2];
        int[] cur = new int[2];

        // Base condition
        ahead[0] = ahead[1] = 0;

        int profit = 0;

        // Loop through the array in reverse order
        for (int ind = n - 1; ind >= 0; ind--) {
            for (int buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy == 0) { 
                    profit = Math.max(0 + ahead[0], (-1)*arr[ind] + ahead[1]);
                }
                // We can sell the stock
                if (buy == 1) { 
                    profit = Math.max(0 + ahead[1], arr[ind] + ahead[0]);
                }
                cur[buy] = profit;
            }
            // Update the "ahead" array with the current values
            ahead = cur;
        }

        // Maximum profit is stored in cur[0] 
        return cur[0];
    }

    // Function to calculate the maximum profit earned
    public int stockBuySell(int[] arr, int n){
        // Return the maximum profit
        return func(arr, n);
    }

    public static void main(String[] args) {
        int n = 6;
        int[] arr = {7, 1, 5, 3, 6, 4};
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n));
    }
}
class Solution:
    # Function to find maximum profit using space optimization
    def func(self, arr, n):
        """Declare two arrays to store the profits ahead of 
        current position (0 for not holding, 1 for holding)"""
        ahead = [0, 0]
        cur = [0, 0]

        # Base condition
        ahead[0] = ahead[1] = 0

        # Loop through the array in reverse order
        for ind in range(n - 1, -1, -1):
            for buy in range(2):
                # We can buy the stock
                if buy == 0:
                    profit = max(0 + ahead[0], (-1)*arr[ind] + ahead[1])
                
                # We can sell the stock
                if buy == 1:
                    profit = max(0 + ahead[1], arr[ind] + ahead[0])
                
                cur[buy] = profit
            
            # Update the "ahead" array with the current values
            ahead = cur[:]
        
        # Maximum profit is stored in cur[0] 
        return cur[0]

    # Function to calculate the maximum profit earned
    def stockBuySell(self, arr, n):
        # Return the maximum profit
        return self.func(arr, n)

if __name__ == "__main__":
    n = 6
    arr = [7, 1, 5, 3, 6, 4]
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n))
class Solution {
    // Function to find maximum profit using space optimization
    func(arr, n) {
        /* Declare two arrays to store the profits ahead of 
        current position (0 for not holding, 1 for holding)*/
        let ahead = [0, 0];
        let cur = [0, 0];

        // Base condition
        ahead[0] = ahead[1] = 0;

        let profit;

        // Loop through the array in reverse order
        for (let ind = n - 1; ind >= 0; ind--) {
            for (let buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy === 0) { 
                    profit = Math.max(0 + ahead[0], (-1)*arr[ind] + ahead[1]);
                }
                // We can sell the stock
                if (buy === 1) { 
                    profit = Math.max(0 + ahead[1], arr[ind] + ahead[0]);
                }
                cur[buy] = profit;
            }
            // Update the "ahead" array with current values
            ahead[0] = cur[0];
            ahead[1] = cur[1];
        }

        // Maximum profit is stored in ahead[0] 
        return ahead[0];
    }

    // Function to calculate the maximum profit earned
    stockBuySell(arr, n) {
        // Return the maximum profit
        return this.func(arr, n);
    }
}

function main() {
    const n = 6;
    const arr = [7, 1, 5, 3, 6, 4];
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n));
}

main();

Complexity Analysis:

Time Complexity: O(N*2), As, here are two nested loops that account for O(N*2) complexity.

Space Complexity:O(1), As we are using an external array of size ‘2’.

Problem List

Best time to buy and sell stock II

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

The Steps to space optimize the tabulation approach are as follows:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code