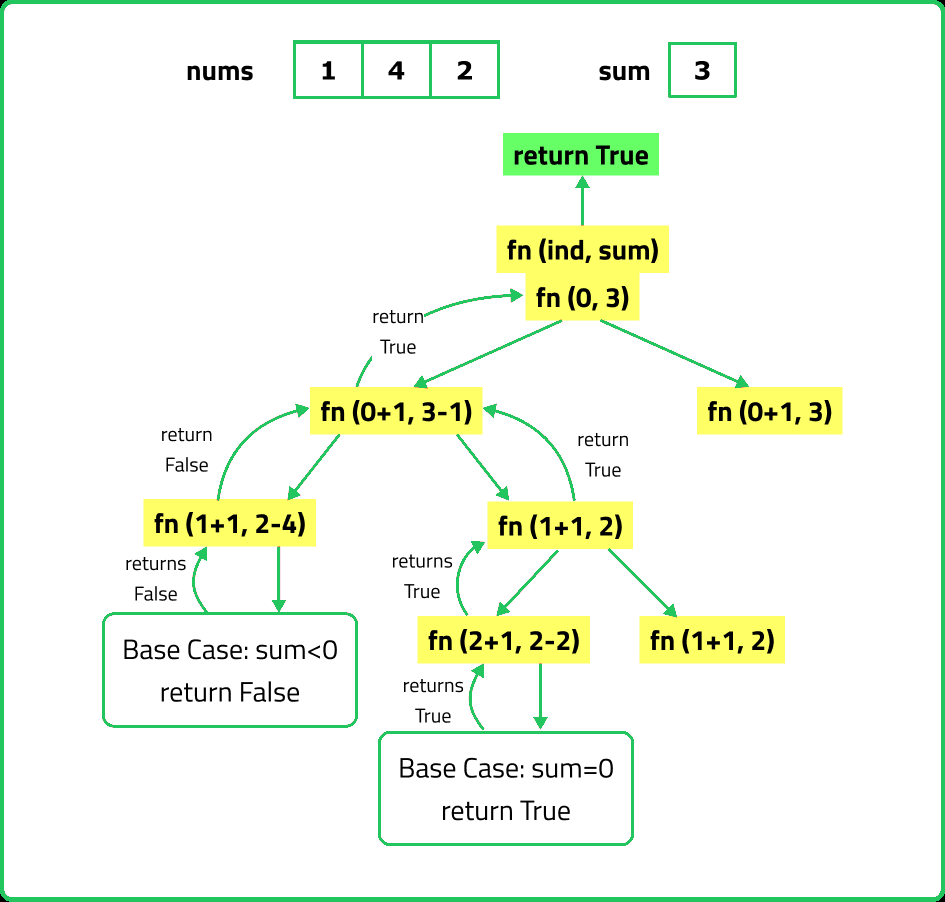
Check if there exists a subsequence with sum K
Recursion
Subsequence Pattern Problems
Easy
Given an array nums and an integer k. Return true if there exist subsequences such that the sum of all elements in subsequences is equal to k else false.
Examples:
Input : nums = [1, 2, 3, 4, 5] , k = 8
Output : Yes
Explanation : The subsequences like [1, 2, 5] , [1, 3, 4] , [3, 5] sum up to 8.
Input : nums = [4, 3, 9, 2] , k = 10
Output : No
Explanation : No subsequence can sum up to 10.
Input : nums = [1, 10, 4, 5] , k = 16
Constraints
- 1 <= nums.length <= 20
- 1 <= nums[i] <= 100
- 1 <= k <= 2000
Hints
- Explore all possible subsequences recursively and count the valid ones where the sum equals k. Use a DP table where dp[j] represents the number of subsequences with sum j.
- Use recursion to explore all subsequences:Count the number of valid subsequences where the sum equals k.
Company Tags
JPMorgan Chase
Intel
MongoDB
Bain & Company
IBM
Epic Systems
Wayfair
Databricks
Boston Consulting Group
Docker
Epic Games
Micron Technology
Roche
Robinhood
Unity Technologies
Activision Blizzard
Visa
Optum
Stripe
Bloomberg
Twilio
DoorDash
Freshworks
Byju's
AMD
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro