BST iterator
- This concept of BSTIterator is widely used in databases and file systems
- In such systems, data is often stored in a binary search tree format to allow efficient search, insertion, and deletion operations
- An in-order BST iterator, like the one in the problem, allows developers to efficiently traverse through this data in a sorted manner, which can markedly improve the performance of operations like range queries, sorting and displaying data
- This functionality is typically offered by databases' 'cursor' abstraction, and is fundamental to SQL operations
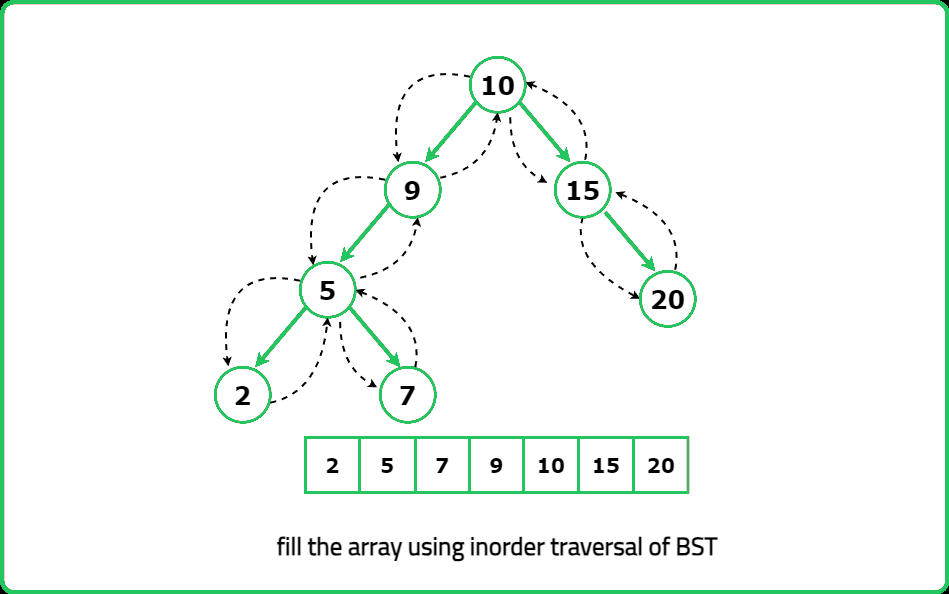
Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):
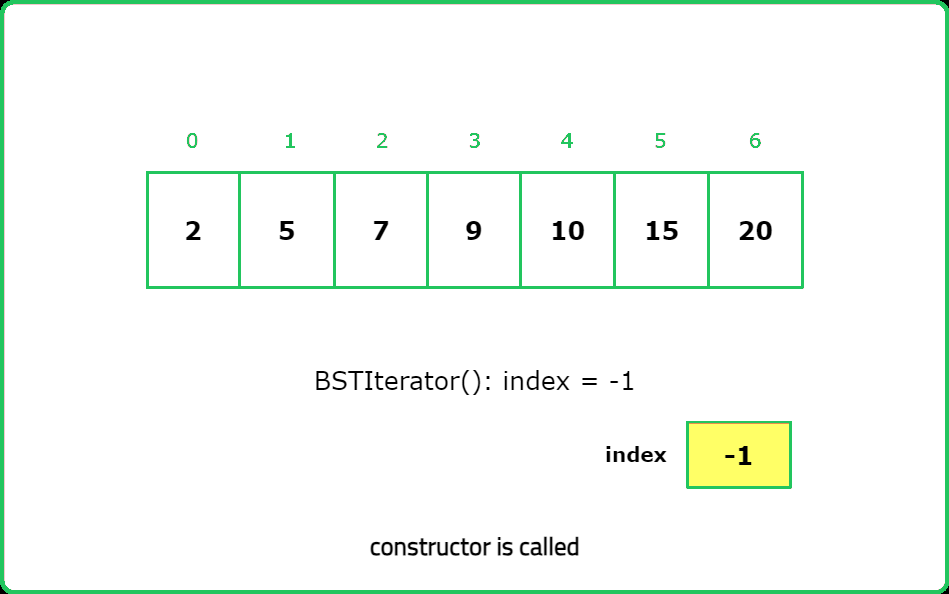
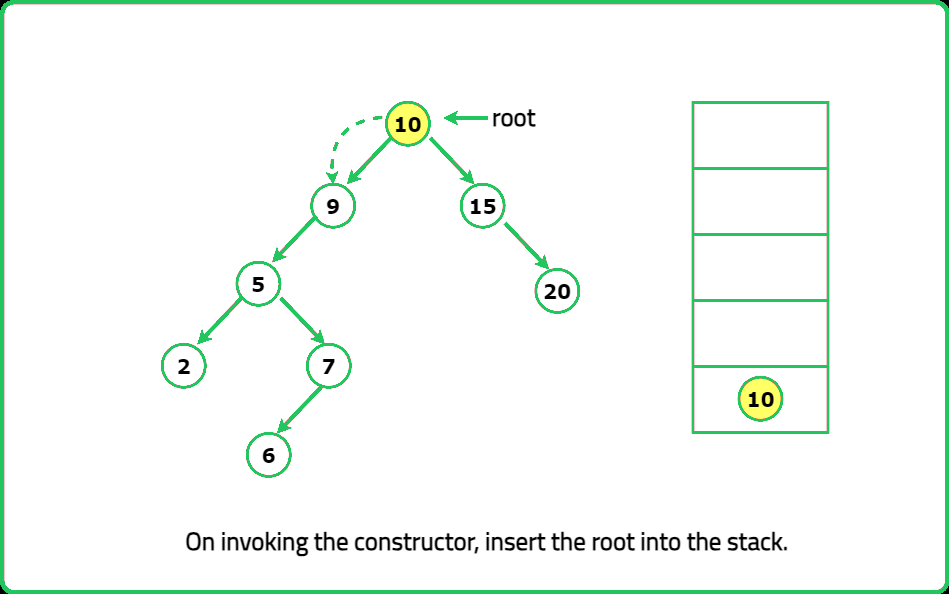
- BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
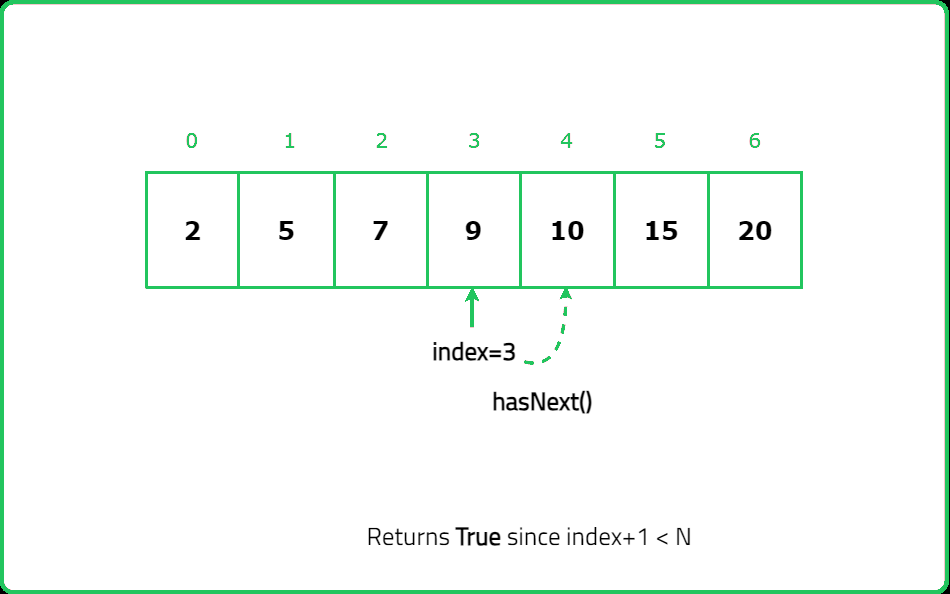
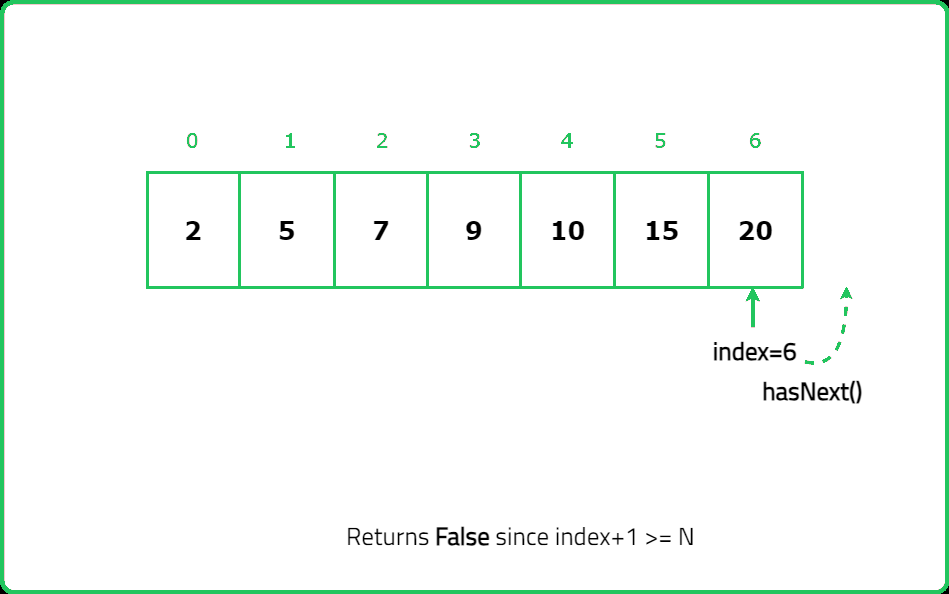
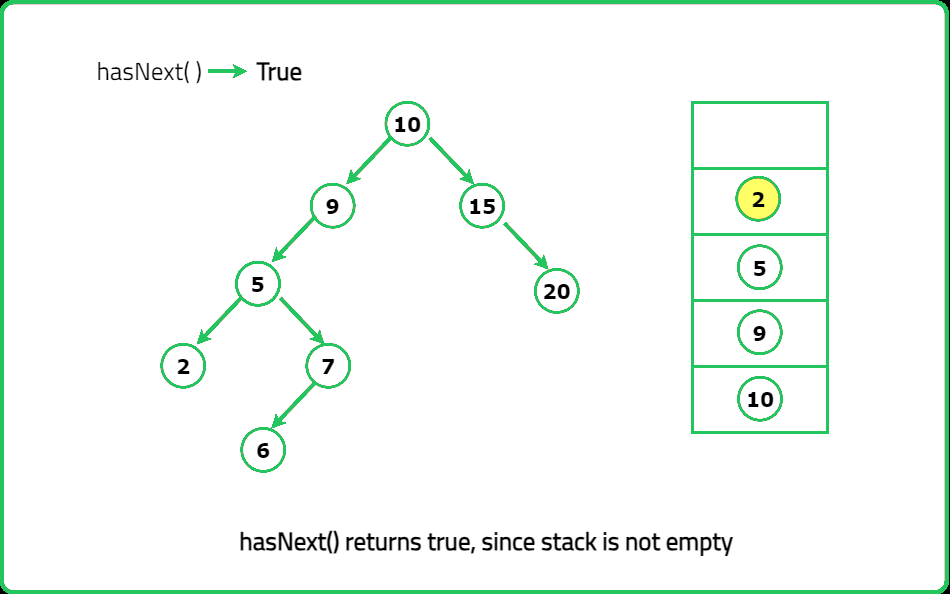
- boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
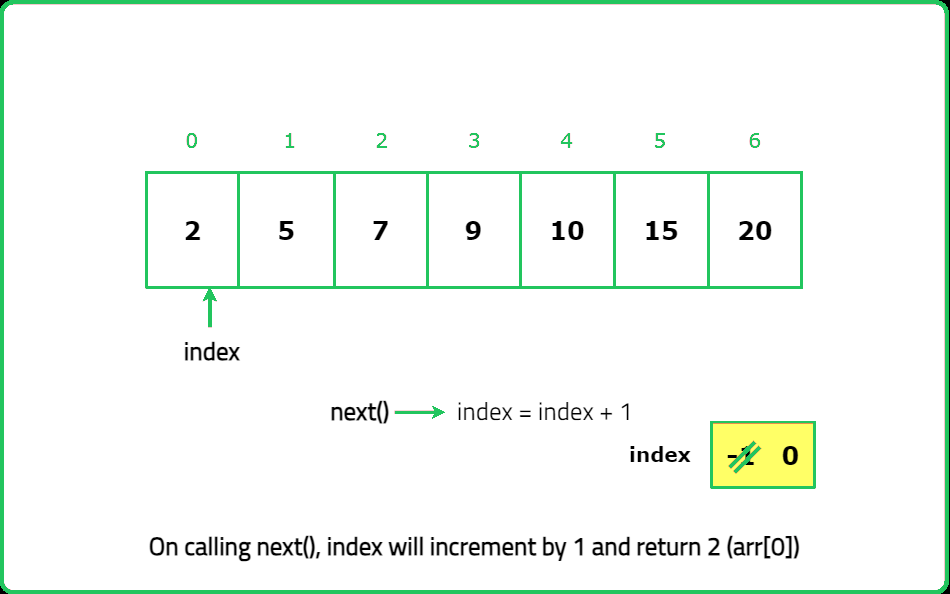
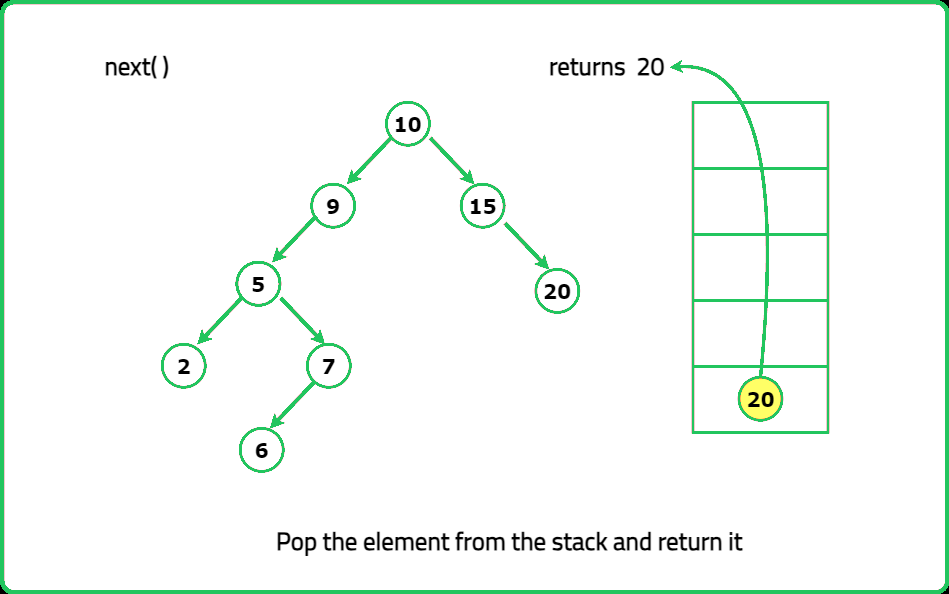
- int next() Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to the next() will return the smallest element in the BST.
Assume that the next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when the next() is called.
Examples:
Input : [ "BSTIterator" , "next" , "next" , "hasNext" , "next" , "hasNext" , "next" , "hasNext" , "next" , "hasNext" ] , root = [7, 3, 15, null, null, 9, 20]
Output : [3, 7, true, 9, true, 15, true, 20, false]
Explanation :
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
Input : [ "BSTIterator" , "next" , "next" , "next", "hasNext" , "next" , "hasNext" ] , root = [7, 3, 15, null, null, 9, 20]
Output : [3, 7, 9, true, 15, true]
Explanation :
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
Input : [ "BSTIterator" , "next" , "next", "next", "next", "next" , "hasNext" ] , root = [7, 3, 15, null, null, 9, 20]
Constraints
- 1 <= Number of Nodes <= 104
- At most 104 calls will be made to next and hasNext.
- 0 <= Node.val <= 105
Hints
- "Perform an inorder traversal during initialization and store the elements in an array. next() simply returns the next element from the stored list. hasNext() checks if more elements are available."
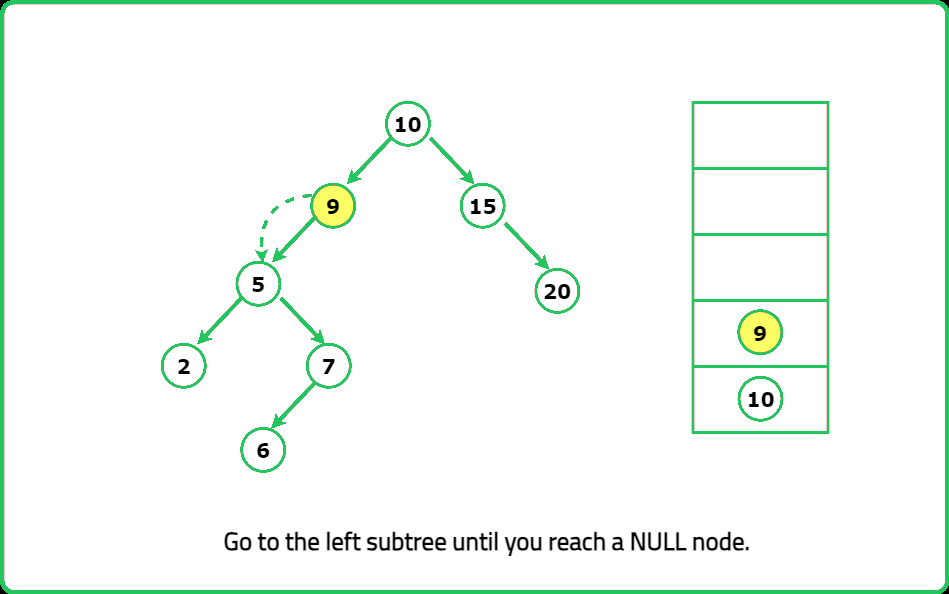
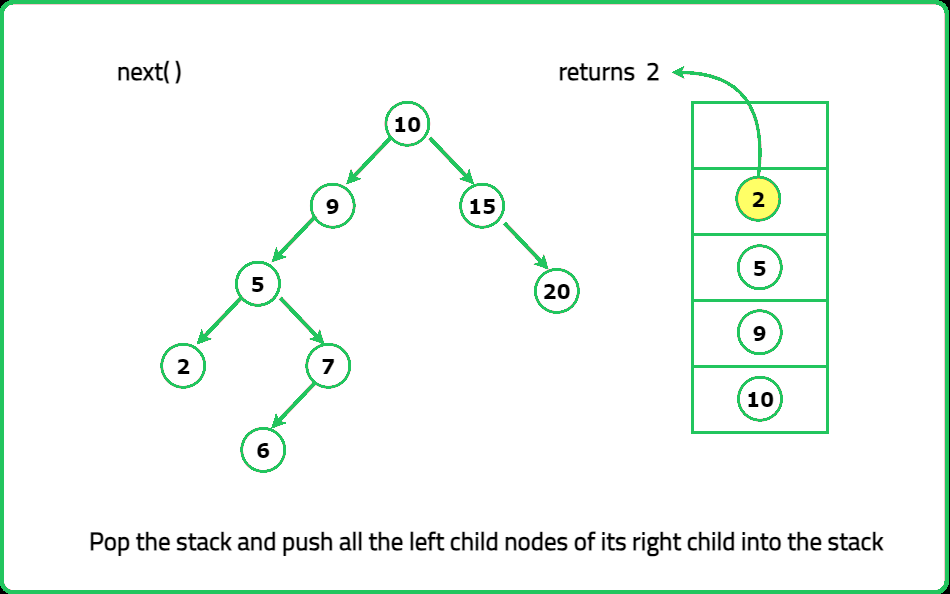
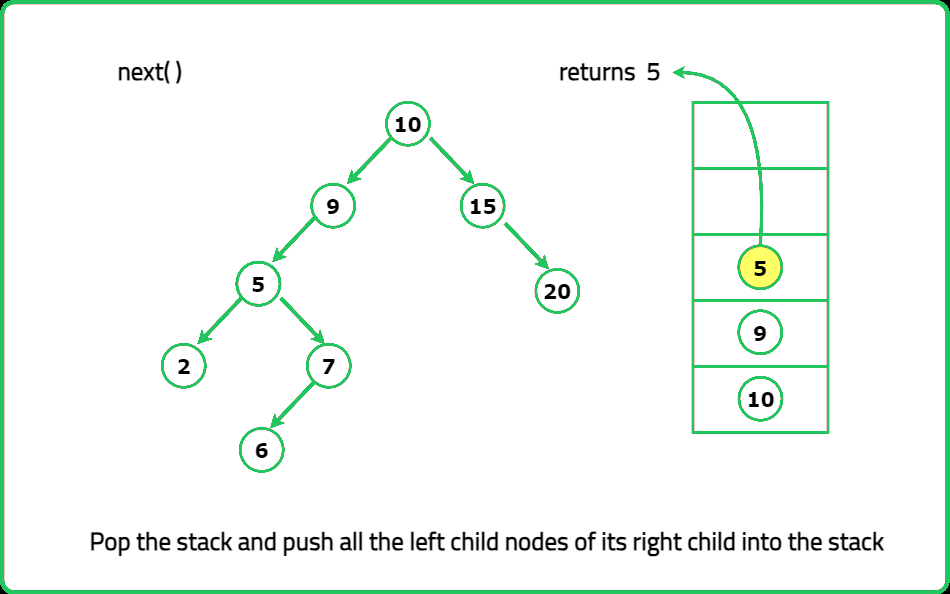
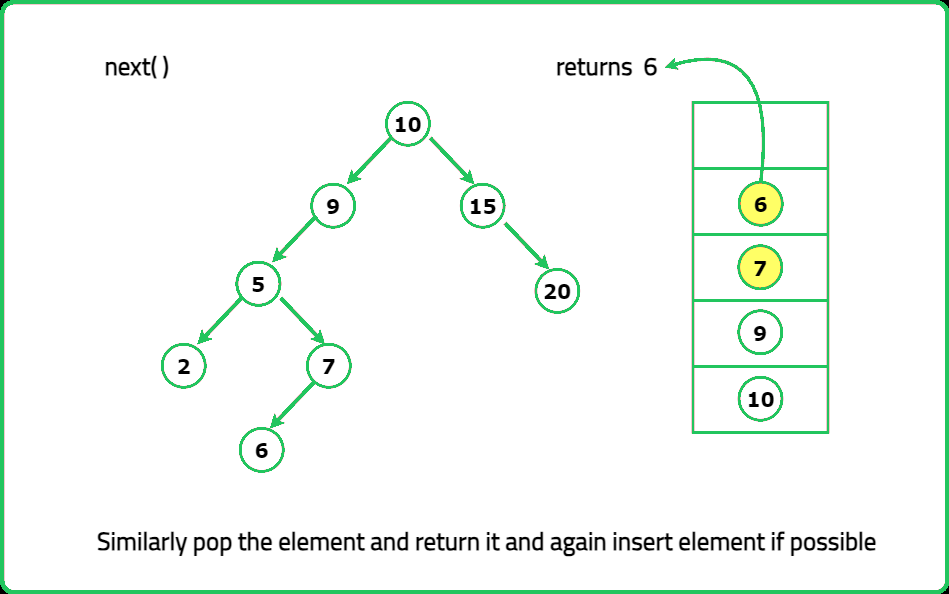
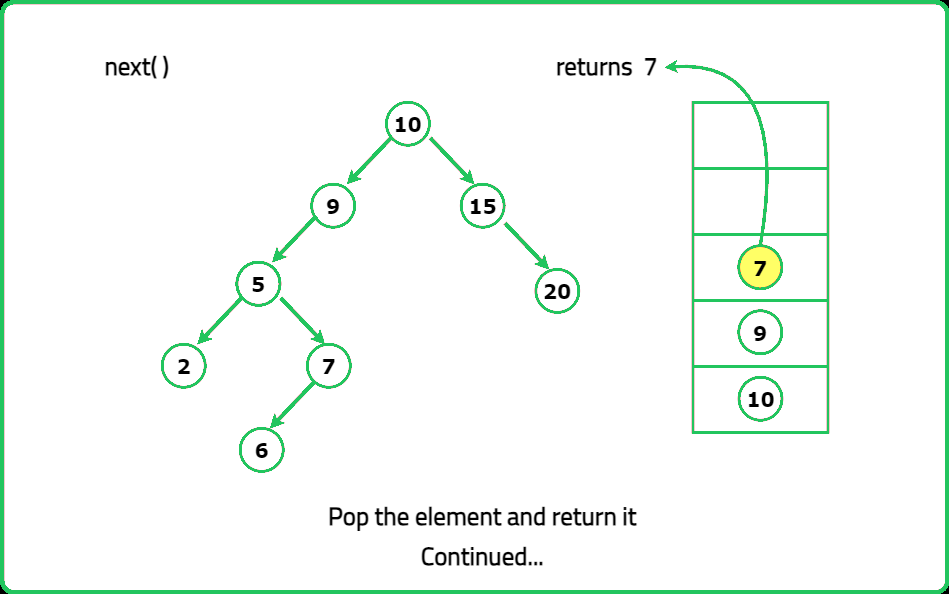
- "Instead of storing all elements, use a stack to simulate recursion. Push all left children first. When next() is called: Pop the top element. Push its right subtree’s leftmost path into the stack."