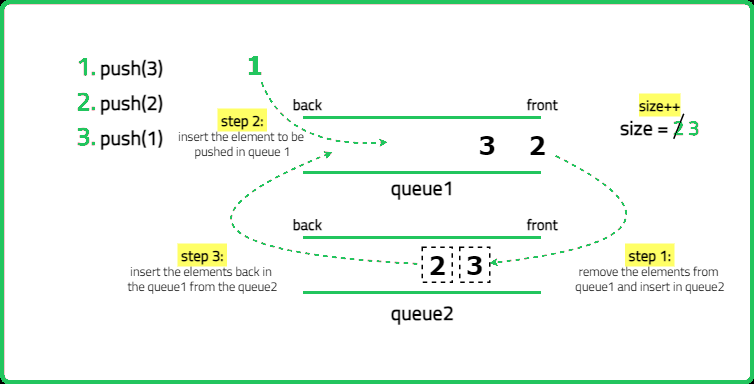
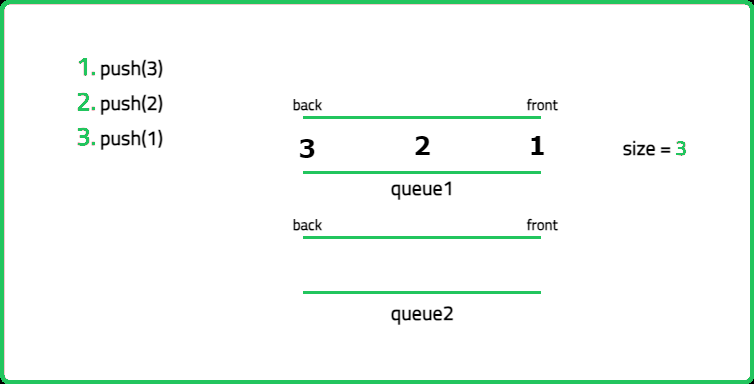
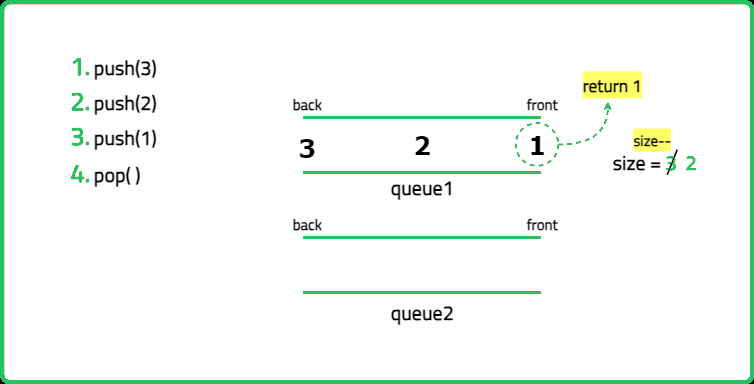
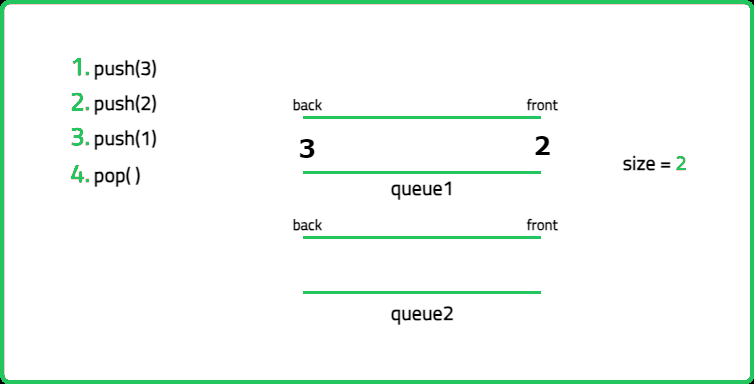
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
#include <bits/stdc++.h>
using namespace std;
// Stack implementation using Queue
class QueueStack {
// Queue
queue<int> q;
public:
// Method to push element in the stack
void push(int x) {
// Get size
int s = q.size();
// Add element
q.push(x);
// Move elements before new element to back
for (int i = 0; i < s; i++) {
q.push(q.front());
q.pop();
}
}
// Method to pop element from stack
int pop() {
// Get front element
int n = q.front();
// Remove front element
q.pop();
// Return removed element
return n;
}
// Method to return the top of stack
int top() {
// Return front element
return q.front();
}
// Method to check if the stack is empty
bool isEmpty() {
return q.empty();
}
};
int main() {
QueueStack st;
// List of commands
vector<string> commands = {"QueueStack", "push", "push",
"pop", "top", "isEmpty"};
// List of inputs
vector<vector<int>> inputs = {{}, {4}, {8}, {}, {}, {}};
for (int i = 0; i < commands.size(); ++i) {
if (commands[i] == "push") {
st.push(inputs[i][0]);
cout << "null ";
} else if (commands[i] == "pop") {
cout << st.pop() << " ";
} else if (commands[i] == "top") {
cout << st.top() << " ";
} else if (commands[i] == "isEmpty") {
cout << (st.isEmpty() ? "true" : "false") << " ";
} else if (commands[i] == "QueueStack") {
cout << "null ";
}
}
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
import java.util.*;
// Stack implementation using Queue
class QueueStack {
// Queue
Queue<Integer> q = new LinkedList<>();
// Method to push element in the stack
public void push(int x) {
// Get size
int s = q.size();
// Add element
q.add(x);
// Move elements before new element to back
for (int i = 0; i < s; i++) {
q.add(q.poll());
}
}
// Method to pop element from stack
public int pop() {
// Get front element
int n = q.peek();
// Remove front element
q.poll();
// Return removed element
return n;
}
// Method to return the top of stack
public int top() {
// Return front element
return q.peek();
}
// Method to check if the stack is empty
public boolean isEmpty() {
return q.isEmpty();
}
}
// Main class
class Main {
public static void main(String[] args) {
QueueStack st = new QueueStack();
// Array of commands
String[] commands = {"QueueStack", "push", "push",
"pop", "top", "isEmpty"};
int[][] inputs = {{}, {4}, {8}, {}, {}, {}};
for (int i = 0; i < commands.length; ++i) {
switch (commands[i]) {
case "push":
st.push(inputs[i][0]);
System.out.print("null ");
break;
case "pop":
System.out.print(st.pop() + " ");
break;
case "top":
System.out.print(st.top() + " ");
break;
case "isEmpty":
System.out.print(st.isEmpty() ? "true " : "false ");
break;
case "QueueStack":
System.out.print("null ");
break;
}
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
from queue import Queue
# Stack implementation using Queue
class QueueStack:
def __init__(self):
# Queue
self.q = Queue()
# Method to push element in the stack
def push(self, x):
# Get size
s = self.q.qsize()
# Add element
self.q.put(x)
# Move elements before new element to back
for _ in range(s):
self.q.put(self.q.get())
# Method to pop element from stack
def pop(self):
# Get front element
n = self.q.queue[0]
# Remove front element
self.q.get()
# Return removed element
return n
# Method to return the top of stack
def top(self):
# Return front element
return self.q.queue[0]
# Method to check if the stack is empty
def isEmpty(self):
return self.q.empty()
if __name__ == "__main__":
st = QueueStack()
# List of commands
commands = ["QueueStack", "push", "push", "pop", "top", "isEmpty"]
inputs = [[], [4], [8], [], [], []]
for i in range(len(commands)):
if commands[i] == "push":
st.push(inputs[i][0])
print("null", end=" ")
elif commands[i] == "pop":
print(st.pop(), end=" ")
elif commands[i] == "top":
print(st.top(), end=" ")
elif commands[i] == "isEmpty":
print("true" if st.isEmpty() else "false", end=" ")
elif commands[i] == "QueueStack":
print("null", end=" ")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
// Stack implementation using Queue
class QueueStack {
constructor() {
// Queue
this.q = [];
}
// Method to push element in the stack
push(x) {
// Get size
let s = this.q.length;
// Add element
this.q.push(x);
// Move elements before new element to back
for (let i = 0; i < s; i++) {
this.q.push(this.q.shift());
}
}
// Method to pop element from stack
pop() {
// Get front element
let n = this.q[0];
// Remove front element
this.q.shift();
// Return removed element
return n;
}
// Method to return the top of stack
top() {
// Return front element
return this.q[0];
}
// Method to check if the stack is empty
isEmpty() {
return this.q.length === 0;
}
}
const st = new QueueStack();
// List of commands
const commands = ["QueueStack", "push", "push", "pop", "top", "isEmpty"];
const inputs = [[], [4], [8], [], [], []];
for (let i = 0; i < commands.length; ++i) {
switch (commands[i]) {
case "push":
st.push(inputs[i][0]);
console.log("null ");
break;
case "pop":
console.log(st.pop() + " ");
break;
case "top":
console.log(st.top() + " ");
break;
case "isEmpty":
console.log(st.isEmpty() ? "true " : "false ");
break;
case "QueueStack":
console.log("null ");
break;
}
}