Majority Element-II

Intuition

The naive way is to use nested loops to count the occurrences of each of the elements and if the count is greater than one third of the size of array, include the element in the answer.

Can there be more than 2 majority elements ? Let's understand the scenario!

To understand why there can't be more than two majority elements (elements that appear more than n/3 times) in an array of size n, let's use a simple mathematical reasoning. A majority element in this context is defined as an element that appears more than n/3 times in the array. For an element to be a majority element, it must appear more than n/3 times. Let's assume there are more than two such majority elements. Let's denote these elements as A, B, and C.

Since each of these elements appears more than n/3 times, the combined frequency of these three elements would be: frequency of 𝐴 + frequency of 𝐵 + frequency of 𝐶 > 𝑛/3 + 𝑛/3 + 𝑛/3 = 𝑛

Now, the total number of occurrences of all elements in the array cannot exceed n, the size of the array. This means the combined frequency of any three elements each appearing more than n/3 times would exceed the total size of the array, which is a contradiction. Therefore, it's mathematically impossible for there to be more than two elements in the array that each appear more than n/3 times.

Approach

Iterate in the array to select the elements of the array one by one. Now, for each unique element, run another loop and count its occurrence in the given array. If any element occurs more than the floor of (N/3), include it in our answer.

While traversing if any element that is already included in our answer is found, just skip it. When the answer array size is already 2, break out of loop, as there cant be more than 2 elements.

Return the answer array or -1 if no such element is found.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find majority elements in an array
    vector<int> majorityElementTwo(vector<int>& nums) {
        
        // Size of the array
        int n = nums.size(); 
        
        // List of answers
        vector<int> result;
        
         for (int i = 0; i < n; i++) {
             
        /*Checking if nums[i] is not 
        already part of the answer*/
        if (result.size() == 0 || result[0] != nums[i]) {
            
            int cnt = 0;
            
            for (int j = 0; j < n; j++) {
                // counting the frequency of nums[i]
                if (nums[j] == nums[i]) {
                    cnt++;
                }
            }

            // check if frquency is greater than n/3:
            if (cnt > (n / 3))
                result.push_back(nums[i]);
        }
        
        //if result size is equal to 2 break out of loop
        if (result.size() == 2) break;
    }
    
    //return the majority elements
    return result;
    }
};

int main() {
    vector<int> arr = {11, 33, 33, 11, 33, 11};
    
    // Create an instance of Solution class
    Solution sol;

    vector<int> ans = sol.majorityElementTwo(arr);
    
    // Print the majority elements found
    cout << "The majority elements are: ";
    for (auto it : ans) {
        cout << it << " ";
    }
    cout << "\n";

    return 0;
}
import java.util.*;

class Solution {
    // Function to find majority elements in an array
    public List<Integer> majorityElementTwo(int[] nums) {
        // Size of the array
        int n = nums.length;
        
        // List of answers
        List<Integer> result = new ArrayList<>();
        
        for (int i = 0; i < n; i++) {
            /* Checking if nums[i] is not 
            already part of the answer */
            
            if (result.size() == 0 || result.get(0) != nums[i]) {
                
                int cnt = 0;
                
                for (int j = 0; j < n; j++) {
                    // counting the frequency of nums[i]
                    if (nums[j] == nums[i]) {
                        cnt++;
                    }
                }
                
                // check if frequency is greater than n/3
                if (cnt > (n / 3)) {
                    result.add(nums[i]);
                }
            }
            
            // if result size is equal to 2 break out of loop
            if (result.size() == 2) {
                break;
            }
        }
        
        // return the majority elements
        return result;
    }
    
    public static void main(String[] args) {
        int[] arr = {11, 33, 33, 11, 33, 11};
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        List<Integer> ans = sol.majorityElementTwo(arr);
        
        // Print the majority elements found
        System.out.print("The majority elements are: ");
        for (int it : ans) {
            System.out.print(it + " ");
        }
        System.out.println();
    }
}
from typing import List

class Solution:
    # Function to find majority elements in an array
    def majorityElementTwo(self, nums: List[int]) -> List[int]:
        
        # Size of the array
        n = len(nums)
        
        # List of answers
        result = []
        
        for i in range(n):
            """ Checking if nums[i] is not 
            already part of the answer """
            if len(result) == 0 or result[0] != nums[i]:
                
                cnt = 0
                
                for j in range(n):
                    # counting the frequency of nums[i]
                    if nums[j] == nums[i]:
                        cnt += 1
                
                # check if frequency is greater than n/3
                if cnt > (n // 3):
                    result.append(nums[i])
                
            # if result size is equal to 2 break out of loop
            if len(result) == 2:
                break
        
        # return the majority elements
        return result

if __name__ == "__main__":
    arr = [11, 33, 33, 11, 33, 11]
    
    # Create an instance of Solution class
    sol = Solution()
    
    ans = sol.majorityElementTwo(arr)
    
    # Print the majority elements found
    print("The majority elements are:", end=" ")
    for it in ans:
        print(it, end=" ")
    print()
class Solution {
    // Function to find majority elements in an array
    majorityElementTwo(nums) {
        // Size of the array
        let n = nums.length;
        
        // List of answers
        let result = [];
        
        for (let i = 0; i < n; i++) {
            /* Checking if nums[i] is not 
            already part of the answer */
            if (result.length === 0 || result[0] !== nums[i]) {
                let cnt = 0;
                for (let j = 0; j < n; j++) {
                    // counting the frequency of nums[i]
                    if (nums[j] === nums[i]) {
                        cnt++;
                    }
                }
                
                // check if frequency is greater than n/3
                if (cnt > Math.floor(n / 3)) {
                    result.push(nums[i]);
                }
            }
            
            // if result size is equal to 2 break out of loop
            if (result.length === 2) {
                break;
            }
        }
        
        // return the majority elements
        return result;
    }
}

let arr = [11, 33, 33, 11, 33, 11];

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.majorityElementTwo(arr);

// Print the majority elements found
console.log("The majority elements are: " + ans.join(" "));

Complexity Analysis

Time Complexity: O(N²), where N is the size of the array. As for every element of the array the inner loop runs for N times. Space Complexity: O(1) the space used is so small that it can be considered constant.

Intuition

A better idea is to use a data structure to reduce the number of look-up operations and hence to reduce the time complexity. Moreover, we have been calculating the count of the same element again and again, so reduce that also.

Approach

Use a hashmap and store the elements as pairs. (Can also use frequency array based on the size of nums). Here the key will be the element of the array and the value will be the number of times it occurs.

Traverse the whole array and update the occurrence of each element.

After that, check the map if the value for any element is greater than the floor of N/3. If yes, include it in the answer. Else, iterate forward. At any point if we find that the size of answer array is 2, break out of the loop. Finally, return the answer.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find majority elements in an array
    vector<int> majorityElementTwo(vector<int>& nums) {
        
        // size of the array
        int n = nums.size(); 
        
        // list of answers
        vector<int> result; 
        
        // declaring a map
        unordered_map<int, int> mpp;
        
        // least occurrence of the majority element
        int mini = int(n / 3) + 1;
        
        // storing the elements with its occurrence
        for (int i = 0; i < n; i++) {
            mpp[nums[i]]++;
            
            // checking if nums[i] is the majority element
            if (mpp[nums[i]] == mini) {
                result.push_back(nums[i]);
            }
            
            // if result size is equal to 2 break out of loop
            if (result.size() == 2) {
                break;
            }
        }
        
        // return the majority elements
        return result;
    }
};

int main() {
    vector<int> arr = {11, 33, 33, 11, 33, 11};
    
    // Create an instance of Solution class
    Solution sol;
    
    vector<int> ans = sol.majorityElementTwo(arr);
    
    // Print the majority elements found
    cout << "The majority elements are: ";
    for (auto it : ans) {
        cout << it << " ";
    }
    cout << "\n";
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to find majority elements in an array
    public List<Integer> majorityElementTwo(int[] nums) {
        
        // Size of the array
        int n = nums.length;

        // List of answers
        List<Integer> result = new ArrayList<>();

        // Declaring a map
        Map<Integer, Integer> mpp = new HashMap<>();

        // Least occurrence of the majority element
        int mini = n / 3 + 1;

        // Storing the elements with its occurrence
        for (int i = 0; i < n; i++) {
            mpp.put(nums[i], mpp.getOrDefault(nums[i], 0) + 1);

            // Checking if nums[i] is the majority element
            if (mpp.get(nums[i]) == mini) {
                result.add(nums[i]);
            }

            // If result size is equal to 2 break out of loop
            if (result.size() == 2) {
                break;
            }
        }

        // Return the majority elements
        return result;
    }

    public static void main(String[] args) {
        int[] arr = {11, 33, 33, 11, 33, 11};

        // Create an instance of Solution class
        Solution sol = new Solution();

        List<Integer> ans = sol.majorityElementTwo(arr);

        // Print the majority elements found
        System.out.print("The majority elements are: ");
        for (int it : ans) {
            System.out.print(it + " ");
        }
        System.out.println();
    }
}
from collections import defaultdict
from typing import List

class Solution:
    # Function to find majority elements in an array
    def majorityElementTwo(self, nums: List[int]) -> List[int]:
        # Size of the array
        n = len(nums)

        # List of answers
        result = []

        # Declaring a map
        mpp = defaultdict(int)

        # Least occurrence of the majority element
        mini = n // 3 + 1

        # Storing the elements with its occurrence
        for num in nums:
            mpp[num] += 1

            # Checking if num is the majority element
            if mpp[num] == mini:
                result.append(num)

            # If result size is equal to 2 break out of loop
            if len(result) == 2:
                break

        # Return the majority elements
        return result

if __name__ == "__main__":
    arr = [11, 33, 33, 11, 33, 11]
    
    # Create an instance of Solution class
    sol = Solution()
    
    ans = sol.majorityElementTwo(arr)
    
    # Print the majority elements found
    print("The majority elements are:", *ans)

class Solution {
    // Function to find majority elements in an array
    majorityElementTwo(nums) {
        
        // Size of the array
        let n = nums.length;

        // List of answers
        let result = [];

        // Declaring a map
        let mpp = new Map();

        // Least occurrence of the majority element
        let mini = Math.floor(n / 3) + 1;

        // Storing the elements with its occurrence
        for (let i = 0; i < n; i++) {
            let num = nums[i];
            if (!mpp.has(num)) {
                mpp.set(num, 0);
            }
            mpp.set(num, mpp.get(num) + 1);

            // Checking if num is the majority element
            if (mpp.get(num) === mini) {
                result.push(num);
            }

            // If result size is equal to 2 break out of loop
            if (result.length === 2) {
                break;
            }
        }

        // Return the majority elements
        return result;
    }
}

let arr = [11, 33, 33, 11, 33, 11];

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.majorityElementTwo(arr);

// Print the majority elements found
console.log("The majority elements are:", ans.join(" "));

Complexity Analysis

Time Complexity: O(N * logN), where N is size of the given array. For using a map data structure, where insertion in the map takes logN time. And we are doing it for N elements. So, it results in the first term O(N*logN). On using unordered_map instead, the first term will be O(N) for the best and average case and for the worst case, it will be O(N²).

Space Complexity: O(N) for uing a map data structure. A list that stores a maximum of 2 elements is also used, but that space used is so small that it can be considered constant.

Intuition

Imagine you're in charge of a small party with 30 guests. Each guest has a favorite fruit, and you want to find out which fruits are most popular. Specifically, you want to know if any fruit is liked by more than a third of the guests (so more than 10 people).

As guests arrive, note their favorite fruit. Keep track of up to two different fruits at a time and how many people like each of these fruits. If a new guest likes one of the fruits you're tracking, increase the count for that fruit. If they like a different fruit and you have room to track another, you start tracking that fruit. If both tracking slots are full and the new fruit is different, you reduce the count for both tracked fruits. After all guests have arrived, you have two potential popular fruits. To confirm, go through the list one more time and count how many guests like each of these fruits.

Approach

Initialize 4 variables: cnt1 & cnt2 for tracking the counts of elements and el1 & el2 for storing the majority of elements.

Traverse through the given array. If cnt1 is 0 and the current element is not el2 then store the current element of the array as el1 along with increasing the cnt1 value by 1.

If cnt2 is 0 and the current element is not el1 then store the current element of the array as el2 along with increasing the cnt2 value by 1.

If the current element and el1 are the same increase the cnt1 by 1 and if the current element and el2 are the same increase the cnt2 by 1.

Other than all the above cases decrease cnt1 and cnt2 by 1. The integers present in el1 & el2 should be the result we are expecting. So, using another loop, to manually check their counts if they are greater than the floor(N/3).

Dry Run

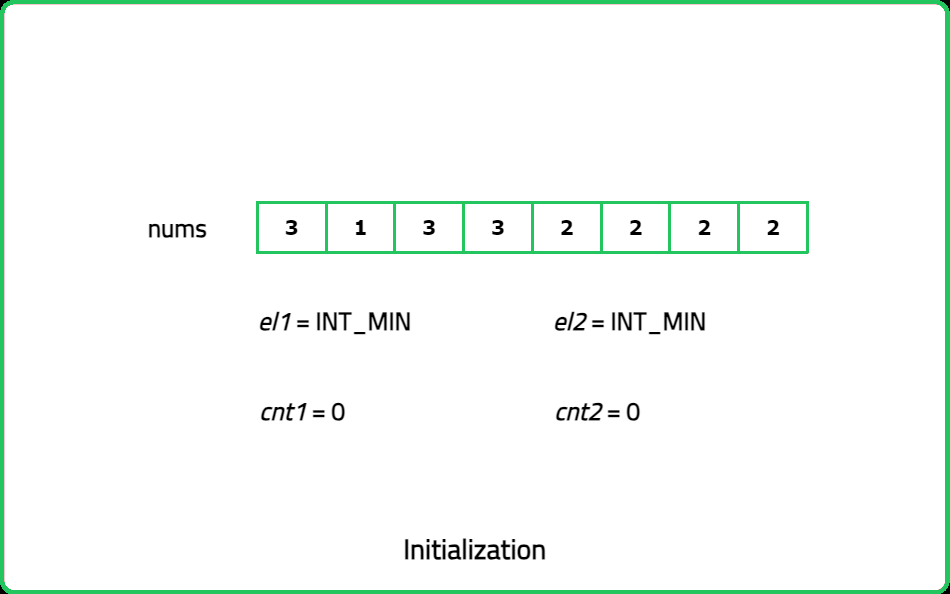
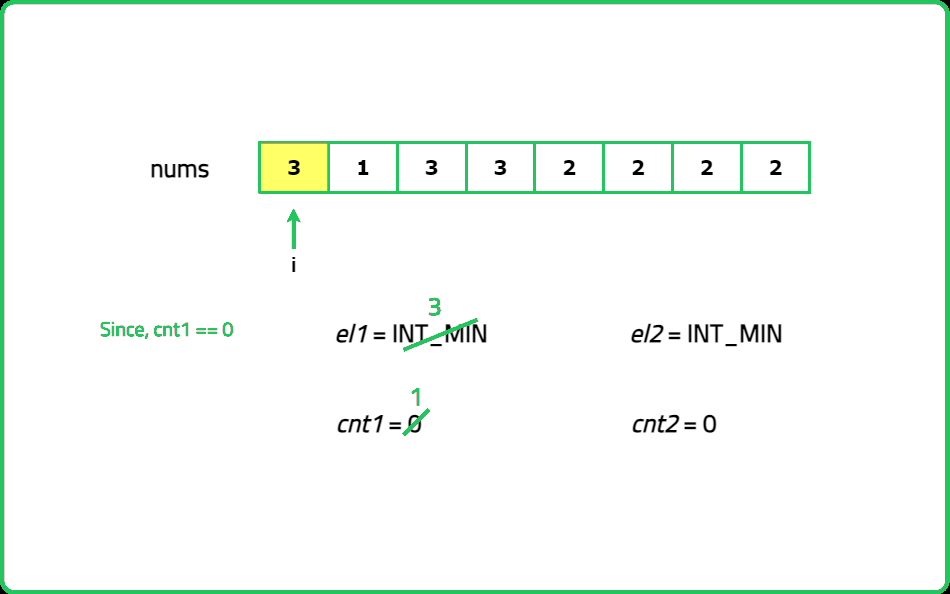
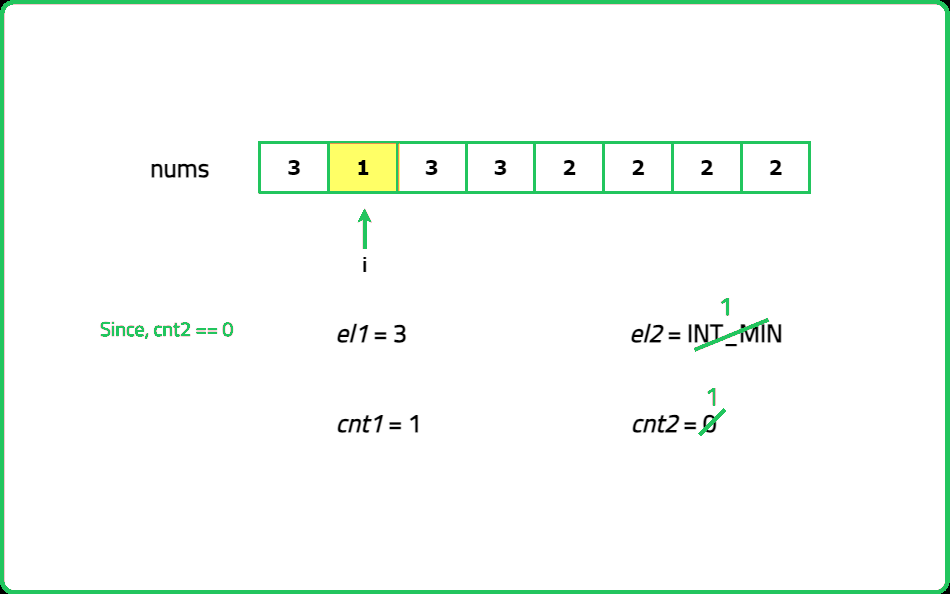
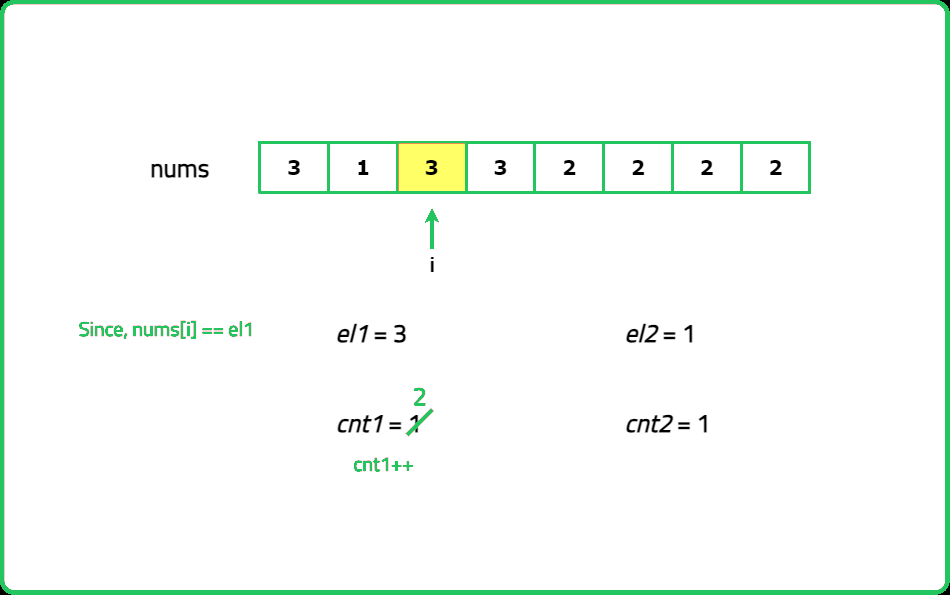
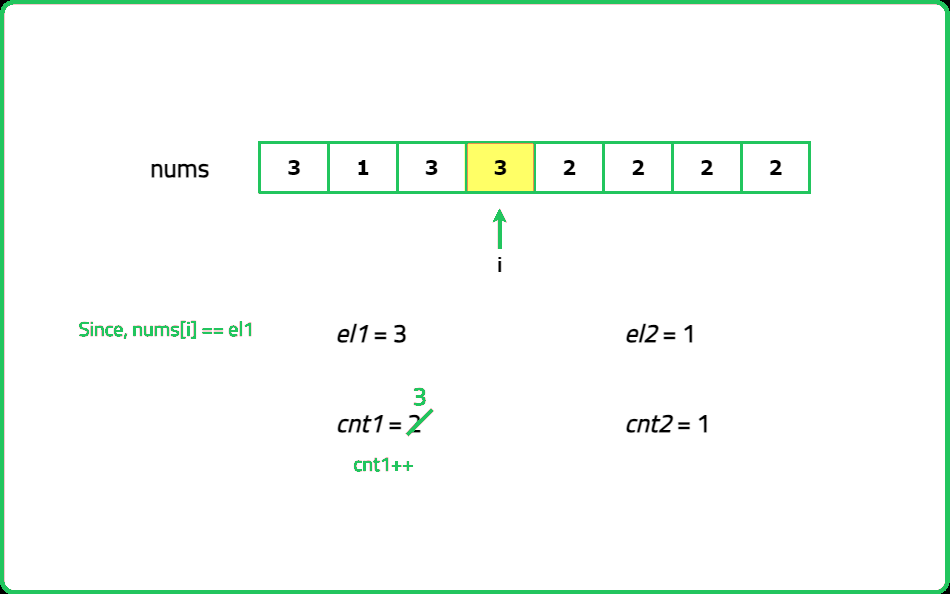
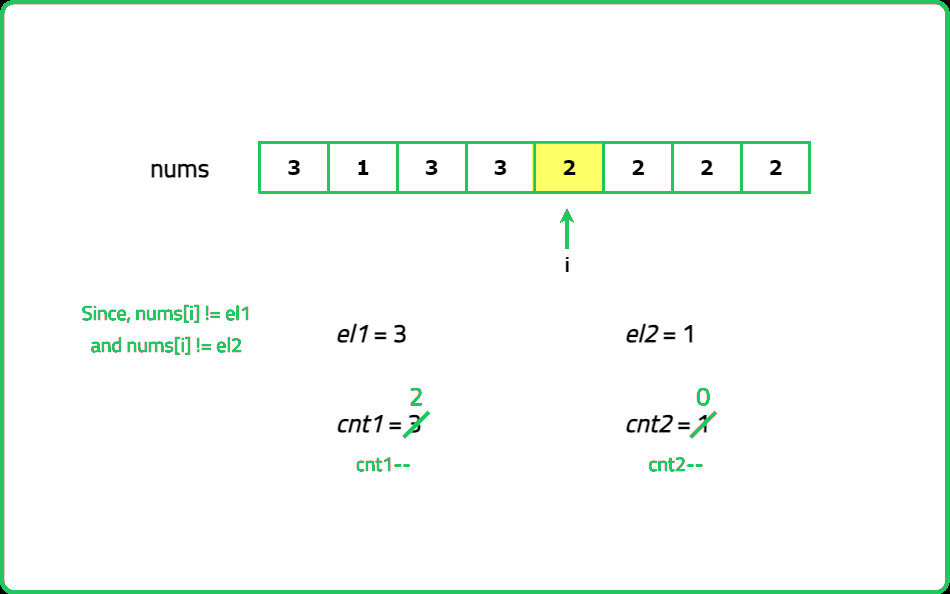
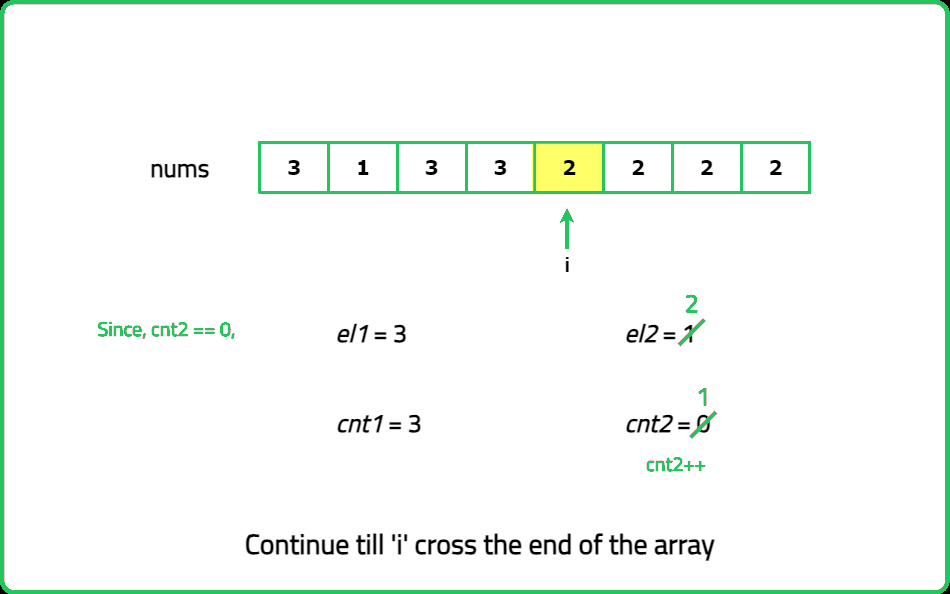
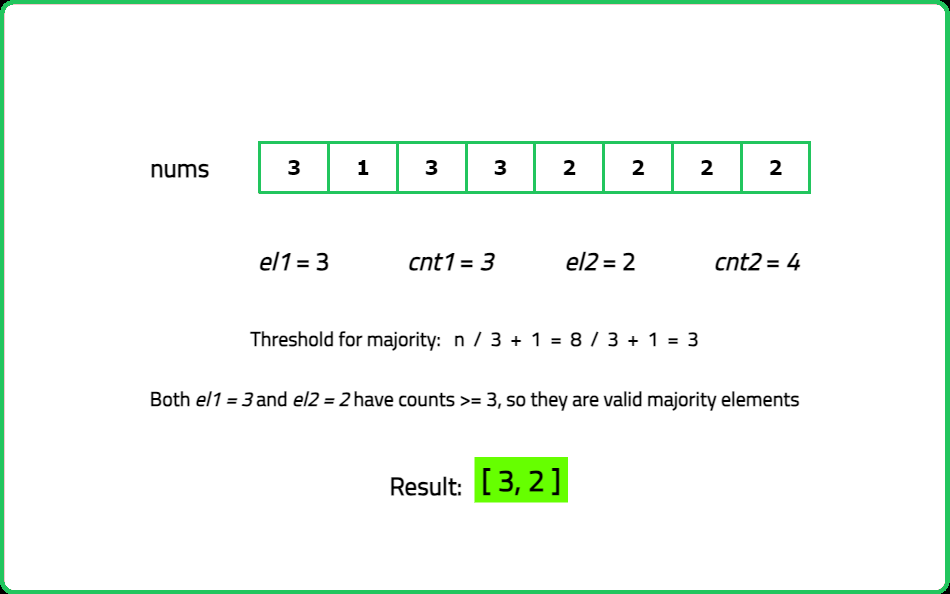
#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find majority elements in an array
    vector<int> majorityElementTwo(vector<int>& nums) {
        
        // Size of the array
        int n = nums.size(); 

        // Counts for elements el1 and el2
        int cnt1 = 0, cnt2 = 0;
        
        /*Initialize Element 1 and 
        Element 2 with INT_MIN value*/
        int el1 = INT_MIN, el2 = INT_MIN;

        /*Find the potential candidates using
        Boyer Moore's Voting Algorithm*/
        for (int i = 0; i < n; i++) {
            
            if (cnt1 == 0 && el2 != nums[i]) {
                cnt1 = 1;
                // Initialize el1 as nums[i]
                el1 = nums[i]; 
            }
            else if (cnt2 == 0 && el1 != nums[i]) {
                cnt2 = 1;
                // Initialize el2 as nums[i]
                el2 = nums[i]; 
            } 
            else if (nums[i] == el1) {
                // Increment count for el1
                cnt1++;
            } 
            else if (nums[i] == el2) {
                // Increment count for el2
                cnt2++; 
            } 
            else {
                // Decrement count for el1
                cnt1--; 
                 // Decrement count for el2
                cnt2--;
            }
        }

        //Validate the candidates by counting occurrences in nums
        //Reset counts for el1 and el2
        cnt1 = 0, cnt2 = 0; 
        
        for (int i = 0; i < n; i++) {
            if (nums[i] == el1) {
                // Count occurrences of el1
                cnt1++; 
            }
            if (nums[i] == el2) {
                 // Count occurrences of el2
                cnt2++;
            }
        }

        /* Determine the minimum count
        required for a majority element*/
        int mini = n / 3 + 1;
        
        // List of answers
        vector<int> result; 

        /*Add elements to the result vector
        if they appear more than n/3 times*/
        if (cnt1 >= mini) {
            result.push_back(el1);
        }
        if (cnt2 >= mini && el1 != el2) {
            // Avoid adding duplicate if el1 == el2
            result.push_back(el2); 
        }

        // Uncomment the following line if you want to sort the answer array
        // sort(result.begin(), result.end()); // TC --> O(2*log2) ~ O(1);

        //return the majority elements
        return result;
    }
};

int main() {
    vector<int> arr = {11, 33, 33, 11, 33, 11};
    
    // Create an instance of Solution class
    Solution sol;
  
    vector<int> ans = sol.majorityElementTwo(arr);
    
    // Print the majority elements found
    cout << "The majority elements are: ";
    for (auto it : ans) {
        cout << it << " ";
    }
    cout << "\n";
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to find majority elements in an array
    public List<Integer> majorityElementTwo(int[] nums) {
        
        // Size of the array
        int n = nums.length;

        // Counts for elements el1 and el2
        int cnt1 = 0, cnt2 = 0;
        
        /*Initialize Element 1 and 
        Element 2 with INT_MIN value*/
        int el1 = Integer.MIN_VALUE, el2 = Integer.MIN_VALUE;

        /*Find the potential candidates using
        Boyer Moore's Voting Algorithm*/
        for (int i = 0; i < n; i++) {
            if (cnt1 == 0 && el2 != nums[i]) {
                cnt1 = 1;
                // Initialize el1 as nums[i]
                el1 = nums[i]; 
            } else if (cnt2 == 0 && el1 != nums[i]) {
                cnt2 = 1;
                // Initialize el2 as nums[i]
                el2 = nums[i]; 
            } else if (nums[i] == el1) {
                // Increment count for el1
                cnt1++;
            } else if (nums[i] == el2) {
                // Increment count for el2
                cnt2++; 
            } else {
                // Decrement count for el1
                cnt1--; 
                 // Decrement count for el2
                cnt2--;
            }
        }

        //Validate the candidates by counting occurrences in nums:
        //Reset counts for el1 and el2
        cnt1 = 0; cnt2 = 0; 
        
        for (int i = 0; i < n; i++) {
            if (nums[i] == el1) {
                // Count occurrences of el1
                cnt1++; 
            }
            if (nums[i] == el2) {
                 // Count occurrences of el2
                cnt2++;
            }
        }

        /* Determine the minimum count
        required for a majority element*/
        int mini = n / 3 + 1;
        
        // List of answers
        List<Integer> result = new ArrayList<>(); 

        /*Add elements to the result vector
        if they appear more than n/3 times*/
        if (cnt1 >= mini) {
            result.add(el1);
        }
        if (cnt2 >= mini && el1 != el2) {
            // Avoid adding duplicate if el1 == el2
            result.add(el2); 
        }

        // Uncomment the following line if you want to sort the answer array 
        // Collections.sort(result); // TC --> O(2*log2) ~ O(1);

       //return the majority elements
        return result;
    }

    public static void main(String[] args) {
        int[] arr = {11, 33, 33, 11, 33, 11};
        
        // Create an instance of Solution class
        Solution sol = new Solution();
  
        List<Integer> ans = sol.majorityElementTwo(arr);
        
        // Print the majority elements found
        System.out.print("The majority elements are: ");
        for (int it : ans) {
            System.out.print(it + " ");
        }
        System.out.println();
    }
}
from typing import List

class Solution:
    # Function to find majority elements in an array
    def majorityElementTwo(self, nums: List[int]) -> List[int]:
        
        # Size of the array
        n = len(nums)

        # Counts for elements el1 and el2
        cnt1, cnt2 = 0, 0
        
        """Initialize Element 1 and 
        Element 2 with INT_MIN value"""
        el1, el2 = float('-inf'), float('-inf')

        """Find the potential candidates using
        Boyer Moore's Voting Algorithm"""
        for num in nums:
            if cnt1 == 0 and el2 != num:
                cnt1 = 1
                # Initialize el1 as num
                el1 = num 
            elif cnt2 == 0 and el1 != num:
                cnt2 = 1
                # Initialize el2 as num
                el2 = num 
            elif num == el1:
                # Increment count for el1
                cnt1 += 1
            elif num == el2:
                # Increment count for el2
                cnt2 += 1 
            else:
                # Decrement count for el1
                cnt1 -= 1 
                 # Decrement count for el2
                cnt2 -= 1

        #Validate the candidates by counting occurrences in nums
        #Reset counts for el1 and el2
        cnt1, cnt2 = 0, 0 
        
        for num in nums:
            if num == el1:
                # Count occurrences of el1
                cnt1 += 1 
            if num == el2:
                 # Count occurrences of el2
                cnt2 += 1

        """ Determine the minimum count
        required for a majority element"""
        mini = n // 3 + 1
        
        # List of answers
        result = []

        """Add elements to the result list
        if they appear more than n/3 times"""
        if cnt1 >= mini:
            result.append(el1)
            
        if cnt2 >= mini and el1 != el2:
            # Avoid adding duplicate if el1 == el2
            result.append(el2)

        # Uncomment the following line if you want to sort the answer list
        # result.sort() # TC --> O(2*log2) ~ O(1);

        #return the majority elements
        return result

if __name__ == "__main__":
    arr = [11, 33, 33, 11, 33, 11]
    
    # Create an instance of Solution class
    sol = Solution()
  
    ans = sol.majorityElementTwo(arr)
    
    # Print the majority elements found
    print("The majority elements are:", *ans)
class Solution {
    // Function to find majority elements in an array
    majorityElementTwo(nums) {
        
        // Size of the array
        let n = nums.length;

        // Counts for elements el1 and el2
        let cnt1 = 0, cnt2 = 0;
        
        /* Initialize Element 1 and 
        Element 2 with INT_MIN value */
        let el1 = Number.MIN_SAFE_INTEGER, el2 = Number.MIN_SAFE_INTEGER;

        /* Find the potential candidates using
        Boyer Moore's Voting Algorithm */
        for (let i = 0; i < n; i++) {
            if (cnt1 === 0 && el2 !== nums[i]) {
                cnt1 = 1;
                // Initialize el1 as nums[i]
                el1 = nums[i]; 
            } else if (cnt2 === 0 && el1 !== nums[i]) {
                cnt2 = 1;
                // Initialize el2 as nums[i]
                el2 = nums[i]; 
            } else if (nums[i] === el1) {
                // Increment count for el1
                cnt1++;
            } else if (nums[i] === el2) {
                // Increment count for el2
                cnt2++; 
            } else {
                // Decrement count for el1
                cnt1--; 
                // Decrement count for el2
                cnt2--;
            }
        }

        //Validate the candidates by counting occurrences in nums
        //Reset counts for el1 and el2
        cnt1 = 0; cnt2 = 0; 
        
        for (let i = 0; i < n; i++) {
            if (nums[i] === el1) {
                // Count occurrences of el1
                cnt1++; 
            }
            if (nums[i] === el2) {
                // Count occurrences of el2
                cnt2++;
            }
        }

        /* Determine the minimum count
        required for a majority element */
        let mini = Math.floor(n / 3) + 1;
        
        // List of answers
        let result = [];

        /* Add elements to the result array
        if they appear more than n/3 times */
        if (cnt1 >= mini) {
            result.push(el1);
        }
        if (cnt2 >= mini && el1 !== el2) {
            // Avoid adding duplicate if el1 == el2
            result.push(el2); 
        }

        // Uncomment the following line if you want to sort the answer array
        // result.sort((a, b) => a - b); // TC --> O(2*log2) ~ O(1);

        //return the majority elements
        return result;
    }
}

// Main function to test the solution
let arr = [11, 33, 33, 11, 33, 11];

//Create an instance of Solution class
let sol = new Solution();

let ans = sol.majorityElementTwo(arr);

// Print the majority elements found
console.log("The majority elements are:", ...ans);

Complexity Analysis

Time Complexity: O(N) + O(N), where N is size of the given array. The first O(N) is to calculate the counts and find the expected majority elements. The second one is to check if the calculated elements are the majority ones or not.

Space Complexity: O(1) for only using a list that stores a maximum of 2 elements. The space used is so small that it can be considered constant.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Can there be more than 2 majority elements ? Let's understand the scenario!

Approach

Complexity Analysis

Intuition

Approach

Complexity Analysis

Intuition

Approach

Dry Run

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code