Search in rotated sorted array-II
Binary Search
Logic Building
Easy
Given an integer array nums, sorted in ascending order (may contain duplicate values) and a target value k. Now the array is rotated at some pivot point unknown to you. Return True if k is present and otherwise, return False.
Examples:
Input : nums = [7, 8, 1, 2, 3, 3, 3, 4, 5, 6], k = 3
Output: True
Explanation: The element 3 is present in the array. So, the answer is True.
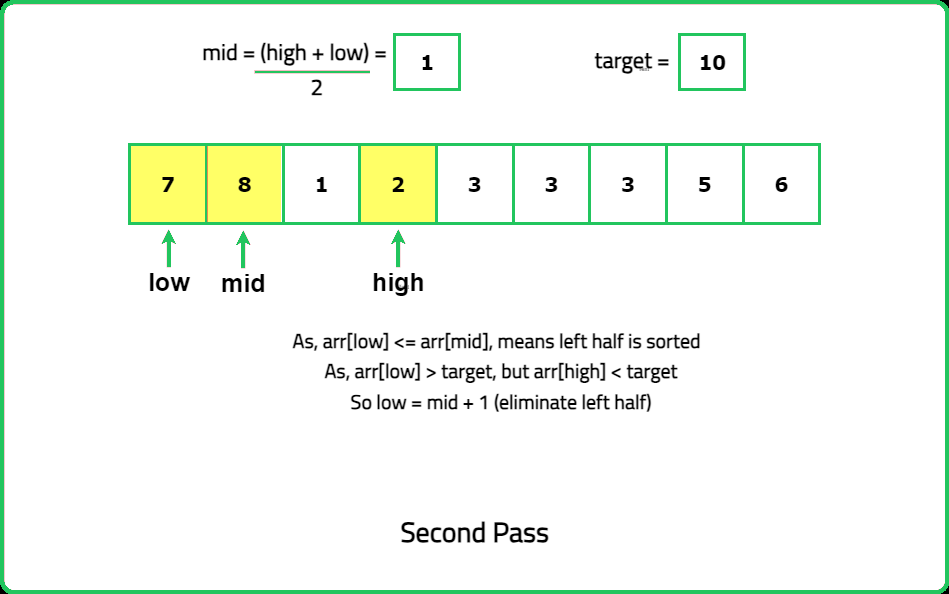
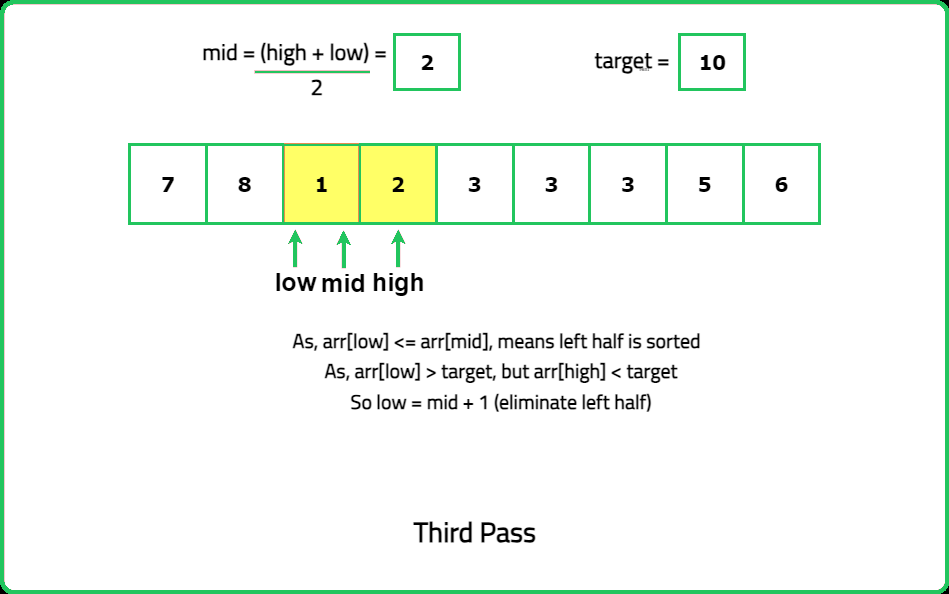
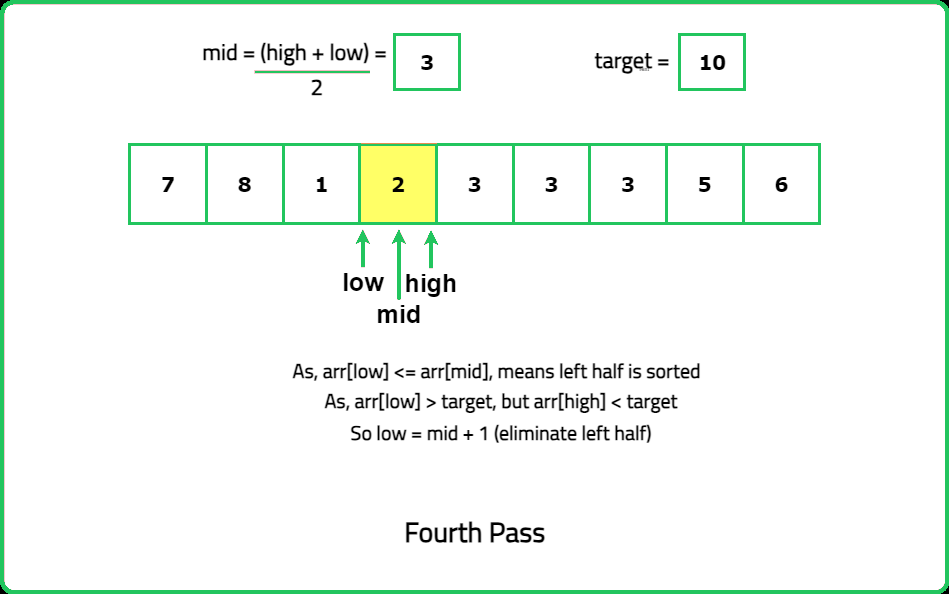
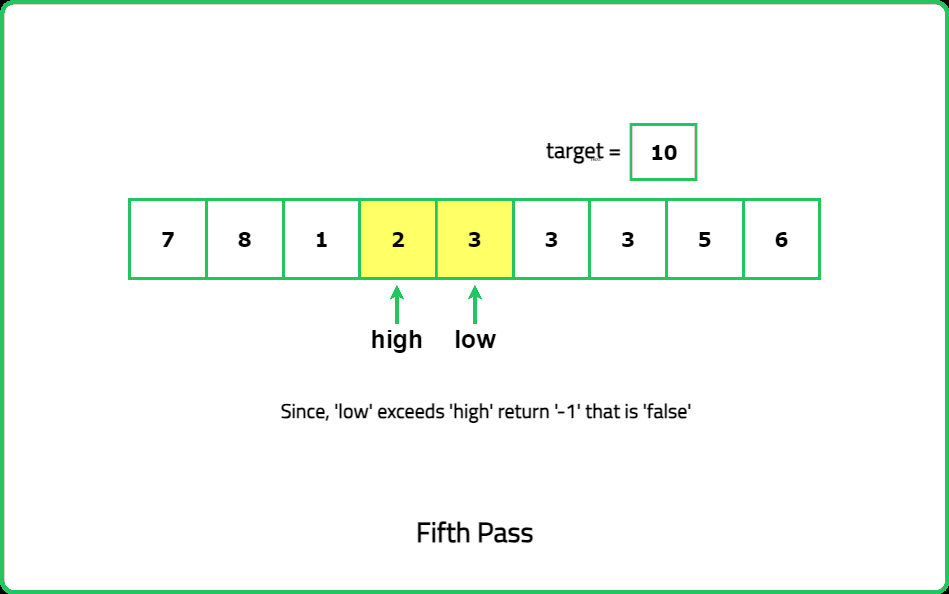
Input : nums = [7, 8, 1, 2, 3, 3, 3, 4, 5, 6], k = 10
Output: False
Explanation:The element 10 is not present in the array. So, the answer is False.
Input : nums = [7, 8, 1, 2, 3, 3, 3, 4, 5, 6], k = 7
Constraints
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums is guaranteed to be rotated at some pivot.
- -104 <= k <= 104
Hints
- In a rotated sorted array, at least one of the two halves is guaranteed to be sorted. Identify this sorted half by comparing nums[mid] with nums[low] and nums[high]. Use this information to decide where the target might lie and narrow down the search space.
- Duplicates complicate determining the sorted half. When nums[low] == nums[mid] == nums[high], you cannot deduce which half is sorted. In this case, increment low or decrement high to skip duplicates and continue the binary search.
Company Tags
Robinhood
Twilio
Walmart
Wayfair
Unity Technologies
Intel
Mastercard
Bain & Company
HashiCorp
Nutanix
Goldman Sachs
Qualcomm
Epic Systems
Stripe
Etsy
McKinsey & Company
Databricks
ARM
HCL Technologies
Freshworks
MongoDB
Byju's
Riot Games
NVIDIA
GE Healthcare
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro