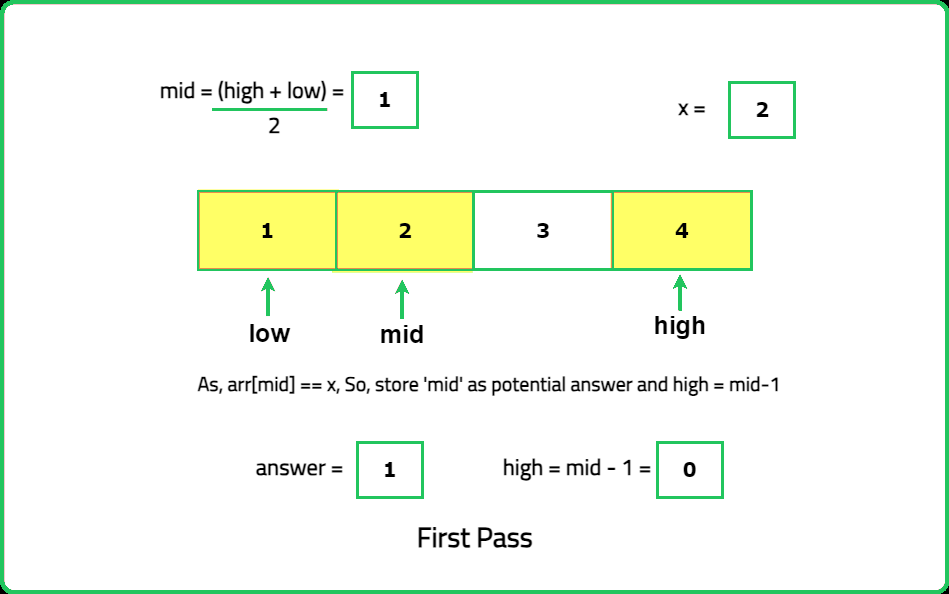
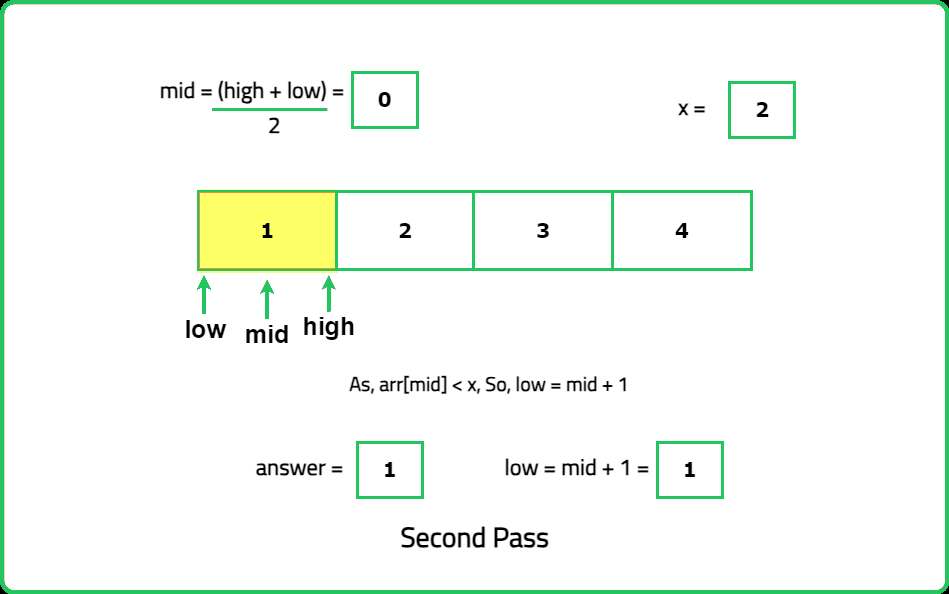
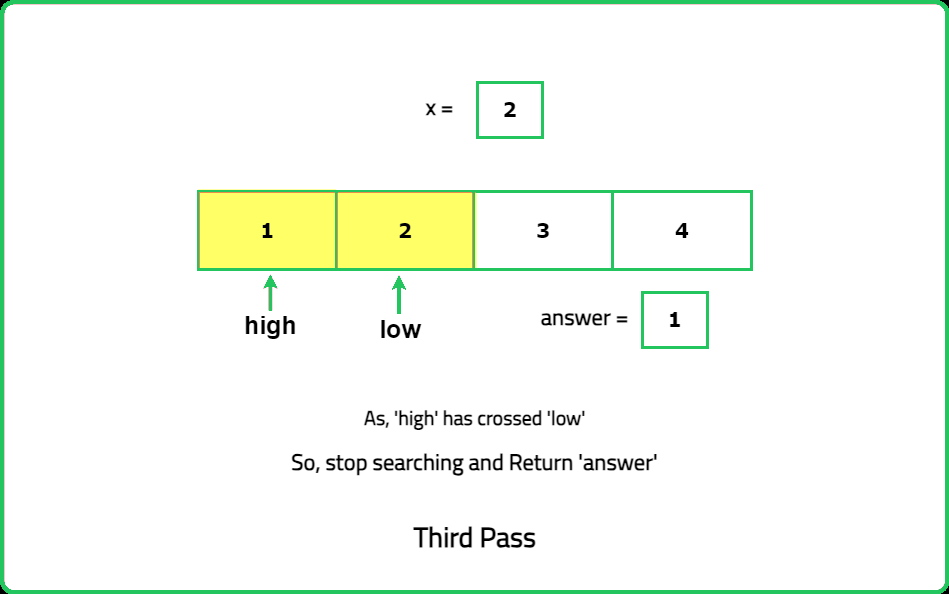
Search insert position
Binary Search
Logic Building
Easy
Given a sorted array of nums consisting of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
Examples:
Input: nums = [1, 3, 5, 6], target = 5
Output: 2
Explanation: The target value 5 is found at index 2 in the sorted array. Hence, the function returns 2.
Input: nums = [1, 3, 5, 6], target = 2
Output: 1
Explanation: The target value 2 is not found in the array. However, it should be inserted at index 1 to maintain the sorted order of the array.
Input: nums = [1, 3, 5, 6], target = 7
Constraints
- 1 <= nums.length <= 105
- -105 <= nums[i] <= 105
- nums contains distinct values sorted in ascending order.
- -105<= target <= 105
Hints
- Use the binary search algorithm to narrow down the position of the target or where it should be inserted.
- "If the target is smaller than all elements, return 0 (insert at the beginning). If the target is larger than all elements, return the size of the array (insert at the end)."
Company Tags
Oracle
Morgan Stanley
IBM
Shopify
Salesforce
Airbnb
Rakuten
Western Digital
Alibaba
Zoho
Byju's
OYO Rooms
Teladoc Health
Intel
Cloudflare
JPMorgan Chase
Square
Roche
Riot Games
Etsy
MongoDB
Stripe
Robinhood
Optum
Splunk
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro