Single Number - III
Bit Manipulation
Problems
Medium
- This type of problem, where you need to find single or unique entities in a large dataset, is related to data analytics and digital forensics
- In data analytics, unique entities are of interest because they can indicate anomalies or specific trends
- For example, in network traffic analysis, if all IP addresses are supposed to appear twice (incoming and outgoing traffic), but two appear only once, this could signify potential security issues
- In digital forensics, finding unique entities can help identify suspicious activities
- Particularly, this type of problem can be solved using XOR operation in bit manipulation, a valuable technique in many areas of software, including cryptography and error detection/correction codes
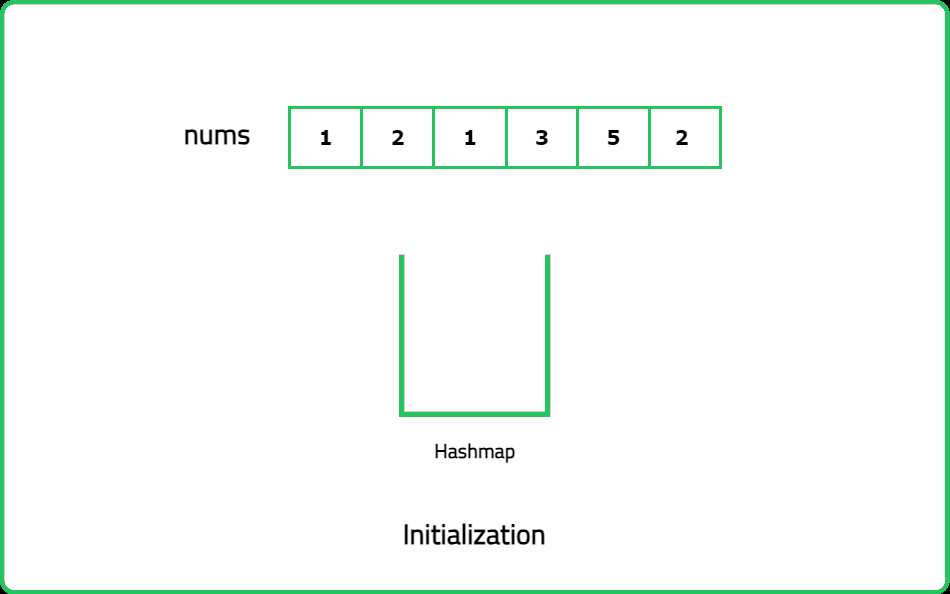
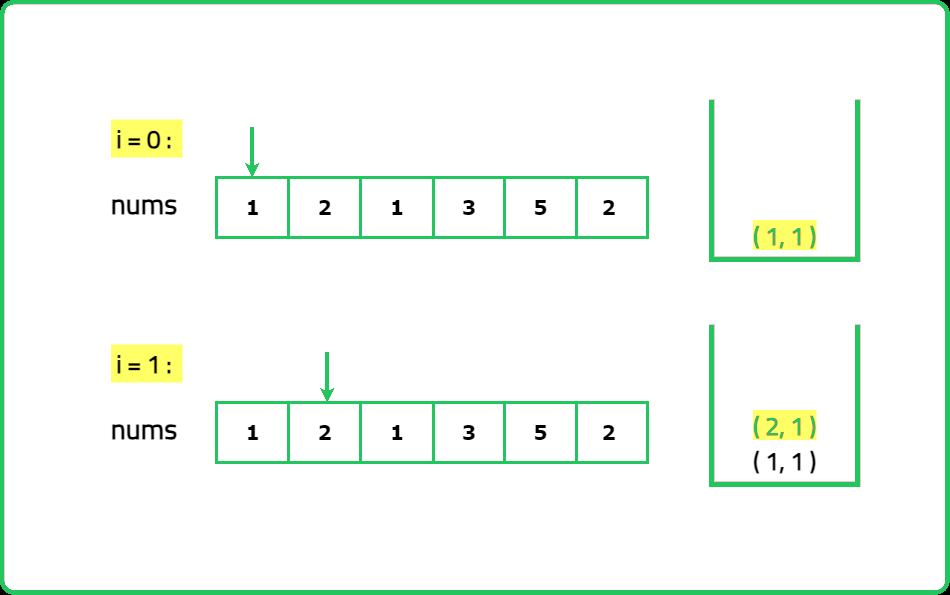
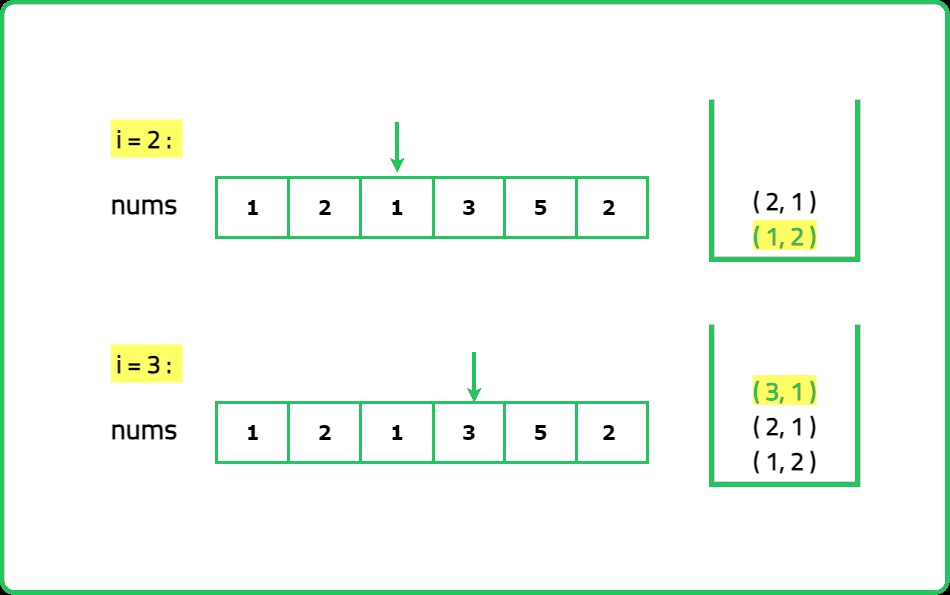
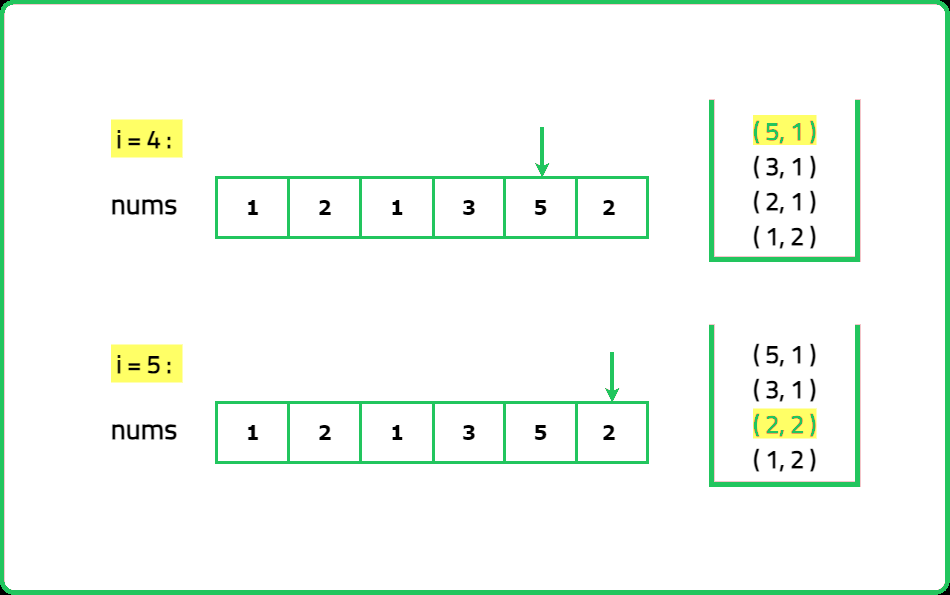
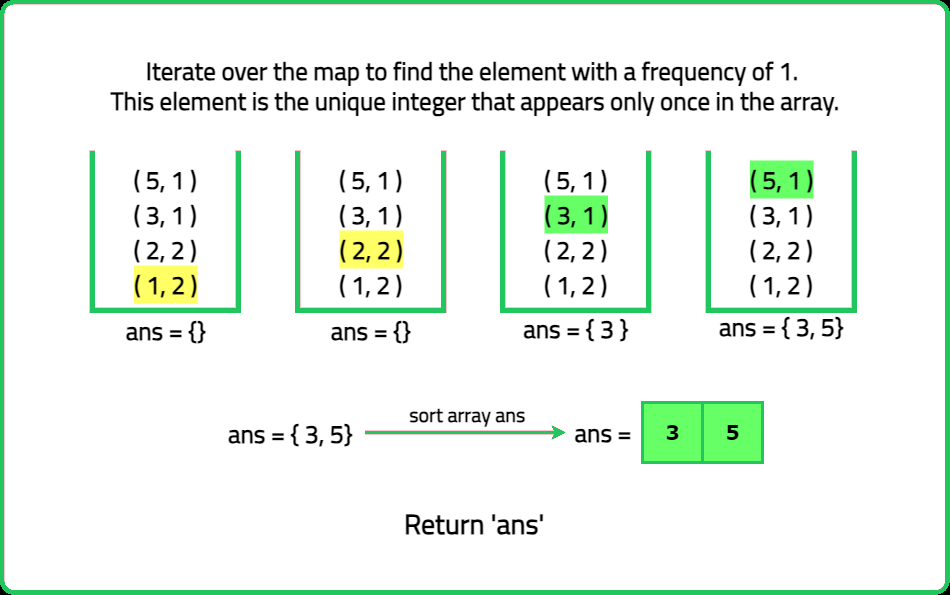
Given an array nums of length n, every integer in the array appears twice except for two integers. Identify and return the two integers that appear only once in the array. Return the two numbers in ascending order.
For example, if nums = [1, 2, 1, 3, 5, 2], the correct answer is [3, 5], not [5, 3].
Examples:
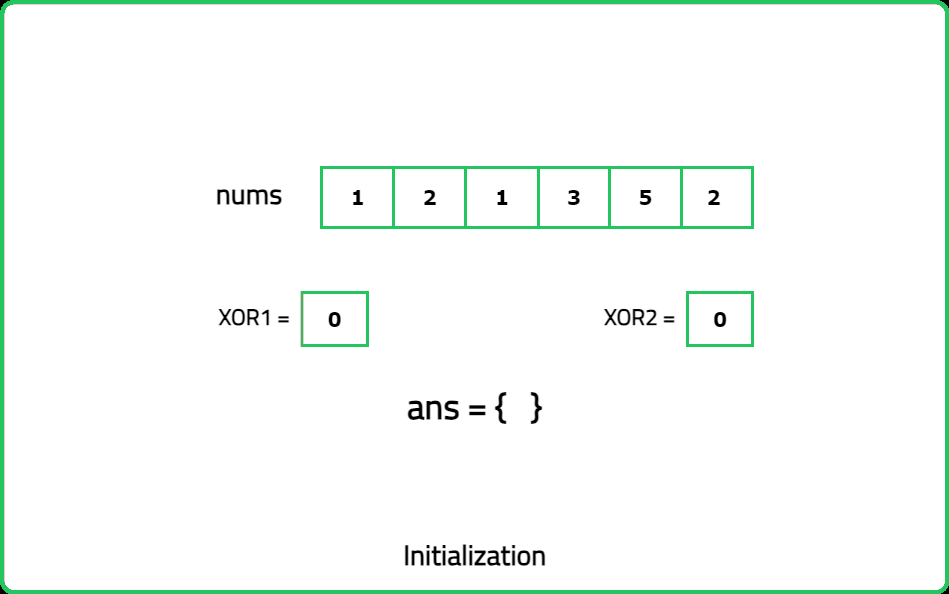
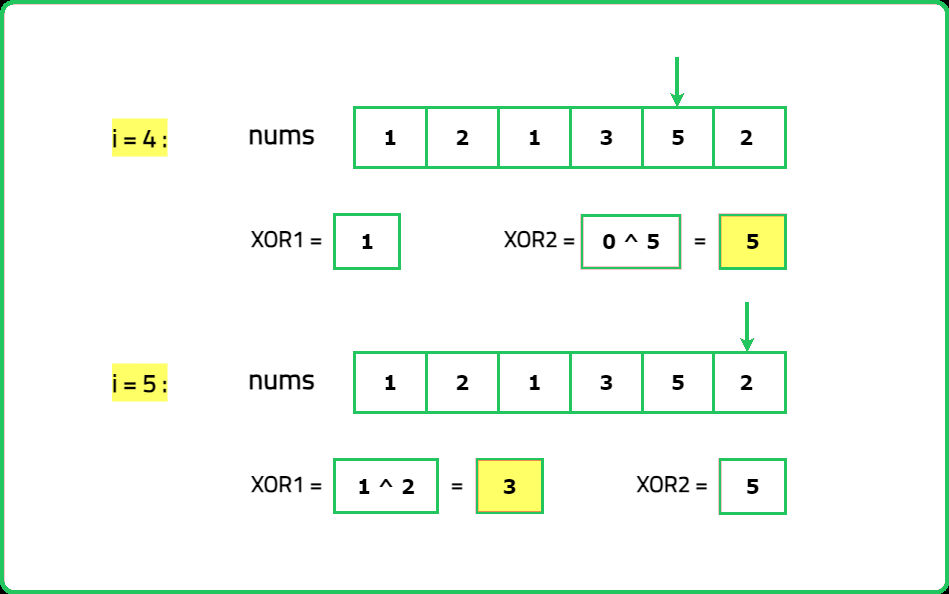
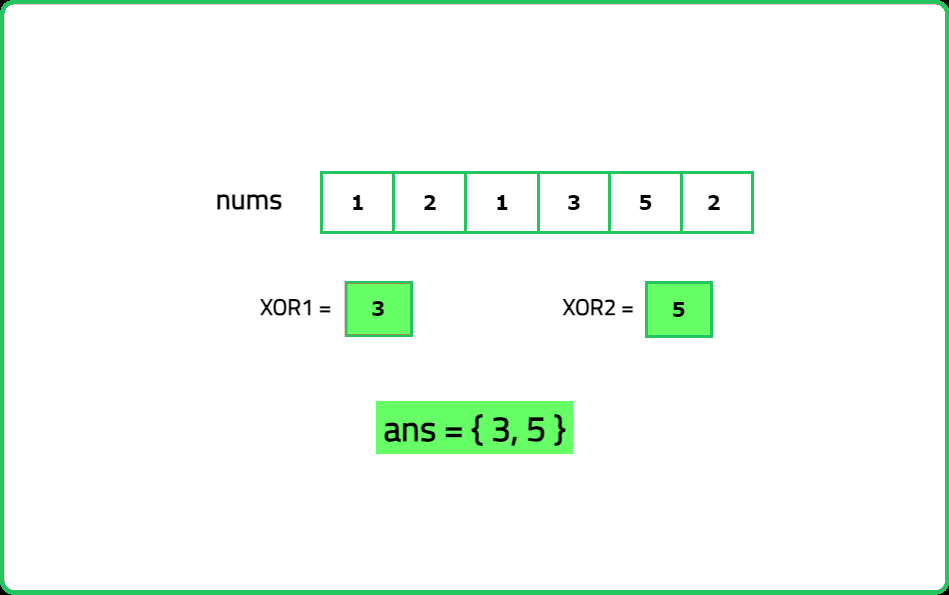
Input : nums = [1, 2, 1, 3, 5, 2]
Output : [3, 5]
Explanation : The integers 3 and 5 have appeared only once.
Input : nums = [-1, 0]
Output : [-1, 0]
Explanation : The integers -1 and 0 have appeared only once.
Input : nums = [1, 9, 1, 2, 8, 2]
Constraints
- 2 <= nums.length <= 105
- -3*105 <= nums[i] <= 3*105
- Every integer in nums appears twice except two integers.
Hints
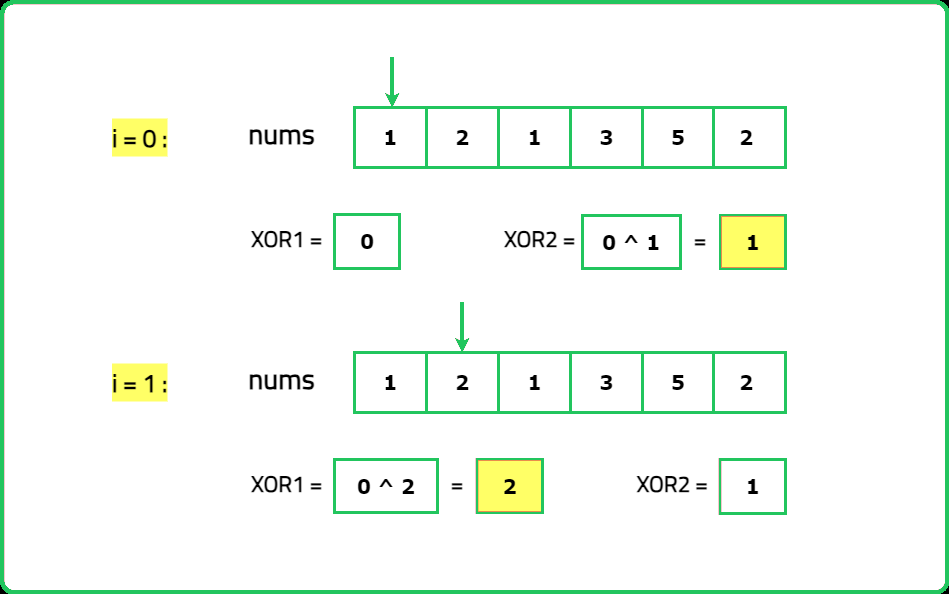
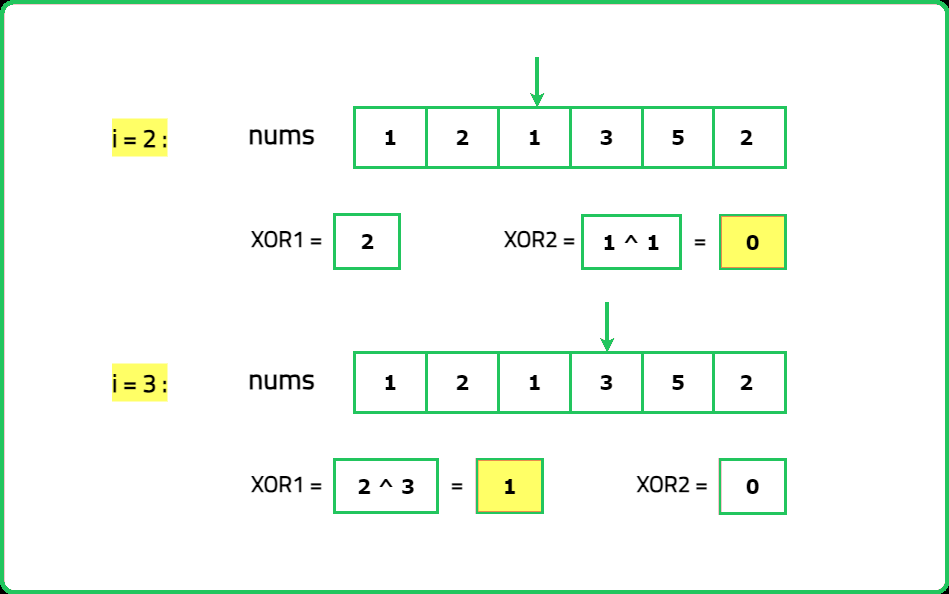
- The XOR result, x⊕y, will have at least one bit set to 1. This bit represents a position where x and y differ. Isolate this bit by using diff=xor_result&−xor_result, which gives the rightmost set bit.
- Partition the array into two groups based on whether the numbers have the differentiating bit set (1) or unset (0). One group will contain x, and the other will contain y. XOR the elements in each group to isolate x and y.
Company Tags
Seagate Technology
Zoho
Qualcomm
Byju's
Micron Technology
Roche
Walmart
HCL Technologies
Databricks
Bloomberg
Shopify
Airbnb
MongoDB
JPMorgan Chase
Twilio
Freshworks
Square
OYO Rooms
Boston Consulting Group
Dropbox
Morgan Stanley
KPMG
Visa
Lyft
NVIDIA
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe