M Coloring Problem

Real-Life Problem Solving

Consider a scenario where several tasks need to be scheduled, each task requiring a specific resource. The objective is to assign resources to tasks such that no two tasks requiring the same resource are scheduled simultaneously. This is akin to assigning colors to nodes in a graph, where no two adjacent nodes (tasks) share the same color (resource). The challenge is to determine if it's possible to schedule all tasks using a limited number of resources.

Recursion Process Intuition

Imagine attempting to assign a color to a node in a graph, starting from the first node and moving sequentially. For each node, every possible color is tried, ensuring it does not conflict with already colored adjacent nodes. If a valid color is found, the process moves to the next node. If a conflict arises, the current assignment is undone (backtracked), and the next color is attempted. This recursive process continues until all nodes are successfully colored or all possibilities are exhausted, indicating no valid coloring exists.

Approach

Represent the graph using an adjacency list for efficient traversal and initialize a colors array to keep track of the assigned colors for each node, starting with no colors assigned.
Define a function to check if it's safe to assign a specific color to a node by ensuring no adjacent node has the same color.
Implement a recursive function to attempt to color each node:
- If all nodes are successfully colored, return true.
- For the current node, try all possible colors from 1 to m.
- Check if assigning a color is safe using the helper function.
- If safe, assign the color and recursively attempt to color the next node.
- If coloring the next node fails, reset the current node's color and try the next color.
- If no valid color is found, return false.
Start the coloring process from the first node and continue recursively until all nodes are processed. The result of the recursive function indicates whether the graph can be colored with the given number of colors.

Dry Run

Solution

#include bits/stdc++.h
using namespace std;

class Solution {
public:

    // Function to check if it's safe to color the node with a given color
    bool isSafe(int col, int node, vector<int>& colors, vector<int> adj[]) {
        // Check adjacent nodes
        for (int i = 0; i < adj[node].size(); i++) {
            // If an adjacent node has the same color
            if (colors[adj[node][i]] == col) return false;
        }
        return true; // Safe to color
    }

    // Recursive function to solve graph coloring problem
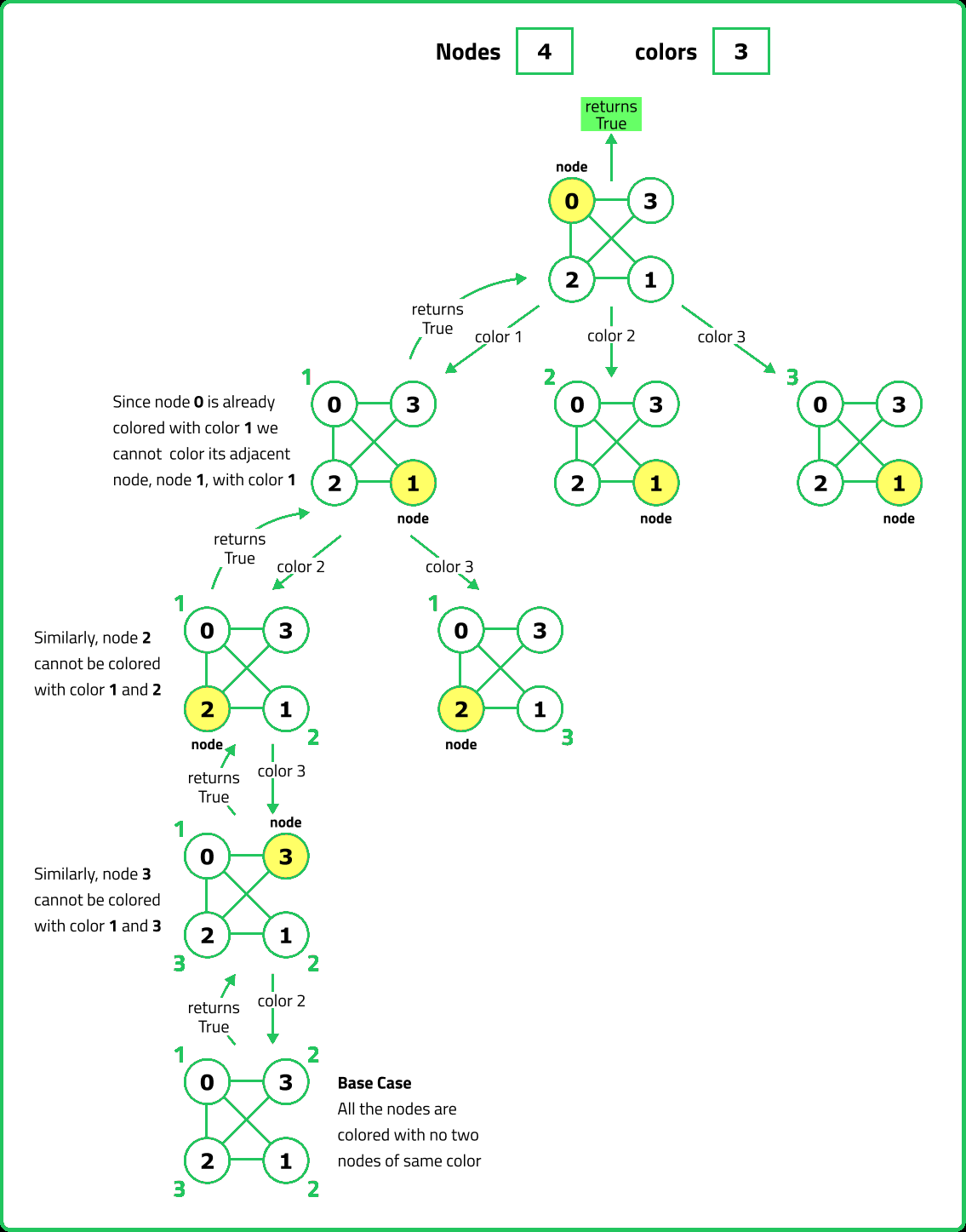
    bool solve(int node, int m, int n, vector<int>& colors, vector<int> adj[]) {
        // If all nodes are colored
        if (n == node) return true;
        // Try all colors from 1 to m
        for (int i = 1; i <= m; i++) {
            // Check if it is safe to color the node with color i
            if (isSafe(i, node, colors, adj)) {
             // Assign color i to node
                colors[node] = i;
                // Recursively try to color the next node
                if (solve(node + 1, m, n, colors, adj)) return true;
                // Reset color if it doesn't lead to a solution
                colors[node] = 0; 
            }
        }
        // No color can be assigned
        return false; 
    }

    // Function to check if the graph can be colored with m colors
    bool graphColoring(vector<vector<int>>& edges, int m, int n) {
     // Adjacency list representation of the graph 
        vector<int> adj[n];

        // Build the graph from edges
        for (int i = 0; i < edges.size(); i++) {
            adj[edges[i][0]].push_back(edges[i][1]);
            adj[edges[i][1]].push_back(edges[i][0]);
        }
        // Initialize all colors to 0 (uncolored)
        vector<int> colors(n, 0);
        // Start solving from the first node
        return solve(0, m, n, colors, adj);
    }
};

int main() {
    Solution sol;
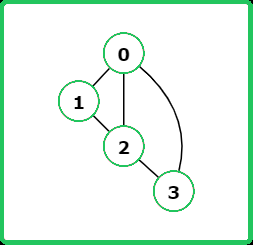
    vector<vector<int>> edges = {
        {0, 1}, {0, 2}, {1, 2}, {1, 3}
    };
    int m = 3; // Number of colors
    int n = 4; // Number of nodes

    // Check if the graph can be colored with m colors
    if (sol.graphColoring(edges, m, n)) {
        cout << "The graph can be colored with " << m << " colors." << endl;
    } else {
        cout << "The graph cannot be colored with " << m << " colors." << endl;
    }

    return 0;
}
import java.util.*;

class Solution {

    // Function to check if it's safe to color the node with a given color
    private boolean isSafe(int col, int node, int[] colors, List<List<Integer>> adj) {
        // Check adjacent nodes
        for (int neighbor : adj.get(node)) {
            // If an adjacent node has the same color
            if (colors[neighbor] == col) return false;
        }
        return true; // Safe to color
    }

    // Recursive function to solve graph coloring problem
    private boolean solve(int node, int m, int n, int[] colors, List<List<Integer>> adj) {
        // If all nodes are colored
        if (n == node) return true;
        // Try all colors from 1 to m
        for (int i = 1; i <= m; i++) {
            // Check if it is safe to color the node with color i
            if (isSafe(i, node, colors, adj)) {
                colors[node] = i; // Assign color i to node
                // Recursively try to color the next node
                if (solve(node + 1, m, n, colors, adj)) return true;
                colors[node] = 0; // Reset color if it doesn't lead to a solution
            }
        }
        return false; // No color can be assigned
    }

    // Function to check if the graph can be colored with m colors
    public boolean graphColoring(int[][] edges, int m, int n) {
        // Create adjacency list representation of the graph
        List<List<Integer>> adj = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adj.add(new ArrayList<>());
        }
        // Build the graph from edges
        for (int[] edge : edges) {
            adj.get(edge[0]).add(edge[1]);
            adj.get(edge[1]).add(edge[0]);
        }
        
        int[] colors = new int[n]; // Initialize all colors to 0 (uncolored)
        // Start solving from the first node
        return solve(0, m, n, colors, adj);
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        int[][] edges = {
            {0, 1}, {0, 2}, {1, 2}, {1, 3}
        };
        int m = 3; // Number of colors
        int n = 4; // Number of nodes

        // Check if the graph can be colored with m colors
        if (sol.graphColoring(edges, m, n)) {
            System.out.println("The graph can be colored with " + m + " colors.");
        } else {
            System.out.println("The graph cannot be colored with " + m + " colors.");
        }
    }
}
class Solution:
    def isSafe(self, col, node, colors, adj):
        # Function to check if it's safe to color the node with a given color
        # Check adjacent nodes
        for neighbor in adj[node]:
            # If an adjacent node has the same color
            if colors[neighbor] == col:
                return False
        return True # Safe to color

    def solve(self, node, m, n, colors, adj):
        # Recursive function to solve graph coloring problem
        # If all nodes are colored
        if n == node:
            return True
        # Try all colors from 1 to m
        for i in range(1, m + 1):
            # Check if it is safe to color the node with color i
            if self.isSafe(i, node, colors, adj):
                colors[node] = i # Assign color i to node
                # Recursively try to color the next node
                if self.solve(node + 1, m, n, colors, adj):
                    return True
                colors[node] = 0 # Reset color if it doesn't lead to a solution
        return False # No color can be assigned

    def graphColoring(self, edges, m, n):
        # Function to check if the graph can be colored with m colors
        adj = [[] for _ in range(n)] # Create adjacency list representation of the graph
        # Build the graph from edges
        for edge in edges:
            adj[edge[0]].append(edge[1])
            adj[edge[1]].append(edge[0])
        
        colors = [0] * n # Initialize all colors to 0 (uncolored)
        # Start solving from the first node
        return self.solve(0, m, n, colors, adj)

# Example usage
if __name__ == "__main__":
    sol = Solution()
    edges = [
        [0, 1], [0, 2], [1, 2], [1, 3]
    ]
    m = 3 # Number of colors
    n = 4 # Number of nodes

    # Check if the graph can be colored with m colors
    if sol.graphColoring(edges, m, n):
        print("The graph can be colored with", m, "colors.")
    else:
        print("The graph cannot be colored with", m, "colors.")
class Solution {
    // Function to check if it's safe to color the node with a given color
    isSafe(col, node, colors, adj) {
        // Check adjacent nodes
        for (let neighbor of adj[node]) {
            // If an adjacent node has the same color
            if (colors[neighbor] === col) return false;
        }
        return true; // Safe to color
    }

    // Recursive function to solve graph coloring problem
    solve(node, m, n, colors, adj) {
        // If all nodes are colored
        if (n === node) return true;
        // Try all colors from 1 to m
        for (let i = 1; i <= m; i++) {
            // Check if it is safe to color the node with color i
            if (this.isSafe(i, node, colors, adj)) {
                colors[node] = i; // Assign color i to node
                // Recursively try to color the next node
                if (this.solve(node + 1, m, n, colors, adj)) return true;
                colors[node] = 0; // Reset color if it doesn't lead to a solution
            }
        }
        return false; // No color can be assigned
    }

    // Function to check if the graph can be colored with m colors
    graphColoring(edges, m, n) {
        // Create adjacency list representation of the graph
        let adj = Array.from({ length: n }, () => []);
        // Build the graph from edges
        for (let edge of edges) {
            adj[edge[0]].push(edge[1]);
            adj[edge[1]].push(edge[0]);
        }

        let colors = new Array(n).fill(0); // Initialize all colors to 0 (uncolored)
        // Start solving from the first node
        return this.solve(0, m, n, colors, adj);
    }
}

// Example usage
const sol = new Solution();
const edges = [
    [0, 1], [0, 2], [1, 2], [1, 3]
];
const m = 3; // Number of colors
const n = 4; // Number of nodes

// Check if the graph can be colored with m colors
if (sol.graphColoring(edges, m, n)) {
    console.log("The graph can be colored with " + m + " colors.");
} else {
    console.log("The graph cannot be colored with " + m + " colors.");
}

Complexity Analysis

Time Complexity : O(M^N) where m is the number of colors and n is the number of nodes, since each node can be colored in m ways and there are n nodes to color.

Space Complexity : O(N) for the colors array and O(n) for the adjacency list, resulting in O(N) total space complexity.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Real-Life Problem Solving

Recursion Process Intuition

Approach

Dry Run

Solution

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code