Disjoint Set
Graphs
Minimum Spanning Tree
Hard
- Fun Fact: The union-find data structure, or the disjoint set, is specifically designed for efficient handling of the equivalence relation problem
- It plays a fundamental part in some very popular real-world applications
- For example, it is a key component in Kruskal's algorithm, which is a widely used algorithm to find the minimum spanning tree in a graph
- The minimum spanning tree has plenty of utilities, from designing the efficient networking in telecom industry to powering the recommendation engines in apps like Netflix, where it's used to cluster users based on their viewing patterns
- The rank and size heuristics are used to optimize the efficiency of the union-find operations, making these applications even more performant in solving real-world problems
Design a disjoint set (also called union-find) data structure that supports the following operations:
DisjointSet(int n) initializes the disjoint set with n elements.
void unionByRank(int u, int v) merges the sets containing u and v using the rank heuristic.
void unionBySize(int u, int v) merges the sets containing u and v using the size heuristic.
bool find(int u, int v) checks if the elements u and v are in the same set and returns true if they are, otherwise false.
Examples:
Input:
["DisjointSet", "unionByRank", "unionBySize", "find", "find"]
[[5], [0, 1], [2, 3], [0, 1], [0, 3]]
Output:
[null, null, null, true, false]
Explanation:
DisjointSet ds = new DisjointSet(5); // Initialize a disjoint set with 5 elements
ds.unionByRank(0, 1); // Merge sets containing 0 and 1 using rank
ds.unionBySize(2, 3); // Merge sets containing 2 and 3 using size
ds.find(0, 1); // Returns true as 0 and 1 are in the same set
ds.find(0, 3); // Returns false as 0 and 3 are not in the same set
Input:
["DisjointSet", "unionBySize", "unionBySize", "find", "find"]
[[3], [0, 1], [1, 2], [0, 2], [0, 1]]
Output:
[null, null, null, true, true]
Explanation:
DisjointSet ds = new DisjointSet(3); // Initialize a disjoint set with 3 elements
ds.unionBySize(0, 1); // Merge sets containing 0 and 1 using size
ds.unionBySize(1, 2); // Merge sets containing 1 and 2 using rank
ds.find(0, 2); // Returns true as 0 and 2 are in the same set
ds.find(0, 1); // Returns true as 0 and 1 are in the same set
Input:
["DisjointSet", "unionByRank", "unionBySize", "unionByRank", "find", "find"]
[[5], [0, 1], [3, 4], [1, 2], [0, 2], [1, 3]]
Constraints
- 1 <= n <= 104
- 0 <= u, v < n
- At most 5 * 104 calls will be made to unionByRank, unionBySize, and find
Hints
- When calling find(), update the parent pointer to the root, making future lookups O(1).
- "Attach the smaller height tree to the larger height tree to keep the structure balanced. Attach the smaller set to the larger set to keep set sizes balanced."
Company Tags
Wayfair
Alibaba
Riot Games
PayPal
Walmart
Ernst & Young
Docker
NVIDIA
Medtronic
Reddit
Siemens Healthineers
Etsy
Rakuten
Intel
Salesforce
HCL Technologies
Target
Broadcom
Databricks
Optum
Red Hat
Chewy
Electronic Arts
PwC
Splunk
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Introduction:
The Disjoint Set data structure is a crucial topic in the graph series. To understand its necessity, consider the following problem:
Problem Statement:
Given two components of an undirected graph, determine if node 1 and node 5 belong to the same component.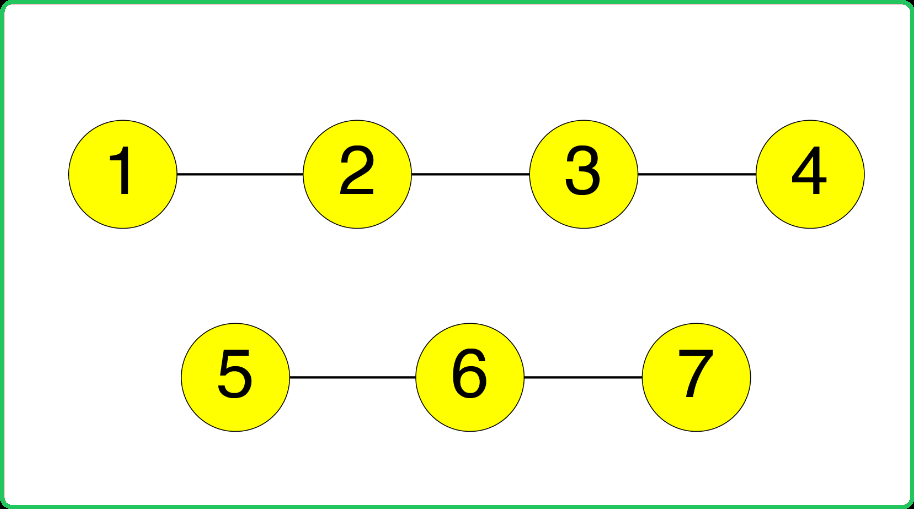
Approach:
To solve this problem, Depth-First Search (DFS) or Breadth-First Search (BFS) traversal techniques can be employed. By traversing the graph components, it is evident that node 1 and node 5 are in different components. This brute force approach has a time complexity of O(N+E) where N is the number of nodes and E is the number of edges. However, using a Disjoint Set data structure, this problem can be solved in constant time.The Disjoint Set data structure is particularly useful for dynamic graphs.
Dynamic Graph:
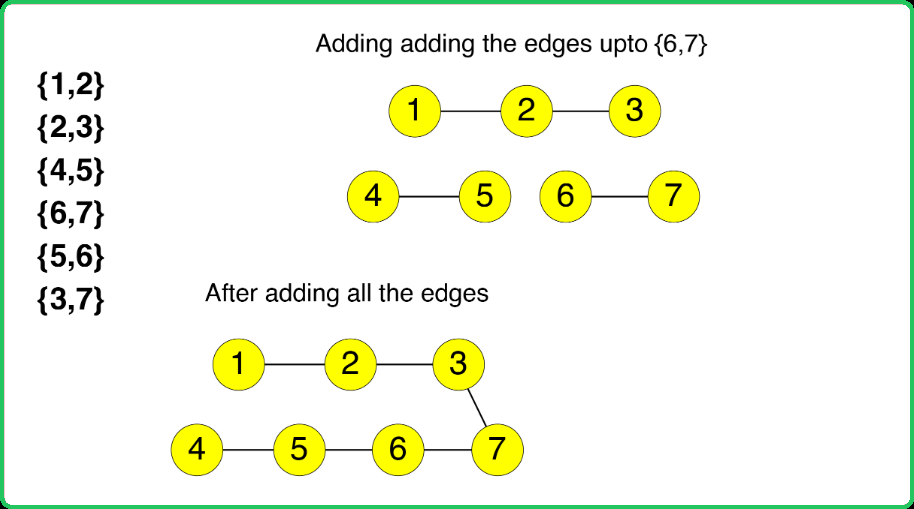
A dynamic graph refers to a graph that continuously changes its configuration.For example, consider the edge information for a graph as:
{{1,2},{2,3},{4,5},{6,7},{5,6},{3,7}} Adding edges one by one changes the structure of the graph at each step. After adding the first four edges, nodes 4 and 1 belong to different components. After adding all six edges, nodes 4 and 1 belong to the same component.
Now, to answer any query that requires checking whether two nodes belong to the same component in the graph, if the traversal techniques are used, then it will be extremely time consuming as the graph is changing every time. Here, Disjoint Set plays a crucial role. Disjoint Set can quickly determine if two arbitrary nodes u and v are in the same component at any step.
Functionalities of Disjoint Set Data Structure:
The Disjoint Set data structure provides two primary functionalities:
- Finding the parent(ultimate parent) of a particular node.
- Union operation (which adds an edge between two nodes):
- Union by Rank
- Union by Size
Terminologies:
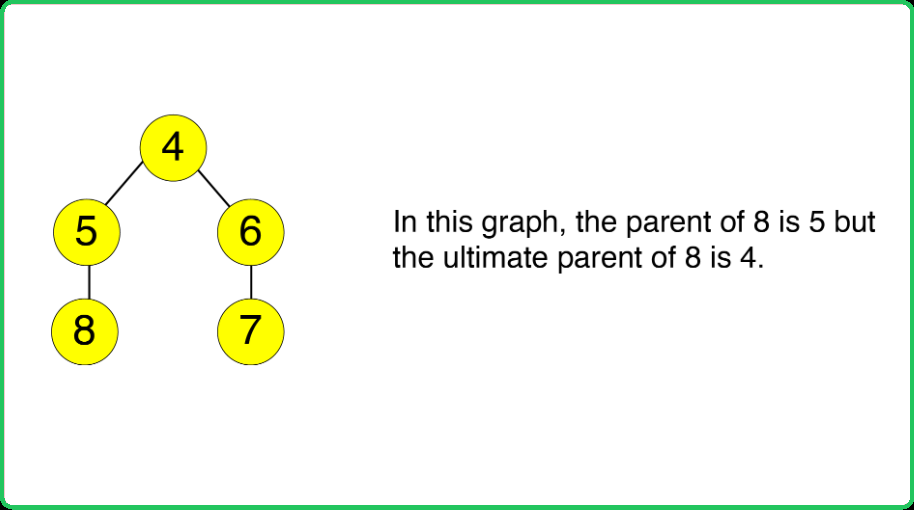
- Ultimate Parent: The parent of a node refers to the node right above that particular node. The ultimate parent refers to the topmost node or the root node of that component.
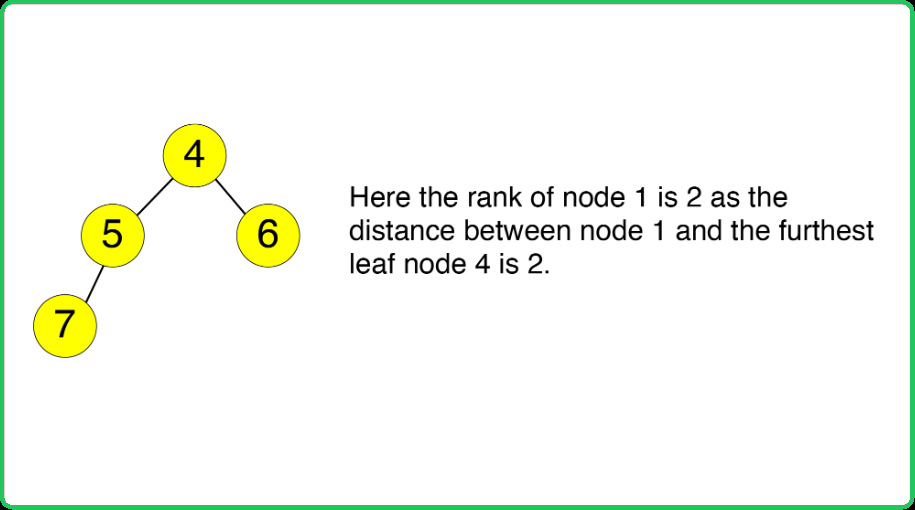
- Rank: The rank of a node refers to the distance (the number of nodes including the leaf node) between the furthest leaf node and the current node. Rank includes all nodes beneath the current node.
Implementation:
To implement Union by rank, two arrays of size N (number of nodes) are needed:
- Rank array: Storing the rank of each node.
- Parent array: Storing the ultimate parents of each node.
Algorithm:
-
Initial Configuration:
- Rank array: Initialized with zeros.
- Parent array: Initialized with the value of nodes, i.e., parent[i] = i.
-
Union Function Steps:
- The Union function requires two nodes (let's say u and v) as arguments. Find the ultimate parent of u and v using the a helper findPar() function. Let pu and pv be the ultimate parents of u and v respectively.
- Determine the rank of pu and pv.
- Connect the ultimate parent with a smaller rank to the other ultimate parent with a larger rank. If the ranks are equal, connect any parent to the other and increase the rank of the parent node to which the other is connected.
Example:
Given the edges of a graph as {{1,2},{2,3},{4,5},{6,7},{5,6}}: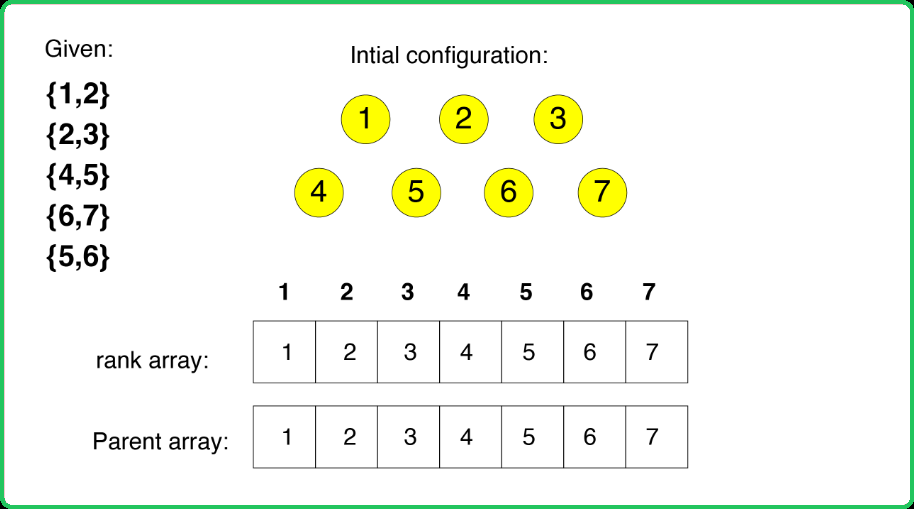
Observations:
Observation 1:
Only the ultimate parent is considered, not the immediate parent. For instance, after Union by rank operations, if nodes 5 and 7 are queried, the answer is yes. Their immediate parents differ, but their ultimate parent is the same, i.e., node 4. Thus, the ultimate parent is crucial.For this the findPar() function helps find the ultimate parent of a particular node.
findPar() Function: This function takes a single node as an argument and finds the ultimate parent for that node.
Observation 2:
Finding the ultimate parent of each query separately using recursion takes O(logN) time complexity. However, the operation is desired in constant time. This is where the path compression technique is useful.Path Compression: Connecting each node in a path to its ultimate parent reduces time complexity nearly to constant time. The path from the node to its ultimate parent is compressed to only a single edge.
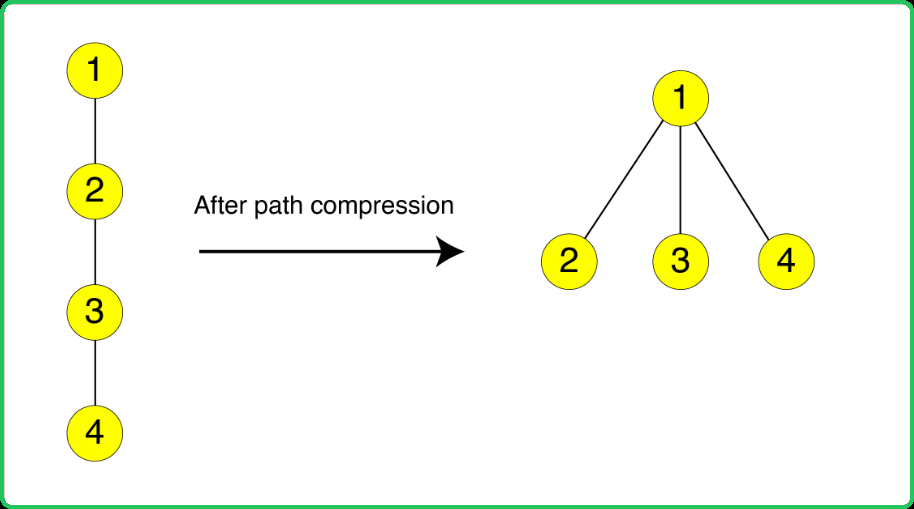
How the Time Complexity reduces? Before path compression, finding the ultimate parent for node 4 involves traversing back to node 1, which is the height of size logN. After path compression, the ultimate parent is accessed in a single step, reducing traversal and thus the time complexity.
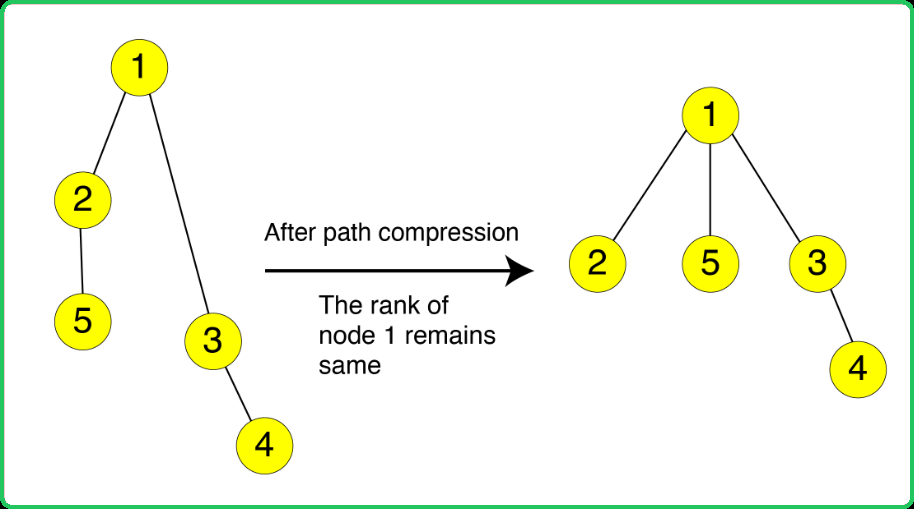
Note: We cannot change the ranks while applying path compression.
Overall, findPar() method helps to reduce the time complexity of the union by the rank method as it can find the ultimate parent within constant time. The algorithm for compressing a path is discussed below.
Algorithm:
The process of path compression can be done using the backtracking method.- Base Case: If the node and its parent are the same, return the node.
- Call the findPar() function for a node until it hits the base case. While backtracking, update the parent of the current node with the returned value.
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139
#include <bits/stdc++.h>
using namespace std;
class DisjointSet {
private:
// To store the rank of each node
vector<int> rank;
/* To store the size of components
that each node belongs to */
vector<int> size;
// To store the ultimate parent of each node
vector<int> parent;
public:
// Constructor
DisjointSet(int n) {
// Resize the arrays
rank.resize(n + 1, 0);
parent.resize(n + 1);
size.resize(n+1, 1);
// Initialise each node with its own value
for (int i = 0; i <= n; i++) {
parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
int findUPar(int node) {
// Base case
if (node == parent[node])
return node;
// Backtracking step for path compression
return parent[node] = findUPar(parent[node]);
}
/* Function to detemine if two nodes
are in the same component or not */
bool find(int u, int v) {
// Return true if both have same ultimate parent
return (findUPar(u) == findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
void unionByRank(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (rank[ulp_u] < rank[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
// Update the parent
parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the rank
rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on ranks */
void unionBySize(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (size[ulp_u] < size[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
// Update the size
size[ulp_v] += size[ulp_u];
}
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the size
size[ulp_u] += size[ulp_v];
}
}
};
int main() {
// Disjoint Data structure
DisjointSet ds(7);
ds.unionByRank(1, 2); // Adding edge between 1 and 2
ds.unionByRank(2, 3); // Adding edge between 2 and 3
ds.unionByRank(4, 5); // Adding edge between 4 and 5
ds.unionByRank(6, 7); // Adding edge between 6 and 7
ds.unionByRank(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
cout << "They belong to the same components.\n";
else
cout << "They do not belong to the same components.\n";
ds.unionByRank(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
cout << "They belong to the same components.\n";
else
cout << "They do not belong to the same components.\n";
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class DisjointSet {
// To store the rank of each node
private int[] rank;
/* To store the size of components
that each node belongs to */
private int[] size;
// To store the ultimate parent of each node
private int[] parent;
// Constructor
public DisjointSet(int n) {
// Resize the arrays
rank = new int[n + 1];
parent = new int[n + 1];
size = new int[n + 1];
Arrays.fill(size, 1);
// Initialise each node with its own value
for (int i = 0; i <= n; i++) {
parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
public int findUPar(int node) {
// Base case
if (node == parent[node])
return node;
// Backtracking step for path compression
return parent[node] = findUPar(parent[node]);
}
/* Function to determine if two nodes
are in the same component or not */
public boolean find(int u, int v) {
// Return true if both have same ultimate parent
return (findUPar(u) == findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
public void unionByRank(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (rank[ulp_u] < rank[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
} else if (rank[ulp_v] < rank[ulp_u]) {
// Update the parent
parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the rank
rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on sizes */
public void unionBySize(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (size[ulp_u] < size[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
// Update the size
size[ulp_v] += size[ulp_u];
} else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the size
size[ulp_u] += size[ulp_v];
}
}
}
public class Main {
public static void main(String[] args) {
// Disjoint Data structure
DisjointSet ds = new DisjointSet(7);
ds.unionByRank(1, 2); // Adding edge between 1 and 2
ds.unionByRank(2, 3); // Adding edge between 2 and 3
ds.unionByRank(4, 5); // Adding edge between 4 and 5
ds.unionByRank(6, 7); // Adding edge between 6 and 7
ds.unionByRank(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
System.out.println("They belong to the same components.");
else
System.out.println("They do not belong to the same components.");
ds.unionByRank(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
System.out.println("They belong to the same components.");
else
System.out.println("They do not belong to the same components.");
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
class DisjointSet:
# Constructor
def __init__(self, n):
# Resize the arrays
self.rank = [0] * (n + 1)
self.parent = [i for i in range(n + 1)]
self.size = [1] * (n + 1)
# Helper function to find ultimate
# parent along with path compression
def findUPar(self, node):
# Base case
if node == self.parent[node]:
return node
# Backtracking step for path compression
self.parent[node] = self.findUPar(self.parent[node])
return self.parent[node]
# Function to determine if two nodes
# are in the same component or not
def find(self, u, v):
# Return true if both have same ultimate parent
return self.findUPar(u) == self.findUPar(v)
# Function to perform union of
# two nodes based on ranks
def unionByRank(self, u, v):
# Get the ultimate parents of both nodes
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
# Return if nodes already belong to the same component
if ulp_u == ulp_v:
return
# Otherwise, join the node to the other
# node having higher ranks among the two
if self.rank[ulp_u] < self.rank[ulp_v]:
# Update the parent
self.parent[ulp_u] = ulp_v
elif self.rank[ulp_v] < self.rank[ulp_u]:
# Update the parent
self.parent[ulp_v] = ulp_u
else:
# Update the parent
self.parent[ulp_v] = ulp_u
# Update the rank
self.rank[ulp_u] += 1
# Function to perform union of
# two nodes based on sizes
def unionBySize(self, u, v):
# Get the ultimate parents of both nodes
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
# Return if nodes already belong to the same component
if ulp_u == ulp_v:
return
# Otherwise, join the node belonging to the smaller
# component to the node belonging to bigger component
if self.size[ulp_u] < self.size[ulp_v]:
# Update the parent
self.parent[ulp_u] = ulp_v
# Update the size
self.size[ulp_v] += self.size[ulp_u]
else:
# Update the parent
self.parent[ulp_v] = ulp_u
# Update the size
self.size[ulp_u] += self.size[ulp_v]
if __name__ == "__main__":
# Disjoint Data structure
ds = DisjointSet(7)
ds.unionByRank(1, 2) # Adding edge between 1 and 2
ds.unionByRank(2, 3) # Adding edge between 2 and 3
ds.unionByRank(4, 5) # Adding edge between 4 and 5
ds.unionByRank(6, 7) # Adding edge between 6 and 7
ds.unionByRank(5, 6) # Adding edge between 5 and 6
# Checking if node 3 and node 7
# are in the same component
if ds.find(3, 7):
print("They belong to the same components.")
else:
print("They do not belong to the same components.")
ds.unionByRank(3, 7) # Adding edge between 3 and 7
# Checking again if node 3 and node 7
# are in the same component
if ds.find(3, 7):
print("They belong to the same components.")
else:
print("They do not belong to the same components.")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116
class DisjointSet {
// Constructor
constructor(n) {
// Resize the arrays
this.rank = new Array(n + 1).fill(0);
this.parent = new Array(n + 1);
this.size = new Array(n + 1).fill(1);
// Initialise each node with its own value
for (let i = 0; i <= n; i++) {
this.parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
findUPar(node) {
// Base case
if (node === this.parent[node])
return node;
// Backtracking step for path compression
this.parent[node] = this.findUPar(this.parent[node]);
return this.parent[node];
}
/* Function to determine if two nodes
are in the same component or not */
find(u, v) {
// Return true if both have same ultimate parent
return (this.findUPar(u) === this.findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
unionByRank(u, v) {
// Get the ultimate parents of both nodes
let ulp_u = this.findUPar(u);
let ulp_v = this.findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u === ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (this.rank[ulp_u] < this.rank[ulp_v]) {
// Update the parent
this.parent[ulp_u] = ulp_v;
} else if (this.rank[ulp_v] < this.rank[ulp_u]) {
// Update the parent
this.parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
this.parent[ulp_v] = ulp_u;
// Update the rank
this.rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on sizes */
unionBySize(u, v) {
// Get the ultimate parents of both nodes
let ulp_u = this.findUPar(u);
let ulp_v = this.findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u === ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (this.size[ulp_u] < this.size[ulp_v]) {
// Update the parent
this.parent[ulp_u] = ulp_v;
// Update the size
this.size[ulp_v] += this.size[ulp_u];
} else {
// Update the parent
this.parent[ulp_v] = ulp_u;
// Update the size
this.size[ulp_u] += this.size[ulp_v];
}
}
}
const main = () => {
// Disjoint Data structure
const ds = new DisjointSet(7);
ds.unionByRank(1, 2); // Adding edge between 1 and 2
ds.unionByRank(2, 3); // Adding edge between 2 and 3
ds.unionByRank(4, 5); // Adding edge between 4 and 5
ds.unionByRank(6, 7); // Adding edge between 6 and 7
ds.unionByRank(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
console.log("They belong to the same components.");
else
console.log("They do not belong to the same components.");
ds.unionByRank(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
console.log("They belong to the same components.");
else
console.log("They do not belong to the same components.");
};
main();
Complexity Analysis:
Time Complexity: O(1)
The actual time complexity of UnionByRank() and findPar() methods is O(4α), which is very small and close to 1. This 4α term has a long mathematical derivation not required for an interview.
Space Complexity: O(2N) (where N is the number of nodes)
The Disjoint Set Data structure uses a parent and a rank array each of size N.
Introduction:
The Disjoint Set data structure is a crucial topic in the graph series. To understand its necessity, consider the following problem:
Problem Statement:
Given two components of an undirected graph, determine if node 1 and node 5 belong to the same component.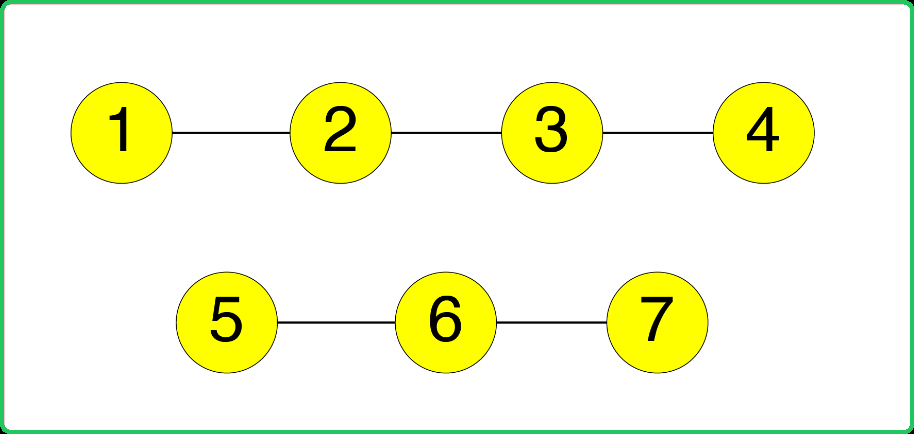
Approach:
To solve this problem, Depth-First Search (DFS) or Breadth-First Search (BFS) traversal techniques can be employed. By traversing the graph components, it is evident that node 1 and node 5 are in different components. This brute force approach has a time complexity of O(N+E) where N is the number of nodes and E is the number of edges. However, using a Disjoint Set data structure, this problem can be solved in constant time.The Disjoint Set data structure is particularly useful for dynamic graphs.
Dynamic Graph:
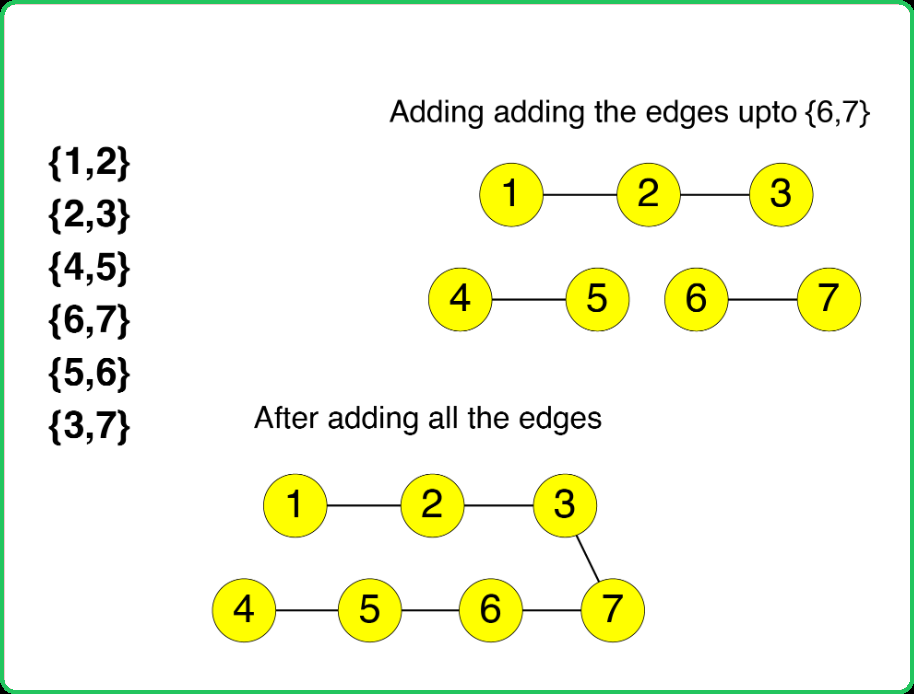
A dynamic graph refers to a graph that continuously changes its configuration.For example, consider the edge information for a graph as:
{{1,2},{2,3},{4,5},{6,7},{5,6},{3,7}} Adding edges one by one changes the structure of the graph at each step. After adding the first four edges, nodes 4 and 1 belong to different components. After adding all six edges, nodes 4 and 1 belong to the same component.
Now, to answer any query that requires checking whether two nodes belong to the same component in the graph, if the traversal techniques are used, then it will be extremely time consuming as the graph is changing every time. Here, Disjoint Set plays a crucial role. Disjoint Set can quickly determine if two arbitrary nodes u and v are in the same component at any step.
Functionalities of Disjoint Set Data Structure:
The Disjoint Set data structure provides two primary functionalities:
- Finding the parent(ultimate parent) of a particular node.
- Union operation (which adds an edge between two nodes):
- Union by Rank
- Union by Size
Implementation:
To implement Union by Size, two arrays of size N (number of nodes) are needed:
- Size array: Storing the size of each node, i.e., the size of the component starting from that node.
- Parent array: Storing the ultimate parents of each node.
Algorithm:
-
Initial Configuration:
- Size array: Initialized with all values as 1.
- Parent array: Initialized with the value of nodes, i.e., parent[i] = i.
-
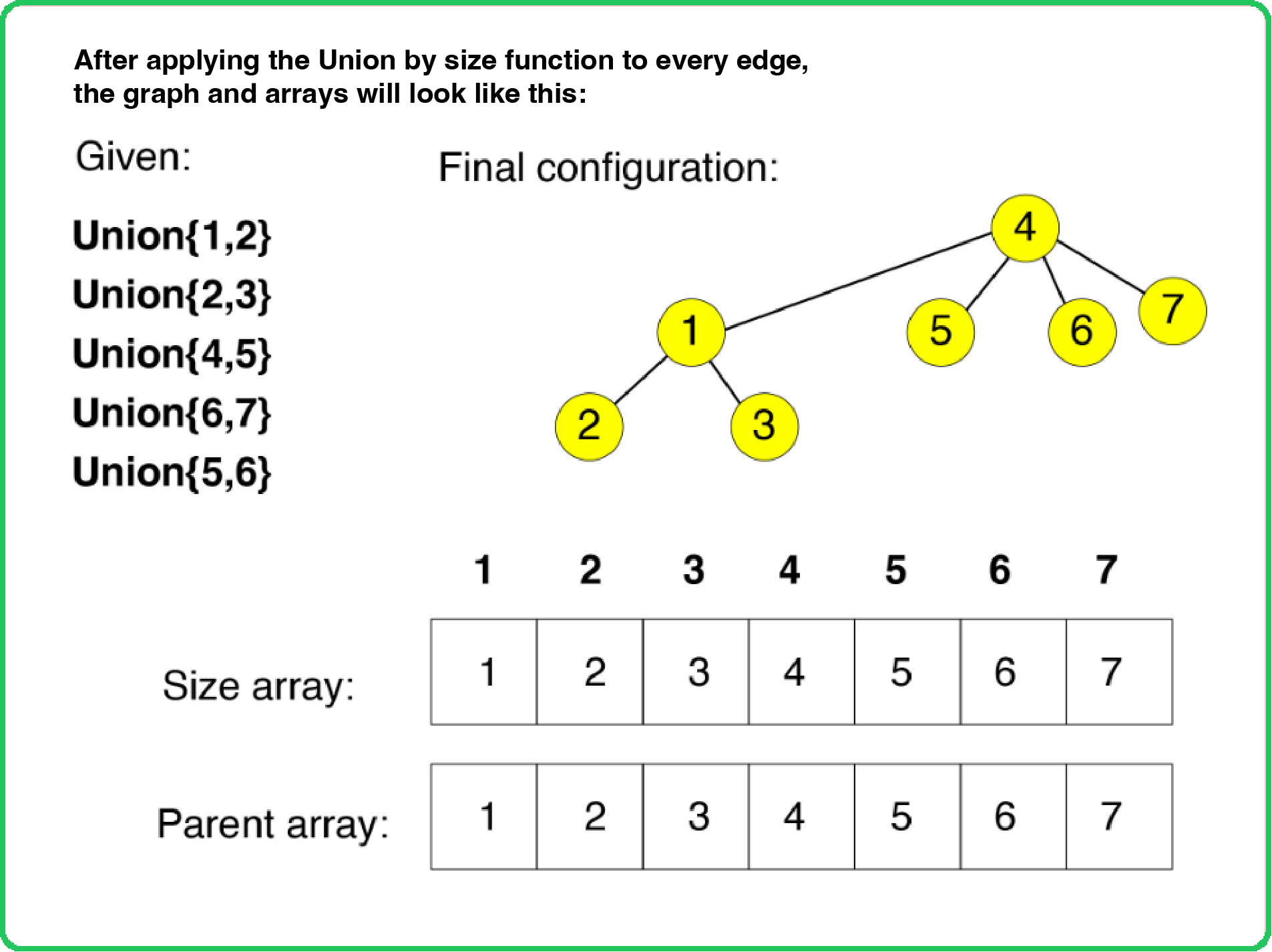
Union Function Steps:
- The Union function requires two nodes (let's say u and v) as arguments. Find the ultimate parent of u and v using the a helper findPar() function. Let pu and pv be the ultimate parents of u and v respectively.
- Determine the size of pu and pv.
- Connect the ultimate parent with a smaller size to the other ultimate parent with a larger size. If the sizes are equal, connect any parent to the other parent. While connecting in both cases, the size of the parent node (to whom the node was connected) will be increased by the size of the other parent node which is actually connected.
Example:
Given the edges of a graph as {{1,2}, {2,3}, {4,5}, {6,7}, {5,6}, {3,7}}: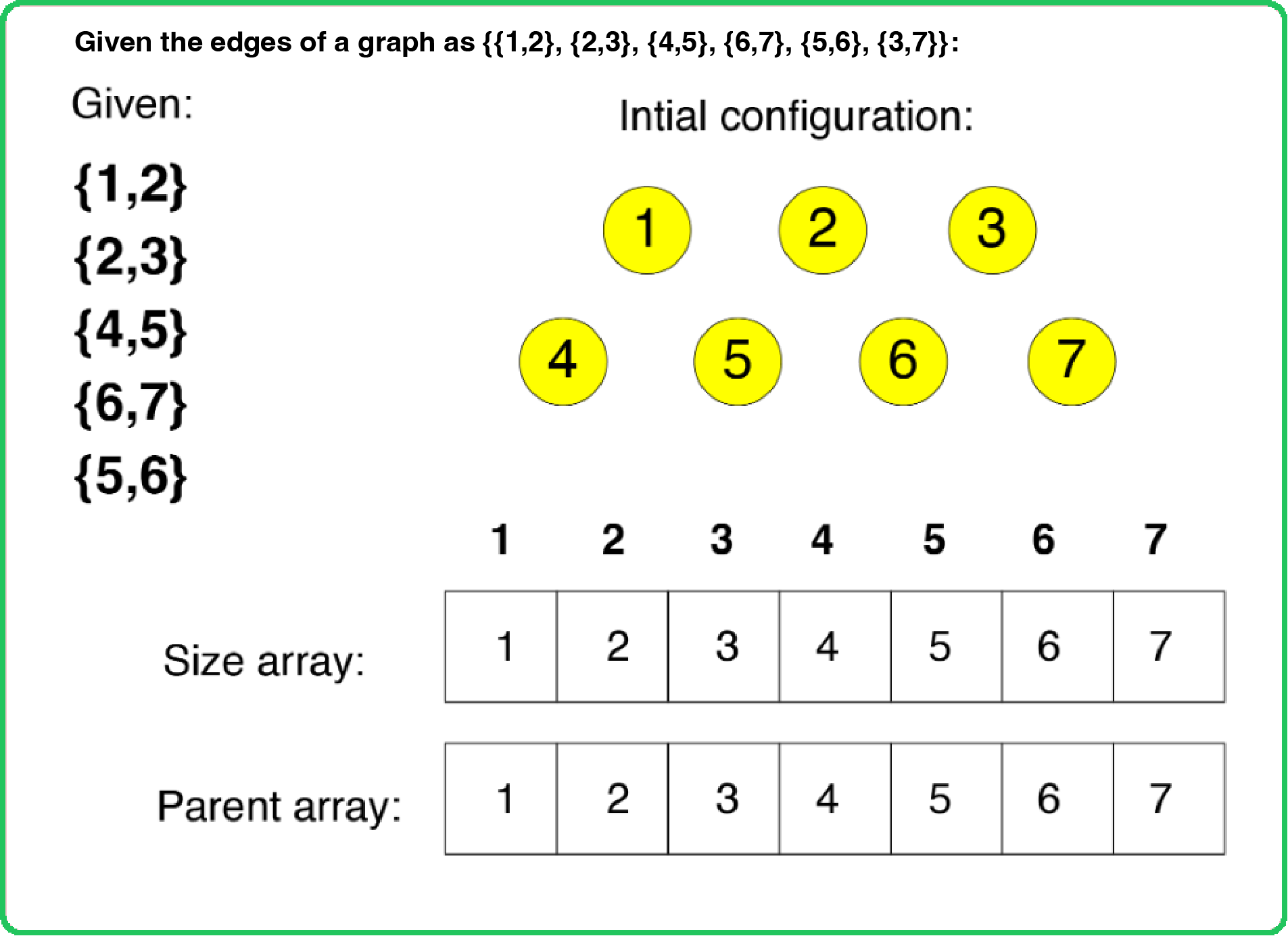
Observations:
In the Union by Rank function, the actual ranks were getting distored during the process of path compression. However, for the case of Union by Size function, there is no distortion of sizes during the process of path compression.
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141
#include <bits/stdc++.h>
using namespace std;
class DisjointSet {
private:
// To store the rank of each node
vector<int> rank;
/* To store the size of components
that each node belongs to */
vector<int> size;
// To store the ultimate parent of each node
vector<int> parent;
public:
// Constructor
DisjointSet(int n) {
// Resize the arrays
rank.resize(n + 1, 0);
parent.resize(n + 1);
size.resize(n + 1, 1);
// Initialise each node with its own value
for (int i = 0; i <= n; i++) {
parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
int findUPar(int node) {
// Base case
if (node == parent[node])
return node;
// Backtracking step for path compression
return parent[node] = findUPar(parent[node]);
}
/* Function to detemine if two nodes
are in the same component or not */
bool find(int u, int v) {
// Return true if both have same ultimate parent
return (findUPar(u) == findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
void unionByRank(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (rank[ulp_u] < rank[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
// Update the parent
parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the rank
rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on ranks */
void unionBySize(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (size[ulp_u] < size[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
// Update the size
size[ulp_v] += size[ulp_u];
}
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the size
size[ulp_u] += size[ulp_v];
}
}
};
int main() {
// Disjoint Data structure
DisjointSet ds(7);
ds.unionBySize(1, 2); // Adding edge between 1 and 2
ds.unionBySize(2, 3); // Adding edge between 2 and 3
ds.unionBySize(4, 5); // Adding edge between 4 and 5
ds.unionBySize(6, 7); // Adding edge between 6 and 7
ds.unionBySize(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
cout << "They belong to the same components.\n";
else
cout << "They do not belong to the same components.\n";
ds.unionBySize(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
cout << "They belong to the same components.\n";
else
cout << "They do not belong to the same components.\n";
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class DisjointSet {
// To store the rank of each node
private int[] rank;
/* To store the size of components
that each node belongs to */
private int[] size;
// To store the ultimate parent of each node
private int[] parent;
// Constructor
public DisjointSet(int n) {
// Resize the arrays
rank = new int[n + 1];
parent = new int[n + 1];
size = new int[n + 1];
Arrays.fill(size, 1);
// Initialise each node with its own value
for (int i = 0; i <= n; i++) {
parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
public int findUPar(int node) {
// Base case
if (node == parent[node])
return node;
// Backtracking step for path compression
return parent[node] = findUPar(parent[node]);
}
/* Function to determine if two nodes
are in the same component or not */
public boolean find(int u, int v) {
// Return true if both have same ultimate parent
return (findUPar(u) == findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
public void unionByRank(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (rank[ulp_u] < rank[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
} else if (rank[ulp_v] < rank[ulp_u]) {
// Update the parent
parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the rank
rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on sizes */
public void unionBySize(int u, int v) {
// Get the ultimate parents of both nodes
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u == ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (size[ulp_u] < size[ulp_v]) {
// Update the parent
parent[ulp_u] = ulp_v;
// Update the size
size[ulp_v] += size[ulp_u];
} else {
// Update the parent
parent[ulp_v] = ulp_u;
// Update the size
size[ulp_u] += size[ulp_v];
}
}
}
public class Main {
public static void main(String[] args) {
// Disjoint Data structure
DisjointSet ds = new DisjointSet(7);
ds.unionBySize(1, 2); // Adding edge between 1 and 2
ds.unionBySize(2, 3); // Adding edge between 2 and 3
ds.unionBySize(4, 5); // Adding edge between 4 and 5
ds.unionBySize(6, 7); // Adding edge between 6 and 7
ds.unionBySize(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
System.out.println("They belong to the same components.");
else
System.out.println("They do not belong to the same components.");
ds.unionBySize(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
System.out.println("They belong to the same components.");
else
System.out.println("They do not belong to the same components.");
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
class DisjointSet:
# Constructor
def __init__(self, n):
# Resize the arrays
self.rank = [0] * (n + 1)
self.parent = [i for i in range(n + 1)]
self.size = [1] * (n + 1)
# Helper function to find ultimate
# parent along with path compression
def findUPar(self, node):
# Base case
if node == self.parent[node]:
return node
# Backtracking step for path compression
self.parent[node] = self.findUPar(self.parent[node])
return self.parent[node]
# Function to determine if two nodes
# are in the same component or not
def find(self, u, v):
# Return true if both have same ultimate parent
return self.findUPar(u) == self.findUPar(v)
# Function to perform union of
# two nodes based on ranks
def unionByRank(self, u, v):
# Get the ultimate parents of both nodes
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
# Return if nodes already belong to the same component
if ulp_u == ulp_v:
return
# Otherwise, join the node to the other
# node having higher ranks among the two
if self.rank[ulp_u] < self.rank[ulp_v]:
# Update the parent
self.parent[ulp_u] = ulp_v
elif self.rank[ulp_v] < self.rank[ulp_u]:
# Update the parent
self.parent[ulp_v] = ulp_u
else:
# Update the parent
self.parent[ulp_v] = ulp_u
# Update the rank
self.rank[ulp_u] += 1
# Function to perform union of
# two nodes based on sizes
def unionBySize(self, u, v):
# Get the ultimate parents of both nodes
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
# Return if nodes already belong to the same component
if ulp_u == ulp_v:
return
# Otherwise, join the node belonging to the smaller
# component to the node belonging to bigger component
if self.size[ulp_u] < self.size[ulp_v]:
# Update the parent
self.parent[ulp_u] = ulp_v
# Update the size
self.size[ulp_v] += self.size[ulp_u]
else:
# Update the parent
self.parent[ulp_v] = ulp_u
# Update the size
self.size[ulp_u] += self.size[ulp_v]
if __name__ == "__main__":
# Disjoint Data structure
ds = DisjointSet(7)
ds.unionBySize(1, 2) # Adding edge between 1 and 2
ds.unionBySize(2, 3) # Adding edge between 2 and 3
ds.unionBySize(4, 5) # Adding edge between 4 and 5
ds.unionBySize(6, 7) # Adding edge between 6 and 7
ds.unionBySize(5, 6) # Adding edge between 5 and 6
# Checking if node 3 and node 7
# are in the same component
if ds.find(3, 7):
print("They belong to the same components.")
else:
print("They do not belong to the same components.")
ds.unionBySize(3, 7) # Adding edge between 3 and 7
# Checking again if node 3 and node 7
# are in the same component
if ds.find(3, 7):
print("They belong to the same components.")
else:
print("They do not belong to the same components.")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116
class DisjointSet {
// Constructor
constructor(n) {
// Resize the arrays
this.rank = new Array(n + 1).fill(0);
this.parent = new Array(n + 1);
this.size = new Array(n + 1).fill(1);
// Initialise each node with its own value
for (let i = 0; i <= n; i++) {
this.parent[i] = i;
}
}
/* Helper function to find ultimate
parent along with path compression */
findUPar(node) {
// Base case
if (node === this.parent[node])
return node;
// Backtracking step for path compression
this.parent[node] = this.findUPar(this.parent[node]);
return this.parent[node];
}
/* Function to determine if two nodes
are in the same component or not */
find(u, v) {
// Return true if both have same ultimate parent
return (this.findUPar(u) === this.findUPar(v));
}
/* Function to perform union of
two nodes based on ranks */
unionByRank(u, v) {
// Get the ultimate parents of both nodes
let ulp_u = this.findUPar(u);
let ulp_v = this.findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u === ulp_v) return;
/* Otherwise, join the node to the other
node having higher ranks among the two */
if (this.rank[ulp_u] < this.rank[ulp_v]) {
// Update the parent
this.parent[ulp_u] = ulp_v;
} else if (this.rank[ulp_v] < this.rank[ulp_u]) {
// Update the parent
this.parent[ulp_v] = ulp_u;
}
/* If both have same rank, join any node to the
other and increment the rank of the parent node */
else {
// Update the parent
this.parent[ulp_v] = ulp_u;
// Update the rank
this.rank[ulp_u]++;
}
}
/* Function to perform union of
two nodes based on sizes */
unionBySize(u, v) {
// Get the ultimate parents of both nodes
let ulp_u = this.findUPar(u);
let ulp_v = this.findUPar(v);
// Return if nodes already belong to the same component
if (ulp_u === ulp_v) return;
/* Otherwise, join the node belonging to the smaller
component to the node belonging to bigger component */
if (this.size[ulp_u] < this.size[ulp_v]) {
// Update the parent
this.parent[ulp_u] = ulp_v;
// Update the size
this.size[ulp_v] += this.size[ulp_u];
} else {
// Update the parent
this.parent[ulp_v] = ulp_u;
// Update the size
this.size[ulp_u] += this.size[ulp_v];
}
}
}
const main = () => {
// Disjoint Data structure
const ds = new DisjointSet(7);
ds.unionBySize(1, 2); // Adding edge between 1 and 2
ds.unionBySize(2, 3); // Adding edge between 2 and 3
ds.unionBySize(4, 5); // Adding edge between 4 and 5
ds.unionBySize(6, 7); // Adding edge between 6 and 7
ds.unionBySize(5, 6); // Adding edge between 5 and 6
/* Checking if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
console.log("They belong to the same components.");
else
console.log("They do not belong to the same components.");
ds.unionBySize(3, 7); // Adding edge between 3 and 7
/* Checking again if node 3 and node 7
are in the same component */
if (ds.find(3, 7))
console.log("They belong to the same components.");
else
console.log("They do not belong to the same components.");
};
main();
Complexity Analysis:
Time Complexity: O(1)
The actual time complexity of UnionBySize() and findPar() methods is O(4α), which is very small and close to 1. This 4α term has a long mathematical derivation not required for an interview.
Space Complexity: O(2N) (where N is the number of nodes)
The Disjoint Set Data structure uses a parent and a size array each of size N.
Frequently Occurring Doubts
Q: Why does Union-Find need Path Compression?
A: Without it, finding the root takes O(n) in the worst case. Path compression flattens the structure, making future lookups nearly O(1).
Q: Can we use Union by Rank and Union by Size together?
A: No, we should only use one heuristic at a time. Using both would reduce effectiveness because size-based merging does not directly track tree height.
Interview Followup Questions
Q: How would this change if nodes were added dynamically?
A: Extend parent[] and rank[]/size[] dynamically using a hash map instead of fixed arrays.
Q: What if we wanted to track the actual connected components?
A: Maintain a list of elements in each component and update it during union().
Notes
Code
✅ Testcase
Input: {'n': '5', 'nums': '[[1, 0, 1], [2, 2, 3], [3, 0, 1], [3,0, 3]]'}
Expected:
true false
true false
Actual: -
Time: -
sec
Status: Waiting
Input: {'n': '3', 'nums': '[[2, 0, 1], [2,1, 2], [3,0, 2], [3,0, 1]]'}
Expected:
true true
true true
Actual: -
Time: -
sec
Status: Waiting
Input: {'n': '5', 'nums': '[[1,0, 1], [2,3, 4], [1,1, 2], [3,0, 2], [3,1, 3]]'}
Expected:
true false
true false
Actual: -
Time: -
sec
Status: Waiting