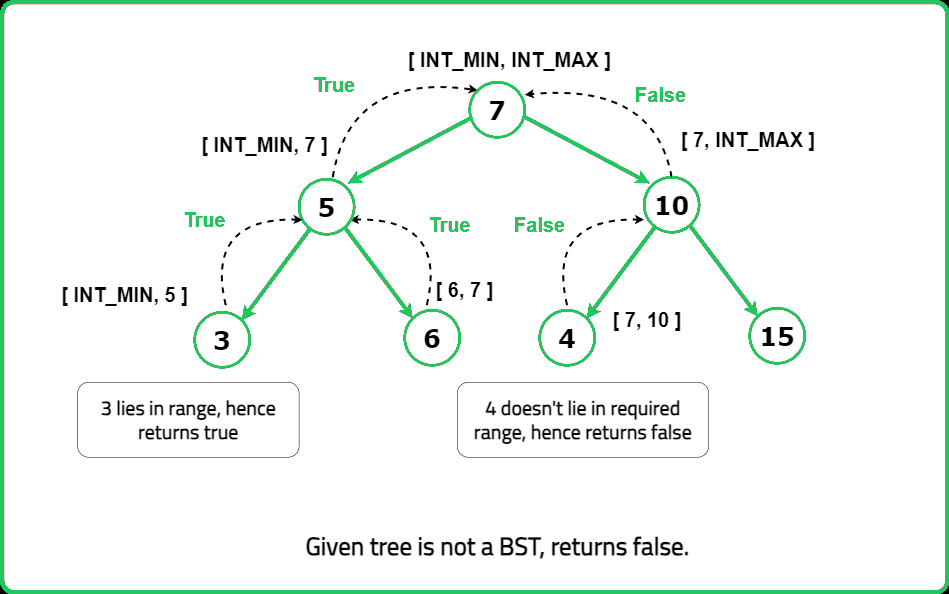
Check if a tree is a BST or not
Binary Search Trees
Medium
Medium
- Fun Fact: Checking if a binary tree is a binary search tree (BST) is not just a theoretical problem, but has practical applications in various software technologies
- Databases can utilize BSTs for indexing purposes, allowing them to perform search, insert, delete operations efficiently
- Therefore, understanding and validating BSTs are critical processes in ensuring integrity and performance in database systems
- Likewise, in languages like C++ and Java, BSTs underlie certain container types (eg
- TreeMap, TreeSet in Java, and set, multiset, map, multimap in C++) offering fast lookup, addition and removal of items
- This problem's solution can contribute to performance optimization of these containers
Given the root node of a binary tree. Return true if the given binary tree is a binary search tree(BST) else false.
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with key strictly less than the node's key.
- The right subtree of a node contains only nodes with key strictly greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Examples:
Input : root = [5, 3, 6, 2, 4, null, 7]
Output : true
Explanation : Below is image of the given tree.
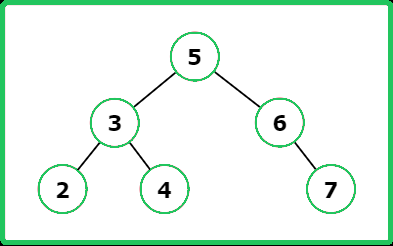
Input : root = [5, 3, 6, 4, 2, null, 7]
Output : false
Explanation : Below is image of the given tree.
The node 4 and node 2 violates the BST rule of smaller to left and larger to right.
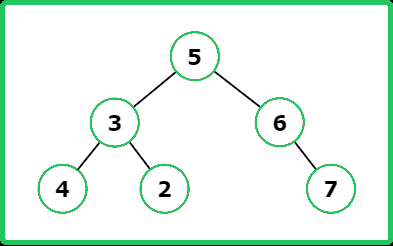
Input : root = [2, 1, 3]
Constraints
- 1 <= Number of Nodes <= 104
- -231 <= Node.val <= 231 - 1
Hints
- Recursively check. The left subtree must be within (min_val, root.val). The right subtree must be within (root.val, max_val). If a node violates the constraint, return False.
- "Perform inorder traversal (Left → Root → Right). Store previous node value while traversing. If current node value ≤ previous node value, return False."
Company Tags
Snowflake
Medtronic
HCL Technologies
Ubisoft
PwC
Red Hat
Uber
Visa
Shopify
Qualcomm
American Express
Pinterest
Ernst & Young
Intel
Roche
Reddit
Goldman Sachs
OYO Rooms
eBay
Morgan Stanley
Robinhood
Johnson & Johnson
PayPal
Bungie
Nutanix
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe