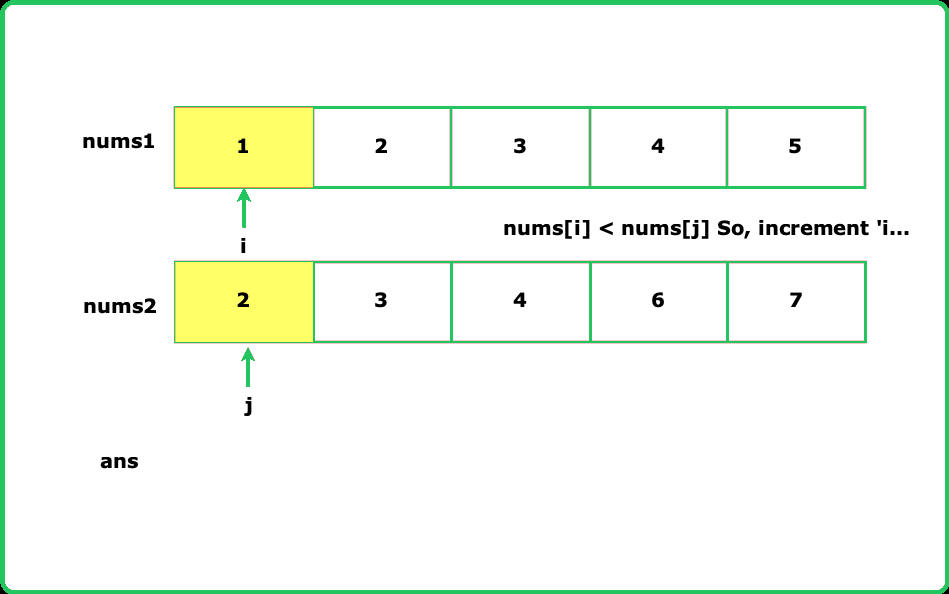
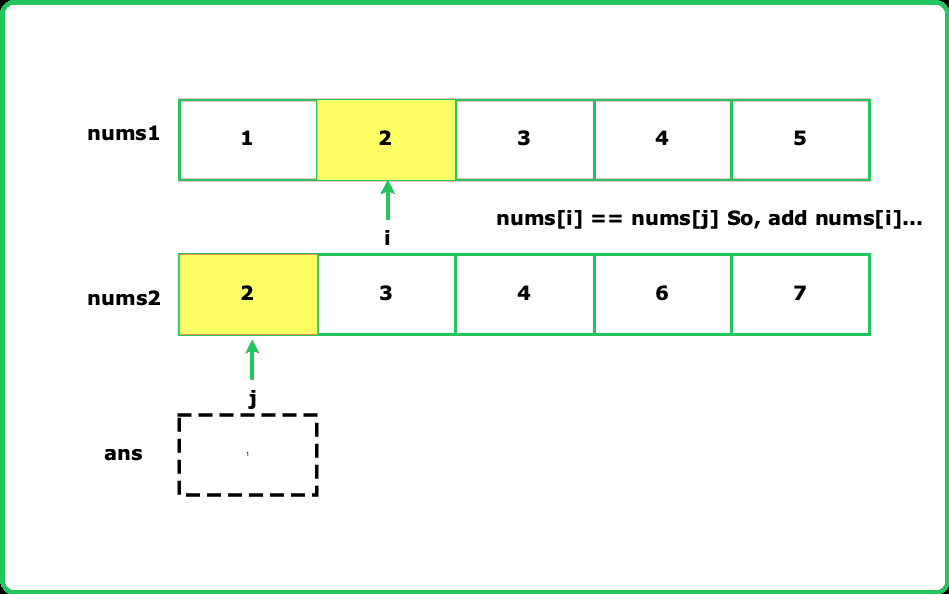
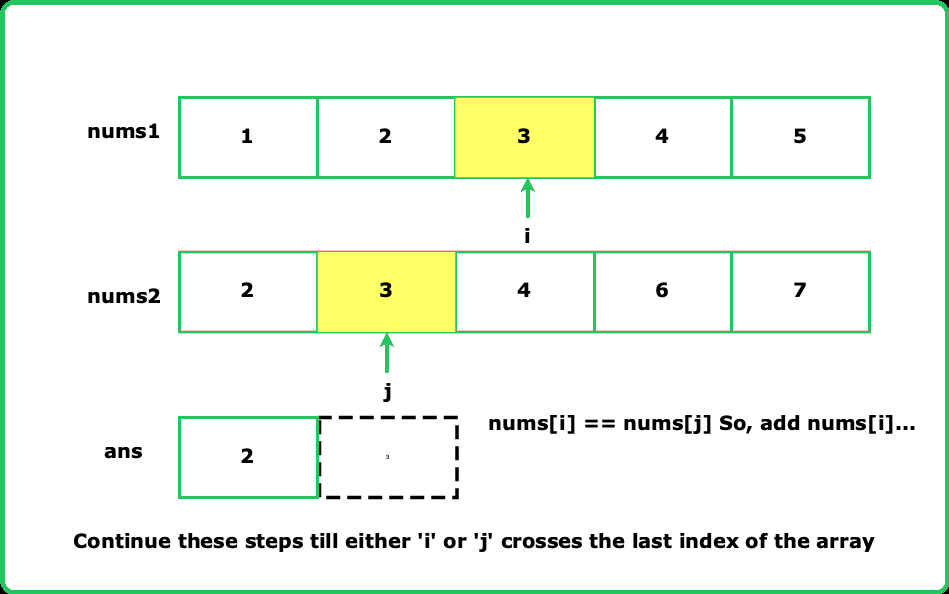
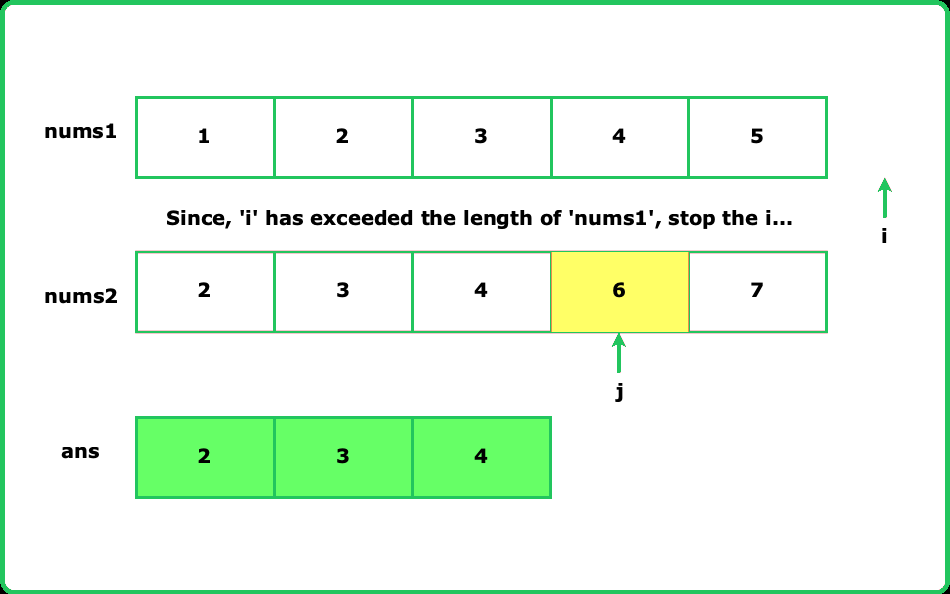
Intersection of two sorted arrays
Arrays
Logic Building
Easy
- The concept behind this problem is extremely important in database operations, specifically in the SQL operations like JOINs
- For example, an 'inner join' in SQL is essentially finding the intersection of two tables based on some common column
- This operation is used extensively in software development where handling of databases is involved
- This could include anything, from apps that need to pull up personalized user data, to large-scale data analysis and processing frameworks
Given two sorted arrays nums1 and nums2, return an array containing the intersection of these two arrays.
The intersection of two arrays is an array where all values are present in both arrays.
Examples:
Input: nums1 = [1, 2, 2, 3, 5], nums2 = [1, 2, 7]
Output: [1, 2]
Explanation: The elements 1, 2 are the only elements present in both nums1 and nums2
Input: nums1 = [1, 2, 2, 3], nums2 = [4, 5, 7]
Output: []
Explanation: No elements appear in both nums1 and nums2
Input: nums1 = [-45, -45, 0, 0, 2], nums2 = [-50, -45, 0, 0, 5, 7]
Constraints
- 1 <= nums1.length, nums2.length <= 1000
- -104 <= nums1[i], nums2[i] <= 104
- Both nums1 and nums2 are sorted in non-decreasing order.
Hints
- Use two pointers to traverse both arrays simultaneously. This helps efficiently find common elements since both arrays are sorted.Add an element to the intersection only if it is present in both arrays at the same index of the pointers.
- If duplicates are not allowed in the result, skip consecutive duplicate elements in either array during traversal.
Company Tags
Zoho
Ernst & Young
Stripe
Dropbox
Johnson & Johnson
Bungie
Walmart
Siemens Healthineers
Goldman Sachs
Byju's
Morgan Stanley
Zynga
Bloomberg
GE Healthcare
Reddit
Cloudflare
AMD
Airbnb
Swiggy
Deloitte
Seagate Technology
Cerner
Texas Instruments
Snowflake
Boston Consulting Group
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro