Sum of Subarray Ranges
Stack / Queues
Monotonic Stack
Medium
- Fact: The concept underlying this problem is extensively used in financial and data analysis software
- In the finance industry, similar algorithms can be applied to analyze the volatility of stock prices over various sub periods
- Likewise, in data analysis platforms, they can calculate metrics such as range of values over sliding windows
- Calculating the range is a crucial part of identifying the spread of data which can provide insight into the level of variability or volatility within a dataset
Given an integer array nums, determine the range of a subarray, defined as the difference between the largest and smallest elements within the subarray. Calculate and return the sum of all subarray ranges of nums.
A subarray is defined as a contiguous, non-empty sequence of elements within the array.
Examples:
Input: nums = [1, 2, 3]
Output: 4
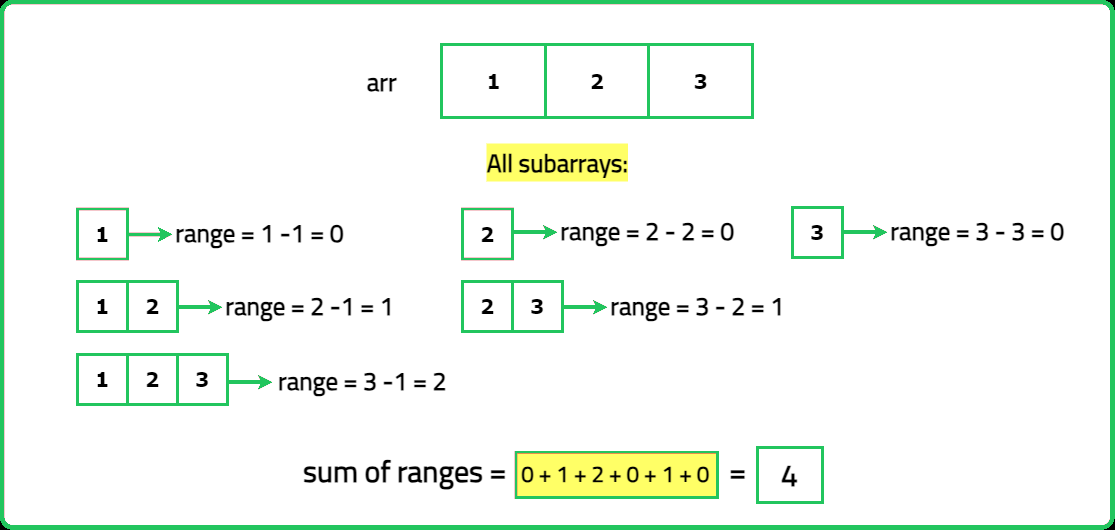
Explanation: The 6 subarrays of nums are the following:
[1], range = largest - smallest = 1 - 1 = 0
[2], range = 2 - 2 = 0
[3], range = 3 - 3 = 0
[1,2], range = 2 - 1 = 1
[2,3], range = 3 - 2 = 1
[1,2,3], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
Input: nums = [1, 3, 3]
Output: 4
Explanation: The 6 subarrays of nums are the following:
[1], range = largest - smallest = 1 - 1 = 0
[3], range = 3 - 3 = 0
[3], range = 3 - 3 = 0
[1,3], range = 3 - 1 = 2
[3,3], range = 3 - 3 = 0
[1,3,3], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
Input: nums = [4, -2, -3, 4, 1]
Constraints
· 1 <= nums.length <= 1000
· -109 <= nums[i] <= 109
Hints
- Use two monotonic stacks. One to track next greater elements (for maximum contribution). Another to track next smaller elements (for minimum contribution).
- Compute Left bound and Right Bound. The result is the difference between sum of maximum - minimum contributions.
Company Tags
Splunk
Twilio
Alibaba
Optum
Texas Instruments
NVIDIA
GE Healthcare
Freshworks
Deloitte
Johnson & Johnson
Zomato
Roche
Nutanix
JPMorgan Chase
OYO Rooms
ARM
PayPal
HashiCorp
Instacart
Airbnb
Intel
Unity Technologies
Teladoc Health
Epic Systems
Walmart
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The brute force way to solve this problem is by generating all the subarrays and finding the minimum and maximum values in all of them. The range of a subarray can be found as the difference between the maximum and minimum value which can be summed up for all the subarrays to get the result.
Approach:
- Initialize a variable to store the required sum with 0 initially.
- Traverse on the array. Initialize two variables to store the minimum and maximum elements in the subarray.
- Use a nested loop to traverse all the subarrays and find the minimum and maximum of each subarray. Update the sum for each subarray by finding the range of subarray (maximum-minimum).
- Once all the subarrays are taken into consideration, the result will be stored in the sum variable.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the sum of
subarray ranges in each subarray */
long long subArrayRanges(vector<int> &arr) {
// Size of array
int n = arr.size();
// To store the sum
long long sum = 0;
// Traverse on the array
for(int i=0; i < n; i++) {
// To store the smallest value of subarray
int smallest = arr[i];
// To store the largest value of subarray
int largest = arr[i];
/* Nested loop to get all
subarrays starting from index i */
for(int j=i; j < n; j++) {
// Update the smallest value
smallest = min(smallest, arr[j]);
// Update the largest value
largest = max(largest, arr[j]);
// Update the sum
sum += (largest - smallest);
}
}
// Return the computed sum
return sum;
}
};
int main() {
vector<int> arr = {1, 2, 3};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the sum of
subarray ranges in each subarray */
long long ans = sol.subArrayRanges(arr);
cout << "The sum of subarray ranges is: " << ans;
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
import java.util.*;
class Solution {
/* Function to find the sum of
subarray ranges in each subarray */
public long subArrayRanges(int[] arr) {
// Size of array
int n = arr.length;
// To store the sum
long sum = 0;
// Traverse on the array
for (int i = 0; i < n; i++) {
// To store the smallest value of subarray
int smallest = arr[i];
// To store the largest value of subarray
int largest = arr[i];
/* Nested loop to get all
subarrays starting from index i */
for (int j = i; j < n; j++) {
// Update the smallest value
smallest = Math.min(smallest, arr[j]);
// Update the largest value
largest = Math.max(largest, arr[j]);
// Update the sum
sum += (largest - smallest);
}
}
// Return the computed sum
return sum;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the sum of
subarray ranges in each subarray */
long ans = sol.subArrayRanges(arr);
System.out.println("The sum of subarray ranges is: " + ans);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849
class Solution:
# Function to find the sum of
# subarray ranges in each subarray
def subArrayRanges(self, arr):
# Size of array
n = len(arr)
# To store the sum
total_sum = 0
# Traverse on the array
for i in range(n):
# To store the smallest value of subarray
smallest = arr[i]
# To store the largest value of subarray
largest = arr[i]
# Nested loop to get all
# subarrays starting from index i
for j in range(i, n):
# Update the smallest value
smallest = min(smallest, arr[j])
# Update the largest value
largest = max(largest, arr[j])
# Update the sum
total_sum += (largest - smallest)
# Return the computed sum
return total_sum
# Main function to test the solution
if __name__ == "__main__":
arr = [1, 2, 3]
# Creating an instance of Solution class
sol = Solution()
# Function call to find the sum of
# subarray ranges in each subarray
ans = sol.subArrayRanges(arr)
print("The sum of subarray ranges is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
class Solution {
/* Function to find the sum of
subarray ranges in each subarray */
subArrayRanges(arr) {
// Size of array
const n = arr.length;
// To store the sum
let sum = 0;
// Traverse on the array
for (let i = 0; i < n; i++) {
// To store the smallest value of subarray
let smallest = arr[i];
// To store the largest value of subarray
let largest = arr[i];
/* Nested loop to get all
subarrays starting from index i */
for (let j = i; j < n; j++) {
// Update the smallest value
smallest = Math.min(smallest, arr[j]);
// Update the largest value
largest = Math.max(largest, arr[j]);
// Update the sum
sum += (largest - smallest);
}
}
// Return the computed sum
return sum;
}
}
// Main function to test the solution
const arr = [1, 2, 3];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to find the sum of
subarray ranges in each subarray */
const ans = sol.subArrayRanges(arr);
console.log("The sum of subarray ranges is:", ans);
Complexity Analysis:
Time Complexity: O(N2) (where N is the size of the array)
Using two nested loops.
Space Complexity: O(1)
Using only a couple of variables.
Pre Requisites: Sum of Subarray Minimums (Optimal Solution)
Intuition:
Consider the following example:
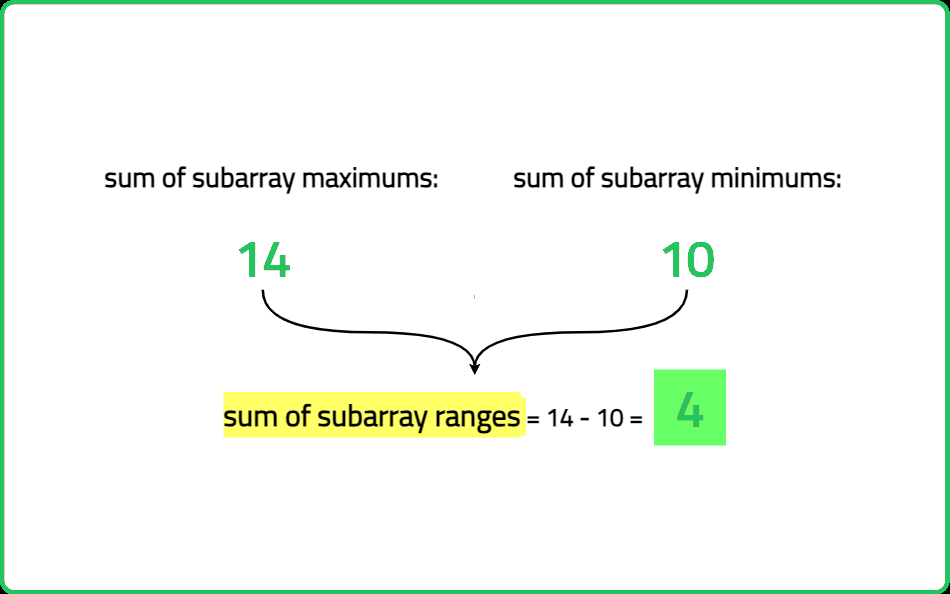
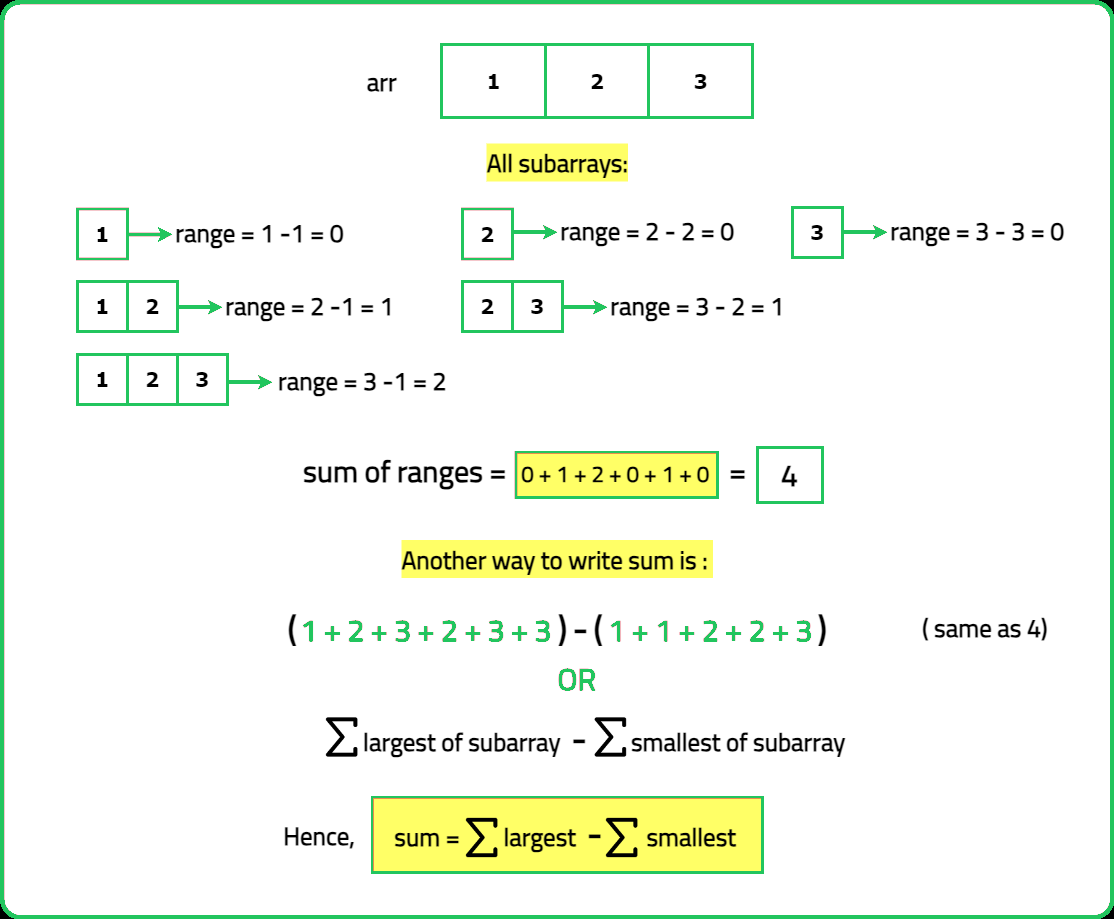Hence, instead of summing up the ranges for each subarray, the sum of largest elements in each subarray and sum of smallest elements in each subarray can be added to get the required sum of subarray ranges.
To optimally find the sum of largest and the smallest elements in the array, the concept of Next/Previous Smaller/Greater Elements come into picture as discussed in the Sum of Subarray minimums (Optimal Solution).
Approach:
- Four helper functions are used to find specific indices:
- Next Smaller Elements (NSE): For each element, find the index of the next smaller element to its right.
- Next Greater Elements (NGE): For each element, find the index of the next greater element to its right.
- Previous Smaller or Equal Elements (PSEE): For each element, find the index of the previous smaller or equal element to its left.
- Previous Greater or Equal Elements (PGEE): For each element, find the index of the previous greater or equal element to its left.
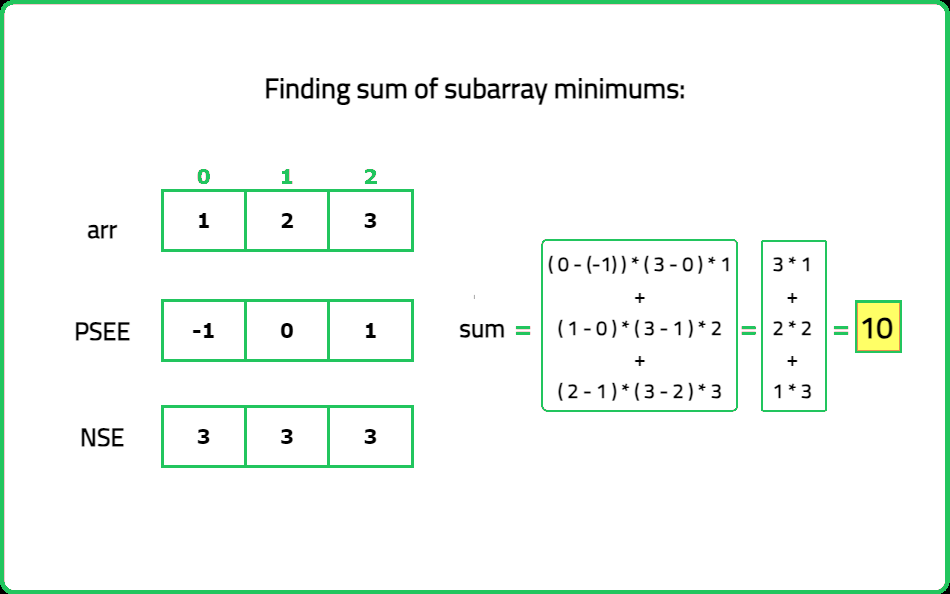
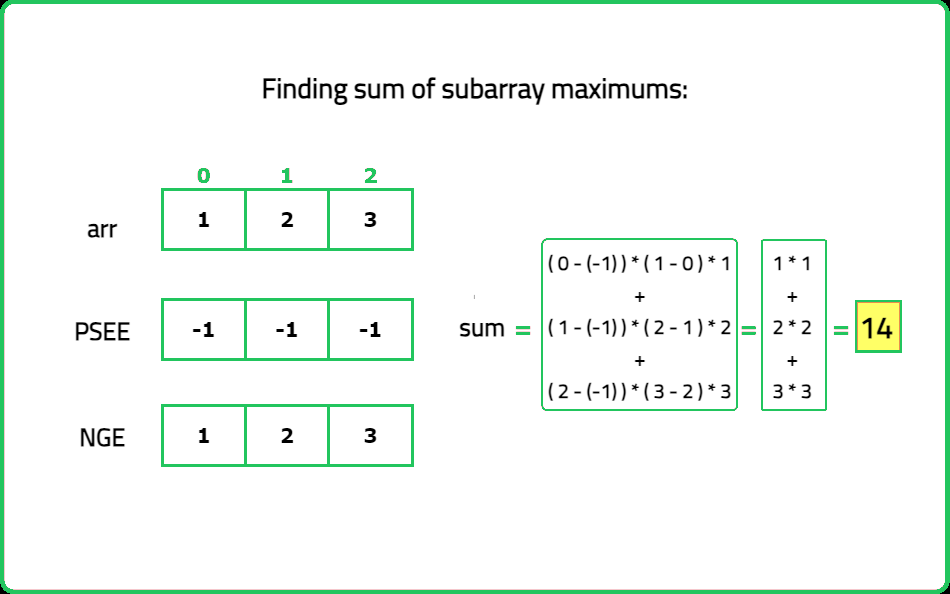
- Utilize the NSE and PSEE indices to calculate the sum of the minimum values in all subarrays. Utilize the NGE and PGEE indices to calculate the sum of the maximum values in all subarrays.
- The final result is obtained by subtracting the sum of subarray minimums from the sum of subarray maximums. This gives the sum of ranges of all subarrays.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to find the indices of
next smaller elements */
vector<int> findNSE(vector<int> &arr) {
// Size of array
int n = arr.size();
// To store the answer
vector<int> ans(n);
// Stack
stack<int> st;
// Start traversing from the back
for(int i = n - 1; i >= 0; i--) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the smaller element */
while(!st.empty() && arr[st.top()] >= arr[i]){
st.pop();
}
// Update the answer
ans[i] = !st.empty() ? st.top() : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
next greater elements */
vector<int> findNGE(vector<int> &arr) {
// Size of array
int n = arr.size();
// To store the answer
vector<int> ans(n);
// Stack
stack<int> st;
// Start traversing from the back
for(int i = n - 1; i >= 0; i--) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while(!st.empty() && arr[st.top()] <= arr[i]){
st.pop();
}
// Update the answer
ans[i] = !st.empty() ? st.top() : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous smaller or equal elements */
vector<int> findPSEE(vector<int> &arr) {
// Size of array
int n = arr.size();
// To store the answer
vector<int> ans(n);
// Stack
stack<int> st;
// Traverse on the array
for(int i=0; i < n; i++) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are greater than the current element */
while(!st.empty() && arr[st.top()] > arr[i]){
st.pop();
}
// Update the answer
ans[i] = !st.empty() ? st.top() : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous greater or equal elements */
vector<int> findPGEE(vector<int> &arr) {
// Size of array
int n = arr.size();
// To store the answer
vector<int> ans(n);
// Stack
stack<int> st;
// Traverse on the array
for(int i=0; i < n; i++) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are smaller than the current element */
while(!st.empty() && arr[st.top()] < arr[i]){
st.pop();
}
// Update the answer
ans[i] = !st.empty() ? st.top() : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the sum of the
minimum value in each subarray */
long long sumSubarrayMins(vector<int> &arr) {
vector<int> nse = findNSE(arr);
vector<int> psee = findPSEE(arr);
// Size of array
int n = arr.size();
// To store the sum
long long sum = 0;
// Traverse on the array
for(int i=0; i < n; i++) {
// Count of first type of subarrays
int left = i - psee[i];
// Count of second type of subarrays
int right = nse[i] - i;
/* Count of subarrays where
current element is minimum */
long long freq = left*right*1LL;
// Contribution due to current element
long long val = (freq*arr[i]*1LL);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
/* Function to find the sum of the
maximum value in each subarray */
long long sumSubarrayMaxs(vector<int> &arr) {
vector<int> nge = findNGE(arr);
vector<int> pgee = findPGEE(arr);
// Size of array
int n = arr.size();
// To store the sum
long long sum = 0;
// Traverse on the array
for(int i=0; i < n; i++) {
// Count of first type of subarrays
int left = i - pgee[i];
// Count of second type of subarrays
int right = nge[i] - i;
/* Count of subarrays where
current element is minimum */
long long freq = left*right*1LL;
// Contribution due to current element
long long val = (freq*arr[i]*1LL);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
public:
/* Function to find the sum of
subarray ranges in each subarray */
long long subArrayRanges(vector<int> &arr) {
// Return the result
return ( sumSubarrayMaxs(arr) -
sumSubarrayMins(arr) );
}
};
int main() {
vector<int> arr = {1, 2, 3};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the sum of
subarray ranges in each subarray */
long long ans = sol.subArrayRanges(arr);
cout << "The sum of subarray ranges is: " << ans;
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256
import java.util.*;
class Solution {
/* Function to find the indices of
next smaller elements */
private int[] findNSE(int[] arr) {
// Size of array
int n = arr.length;
// To store the answer
int[] ans = new int[n];
// Stack
Stack<Integer> st = new Stack<>();
// Start traversing from the back
for (int i = n - 1; i >= 0; i--) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the smaller element */
while (!st.isEmpty() && arr[st.peek()] >= arr[i]) {
st.pop();
}
// Update the answer
ans[i] = !st.isEmpty() ? st.peek() : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
next greater elements */
private int[] findNGE(int[] arr) {
// Size of array
int n = arr.length;
// To store the answer
int[] ans = new int[n];
// Stack
Stack<Integer> st = new Stack<>();
// Start traversing from the back
for (int i = n - 1; i >= 0; i--) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while (!st.isEmpty() && arr[st.peek()] <= arr[i]) {
st.pop();
}
// Update the answer
ans[i] = !st.isEmpty() ? st.peek() : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous smaller or equal elements */
private int[] findPSEE(int[] arr) {
// Size of array
int n = arr.length;
// To store the answer
int[] ans = new int[n];
// Stack
Stack<Integer> st = new Stack<>();
// Traverse on the array
for (int i = 0; i < n; i++) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are greater than the current element */
while (!st.isEmpty() && arr[st.peek()] > arr[i]) {
st.pop();
}
// Update the answer
ans[i] = !st.isEmpty() ? st.peek() : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous greater or equal elements */
private int[] findPGEE(int[] arr) {
// Size of array
int n = arr.length;
// To store the answer
int[] ans = new int[n];
// Stack
Stack<Integer> st = new Stack<>();
// Traverse on the array
for (int i = 0; i < n; i++) {
// Get the current element
int currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are smaller than the current element */
while (!st.isEmpty() && arr[st.peek()] < arr[i]) {
st.pop();
}
// Update the answer
ans[i] = !st.isEmpty() ? st.peek() : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the sum of the
minimum value in each subarray */
private long sumSubarrayMins(int[] arr) {
int[] nse = findNSE(arr);
int[] psee = findPSEE(arr);
// Size of array
int n = arr.length;
// To store the sum
long sum = 0;
// Traverse on the array
for (int i = 0; i < n; i++) {
// Count of first type of subarrays
int left = i - psee[i];
// Count of second type of subarrays
int right = nse[i] - i;
/* Count of subarrays where
current element is minimum */
long freq = left * right * 1L;
// Contribution due to current element
long val = (freq * arr[i] * 1L);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
/* Function to find the sum of the
maximum value in each subarray */
private long sumSubarrayMaxs(int[] arr) {
int[] nge = findNGE(arr);
int[] pgee = findPGEE(arr);
// Size of array
int n = arr.length;
// To store the sum
long sum = 0;
// Traverse on the array
for (int i = 0; i < n; i++) {
// Count of first type of subarrays
int left = i - pgee[i];
// Count of second type of subarrays
int right = nge[i] - i;
/* Count of subarrays where
current element is maximum */
long freq = left * right * 1L;
// Contribution due to current element
long val = (freq * arr[i] * 1L);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
/* Function to find the sum of
subarray ranges in each subarray */
public long subArrayRanges(int[] arr) {
// Return the result
return ( sumSubarrayMaxs(arr) -
sumSubarrayMins(arr) );
}
public static void main(String[] args) {
int[] arr = {1, 2, 3};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the sum of
subarray ranges in each subarray */
long ans = sol.subArrayRanges(arr);
System.out.println("The sum of subarray ranges is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230
class Solution:
# Function to find the indices of
# next smaller elements
def findNSE(self, arr):
# Size of array
n = len(arr)
# To store the answer
ans = [0] * n
# Stack
st = []
# Start traversing from the back
for i in range(n - 1, -1, -1):
# Get the current element
currEle = arr[i]
# Pop the elements in the stack until
# the stack is not empty and the top
# element is not the smaller element
while st and arr[st[-1]] >= arr[i]:
st.pop()
# Update the answer
ans[i] = st[-1] if st else n
# Push the index of current element in the stack
st.append(i)
# Return the answer
return ans
# Function to find the indices of
# next greater elements
def findNGE(self, arr):
# Size of array
n = len(arr)
# To store the answer
ans = [0] * n
# Stack
st = []
# Start traversing from the back
for i in range(n - 1, -1, -1):
# Get the current element
currEle = arr[i]
# Pop the elements in the stack until
# the stack is not empty and the top
# element is not the greater element
while st and arr[st[-1]] <= arr[i]:
st.pop()
# Update the answer
ans[i] = st[-1] if st else n
# Push the index of current element in the stack
st.append(i)
# Return the answer
return ans
# Function to find the indices of
# previous smaller or equal elements
def findPSEE(self, arr):
# Size of array
n = len(arr)
# To store the answer
ans = [0] * n
# Stack
st = []
# Traverse on the array
for i in range(n):
# Get the current element
currEle = arr[i]
# Pop the elements in the stack until
# the stack is not empty and the top
# elements are greater than the current element
while st and arr[st[-1]] > arr[i]:
st.pop()
# Update the answer
ans[i] = st[-1] if st else -1
# Push the index of current element in the stack
st.append(i)
# Return the answer
return ans
# Function to find the indices of
# previous greater or equal elements
def findPGEE(self, arr):
# Size of array
n = len(arr)
# To store the answer
ans = [0] * n
# Stack
st = []
# Traverse on the array
for i in range(n):
# Get the current element
currEle = arr[i]
# Pop the elements in the stack until
# the stack is not empty and the top
# elements are smaller than the current element
while st and arr[st[-1]] < arr[i]:
st.pop()
# Update the answer
ans[i] = st[-1] if st else -1
# Push the index of current element in the stack
st.append(i)
# Return the answer
return ans
# Function to find the sum of the
# minimum value in each subarray
def sumSubarrayMins(self, arr):
nse = self.findNSE(arr)
psee = self.findPSEE(arr)
# Size of array
n = len(arr)
# To store the sum
total_sum = 0
# Traverse on the array
for i in range(n):
# Count of first type of subarrays
left = i - psee[i]
# Count of second type of subarrays
right = nse[i] - i
# Count of subarrays where
# current element is minimum
freq = left * right * 1
# Contribution due to current element
val = (freq * arr[i] * 1)
# Updating the sum
total_sum += val
# Return the computed sum
return total_sum
# Function to find the sum of the
# maximum value in each subarray
def sumSubarrayMaxs(self, arr):
nge = self.findNGE(arr)
pgee = self.findPGEE(arr)
# Size of array
n = len(arr)
# To store the sum
total_sum = 0
# Traverse on the array
for i in range(n):
# Count of first type of subarrays
left = i - pgee[i]
# Count of second type of subarrays
right = nge[i] - i
# Count of subarrays where
# current element is maximum
freq = left * right * 1
# Contribution due to current element
val = (freq * arr[i] * 1)
# Updating the sum
total_sum += val
# Return the computed sum
return total_sum
# Function to find the sum of
# subarray ranges in each subarray
def subArrayRanges(self, arr):
# Return the result
return (self.sumSubarrayMaxs(arr) -
self.sumSubarrayMins(arr))
# Main function to test the solution
if __name__ == "__main__":
arr = [1, 2, 3]
# Creating an instance of Solution class
sol = Solution()
# Function call to find the sum of
# subarray ranges in each subarray
ans = sol.subArrayRanges(arr)
print("The sum of subarray ranges is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253
class Solution {
/* Function to find the indices of
next smaller elements */
findNSE(arr) {
// Size of array
const n = arr.length;
// To store the answer
const ans = new Array(n).fill(0);
// Stack
const st = [];
// Start traversing from the back
for (let i = n - 1; i >= 0; i--) {
// Get the current element
const currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the smaller element */
while (st.length > 0 && arr[st[st.length - 1]] >= arr[i]) {
st.pop();
}
// Update the answer
ans[i] = st.length > 0 ? st[st.length - 1] : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
next greater elements */
findNGE(arr) {
// Size of array
const n = arr.length;
// To store the answer
const ans = new Array(n).fill(0);
// Stack
const st = [];
// Start traversing from the back
for (let i = n - 1; i >= 0; i--) {
// Get the current element
const currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while (st.length > 0 && arr[st[st.length - 1]] <= arr[i]) {
st.pop();
}
// Update the answer
ans[i] = st.length > 0 ? st[st.length - 1] : n;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous smaller or equal elements */
findPSEE(arr) {
// Size of array
const n = arr.length;
// To store the answer
const ans = new Array(n).fill(0);
// Stack
const st = [];
// Traverse on the array
for (let i = 0; i < n; i++) {
// Get the current element
const currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are greater than the current element */
while (st.length > 0 && arr[st[st.length - 1]] > arr[i]) {
st.pop();
}
// Update the answer
ans[i] = st.length > 0 ? st[st.length - 1] : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the indices of
previous greater or equal elements */
findPGEE(arr) {
// Size of array
const n = arr.length;
// To store the answer
const ans = new Array(n).fill(0);
// Stack
const st = [];
// Traverse on the array
for (let i = 0; i < n; i++) {
// Get the current element
const currEle = arr[i];
/* Pop the elements in the stack until
the stack is not empty and the top
elements are smaller than the current element */
while (st.length > 0 && arr[st[st.length - 1]] < arr[i]) {
st.pop();
}
// Update the answer
ans[i] = st.length > 0 ? st[st.length - 1] : -1;
/* Push the index of current
element in the stack */
st.push(i);
}
// Return the answer
return ans;
}
/* Function to find the sum of the
minimum value in each subarray */
sumSubarrayMins(arr) {
const nse = this.findNSE(arr);
const psee = this.findPSEE(arr);
// Size of array
const n = arr.length;
// To store the sum
let sum = 0;
// Traverse on the array
for (let i = 0; i < n; i++) {
// Count of first type of subarrays
const left = i - psee[i];
// Count of second type of subarrays
const right = nse[i] - i;
/* Count of subarrays where
current element is minimum */
const freq = left * right * 1;
// Contribution due to current element
const val = (freq * arr[i] * 1);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
/* Function to find the sum of the
maximum value in each subarray */
sumSubarrayMaxs(arr) {
const nge = this.findNGE(arr);
const pgee = this.findPGEE(arr);
// Size of array
const n = arr.length;
// To store the sum
let sum = 0;
// Traverse on the array
for (let i = 0; i < n; i++) {
// Count of first type of subarrays
const left = i - pgee[i];
// Count of second type of subarrays
const right = nge[i] - i;
/* Count of subarrays where
current element is maximum */
const freq = left * right * 1;
// Contribution due to current element
const val = (freq * arr[i] * 1);
// Updating the sum
sum += val;
}
// Return the computed sum
return sum;
}
/* Function to find the sum of
subarray ranges in each subarray */
subArrayRanges(arr) {
// Return the result
return ( this.sumSubarrayMaxs(arr) -
this.sumSubarrayMins(arr) );
}
}
// Main function to test the solution
const arr = [1, 2, 3];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to find the sum of
subarray ranges in each subarray */
const ans = sol.subArrayRanges(arr);
console.log("The sum of subarray ranges is:", ans);
Complexity Analysis:
Time Complexity: O(N) (where N is the size of given array)
- Calculating the sum of subarray maximums takes O(N) time.
- Calculating the sum of subarray minimums takes O(N) time.
Space Complexity: O(N)
- Calculating the sum of subarray maximums requires O(N) space.
- Calculating the sum of subarray minimums requires O(N) space.
Frequently Occurring Doubts
Q: How does the stack help compute min/max contributions?
A: The stack keeps track of previously encountered elements and allows quick retrieval of how many subarrays an element influences.
Q: Why do we process both left and right boundaries?
A: To efficiently count how many subarrays include an element as the max or min.
Interview Followup Questions
Q: Can this be extended to finding the sum of absolute differences of subarrays?
A: Yes, a similar monotonic stack technique can be used to count contributions efficiently.
Q: How does this approach compare to brute-force solutions?
A: Brute force takes O(n²), while the stack-based approach reduces it to O(n).
Notes
Code
✅ Testcase
Input: {'nums': '[1, 2, 3]'}
Expected:
4
4
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[1, 3, 3]'}
Expected:
4
4
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[4, -2, -3, 4, 1]'}
Expected:
59
59
Actual: -
Time: -
sec
Status: Waiting