1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to perform DFS traversal
void dfs(int node, vector<int> adj[],
vector<int> &vis,
stack <int> &st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all the neighbors
for(auto it : adj[node]) {
// If not visited, recursively perform DFS.
if(vis[it] == 0) dfs(it, adj, vis, st);
}
/* Add the current node to stack
once all the nodes connected to it
have been processed */
st.push(node);
}
public:
/* Function to return list containing
vertices in Topological order */
vector<int> topoSort(int V, vector<int> adj[])
{
// To store the result
vector <int> ans;
/* Stack to store processed
nodes in reverse order */
stack <int> st;
// Visited array
vector<int> vis(V, 0);
// Traverse the graph
for(int i=0; i<V; i++) {
// Start DFS traversal for unvisited node
if(!vis[i]) {
dfs(i, adj, vis, st);
}
}
// Until the stack is empty
while(!st.empty()) {
// Add the top of stack to result
ans.push_back(st.top());
// Pop the top node
st.pop();
}
// Return the result
return ans;
}
};
int main() {
int V = 6;
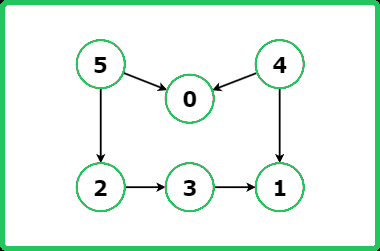
vector<int> adj[V] = {
{},
{},
{3},
{1},
{0,1},
{0,2}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to return the
topological sorting of given graph */
vector<int> ans = sol.topoSort(V, adj);
// Output
cout << "The topological sorting of the given graph is: \n";
for(int i=0; i < V; i++) {
cout << ans[i] << " ";
}
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485
import java.util.*;
class Solution {
// Function to perform DFS traversal
private void dfs(int node, List<Integer> adj[],
int[] vis, Stack<Integer> st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all the neighbors
for (int it : adj[node]) {
// If not visited, recursively perform DFS.
if (vis[it] == 0) {
dfs(it, adj, vis, st);
}
}
/* Add the current node to stack
once all the nodes connected to it
have been processed */
st.push(node);
}
/* Function to return array containing
vertices in Topological order */
public int[] topoSort(int V, List<Integer> adj[]) {
// To store the result
int[] ans = new int[V];
/* Stack to store processed
nodes in reverse order */
Stack<Integer> st = new Stack<>();
// Visited array
int[] vis = new int[V];
// Traverse the graph
for (int i = 0; i < V; i++) {
// Start DFS traversal for unvisited node
if (vis[i] == 0) {
dfs(i, adj, vis, st);
}
}
// Until the stack is empty
for (int i = 0; i < V; i++) {
// Add the top of stack to result
ans[i] = st.pop();
}
// Return the result
return ans;
}
}
class Main {
public static void main(String[] args) {
int V = 6;
List<Integer> adj[] = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
adj[2].add(3);
adj[3].add(1);
adj[4].add(0);
adj[4].add(1);
adj[5].add(0);
adj[5].add(2);
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to return the
topological sorting of given graph */
int[] ans = sol.topoSort(V, adj);
// Output
System.out.println("The topological sorting of the given graph is:");
for (int i = 0; i < V; i++) {
System.out.print(ans[i] + " ");
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
class Solution:
# Function to perform DFS traversal
def dfs(self, node, adj, vis, st):
# Mark the node as visited
vis[node] = 1
# Traverse all the neighbors
for it in adj[node]:
# If not visited, recursively perform DFS.
if vis[it] == 0:
self.dfs(it, adj, vis, st)
# Add the current node to stack
# once all the nodes connected to it
# have been processed
st.append(node)
# Function to return list containing
# vertices in Topological order
def topoSort(self, V, adj):
# To store the result
ans = []
# Stack to store processed
# nodes in reverse order
st = []
# Visited array
vis = [0] * V
# Traverse the graph
for i in range(V):
# Start DFS traversal for unvisited node
if vis[i] == 0:
self.dfs(i, adj, vis, st)
# Until the stack is empty
while st:
# Add the top of stack to result
ans.append(st.pop())
# Return the result
return ans
if __name__ == "__main__":
V = 6
adj = [
[],
[],
[3],
[1],
[0, 1],
[0, 2]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to return the
# topological sorting of given graph
ans = sol.topoSort(V, adj)
# Output
print("The topological sorting of the given graph is:")
for i in range(V):
print(ans[i], end=" ")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283
class Solution {
// Function to perform DFS traversal
dfs(node, adj, vis, st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all the neighbors
for (let it of adj[node]) {
// If not visited, recursively perform DFS.
if (vis[it] === 0) this.dfs(it, adj, vis, st);
}
// Add the current node to stack
// once all the nodes connected to it
// have been processed
st.push(node);
}
// Function to return list containing
// vertices in Topological order
topoSort(V, adj) {
// To store the result
let ans = [];
// Stack to store processed
// nodes in reverse order
let st = [];
// Visited array
let vis = new Array(V).fill(0);
// Traverse the graph
for (let i = 0; i < V; i++) {
// Start DFS traversal for unvisited node
if (vis[i] === 0) {
this.dfs(i, adj, vis, st);
}
}
// Until the stack is empty
while (st.length > 0) {
// Add the top of stack to result
ans.push(st.pop());
}
// Return the result
return ans;
}
}
// Main function to test the code
const main = () => {
const V = 6;
const adj = [
[],
[],
[3],
[1],
[0, 1],
[0, 2]
];
// Creating an instance of
// Solution class
const sol = new Solution();
// Function call to return the
// topological sorting of given graph
const ans = sol.topoSort(V, adj);
// Output
console.log("The topological sorting of the given graph is:");
for (let i = 0; i < V; i++) {
console.log(ans[i] + " ");
}
};
// Call the main function
main();