Trapping Rainwater
Stack / Queues
FAQs
Hard
Given an array of non-negative integers, height representing the elevation of ground. Calculate the amount of water that can be trapped after rain.
Examples:
Input: height= [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6
Explanation: As seen from the diagram 1+1+2+1+1=6 unit of water can be trapped
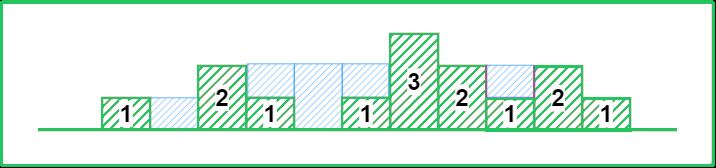
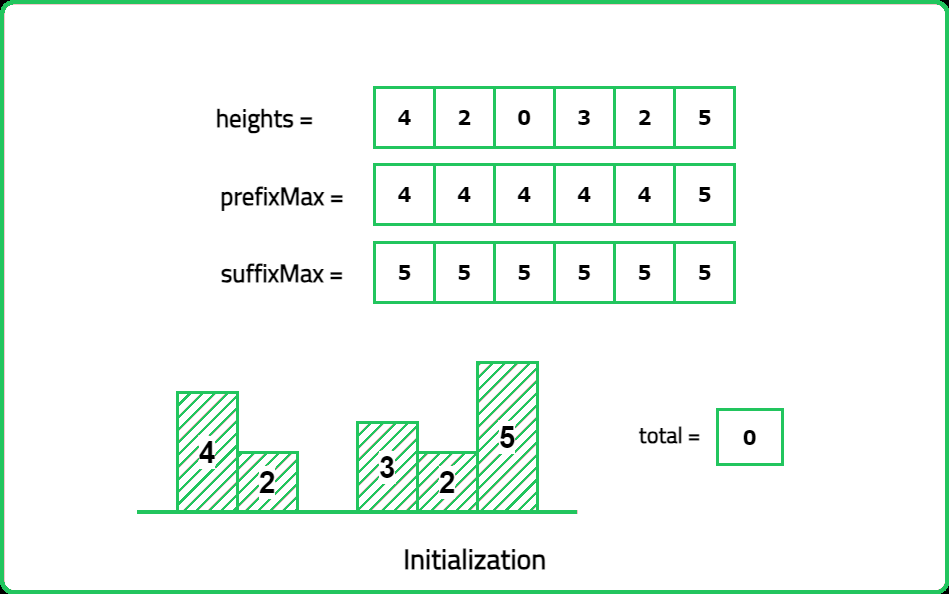
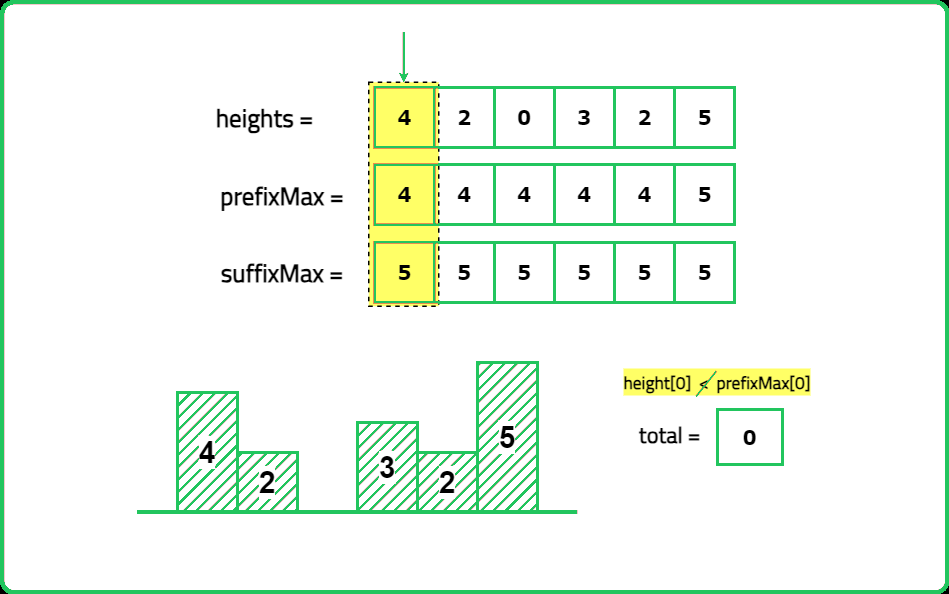
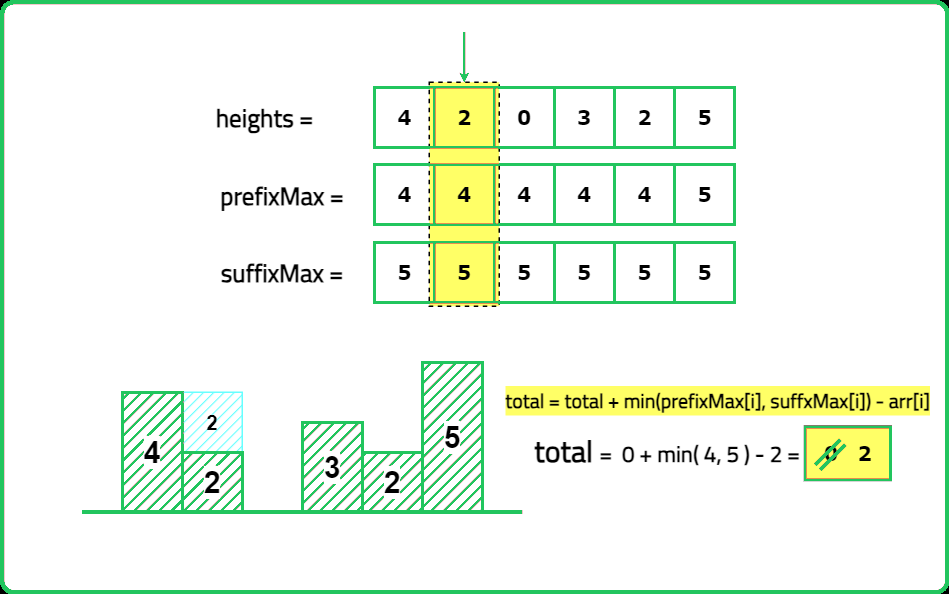
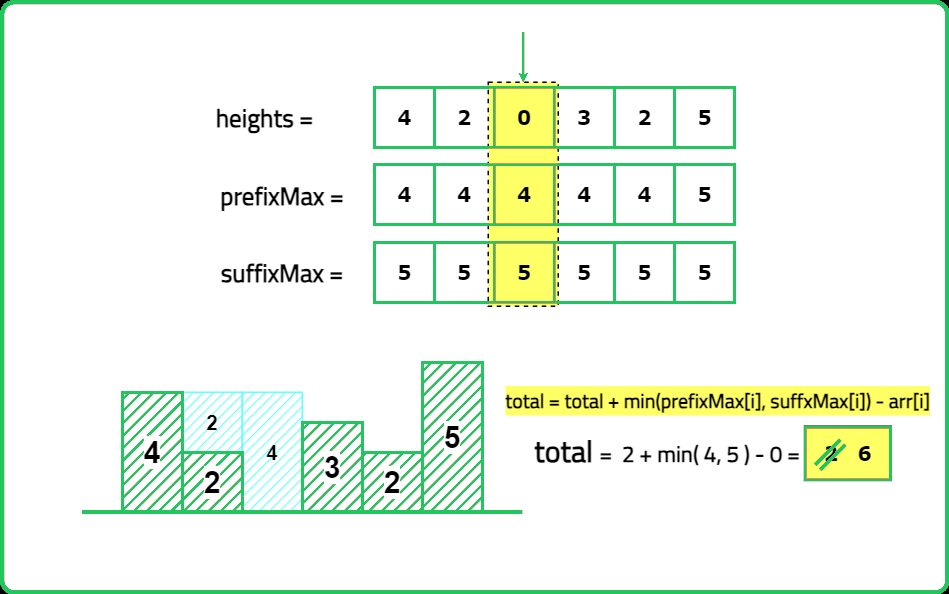
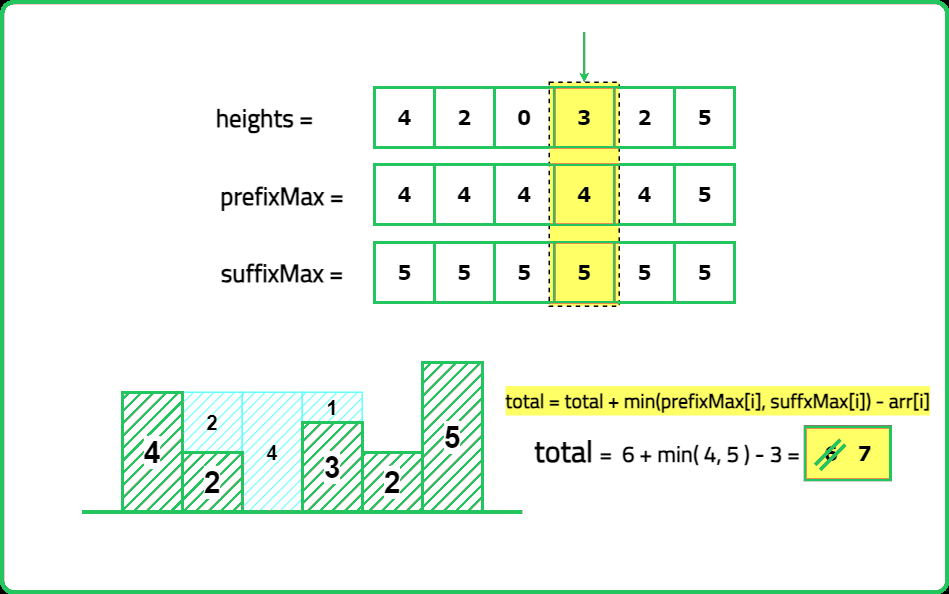
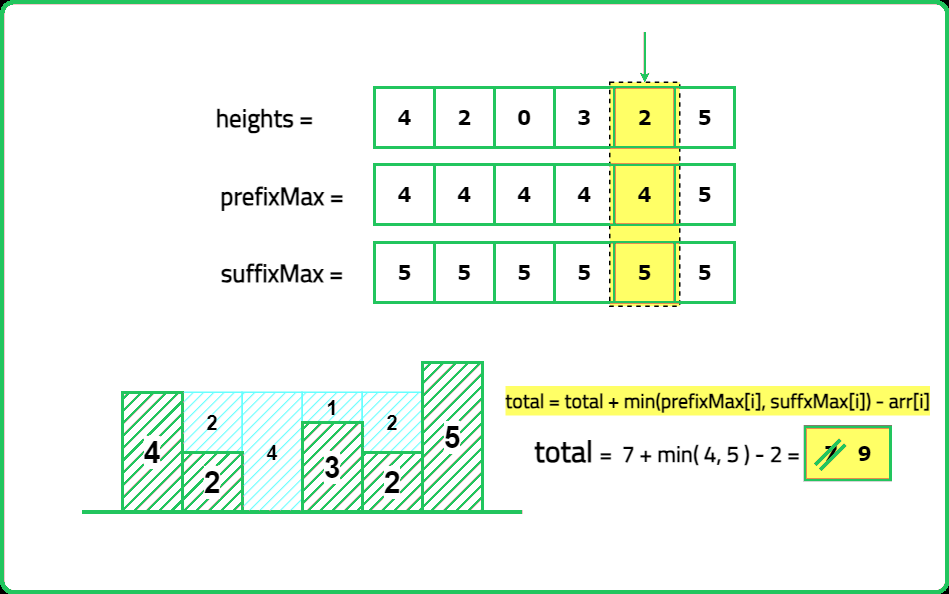
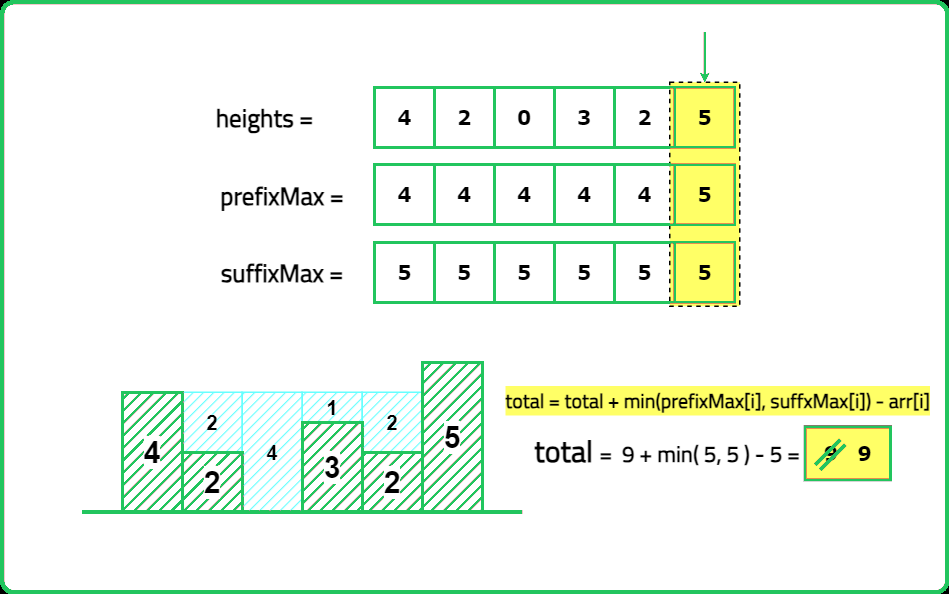
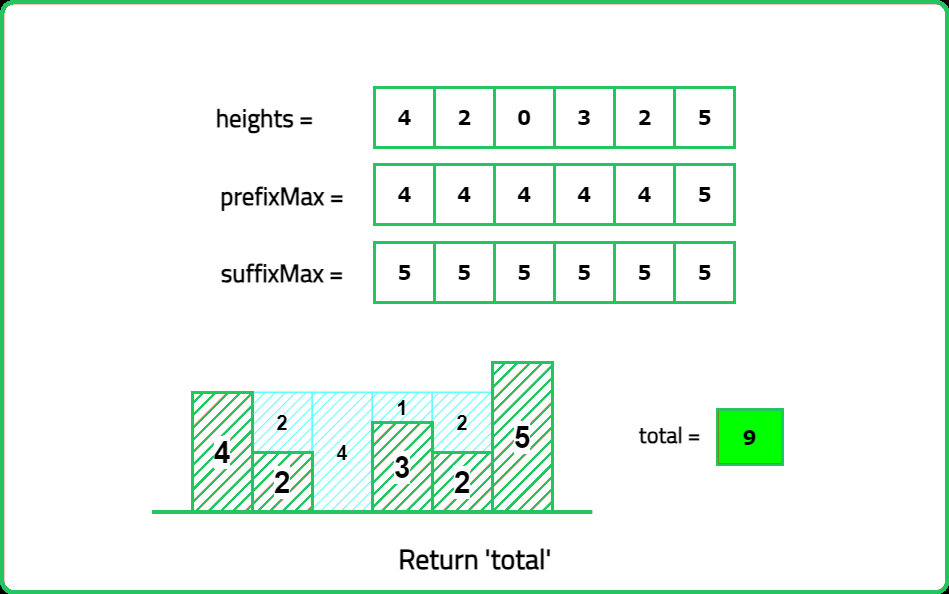
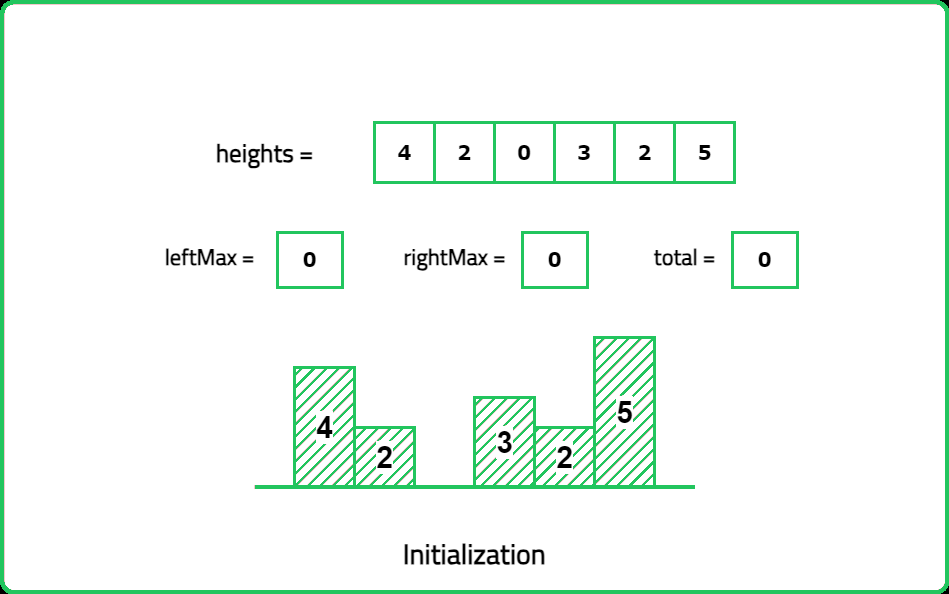
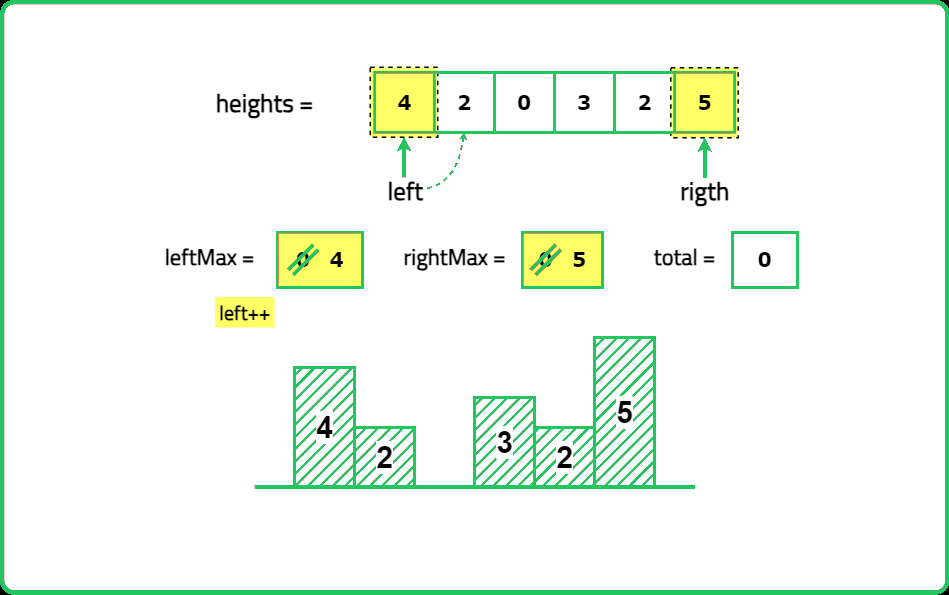
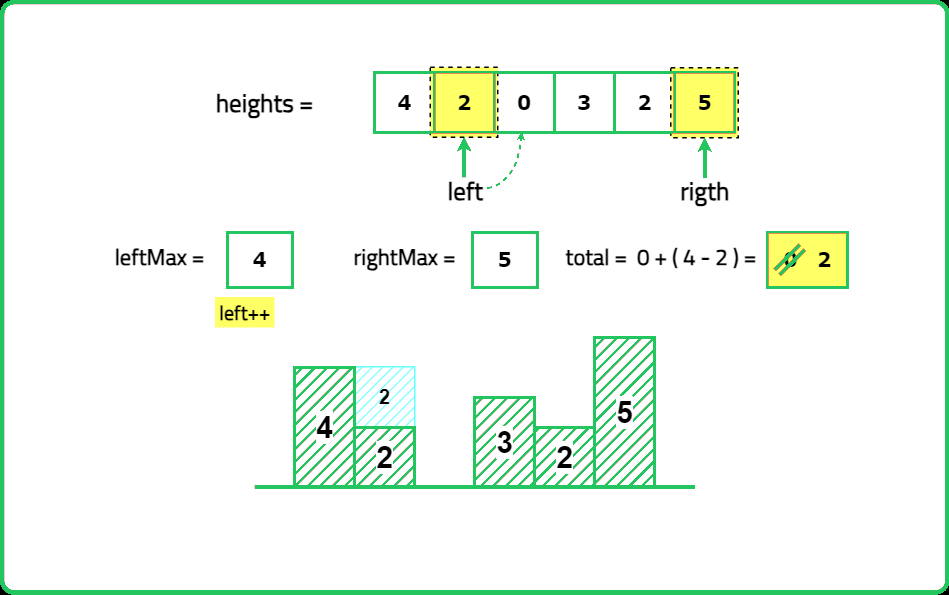
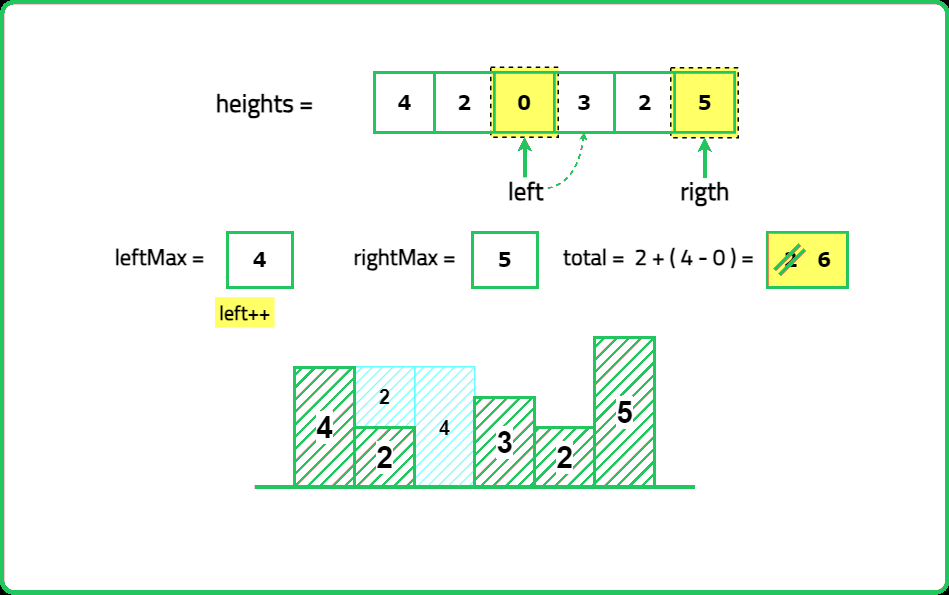
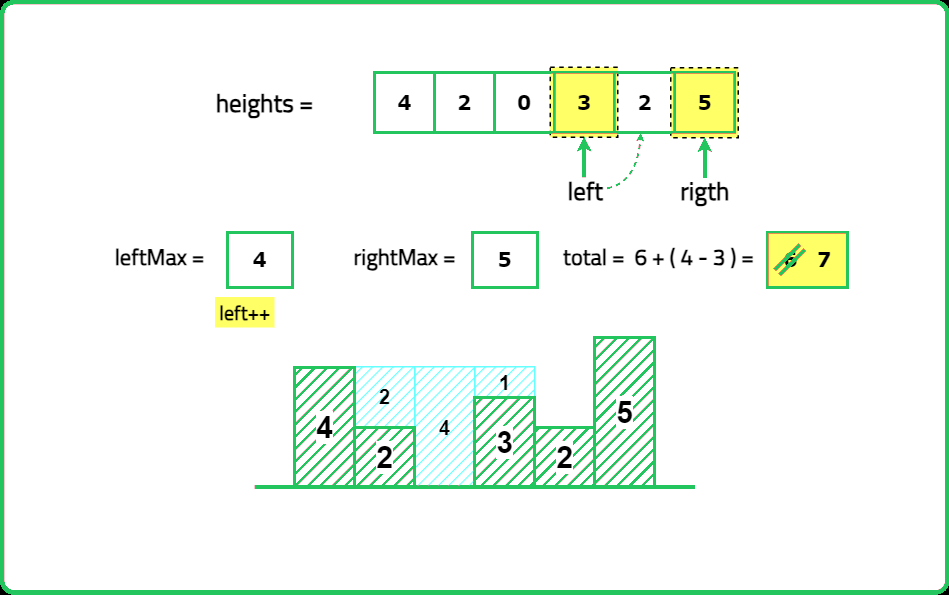
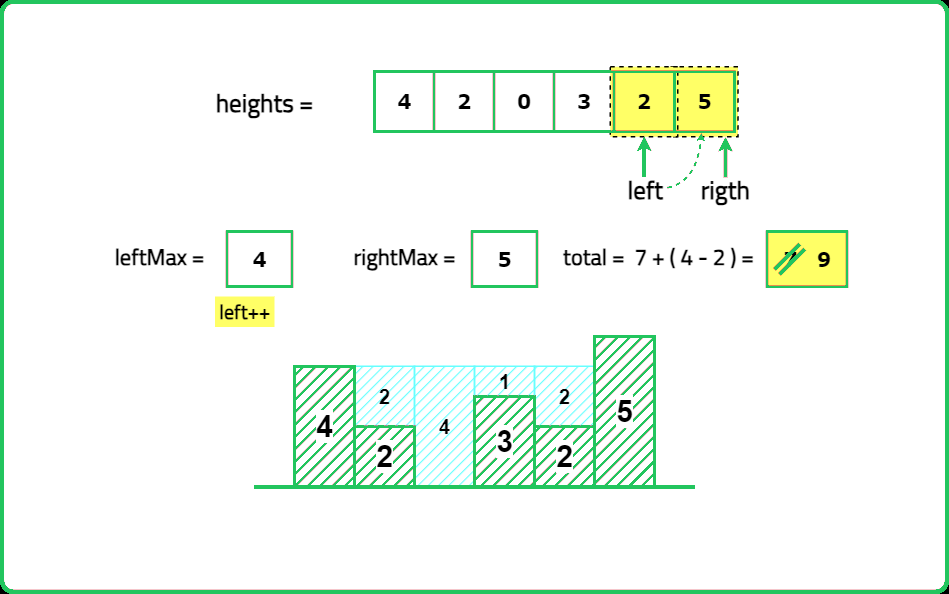
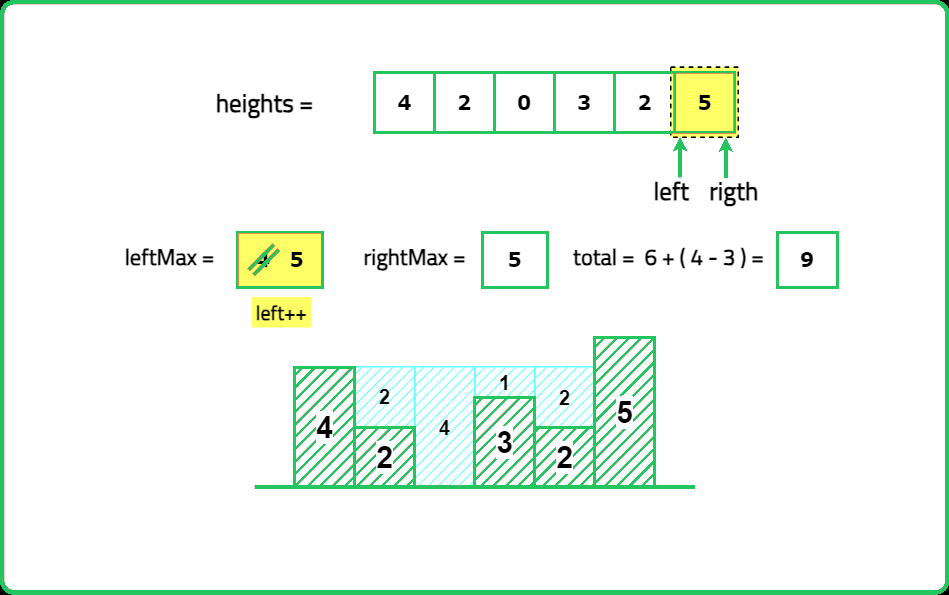
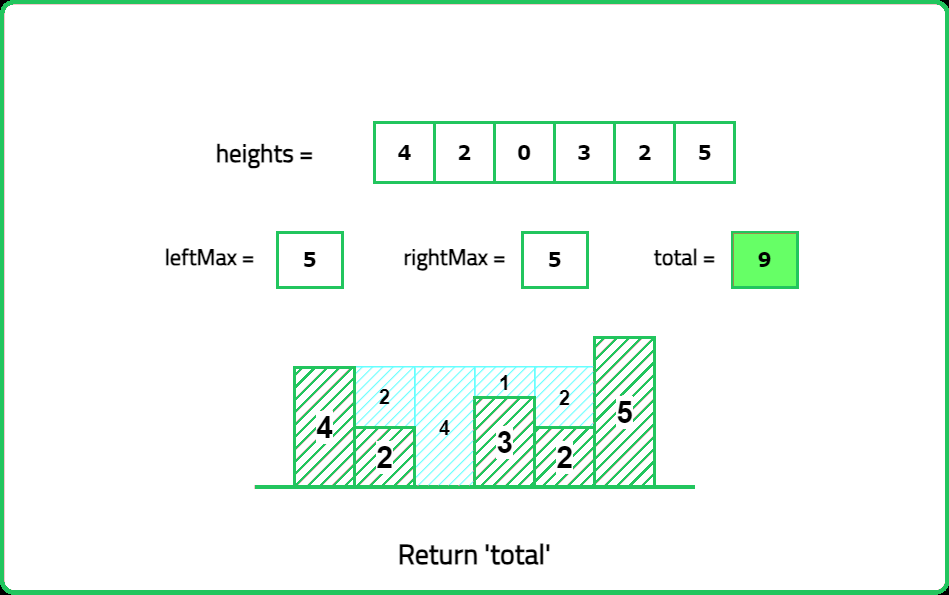
Input: height= [4, 2, 0, 3, 2, 5]
Output: 9
Expalanation: 2+4+1+2=9 unit of water can be trapped
Input: height= [7, 4, 0, 9]
Constraints
- n == height.length
- 1 <= n <= 105
- 0 <= height[i] <= 105
Hints
- Compute left_max[i] → Maximum height from the left up to index i. Compute right_max[i] → Maximum height from the right up to index i. Water trapped at index i is: max(0, min({left_max}[i], {right_max}[i]) - {height}[i])
- Use two pointers (left and right), tracking left_max and right_max. Always process the shorter side first, as it is the limiting factor for trapping water.
Company Tags
HCL Technologies
Activision Blizzard
Flipkart
AMD
JPMorgan Chase
Twilio
OYO Rooms
Cloudflare
Salesforce
Qualcomm
HashiCorp
Snowflake
Epic Games
Target
Bloomberg
Shopify
Nutanix
NVIDIA
Roche
DoorDash
Seagate Technology
Rakuten
Riot Games
ARM
Goldman Sachs
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
Imagine looking at the ground from a side view after a heavy rain. Water gets trapped in the dips and valleys between the heights. To determine the amount of trapped water, it's essential to know the highest barriers to the left and right of each position. These barriers will are important to understand how much water can sit atop each element.
By knowing the maximum heights to the left and right of each position, the water level at that position will be determined by the shorter of these two barriers. The difference between this water level and the height of the ground at that position will give the amount of water trapped there.
Understanding:
Traversing to the left and right side to get the maximum for every height of ground is inefficient. To solve this problem efficiently, two auxiliary arrays will be used to store the maximum heights to the left and right of each position:- Prefix Maximum Array: Stores the maximum of all the elements to the left till the current index.
- Suffix Maximum Array: Stores the maximum of all the elements to the right from the current index.
Approach:
- Store the maximum height from the start to each position in this array. This will help in determining the maximum height to the left of any position.
- Store the maximum height from each position to the end of the array in this array. This will help in determining the maximum height to the right of any position.
- Traverse the array and for each position, determine the water level using the minimum of the prefix and suffix maximum heights. Subtract the ground height at that position from this water level to calculate the trapped water at that position.
- Sum all these values to get the total trapped water.
Dry Run:
Solution:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to find the prefix maximum array
vector<int> findPrefixMax(vector<int> &arr, int &n) {
// To store the prefix maximum
vector<int> prefixMax(n);
// Initial configuration
prefixMax[0] = arr[0];
// Traverse the array
for(int i=1; i < n; i++) {
// Store the maximum till ith index
prefixMax[i] =
max(prefixMax[i-1], arr[i]);
}
// Return the prefix maximum array
return prefixMax;
}
// Function to find the suffix maximum array
vector<int> findSuffixMax(vector<int> &arr, int &n) {
// To store the suffix maximum
vector<int> suffixMax(n);
// Initial configuration
suffixMax[n-1] = arr[n-1];
// Traverse the array
for(int i=n-2; i >= 0; i--) {
// Store the maximum till ith index
suffixMax[i] =
max(suffixMax[i+1], arr[i]);
}
// Return the suffix maximum array
return suffixMax;
}
public:
// Function to get the trapped water
int trap(vector<int> &height){
int n = height.size(); // Size of array
// To store the total trapped rainwater
int total = 0;
// Calculate prefix maximum array
vector<int> leftMax =
findPrefixMax(height, n);
// Calculate suffix maximum array
vector<int> rightMax =
findSuffixMax(height, n);
// Traverse the array
for(int i=0; i < n; i++) {
/* If there are higher grounds
on both side to hold water */
if(height[i] < leftMax[i] &&
height[i] < rightMax[i]) {
// Add up the water on top of current height
total += ( min(leftMax[i], rightMax[i]) -
height[i] );
}
}
// Return the result
return total;
}
};
int main() {
vector<int> heights = {4, 2, 0, 3, 2, 5};
/* Creating an instance of
Solution class */
Solution sol;
// Function call to get the trapped water
int ans = sol.trap(heights);
cout << "The trapped rainwater is: " << ans;
return 0;
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788
import java.util.*;
class Solution {
// Function to find the prefix maximum array
private int[] findPrefixMax(int[] arr, int n) {
// To store the prefix maximum
int[] prefixMax = new int[n];
// Initial configuration
prefixMax[0] = arr[0];
// Traverse the array
for(int i = 1; i < n; i++) {
// Store the maximum till ith index
prefixMax[i] =
Math.max(prefixMax[i-1], arr[i]);
}
// Return the prefix maximum array
return prefixMax;
}
// Function to find the suffix maximum array
private int[] findSuffixMax(int[] arr, int n) {
// To store the suffix maximum
int[] suffixMax = new int[n];
// Initial configuration
suffixMax[n-1] = arr[n-1];
// Traverse the array
for(int i = n-2; i >= 0; i--) {
// Store the maximum till ith index
suffixMax[i] =
Math.max(suffixMax[i+1], arr[i]);
}
// Return the suffix maximum array
return suffixMax;
}
// Function to get the trapped water
public int trap(int[] height) {
int n = height.length; // Size of array
// To store the total trapped rainwater
int total = 0;
// Calculate prefix maximum array
int[] leftMax =
findPrefixMax(height, n);
// Calculate suffix maximum array
int[] rightMax =
findSuffixMax(height, n);
// Traverse the array
for(int i = 0; i < n; i++) {
/* If there are higher grounds
on both side to hold water */
if(height[i] < leftMax[i] &&
height[i] < rightMax[i]) {
// Add up the water on top of current height
total += ( Math.min(leftMax[i], rightMax[i])
- height[i] );
}
}
// Return the result
return total;
}
public static void main(String[] args) {
int[] heights = {4, 2, 0, 3, 2, 5};
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to get the trapped water
int ans = sol.trap(heights);
System.out.println("The trapped rainwater is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980
from typing import List
class Solution:
# Function to find the prefix maximum array
def findPrefixMax(self, arr, n):
# To store the prefix maximum
prefixMax = [0] * n
# Initial configuration
prefixMax[0] = arr[0]
# Traverse the array
for i in range(1, n):
# Store the maximum till ith index
prefixMax[i] = max(prefixMax[i-1], arr[i])
# Return the prefix maximum array
return prefixMax
# Function to find the suffix maximum array
def findSuffixMax(self, arr, n):
# To store the suffix maximum
suffixMax = [0] * n
# Initial configuration
suffixMax[n-1] = arr[n-1]
# Traverse the array
for i in range(n-2, -1, -1):
# Store the maximum till ith index
suffixMax[i] = max(suffixMax[i+1], arr[i])
# Return the suffix maximum array
return suffixMax
# Function to get the trapped water
def trap(self, height):
n = len(height) # Size of array
# To store the total trapped rainwater
total = 0
# Calculate prefix maximum array
leftMax = self.findPrefixMax(height, n)
# Calculate suffix maximum array
rightMax = self.findSuffixMax(height, n)
# Traverse the array
for i in range(n):
# If there are higher grounds
# on both side to hold water
if ( height[i] < leftMax[i] and
height[i] < rightMax[i] ):
# Add up the water on top of current height
total += ( min(leftMax[i], rightMax[i]) -
height[i] )
# Return the result
return total
# Creating an instance of Solution class
sol = Solution()
# Array representing height
heights = [4, 2, 0, 3, 2, 5]
# Function call to get the trapped water
ans = sol.trap(heights)
print("The trapped rainwater is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384
class Solution {
// Function to find the prefix maximum array
findPrefixMax(arr, n) {
// To store the prefix maximum
const prefixMax = new Array(n);
// Initial configuration
prefixMax[0] = arr[0];
// Traverse the array
for (let i = 1; i < n; i++) {
// Store the maximum till ith index
prefixMax[i] =
Math.max(prefixMax[i-1], arr[i]);
}
// Return the prefix maximum array
return prefixMax;
}
// Function to find the suffix maximum array
findSuffixMax(arr, n) {
// To store the suffix maximum
const suffixMax = new Array(n);
// Initial configuration
suffixMax[n-1] = arr[n-1];
// Traverse the array
for (let i = n-2; i >= 0; i--) {
// Store the maximum till ith index
suffixMax[i] =
Math.max(suffixMax[i+1], arr[i]);
}
// Return the suffix maximum array
return suffixMax;
}
// Function to get the trapped water
trap(height) {
const n = height.length; // Size of array
// To store the total trapped rainwater
let total = 0;
// Calculate prefix maximum array
const leftMax = this.findPrefixMax(height, n);
// Calculate suffix maximum array
const rightMax = this.findSuffixMax(height, n);
// Traverse the array
for (let i = 0; i < n; i++) {
/* If there are higher grounds
on both side to hold water */
if (height[i] < leftMax[i] &&
height[i] < rightMax[i]) {
// Add up the water on top of current height
total += ( Math.min(leftMax[i], rightMax[i]) -
height[i] );
}
}
// Return the result
return total;
}
}
// Array representing height
const heights = [4, 2, 0, 3, 2, 5];
// Creating an instance of Solution class
const sol = new Solution();
// Function call to get the trapped water
const ans = sol.trap(heights);
console.log("The trapped rainwater is:", ans);
Complexity Analysis:
Time Complexity: O(N) (where N is the size of given array)
- Calculating the Prefix and Suffix Maximum Arrays take O(N) time each.
- Traversing on the given array once takes O(N) time.
Space Complexity: O(N)
Storing the Prefix and Suffix Maximum Arrays takes O(N) space each.
Intuition:
In earlier solution, storing the prefix and suffix maximums was taking extra space. However, at a particular height, only the minimum height (out of the left maximum height and right maximum height) was considered. This simple means that at a particular moment either the left maximum height or the right maximum height was useful.
Understanding:
It is impossible to find out the left and right barriers beforehand, but a clever way to traverse the array is by traversing it from both ends. The left and right maximum heights (barriers) can be maintained and based on these values the water on top of current height can be calculated using the formula: water = min(leftMax, rightMax) - height,
where height is the height of current ground.
This gives an idea of using two pointers that start from both ends of the array while maintaining the left and right barriers (maximum heights). Since, only the lower barrier (minimum height) is considered, out of the two pointers, only one (having minimum height) will move at a time which ensures that no potential taller height is missed.
Approach:
- Start with two pointers at the beginning and end of the array. Maintain two variables to keep track of the maximum heights encountered so far from both directions.
- Use a loop to move the pointers towards each other until they meet. Compare the heights at the current positions of the pointers.
-
If the height at the left pointer is less than or equal to the height at the right pointer:
- If the current height is less than the maximum height on the left, calculate the water trapped and add to the total.
- Otherwise, update the maximum height on the left. Move the left pointer to the right.
- If the height at the right pointer is less:
- If the current height is less than the maximum height on the right, calculate the water trapped and add to the total.
- Otherwise, update the maximum height on the right. Move the right pointer to the left.
- Once the pointers meet, return the total trapped water.
Dry Run:
Solution:
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to get the trapped water
int trap(vector<int> &height){
int n = height.size(); // Size of array
// To store the total trapped rainwater
int total = 0;
// To store the maximums on both sides
int leftMax = 0, rightMax = 0;
// Left and Right pointers
int left = 0, right = n-1;
// Traverse from both ends
while(left < right) {
// If left height is smaller or equal
if(height[left] <= height[right]) {
// If water can be stored
if(leftMax > height[left]) {
// Update total water
total += leftMax - height[left];
}
// Else update maximum height on left
else leftMax = height[left];
// Shift left by 1
left = left + 1;
}
// Else if right height is smaller
else {
// If water can be stored
if(rightMax > height[right]) {
// Update total water
total += rightMax - height[right];
}
// Else update maximum height on right
else rightMax = height[right];
// Shift right by 1
right = right - 1;
}
}
// Return the result
return total;
}
};
int main() {
vector<int> heights = {4, 2, 0, 3, 2, 5};
/* Creating an instance of
Solution class */
Solution sol;
// Function call to get the trapped water
int ans = sol.trap(heights);
cout << "The trapped rainwater is: " << ans;
return 0;
}1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
import java.util.*;
class Solution {
// Function to get the trapped water
public int trap(int[] height) {
int n = height.length; // Size of array
// To store the total trapped rainwater
int total = 0;
// To store the maximums on both sides
int leftMax = 0, rightMax = 0;
// Left and Right pointers
int left = 0, right = n - 1;
// Traverse from both ends
while (left < right) {
// If left height is smaller or equal
if (height[left] <= height[right]) {
// If water can be stored
if (leftMax > height[left]) {
// Update total water
total += leftMax - height[left];
}
// Else update maximum height on left
else leftMax = height[left];
// Shift left by 1
left = left + 1;
}
// Else if right height is smaller
else {
// If water can be stored
if (rightMax > height[right]) {
// Update total water
total += rightMax - height[right];
}
// Else update maximum height on right
else rightMax = height[right];
// Shift right by 1
right = right - 1;
}
}
// Return the result
return total;
}
public static void main(String[] args) {
int[] heights = {4, 2, 0, 3, 2, 5};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
// Function call to get the trapped water
int ans = sol.trap(heights);
System.out.println("The trapped rainwater is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
class Solution:
# Function to get the trapped water
def trap(self, height):
n = len(height) # Size of array
# To store the total trapped rainwater
total = 0
# To store the maximums on both sides
leftMax = 0
rightMax = 0
# Left and Right pointers
left = 0
right = n - 1
# Traverse from both ends
while left < right:
# If left height is smaller or equal
if height[left] <= height[right]:
# If water can be stored
if leftMax > height[left]:
# Update total water
total += leftMax - height[left]
# Else update maximum height on left
else:
leftMax = height[left]
# Shift left by 1
left += 1
# Else if right height is smaller
else:
# If water can be stored
if rightMax > height[right]:
# Update total water
total += rightMax - height[right]
# Else update maximum height on right
else:
rightMax = height[right]
# Shift right by 1
right -= 1
# Return the result
return total
# Creating an instance of Solution class
sol = Solution()
# Function call to get the trapped water
heights = [4, 2, 0, 3, 2, 5]
ans = sol.trap(heights)
print("The trapped rainwater is:", ans)
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
class Solution {
// Function to get the trapped water
trap(height) {
let n = height.length; // Size of array
// To store the total trapped rainwater
let total = 0;
// To store the maximums on both sides
let leftMax = 0, rightMax = 0;
// Left and Right pointers
let left = 0, right = n - 1;
// Traverse from both ends
while (left < right) {
// If left height is smaller or equal
if (height[left] <= height[right]) {
// If water can be stored
if (leftMax > height[left]) {
// Update total water
total += leftMax - height[left];
}
// Else update maximum height on left
else leftMax = height[left];
// Shift left by 1
left = left + 1;
}
// Else if right height is smaller
else {
// If water can be stored
if (rightMax > height[right]) {
// Update total water
total += rightMax - height[right];
}
// Else update maximum height on right
else rightMax = height[right];
// Shift right by 1
right = right - 1;
}
}
// Return the result
return total;
}
}
// Creating an instance of Solution class
const sol = new Solution();
// Function call to get the trapped water
const heights = [4, 2, 0, 3, 2, 5];
const ans = sol.trap(heights);
console.log("The trapped rainwater is:", ans);
Complexity Analysis:
Time Complexity: O(N) (where N is the size of given array)
The left and right pointers will traverse the whole array in total taking O(N) time.
Space Complexity: O(1)
Using only a couple of variables.
Frequently Occurring Doubts
Q: Why do we take the min(left_max, right_max) for water calculation?
A: Water can only accumulate up to the shortest boundary. If one side is lower, water will overflow, so the shorter height limits trapping.
Q: What happens when height is strictly increasing or decreasing?
A: If strictly increasing, no water is trapped ([1,2,3,4] → 0 water). If strictly decreasing, also no water is trapped ([4,3,2,1] → 0 water). Water is only trapped in a valley shape.
Interview Followup Questions
Q: How would you modify the solution to return the indices where water is trapped?
A: Instead of just summing trapped water, store (index, water_amount) where water > 0.
Q: What if some height[i] values were negative (representing below sea level)?
A: Convert them to absolute depths before applying the same logic.
Notes
Code
✅ Testcase
Input: {'height': '[0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting
Input: {'height': '[4, 2, 0, 3, 2, 5]'}
Expected:
9
9
Actual: -
Time: -
sec
Status: Waiting
Input: {'height': '[7, 4, 0, 9]'}
Expected:
10
10
Actual: -
Time: -
sec
Status: Waiting
Facts
- • This problem, also known as the 'Trapping Rain Water' problem, is a prominent example of issues faced in space optimization
- • This kind of computational approach can be seen in real world applications like cache memory optimization in software applications, or file storage in hard disks where efficient use of space is required
- • Data scientists may also use the concept in analytics software, determining how best to utilize limited memory resources
- • Another practical use is in the gaming industry where such algorithms help in creating realistic water surface phenomena