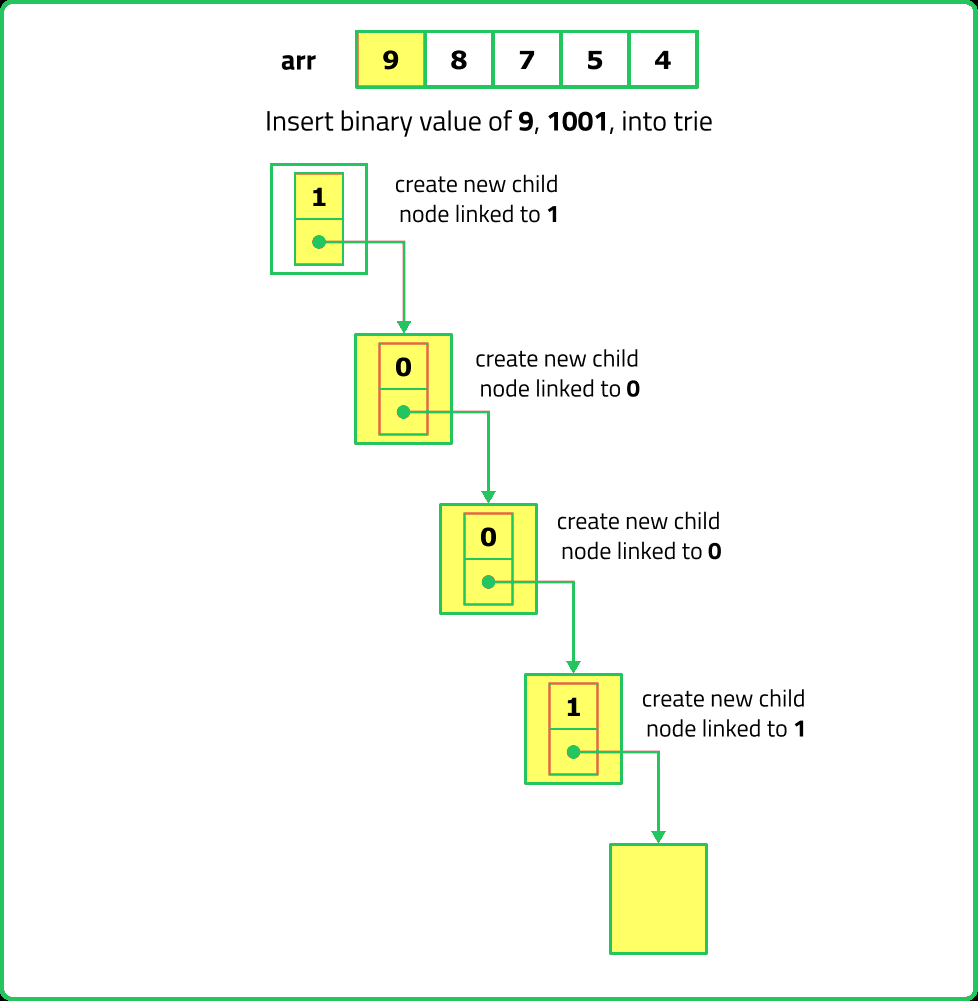
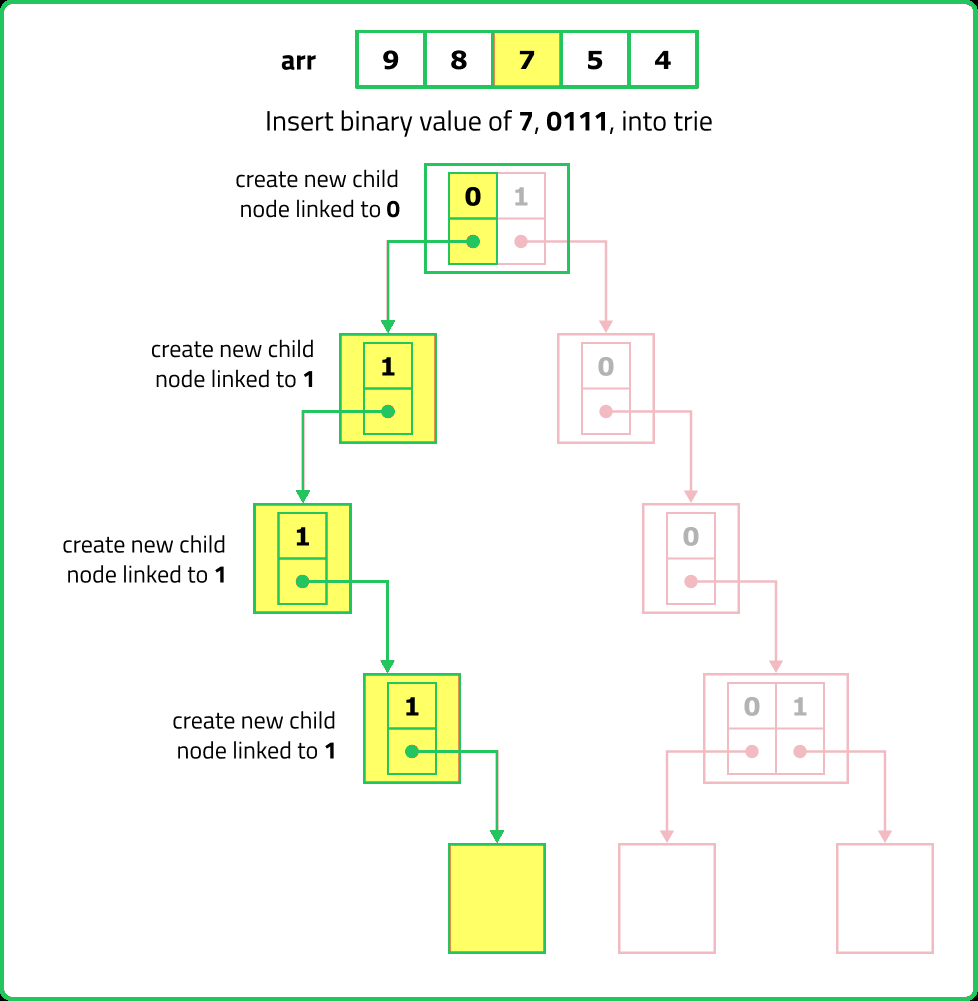
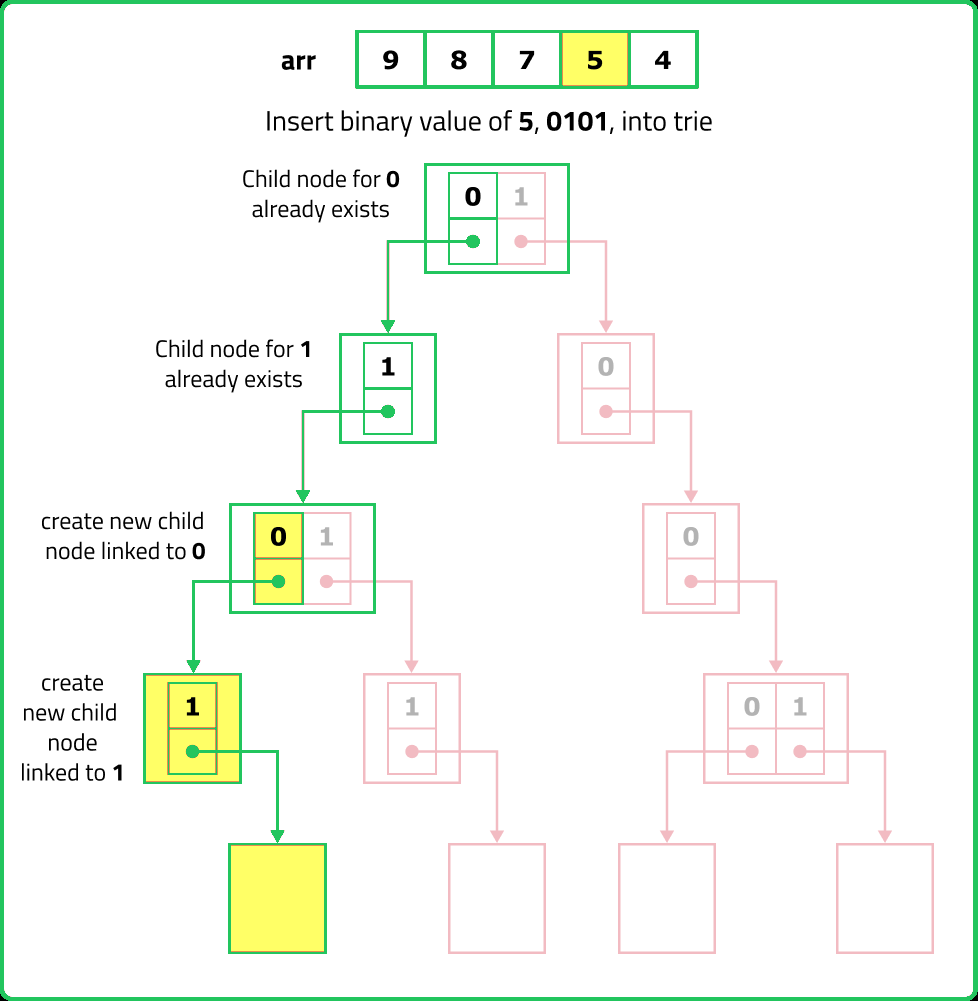
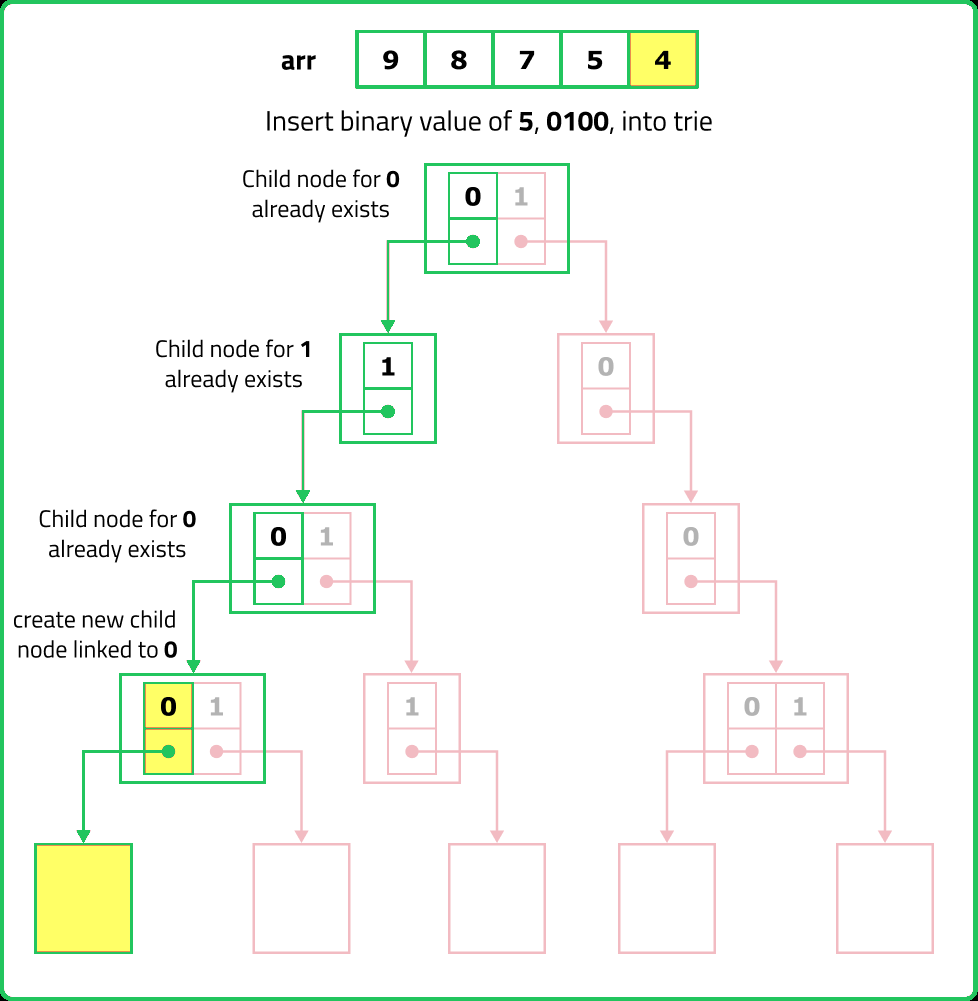
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132
#include <bits/stdc++.h>
using namespace std;
// Node structure for the Trie
struct Node {
Node* links[2];
/*To check if a specific bit
key is present in the child nodes*/
bool containsKey(int bit) {
return (links[bit] != NULL);
}
/*To get child node
corresponding to a
specific bit*/
Node* get(int bit) {
return links[bit];
}
/*To set a child node at a specific
index in the links array*/
void put(int bit, Node* node) {
links[bit] = node;
}
};
// Trie class
class Trie {
private:
Node* root;
public:
// Constructor
Trie() {
root = new Node();
}
// To insert number in Trie
void insert(int num) {
// Start from the root
Node* node = root;
// Iterate each bit
for (int i = 31; i >= 0; i--) {
// Extract i-th bit
int bit = (num >> i) & 1;
/* If the current node doesn't
have a child node with the
current bit*/
if (!node->containsKey(bit)) {
node->put(bit, new Node());
}
node = node->get(bit);
}
}
// Method to find the maximum XOR
int getMax(int num) {
// Start from root
Node* node = root;
// Initialize maximum XOR value
int maxNum = 0;
// Iterate each bit
for (int i = 31; i >= 0; i--) {
// Extract the i-th bit
int bit = (num >> i) & 1;
/*If the complement of the current bit
exists in the Trie update the maximum
XOR value with the current bit
move to the child node corresponding to
the complement of the current bit
Else move to the child node
corresponding to the current bit*/
if (node->containsKey(1 - bit)) {
maxNum |= (1 << i);
node = node->get(1 - bit);
} else {
node = node->get(bit);
}
}
// Return maximum XOR
return maxNum;
}
};
// Solution class
class Solution {
public:
int findMaximumXOR(vector<int>& nums) {
// Create Trie
Trie trie;
// Insert number
for (int num : nums) {
trie.insert(num);
}
// Maximum XOR value
int maxi = 0;
// Iterate each number
for (int num : nums) {
// Update the maximum XOR
maxi = max(maxi, trie.getMax(num));
}
// Return maximum XOR value
return maxi;
}
};
// Main function
int main() {
Solution solution;
// Test case
vector<int> nums = {3, 10, 5, 25, 2, 8};
// Print the input array
cout << "Input: ";
for (int num : nums) {
cout << num << " ";
}
cout << endl;
// Find and print the maximum XOR value
int result = solution.findMaximumXOR(nums);
cout << "Maximum XOR value: " << result << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120
import java.util.*;
class Node {
Node[] links = new Node[2];
// To check if a specific bit key is present in the child nodes
boolean containsKey(int bit) {
return links[bit] != null;
}
// To get the child node corresponding to a specific bit
Node get(int bit) {
return links[bit];
}
// To set a child node at a specific index in the links array
void put(int bit, Node node) {
links[bit] = node;
}
}
// Trie class
class Trie {
private Node root;
// Constructor
Trie() {
root = new Node();
}
// To insert number in Trie
void insert(int num) {
// Start from the root
Node node = root;
// Iterate each bit
for (int i = 31; i >= 0; i--) {
// Extract i-th bit
int bit = (num >> i) & 1;
/* If the current node doesn't
have a child node with the
current bit */
if (!node.containsKey(bit)) {
node.put(bit, new Node());
}
node = node.get(bit);
}
}
// Method to find the maximum XOR
int getMax(int num) {
// Start from root
Node node = root;
// Initialize maximum XOR value
int maxNum = 0;
// Iterate each bit
for (int i = 31; i >= 0; i--) {
// Extract the i-th bit
int bit = (num >> i) & 1;
/*If the complement of the current bit
exists in the Trie update the maximum
XOR value with the current bit
move to the child node corresponding to
the complement of the current bit
Else move to the child node
corresponding to the current bit */
if (node.containsKey(1 - bit)) {
maxNum |= (1 << i);
node = node.get(1 - bit);
} else {
node = node.get(bit);
}
}
// Return maximum XOR
return maxNum;
}
}
// Solution class
class Solution {
public int findMaximumXOR(int[] nums) {
// Create Trie
Trie trie = new Trie();
// Insert number
for (int num : nums) {
trie.insert(num);
}
// Maximum XOR value
int maxi = 0;
// Iterate each number
for (int num : nums) {
// Update the maximum XOR
maxi = Math.max(maxi, trie.getMax(num));
}
// Return maximum XOR value
return maxi;
}
// Main function
public static void main(String[] args) {
Solution solution = new Solution();
// Test case
int[] nums = {3, 10, 5, 25, 2, 8};
// Print the input array
System.out.print("Input: ");
for (int num : nums) {
System.out.print(num + " ");
}
System.out.println();
// Find and print the maximum XOR value
int result = solution.findMaximumXOR(nums);
System.out.println("Maximum XOR value: " + result);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102
class Node:
def __init__(self):
self.links = [None] * 2
# To check if a specific bit
# key is present in the child nodes
def containsKey(self, bit):
return self.links[bit] is not None
# To get the child node
# corresponding to a specific bit
def get(self, bit):
return self.links[bit]
# To set a child node at
# a specific index in the
# links array
def put(self, bit, node):
self.links[bit] = node
# Trie class
class Trie:
def __init__(self):
self.root = Node()
# To insert number in Trie
def insert(self, num):
# Start from the root
node = self.root
# Iterate each bit
for i in range(31, -1, -1):
# Extract i-th bit
bit = (num >> i) & 1
# If the current node doesn't
# have a child node with the
# current bit
if not node.containsKey(bit):
node.put(bit, Node())
node = node.get(bit)
# Method to find the maximum XOR
def getMax(self, num):
# Start from root
node = self.root
# Initialize maximum XOR value
maxNum = 0
# Iterate each bit
for i in range(31, -1, -1):
# Extract the i-th bit
bit = (num >> i) & 1
'''If the complement of the current bit
exists in the Trie update the maximum
XOR value with the current bit
move to the child node corresponding to
the complement of the current bit
Else move to the child node
corresponding to the current bit'''
if node.containsKey(1 - bit):
maxNum |= (1 << i)
node = node.get(1 - bit)
else:
node = node.get(bit)
# Return maximum XOR
return maxNum
# Solution class
class Solution:
def findMaximumXOR(self, nums):
# Create Trie
trie = Trie()
# Insert number
for num in nums:
trie.insert(num)
# Maximum XOR value
maxi = 0
# Iterate each number
for num in nums:
# Update the maximum XOR
maxi = max(maxi, trie.getMax(num))
# Return maximum XOR value
return maxi
# Main function
if __name__ == "__main__":
solution = Solution()
# Test case
nums = [3, 10, 5, 25, 2, 8]
# Print the input array
print("Input:", " ".join(map(str, nums)))
# Find and print the maximum XOR value
result = solution.findMaximumXOR(nums)
print("Maximum XOR value:", result)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117
class Node {
constructor() {
this.links = [null, null];
}
/*To check if a specific
bit key is present in
the child nodes*/
containsKey(bit) {
return this.links[bit] !== null;
}
/* To get the child
node corresponding
to a specific bit*/
get(bit) {
return this.links[bit];
}
/*To set a child node
at a specific index
in the links array*/
put(bit, node) {
this.links[bit] = node;
}
}
// Trie class
class Trie {
constructor() {
this.root = new Node();
}
// To insert number in Trie
insert(num) {
// Start from the root
let node = this.root;
// Iterate each bit
for (let i = 31; i >= 0; i--) {
// Extract i-th bit
const bit = (num >> i) & 1;
/* If the current node doesn't
have a child node with the
current bit */
if (!node.containsKey(bit)) {
node.put(bit, new Node());
}
node = node.get(bit);
}
}
// Method to find the maximum XOR
getMax(num) {
// Start from root
let node = this.root;
// Initialize maximum XOR value
let maxNum = 0;
// Iterate each bit
for (let i = 31; i >= 0; i--) {
// Extract the i-th bit
const bit = (num >> i) & 1;
/*If the complement of the current bit
exists in the Trie update the maximum
XOR value with the current bit
move to the child node corresponding to
the complement of the current bit
Else move to the child node
corresponding to the current bit */
if (node.containsKey(1 - bit)) {
maxNum |= (1 << i);
node = node.get(1 - bit);
} else {
node = node.get(bit);
}
}
// Return maximum XOR
return maxNum;
}
}
// Solution class
class Solution {
findMaximumXOR(nums) {
// Create Trie
const trie = new Trie();
// Insert number
for (const num of nums) {
trie.insert(num);
}
// Maximum XOR value
let maxi = 0;
// Iterate each number
for (const num of nums) {
// Update the maximum XOR
maxi = Math.max(maxi, trie.getMax(num));
}
// Return maximum XOR value
return maxi;
}
}
// Main function
const solution = new Solution();
// Test case
const nums = [3, 10, 5, 25, 2, 8];
// Print the input array
console.log("Input:", nums.join(" "));
// Find and print the maximum XOR value
const result = solution.findMaximumXOR(nums);
console.log("Maximum XOR value:", result);