Count total nodes in a complete BT
Binary Trees
FAQs
Hard
Return the number of nodes in a binary tree given its root.
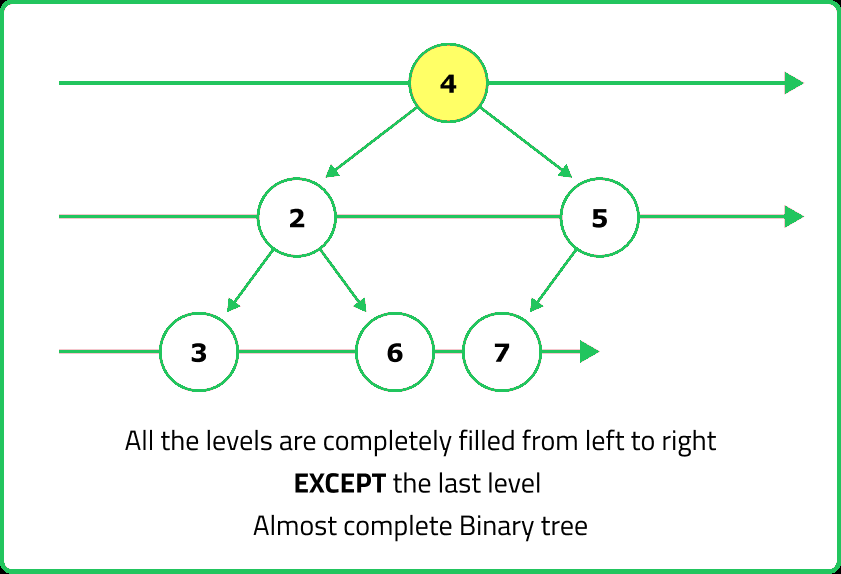
Every level in a complete binary tree possibly with the exception of the final one is fully filled, and every node in the final level is as far to the left as it can be. At the last level h, it can have 1 to 2h nodes inclusive.
Examples:
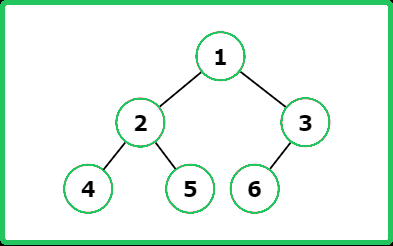
Input : root = [1, 2, 3, 4, 5, 6]
Output : 6
Explanation :
Input : root = [1, 2, 3, 4, 5, 6, 7, 8, 9]
Output : 9
Explanation :
Input : [1, 2, 3]
Constraints
- 1 <= Number of Node <= 5*104
- -105 <= Node.val <= 105
- The tree is guaranteed to be complete.
Hints
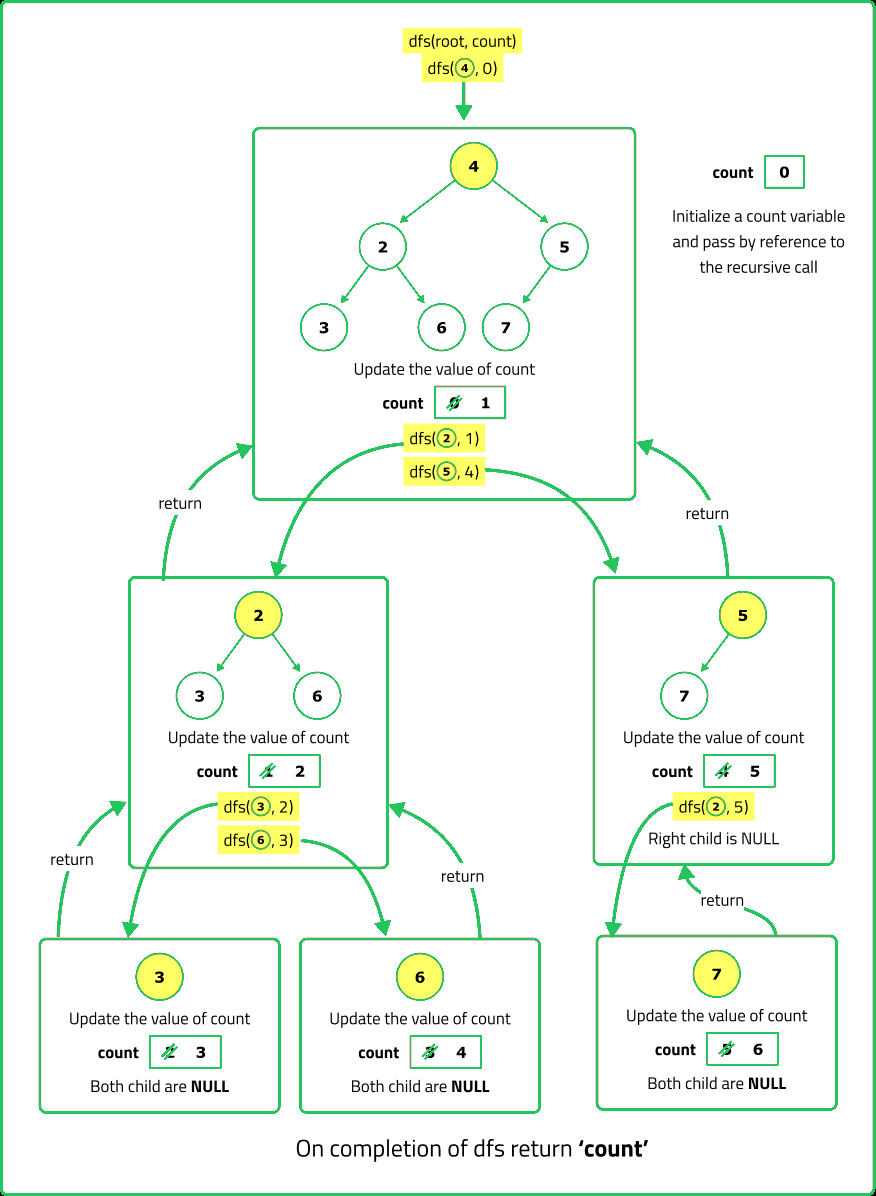
- Perform a DFS (recursive) or BFS (iterative) traversal. Maintain a counter that increments for each node encountered. Base Case: If the root is null, return 0.
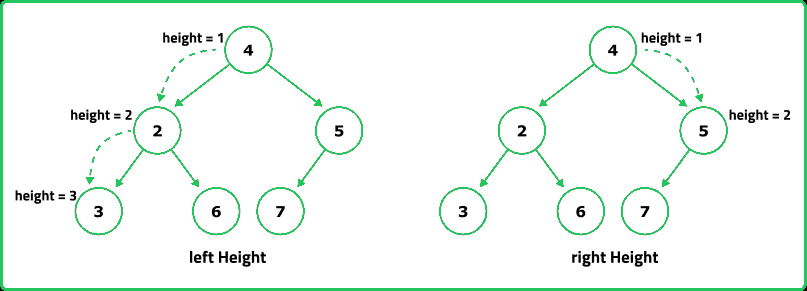
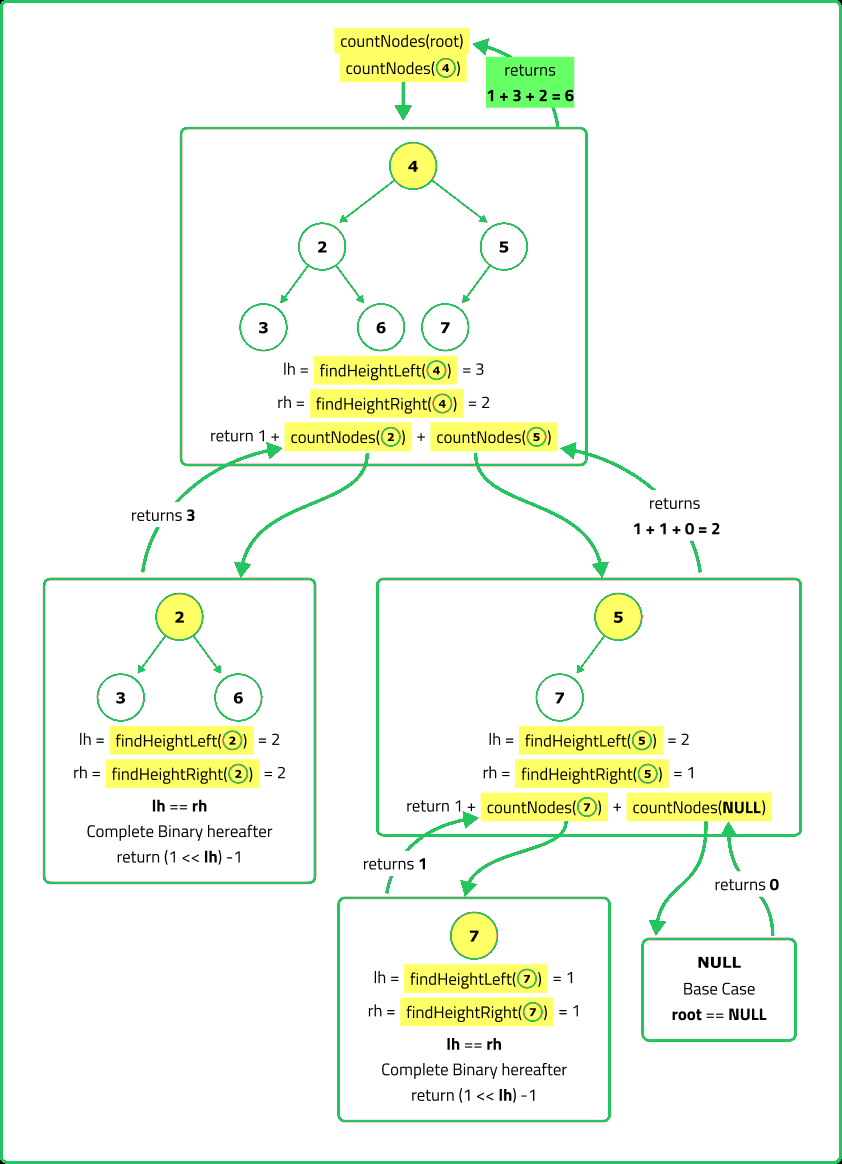
- If a tree is complete, its height can be determined by following the leftmost path. A complete binary tree has at most 2^h - 1 nodes. The last level may not be completely full, meaning we need to count nodes in the last level.
Company Tags
Cerner
Optum
Freshworks
Unity Technologies
Philips Healthcare
HCL Technologies
Goldman Sachs
Shopify
Visa
IBM
Zoho
Instacart
Bloomberg
Broadcom
Pinterest
Medtronic
Rakuten
eBay
Johnson & Johnson
Robinhood
Reddit
Rockstar Games
HashiCorp
Walmart
Dropbox
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition
A complete binary tree is one where every level is fully populated, except possibly for the last level, which is filled from left to right. To determine the total number of nodes in such a tree, a straightforward approach is to use a tree traversal method to count each node. For instance, an inorder traversal method visits nodes in the order of left subtree, current node, and right subtree. By keeping a count and incrementing it each time a node is visited, you can accurately tally the total number of nodes in the tree.
Approach
- Start by setting up a variable to keep track of the total number of nodes in the tree, initializing it to 0.
- **Define a Recursive Inorder Traversal Function:**
- **Base Case:** If the current node is null, return immediately as this signifies that there are no more nodes to process in this path.
- **Recursive Case:** If the current node is not null, first recursively visit the left subtree. After returning from the left subtree, increment the counter by 1 to account for the current node. Then, proceed to recursively visit the right subtree.
- Invoke the recursive inorder traversal function starting from the root of the binary tree. Begin with the counter set to 0.
- After completing the traversal, return the final value of the counter, which now holds the total number of nodes in the binary tree.
Dry Run
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to perform inorder
// traversal and count nodes
void inorder(TreeNode* root, int &count) {
// Base case: If the current
// node is NULL, return
if (root == nullptr) {
return;
}
// Increment count
// for the current node
count++;
// Recursively call inorder
// on the left subtree
inorder(root->left, count);
// Recursively call inorder
// on the right subtree
inorder(root->right, count);
}
// Function to count nodes in the binary tree
int countNodes(TreeNode* root) {
// Base case: If the root is NULL,
// the tree is empty, return 0
if (root == nullptr) {
return 0;
}
// Initialize count variable to
// store the number of nodes
int count = 0;
// Call the inorder traversal
// function to count nodes
inorder(root, count);
// Return the final count of
// nodes in the binary tree
return count;
}
};
int main() {
// Create the binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
Solution sol;
// Call the countNodes function
int totalNodes = sol.countNodes(root);
// Print the result
cout << "Total number of nodes in the Complete Binary Tree: "
<< totalNodes << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
// Definition for a binary tree node.
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
// Function to perform inorder
// traversal and count nodes
public void inorder(TreeNode root, int[] count) {
// Base case: If the current
// node is NULL, return
if (root == null) {
return;
}
// Increment count
// for the current node
count[0]++;
// Recursively call inorder
// on the left subtree
inorder(root.left, count);
// Recursively call inorder
// on the right subtree
inorder(root.right, count);
}
// Function to count nodes in the binary tree
public int countNodes(TreeNode root) {
// Base case: If the root is NULL,
// the tree is empty, return 0
if (root == null) {
return 0;
}
// Initialize count variable to
// store the number of nodes
int[] count = {0};
// Call the inorder traversal
// function to count nodes
inorder(root, count);
// Return the final count of
// nodes in the binary tree
return count[0];
}
}
public class Main {
public static void main(String[] args) {
// Create the binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
Solution sol = new Solution();
// Call the countNodes function
int totalNodes = sol.countNodes(root);
// Print the result
System.out.println("Total number of nodes in the Complete Binary Tree: " + totalNodes);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
# Function to perform inorder
# traversal and count nodes
def inorder(self, root, count):
# Base case: If the current
# node is NULL, return
if root is None:
return
# Increment count
# for the current node
count[0] += 1
# Recursively call inorder
# on the left subtree
self.inorder(root.left, count)
# Recursively call inorder
# on the right subtree
self.inorder(root.right, count)
# Function to count nodes in the binary tree
def count_nodes(self, root):
# Base case: If the root is NULL,
# the tree is empty, return 0
if root is None:
return 0
# Initialize count variable to
# store the number of nodes
count = [0]
# Call the inorder traversal
# function to count nodes
self.inorder(root, count)
# Return the final count of
# nodes in the binary tree
return count[0]
if __name__ == "__main__":
# Create the binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
sol = Solution()
# Call the count_nodes function
total_nodes = sol.count_nodes(root)
# Print the result
print(f"Total number of nodes in the Complete Binary Tree: {total_nodes}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
// Function to perform inorder
// traversal and count nodes
inorder(root, count) {
// Base case: If the current
// node is NULL, return
if (root === null) {
return;
}
// Increment count
// for the current node
count.count++;
// Recursively call inorder
// on the left subtree
this.inorder(root.left, count);
// Recursively call inorder
// on the right subtree
this.inorder(root.right, count);
}
// Function to count nodes in the binary tree
countNodes(root) {
// Base case: If the root is NULL,
// the tree is empty, return 0
if (root === null) {
return 0;
}
// Initialize count variable to
// store the number of nodes
let count = { count: 0 };
// Call the inorder traversal
// function to count nodes
this.inorder(root, count);
// Return the final count of
// nodes in the binary tree
return count.count;
}
}
// Main function
const main = () => {
// Create the binary tree
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
let sol = new Solution();
// Call the countNodes function
let totalNodes = sol.countNodes(root);
// Print the result
console.log(`Total number of nodes in the Complete Binary Tree: ${totalNodes}`);
}
// Call the main function
main();
Complexity Analysis
Time Complexity:O(N) where N is the number of nodes in the binary tree. Each node is visited exactly once, ensuring a linear time complexity.
Space Complexity:O(N) where N is the number of nodes in the binary tree. The recursive stack may use space proportional to the number of nodes, especially in a skewed tree. For a balanced tree, the space complexity is roughly O(log N) as the maximum stack depth corresponds to the tree's height.
Intuition
Given the properties of a complete binary tree, where all levels except possibly the last are fully filled and the nodes on the last level are positioned from left to right, an optimized approach can be employed to determine the number of nodes using the tree's height. The maximum number of nodes in a complete binary tree can be calculated with the formula: (2^h - 1), where (h) is the height. For a perfectly filled last level (perfect binary tree), this formula directly applies. To check if the last level is completely filled, the heights of the left and right subtrees can be compared.
If the heights of the left and right subtrees are equal, it indicates that the last level is filled. If they differ, a recursive approach is used to calculate the nodes in the left and right subtrees and sum them up.
Approach
- Base Case: If the current node is null, return 0, indicating there are no nodes to count at this point.
- Recursive Calls: Compute the heights of the left and right subtrees by making recursive calls.
- Check Heights: If the left height is equal to the right height, it indicates that the last level of the tree is completely filled. In this case, you can calculate the total number of nodes using the formula:
(1 << lh) - 1, where << denotes the left shift operator. - Handle Incomplete Last Level: If the left height does not match the right height, it suggests that the last level is not fully populated. Here, you should recursively compute the number of nodes in both the left and right subtrees, and return the total count as
1 + countNodes(root->left) + countNodes(root->right). - Calculate Tree Heights: To determine the height of a subtree, initialize a height variable to 0. Traverse down the left or right side of the tree using a while loop, incrementing the height variable until reaching a leaf node. Return the final computed height.
Dry Run
Solution
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788
#include <bits/stdc++.h>
using namespace std;
// TreeNode structure
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to count nodes
// in a binary tree
int countNodes(TreeNode* root) {
// Base case: If the root
// is NULL, there are no nodes
if (root == nullptr) {
return 0;
}
// Find the left height and
// right height of the tree
int lh = findHeightLeft(root);
int rh = findHeightRight(root);
// Check if the last level
// is completely filled
if (lh == rh) {
// If so, use the formula for
// total nodes in a perfect
// binary tree i.e. 2^h - 1
return (1 << lh) - 1;
}
// If the last level is not completely
// filled, recursively count nodes in
// left and right subtrees
return 1 + countNodes(root->left) + countNodes(root->right);
}
// Function to find the left height of a tree
int findHeightLeft(TreeNode* node) {
int height = 0;
// Traverse left child until
// reaching the leftmost leaf
while (node) {
height++;
node = node->left;
}
return height;
}
// Function to find the right height of a tree
int findHeightRight(TreeNode* node) {
int height = 0;
// Traverse right child until
// reaching the rightmost leaf
while (node) {
height++;
node = node->right;
}
return height;
}
};
int main() {
// Create the binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
Solution sol;
// Call the countNodes function
int totalNodes = sol.countNodes(root);
// Print the result
cout << "Total number of nodes in the Complete Binary Tree: "
<< totalNodes << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798
import java.util.*;
// Definition for a binary tree node.
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
// Function to count nodes
// in a binary tree
public int countNodes(TreeNode root) {
// Base case: If the root
// is NULL, there are no nodes
if (root == null) {
return 0;
}
// Find the left height and
// right height of the tree
int lh = findHeightLeft(root);
int rh = findHeightRight(root);
// Check if the last level
// is completely filled
if (lh == rh) {
// If so, use the formula for
// total nodes in a perfect
// binary tree i.e. 2^h - 1
return (1 << lh) - 1;
}
// If the last level is not completely
// filled, recursively count nodes in
// left and right subtrees
return 1 + countNodes(root.left) + countNodes(root.right);
}
// Function to find the left height of a tree
private int findHeightLeft(TreeNode node) {
int height = 0;
// Traverse left child until
// reaching the leftmost leaf
while (node != null) {
height++;
node = node.left;
}
return height;
}
// Function to find the right height of a tree
private int findHeightRight(TreeNode node) {
int height = 0;
// Traverse right child until
// reaching the rightmost leaf
while (node != null) {
height++;
node = node.right;
}
return height;
}
}
public class Main {
public static void main(String[] args) {
// Create the binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
Solution sol = new Solution();
// Call the countNodes function
int totalNodes = sol.countNodes(root);
// Print the result
System.out.println("Total number of nodes in the Complete Binary Tree: " + totalNodes);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
# Definition for a binary tree node.
class TreeNode (object):
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
# Function to count nodes
# in a binary tree
def count_nodes(self, root):
# Base case: If the root
# is NULL, there are no nodes
if root is None:
return 0
# Find the left height and
# right height of the tree
lh = self.find_height_left(root)
rh = self.find_height_right(root)
# Check if the last level
# is completely filled
if lh == rh:
# If so, use the formula for
# total nodes in a perfect
# binary tree i.e. 2^h - 1
return (1 << lh) - 1
# If the last level is not completely
# filled, recursively count nodes in
# left and right subtrees
return 1 + self.count_nodes(root.left) + self.count_nodes(root.right)
# Function to find the left height of a tree
def find_height_left(self, node):
height = 0
# Traverse left child until
# reaching the leftmost leaf
while node:
height += 1
node = node.left
return height
# Function to find the right height of a tree
def find_height_right(self, node):
height = 0
# Traverse right child until
# reaching the rightmost leaf
while node:
height += 1
node = node.right
return height
if __name__ == "__main__":
# Create the binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
sol = Solution()
# Call the count_nodes function
total_nodes = sol.count_nodes(root)
# Print the result
print(f"Total number of nodes in the Complete Binary Tree: {total_nodes}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
// Function to count nodes
// in a binary tree
countNodes(root) {
// Base case: If the root
// is NULL, there are no nodes
if (root === null) {
return 0;
}
// Find the left height and
// right height of the tree
const lh = this.findHeightLeft(root);
const rh = this.findHeightRight(root);
// Check if the last level
// is completely filled
if (lh === rh) {
// If so, use the formula for
// total nodes in a perfect
// binary tree i.e. 2^h - 1
return (1 << lh) - 1;
}
// If the last level is not completely
// filled, recursively count nodes in
// left and right subtrees
return 1 + this.countNodes(root.left) + this.countNodes(root.right);
}
// Function to find the left height of a tree
findHeightLeft(node) {
let height = 0;
// Traverse left child until
// reaching the leftmost leaf
while (node !== null) {
height++;
node = node.left;
}
return height;
}
// Function to find the right height of a tree
findHeightRight(node) {
let height = 0;
// Traverse right child until
// reaching the rightmost leaf
while (node !== null) {
height++;
node = node.right;
}
return height;
}
}
// Main function
const main = () => {
// Create the binary tree
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
let sol = new Solution();
// Call the countNodes function
let totalNodes = sol.countNodes(root);
// Print the result
console.log(`Total number of nodes in the Complete Binary Tree: ${totalNodes}`);
}
// Call the main function
main();
Complexity Analysis
Time Complexity: O(log N * log N) where N is the number of nodes in the binary tree. Calculating leftHeight and rightHeight each takes O(log N) time. In the worst-case scenario, the recursive calls occur at most log N times, leading to a total time complexity of O(log N * log N).
Space Complexity:O(log N) where N is the number of nodes in the binary tree. The maximum depth of the recursion stack is equal to the tree's height, which is log N for a complete binary tree.
Frequently Occurring Doubts
Q: What if the tree is a perfect binary tree?
A: If a tree is perfect, it has exactly 2^h - 1 nodes, and we can compute it directly in O(1).
Q: Why does following the leftmost path give the tree height?
A: In a complete tree, every level (except the last) is fully filled, so the leftmost path always reaches the maximum height.
Interview Followup Questions
Q: What if we needed to count nodes in a tree where each node has more than two children?
A: The same DFS/BFS approach works, but the optimized binary search method is specific to binary trees.
Q: How does this compare to counting leaf nodes?
A: Counting leaf nodes involves checking if a node has no children, whereas counting all nodes requires traversing the full structure.
Notes
Code
✅ Testcase
Input: {'root': '1 2 3 4 5 6'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting
Input: {'root': '1 2 3 4 5 6 7 8 9'}
Expected:
9
9
Actual: -
Time: -
sec
Status: Waiting
Input: {'root': '1 2 3 null 4'}
Expected:
4
4
Actual: -
Time: -
sec
Status: Waiting
Facts
- • The concept of counting the number of nodes in a binary tree is useful in many software applications
- • For instance, in file systems and databases, Binary Trees (especially Binary Search Trees) are often used for efficient searching and sorting of data
- • Here, the knowledge of total nodes can be used for optimization, load balancing, and in determining how deep the tree is, which is essential while performing operations like adding, deleting, or searching for a node
- • Furthermore, companies like Google use similar principles in their MapReduce programming model to process huge sets of data efficiently