Construct a BST from a preorder traversal
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that it is always possible to find a binary search tree with the given requirements for the given test cases. Note. As there can be many possible correct answers, the compiler outputs true if the solution is correct, else false.
Examples:
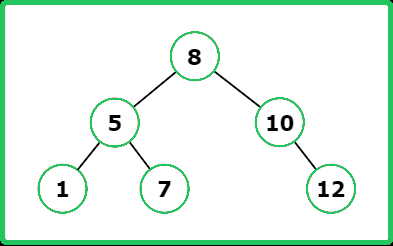
Input : preorder = [8, 5, 1, 7, 10, 12]
Output : [8, 5, 10, 1, 7, null, 12]
Explanation : Below is the BST image
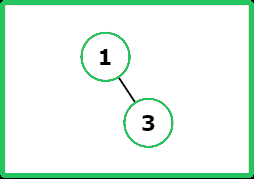
Input : preorder = [1, 3]
Output : [1, null, 3]
Explanation : Below is the BST image
Input : preorder = [5, 3, 2, 4, 6, 7]
Constraints
- 1 <= preorder.length <= 100
- 1 <= preorder[i] <= 1000
- All the values of preorder are unique.
Hints
- "Construct the root using preorder[0]. Recursively divide preorder into left and right subtrees: Elements smaller than root form the left subtree. Elements greater than root form the right subtree. Build the left and right subtrees recursively."
- "Use a monotonic decreasing stack to keep track of parent nodes. Iterate over preorder, and for each value: If it’s smaller than the top of the stack, it’s the left child. If it’s greater, pop elements until finding its parent, then make it the right child."
Company Tags
Editorial
Intuition
To build a Binary Search Tree (BST) from a preorder traversal, it's important to understand how BST properties work with preorder traversal. In a preorder traversal, the root node is visited first, followed by the left subtree, and then the right subtree. This means that the first element in the preorder array is the root of the BST. For the subsequent elements, any number smaller than the root should go to the left subtree, and any number larger should go to the right subtree.
Visualizing this can help: imagine you are planting a tree, and the first seed you plant is the root. Every next seed you plant has to follow the rule: if it's smaller, it goes to the left; if it's larger, it goes to the right. This keeps the tree ordered and balanced.
Approach
- The first element of the preorder array is the root of the BST.
- For each subsequent element in the preorder array, determine its position in the BST based on the following rules:
- If the element is smaller than the root, it goes to the left subtree.
- If the element is larger than the root, it goes to the right subtree.
- Repeat the process for each subtree, treating the current node as the new root and inserting elements to its left or right as appropriate.
Dry Run

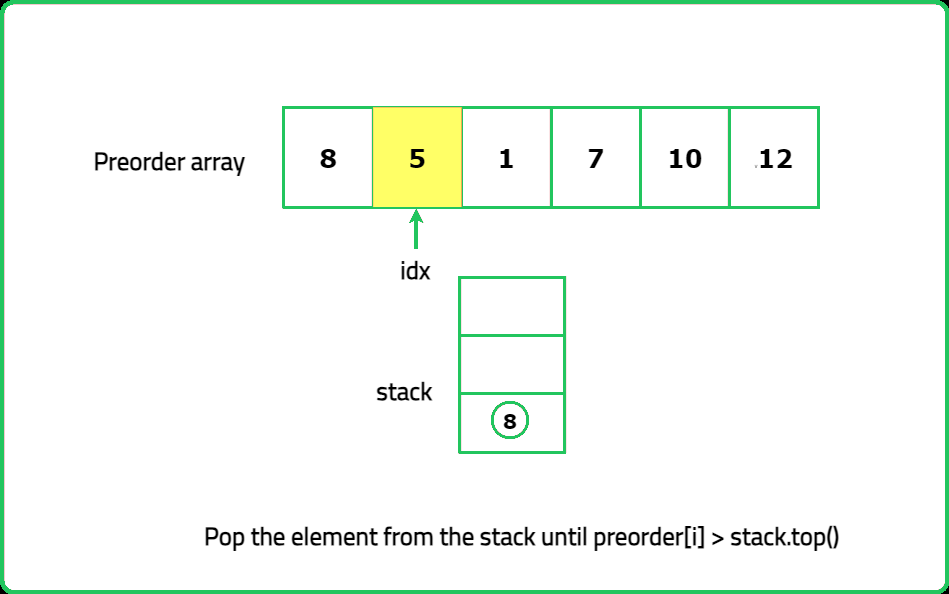
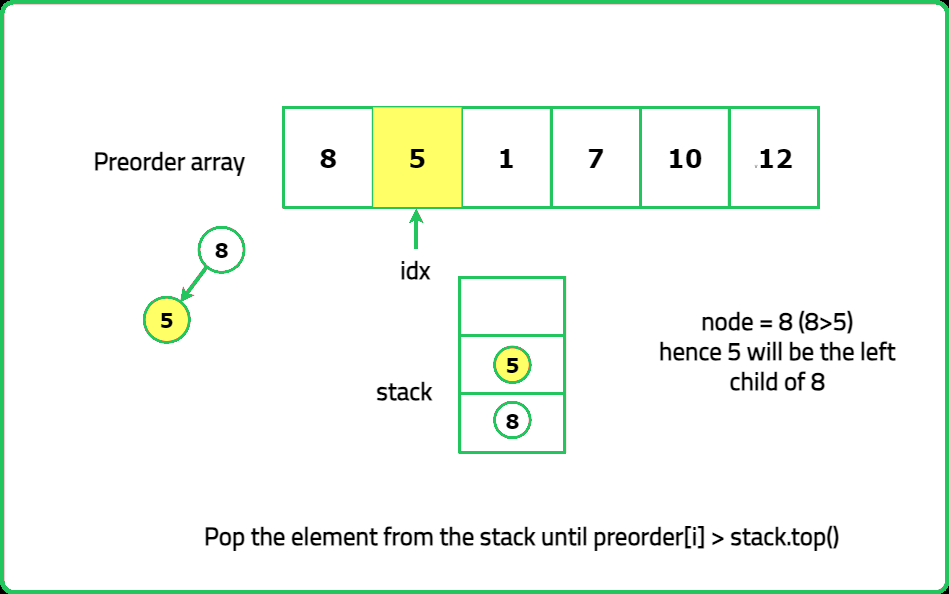
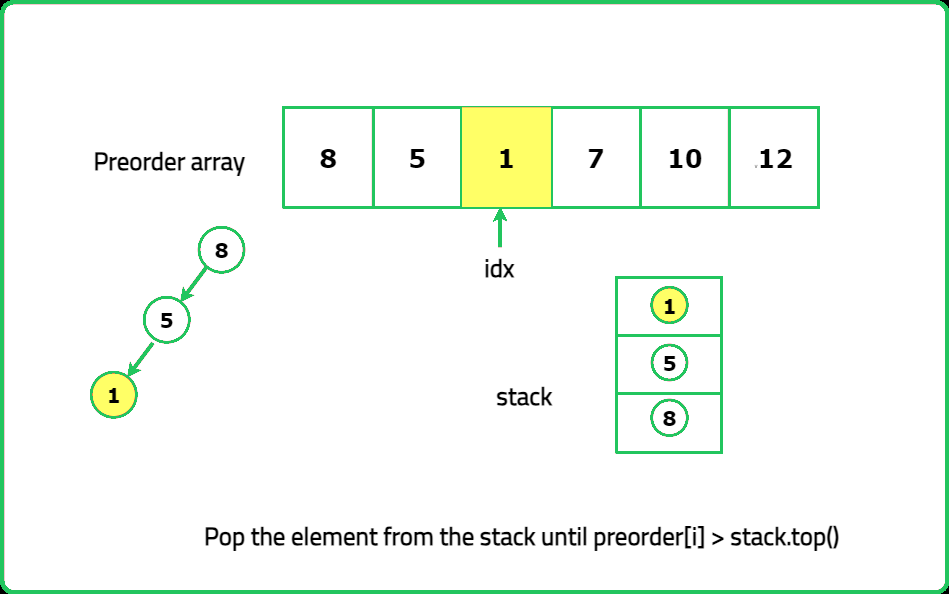
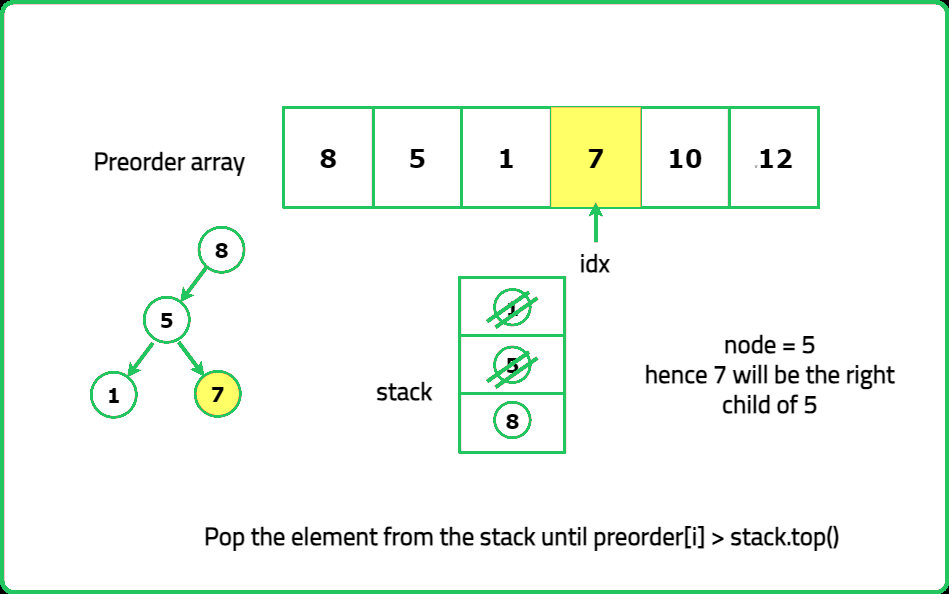
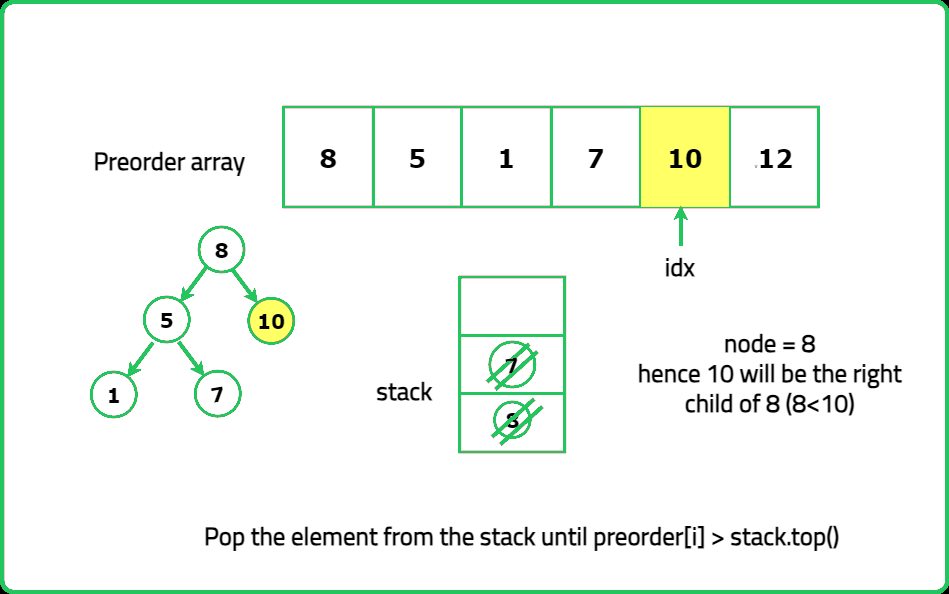
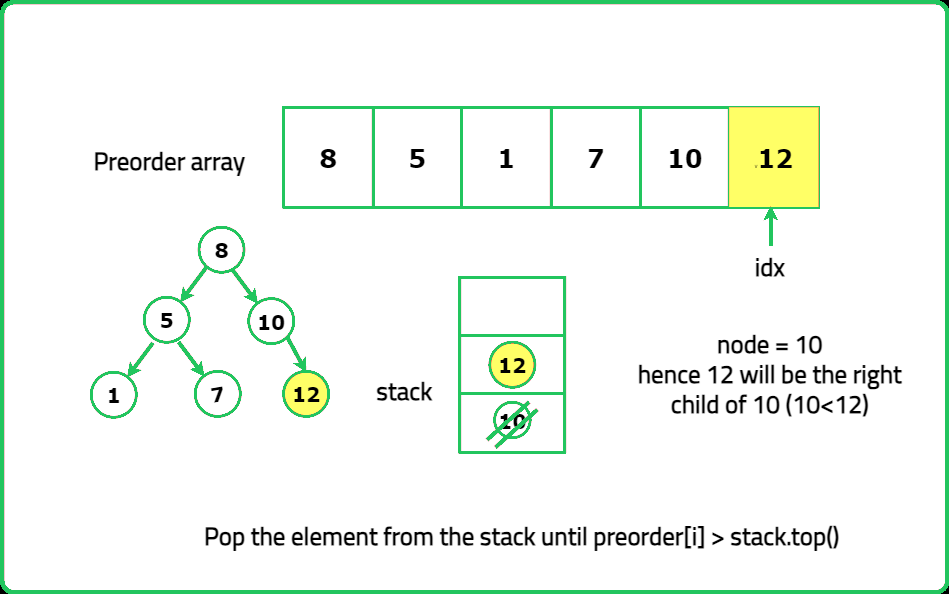
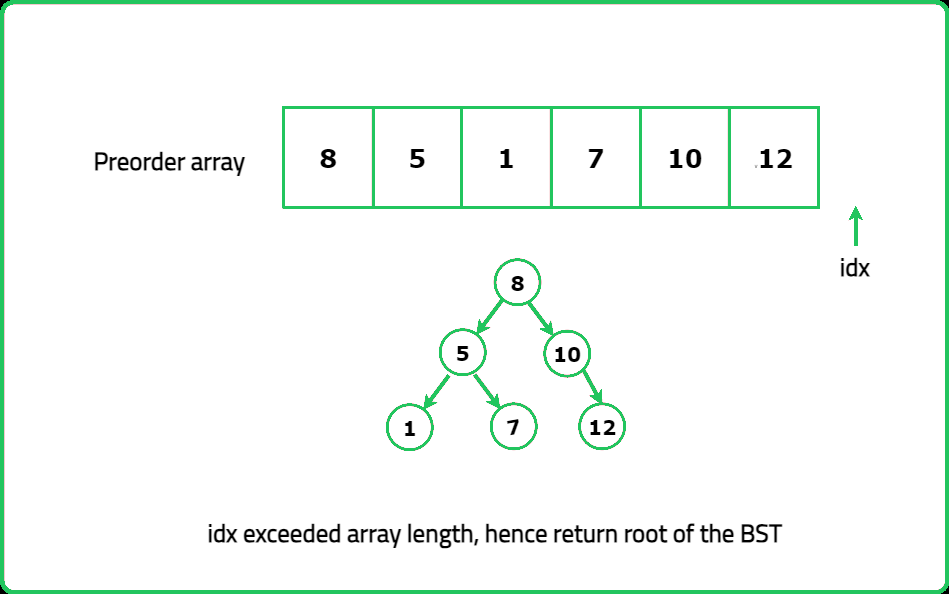








Solution
#include<bits/stdc++.h>
using namespace std;
/**
* Definition for a binary tree node.
*/
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
// Check if the preorder list is empty
if (preorder.empty()) return nullptr;
// The first element is the root
TreeNode* root = new TreeNode(preorder[0]);
stack<TreeNode*> s;
s.push(root);
// Iterate through the rest of the elements
for (int i = 1; i < preorder.size(); ++i) {
TreeNode* node = s.top();
TreeNode* child = new TreeNode(preorder[i]);
// Adjust the stack and place the node in the right position
while (!s.empty() && s.top()->data < preorder[i]) {
node = s.top();
s.pop();
}
// Insert node as left or right child
if (node->data < preorder[i]) {
node->right = child;
} else {
node->left = child;
}
// Push the child node to the stack
s.push(child);
}
return root;
}
};
// Function to print the tree in-order for testing
void inorderTraversal(TreeNode* root) {
if (root != nullptr) {
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
}
int main() {
Solution solution;
vector<int> preorder = {8, 5, 1, 7, 10, 12};
TreeNode* root = solution.bstFromPreorder(preorder);
// Print the constructed BST
inorderTraversal(root);
return 0;
}
import java.util.*;
/**
* Definition for a binary tree node.
*/
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
public TreeNode bstFromPreorder(List<Integer> preorder) {
// Check if the preorder list is empty
if (preorder.isEmpty()) return null;
// The first element is the root
TreeNode root = new TreeNode(preorder.get(0));
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
// Iterate through the rest of the elements
for (int i = 1; i < preorder.size(); i++) {
TreeNode node = stack.peek();
TreeNode child = new TreeNode(preorder.get(i));
// Adjust the stack and place the node in the right position
while (!stack.isEmpty() && stack.peek().data < preorder.get(i)) {
node = stack.pop();
}
// Insert node as left or right child
if (node.data < preorder.get(i)) {
node.right = child;
} else {
node.left = child;
}
// Push the child node to the stack
stack.push(child);
}
return root;
}
// Function to print the tree in-order for testing
public void inorderTraversal(TreeNode root) {
if (root != null) {
inorderTraversal(root.left);
System.out.print(root.data + " ");
inorderTraversal(root.right);
}
}
public static void main(String[] args) {
Solution solution = new Solution();
List<Integer> preorder = Arrays.asList(8, 5, 1, 7, 10, 12);
TreeNode root = solution.bstFromPreorder(preorder);
// Print the constructed BST
solution.inorderTraversal(root);
}
}
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution(object):
def bstFromPreorder(self, preorder):
"""
:type preorder: List[int]
:rtype: TreeNode
"""
# Check if the preorder list is empty
if not preorder:
return None
# The first element is the root
root = TreeNode(preorder[0])
stack = [root]
# Iterate through the rest of the elements
for value in preorder[1:]:
node, child = stack[-1], TreeNode(value)
# Adjust the stack and place the node in the right position
while stack and stack[-1].data < value:
node = stack.pop()
# Insert node as left or right child
if node.data < value:
node.right = child
else:
node.left = child
# Push the child node to the stack
stack.append(child)
return root
# Function to print the tree in-order for testing
def inorderTraversal(self, root):
if root:
self.inorderTraversal(root.left)
print(root.data, end=" ")
self.inorderTraversal(root.right)
# Main method for testing
if __name__ == "__main__":
solution = Solution()
preorder = [8, 5, 1, 7, 10, 12]
root = solution.bstFromPreorder(preorder)
# Print the constructed BST
solution.inorderTraversal(root)
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
bstFromPreorder(preorder) {
// Check if the preorder list is empty
if (!preorder.length) return null;
// The first element is the root
let root = new TreeNode(preorder[0]);
let stack = [root];
// Iterate through the rest of the elements
for (let i = 1; i < preorder.length; i++) {
let node = stack[stack.length - 1];
let child = new TreeNode(preorder[i]);
// Adjust the stack and place the node in the right position
while (stack.length && stack[stack.length - 1].data < preorder[i]) {
node = stack.pop();
}
// Insert node as left or right child
if (node.data < preorder[i]) {
node.right = child;
} else {
node.left = child;
}
// Push the child node to the stack
stack.push(child);
}
return root;
}
}
// Function to print the tree in-order for testing
function inorderTraversal(root) {
if (root !== null) {
inorderTraversal(root.left);
console.log(root.data);
inorderTraversal(root.right);
}
}
// Main method for testing
let solution = new Solution();
let preorder = [8, 5, 1, 7, 10, 12];
let root = solution.bstFromPreorder(preorder);
// Print the constructed BST
inorderTraversal(root);
Complexity Analysis
Time Complexity :The time complexity is O(N * N) as each element is processed once.
Space Complexity :The space complexity is O(N) due to the stack storing nodes.
Pre Requisite : Construct a binary tree from preorder and inorder
Intuition
To build a Binary Search Tree (BST) from a preorder traversal, we need to use the properties of BSTs. In a BST, the left subtree of a node contains only nodes with values less than the node's value, and the right subtree only nodes with values greater than the node's value. The preorder traversal visits nodes in the order: root, left subtree, right subtree. By combining preorder and inorder traversals, we can uniquely determine the structure of the tree.
Approach
- Sort the Preorder Array since the sorted version of the preorder array will give the inorder traversal of the BST.
- With both preorder and inorder arrays, construct the BST by recursively determining the root and its subtrees.
- Recursive Tree Construction: Use a helper function to recursively build the tree:
- If the start indices exceed the end indices, return null.
- The first element in the current preorder range is the root. In the preorder traversal of a binary tree, the root of the tree or subtree is always the first element of the current segment.
- Once the root node is identified, it is necessary to find its position in the inorder array. The inorder traversal provides information about the relative positions of the left and right subtrees. The elements to the left of the root in the inorder array will form the left subtree, while the elements to the right of the root will form the right subtree. This step involves using a map (created from the inorder array) to quickly locate the index of the root element and determine the size of the left subtree.
- Recursively build the left and right subtrees using the determined indices. For the left subtree, we adjust the indices to include only the elements that fall before the root in the inorder array, and similarly for the right subtree, we include only the elements that fall after the root. This recursive process continues until the entire tree is constructed.
Dry Run

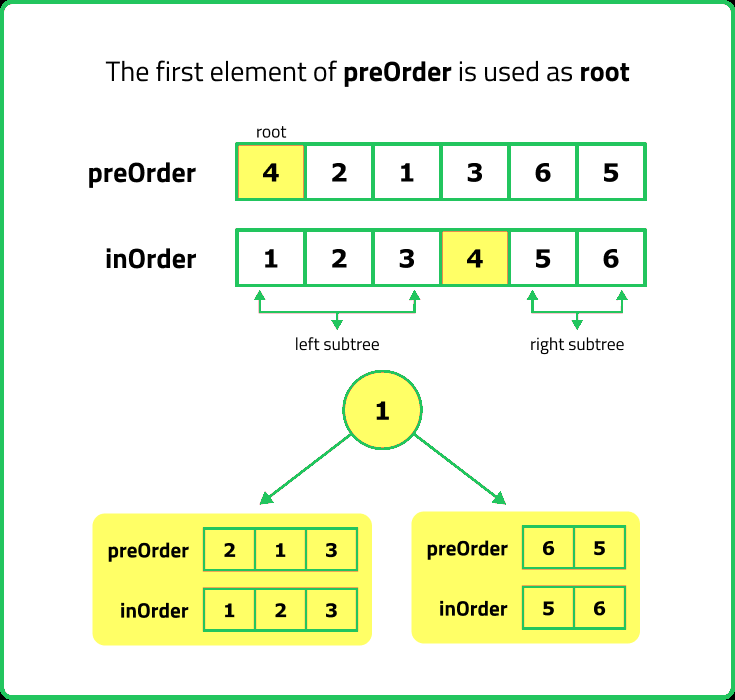
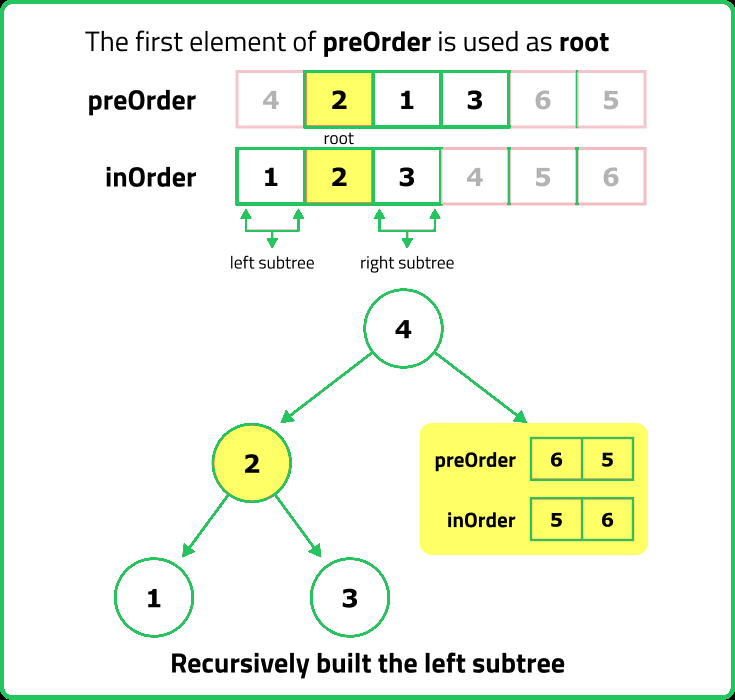
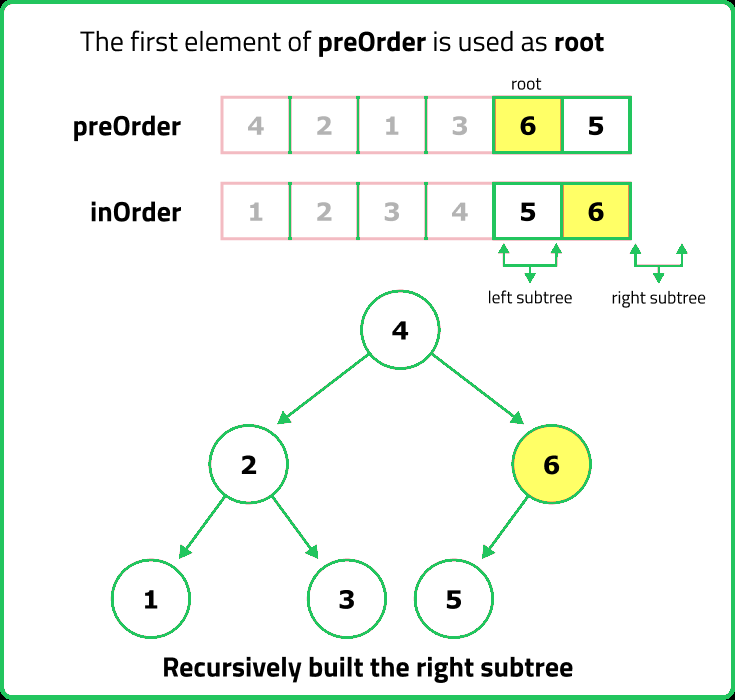




Solution
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
// Convert preorder to inorder by sorting
vector<int> inorder = preorder;
sort(inorder.begin(), inorder.end());
// Create a map to store indices of elements in the inorder traversal
unordered_map<int, int> inMap;
for (int i = 0; i < inorder.size(); ++i) {
inMap[inorder[i]] = i;
}
// Helper function to build the tree
return buildTree(preorder, inMap, 0, preorder.size() - 1, 0, inorder.size() - 1);
}
private:
TreeNode* buildTree(const vector<int>& preorder, unordered_map<int, int>& inMap,
int preStart, int preEnd, int inStart, int inEnd) {
// Base case: if the start indices exceed the end indices, return nullptr
if (preStart > preEnd || inStart > inEnd) return nullptr;
// Create the root node with the value at the current preorder index
TreeNode* root = new TreeNode(preorder[preStart]);
int inRoot = inMap[root->data];
int numsLeft = inRoot - inStart;
// Recursively build the left and right subtrees
root->left = buildTree(preorder, inMap, preStart + 1, preStart + numsLeft, inStart, inRoot - 1);
root->right = buildTree(preorder, inMap, preStart + numsLeft + 1, preEnd, inRoot + 1, inEnd);
return root;
}
};
// Main function for testing
int main() {
Solution sol;
vector<int> preorder = {3, 9, 20, 15, 7};
// Convert preorder to inorder by sorting
vector<int> inorder = preorder;
sort(inorder.begin(), inorder.end());
TreeNode* root = sol.bstFromPreorder(preorder);
// Function to print inorder traversal of the tree (for verification)
function<void(TreeNode*)> printInorder = [&](TreeNode* node) {
if (node) {
printInorder(node->left);
cout << node->data << " ";
printInorder(node->right);
}
};
cout << "Inorder of Unique Binary Tree Created:" << endl;
printInorder(root);
cout << endl;
return 0;
}
import java.util.*;
// Definition for a binary tree node.
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
public TreeNode bstFromPreorder(List<Integer> preorder) {
// Convert preorder to inorder by sorting
List<Integer> inorder = new ArrayList<>(preorder);
Collections.sort(inorder);
// Create a map to store indices of elements in the inorder traversal
Map<Integer, Integer> inMap = new HashMap<>();
for (int i = 0; i < inorder.size(); ++i) {
inMap.put(inorder.get(i), i);
}
// Convert list to array for easier index access
int[] preorderArr = preorder.stream().mapToInt(i -> i).toArray();
// Helper function to build the tree
return buildTree(preorderArr, inMap, 0, preorderArr.length - 1, 0, inorder.size() - 1);
}
private TreeNode buildTree(int[] preorder, Map<Integer, Integer> inMap,
int preStart, int preEnd, int inStart, int inEnd) {
// Base case: if the start indices exceed the end indices, return null
if (preStart > preEnd || inStart > inEnd) return null;
// Create the root node with the value at the current preorder index
TreeNode root = new TreeNode(preorder[preStart]);
int inRoot = inMap.get(root.data);
int numsLeft = inRoot - inStart;
// Recursively build the left and right subtrees
root.left = buildTree(preorder, inMap, preStart + 1, preStart + numsLeft, inStart, inRoot - 1);
root.right = buildTree(preorder, inMap, preStart + numsLeft + 1, preEnd, inRoot + 1, inEnd);
return root;
}
// Main method for testing
public static void main(String[] args) {
Solution sol = new Solution();
List<Integer> preorder = Arrays.asList(3, 9, 20, 15, 7);
// Convert preorder to inorder by sorting
List<Integer> inorder = new ArrayList<>(preorder);
Collections.sort(inorder);
TreeNode root = sol.bstFromPreorder(preorder);
// Function to print inorder traversal of the tree (for verification)
void printInorder(TreeNode node) {
if (node != null) {
printInorder(node.left);
System.out.print(node.data + " ");
printInorder(node.right);
}
}
System.out.println("Inorder of Unique Binary Tree Created:");
printInorder(root);
System.out.println();
}
}
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
def bstFromPreorder(self, preorder):
# Convert preorder to inorder by sorting
inorder = sorted(preorder)
# Create a map to store indices of elements in the inorder traversal
inMap = {val: idx for idx, val in enumerate(inorder)}
# Helper function to build the tree
def buildTree(preStart, preEnd, inStart, inEnd):
# Base case: if the start indices exceed the end indices, return None
if preStart > preEnd or inStart > inEnd:
return None
# Create the root node with the value at the current preorder index
root_val = preorder[preStart]
root = TreeNode(root_val)
inRoot = inMap[root_val]
numsLeft = inRoot - inStart
# Recursively build the left and right subtrees
root.left = buildTree(preStart + 1, preStart + numsLeft, inStart, inRoot - 1)
root.right = buildTree(preStart + numsLeft + 1, preEnd, inRoot + 1, inEnd)
return root
# Call the helper function to build the tree
return buildTree(0, len(preorder) - 1, 0, len(inorder) - 1)
# Main function for testing
if __name__ == "__main__":
sol = Solution()
preorder = [3, 9, 20, 15, 7]
# Convert preorder to inorder by sorting
inorder = sorted(preorder)
root = sol.bstFromPreorder(preorder)
# Function to print inorder traversal of the tree (for verification)
def printInorder(node):
if node:
printInorder(node.left)
print(node.data, end=" ")
printInorder(node.right)
print("Inorder of Unique Binary Tree Created:")
printInorder(root)
print()
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
bstFromPreorder(preorder) {
// Convert preorder to inorder by sorting
const inorder = [...preorder].sort((a, b) => a - b);
// Create a map to store indices of elements in the inorder traversal
const inMap = new Map();
inorder.forEach((val, idx) => inMap.set(val, idx));
// Helper function to build the tree
const buildTree = (preStart, preEnd, inStart, inEnd) => {
// Base case: if the start indices exceed the end indices, return null
if (preStart > preEnd || inStart > inEnd) return null;
// Create the root node with the value at the current preorder index
const rootVal = preorder[preStart];
const root = new TreeNode(rootVal);
const inRoot = inMap.get(rootVal);
const numsLeft = inRoot - inStart;
// Recursively build the left and right subtrees
root.left = buildTree(preStart + 1, preStart + numsLeft, inStart, inRoot - 1);
root.right = buildTree(preStart + numsLeft + 1, preEnd, inRoot + 1, inEnd);
return root;
};
// Call the helper function to build the tree
return buildTree(0, preorder.length - 1, 0, inorder.length - 1);
}
}
// Main function for testing
const main = () => {
const sol = new Solution();
const preorder = [3, 9, 20, 15, 7];
// Convert preorder to inorder by sorting
const inorder = [...preorder].sort((a, b) => a - b);
const root = sol.bstFromPreorder(preorder);
// Function to print inorder traversal of the tree (for verification)
const printInorder = (node) => {
if (node) {
printInorder(node.left);
process.stdout.write(node.data + " ");
printInorder(node.right);
}
};
console.log("Inorder of Unique Binary Tree Created:");
printInorder(root);
console.log();
};
main();
Complexity Analysis
Time Complexity : O(N log N) due to sorting and O(N) for tree construction.
Space Complexity : O(N) for the inorder list and the recursion stack.
Pre Requisite : Check is a tree is BST or not
Building Intuition
To solve the problem of constructing a Binary Search Tree (BST) from a preorder traversal, it is essential to understand the properties of BSTs and the nature of preorder traversal. The key steps involve identifying the root, and then recursively constructing the left and right subtrees within the bounds defined by the BST properties. The first element in the preorder traversal list is always the root of the BST. Elements that appear after the root in the preorder list and are smaller than the root belong to the left subtree. Elements that appear after the root and are greater than the root belong to the right subtree. Recursively apply this logic to construct the entire BST.
The thought process involves recognizing that the preorder traversal provides a natural order to build the tree and using the BST properties to maintain the structure. To proceed first determine the range for constructing the subtrees maintaining an upper bound. For the left subtree, the upper bound is the value of the root, and for the right subtree, the upper bound remains the same as the initial one. This ensures that each subtree respects the BST property where left children are smaller than the root and right children are greater.
Approach
- Initialize an index pointer starting at the beginning of the preorder list.
- Define a recursive function that constructs the BST by taking the current index, the preorder list, and an upper bound as parameters.
- If the current index exceeds the length of the preorder list or the current element exceeds the upper bound, return null.
- Create a new tree node with the current element and increment the index.
- Recursively construct the left subtree with the updated index and the current element as the new upper bound.
- Recursively construct the right subtree with the updated index and the original upper bound.
- Return the constructed tree node.
Dry Run

Solution
#include<bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
// Start the recursive function with the first element as the root
// and the entire range of valid numbers
int index = 0; // Initialize index
return bstFromPreorderHelper(preorder, INT_MAX, index);
}
private:
TreeNode* bstFromPreorderHelper(vector<int>& preorder, int bound, int& index) {
// If all elements are used or the next element
// is greater than the bound, return null
if (index == preorder.size() || preorder[index] > bound) return nullptr;
// Create a new TreeNode with the current value
TreeNode* root = new TreeNode(preorder[index++]);
// Recursively construct the left subtree
// with the current value as the new bound
root->left = bstFromPreorderHelper(preorder, root->data, index);
// Recursively construct the right subtree
// with the same bound as the parent's bound
root->right = bstFromPreorderHelper(preorder, bound, index);
// Return the constructed subtree's root
return root;
}
};
// Example usage
int main() {
Solution solution;
vector<int> preorder = {8, 5, 1, 7, 10, 12};
TreeNode* bst = solution.bstFromPreorder(preorder);
// Add code to print or use the bst as needed
return 0;
}import java.util.*;
// Definition for a binary tree node.
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) { data = val; left = null; right = null; }
}
class Solution {
public TreeNode bstFromPreorder(List<Integer> preorder) {
// Start the recursive function
// with the first element as the root
// and the entire range of valid numbers
return bstFromPreorderHelper(preorder, Integer.MAX_VALUE, new int[]{0});
}
private TreeNode bstFromPreorderHelper(List<Integer> preorder, int bound, int[] index) {
// If all elements are used or the next element
// is greater than the bound, return null
if (index[0] == preorder.size() || preorder.get(index[0]) > bound) return null;
// Create a new TreeNode with the current value
TreeNode root = new TreeNode(preorder.get(index[0]++));
// Recursively construct the left subtree
// with the current value as the new bound
root.left = bstFromPreorderHelper(preorder, root.data, index);
// Recursively construct the right subtree
// with the same bound as the parent's bound
root.right = bstFromPreorderHelper(preorder, bound, index);
// Return the constructed subtree's root
return root;
}
public static void main(String[] args) {
Solution solution = new Solution();
List<Integer> preorder = Arrays.asList(8, 5, 1, 7, 10, 12);
TreeNode bst = solution.bstFromPreorder(preorder);
// Add code to print or use the bst as needed
}
}
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
def bstFromPreorder(self, preorder):
# Start the recursive function
# with the first element as the root
# and the entire range of valid numbers
return self._bstFromPreorderHelper(preorder, float('inf'), [0])
def _bstFromPreorderHelper(self, preorder, bound, index):
# If all elements are used or the next element
# is greater than the bound, return None
if index[0] == len(preorder) or preorder[index[0]] > bound:
return None
# Create a new TreeNode with the current value
root = TreeNode(preorder[index[0]])
index[0] += 1
# Recursively construct the left subtree
# with the current value as the new bound
root.left = self._bstFromPreorderHelper(preorder, root.data, index)
# Recursively construct the right subtree
# with the same bound as the parent's bound
root.right = self._bstFromPreorderHelper(preorder, bound, index)
# Return the constructed subtree's root
return root
# Example usage
if __name__ == "__main__":
solution = Solution()
preorder = [8, 5, 1, 7, 10, 12]
bst = solution.bstFromPreorder(preorder)
# Add code to print or use the bst as needed
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
bstFromPreorder(preorder) {
// Start the recursive function
// with the first element as the root
// and the entire range of valid numbers
return this.bstFromPreorderHelper(preorder, Number.MAX_VALUE, [0]);
}
bstFromPreorderHelper(preorder, bound, index) {
// If all elements are used or the next element
// is greater than the bound, return null
if (index[0] === preorder.length || preorder[index[0]] > bound) return null;
// Create a new TreeNode with the current value
let root = new TreeNode(preorder[index[0]++]);
// Recursively construct the left subtree
// with the current value as the new bound
root.left = this.bstFromPreorderHelper(preorder, root.data, index);
// Recursively construct the right subtree
// with the same bound as the parent's bound
root.right = this.bstFromPreorderHelper(preorder, bound, index);
// Return the constructed subtree's root
return root;
}
}
// Example usage
let solution = new Solution();
let preorder = [8, 5, 1, 7, 10, 12];
let bst = solution.bstFromPreorder(preorder);
console.log(bst);
Complexity Analysis
Time Complexity O(N) due to visiting each node once in the preorder traversal.
SpaceComplexity O(h) where h is the height of the tree due to recursion stack.
Frequently Occurring Doubts
Q: How do we efficiently determine left and right subtrees?
A: The first element greater than root in preorder marks the start of the right subtree.
Q: Can this problem be solved using inorder traversal?
A: No, because inorder traversal does not preserve hierarchy (only sorts elements).
Interview Followup Questions
Q: How would you construct a BST from its postorder traversal?
A: Use reverse traversal (Right → Left → Root) and construct in reverse.
Q: How would you construct a BST from its inorder traversal?
A: Impossible unless we also have preorder/postorder, as inorder does not provide hierarchy.
Notes
Code
true
true
true
Facts
- • Fun Fact: The practical application of this programming problem is most prevalent in the development of databases and search engines
- • Binary Search Trees (BSTs) are extensively used to streamline searching and sorting processes
- • For instance, in a database with millions of records, using BSTs significantly reduces the time complexity to find a specific record
- • Also, the concept of preorder traversal is used in JavaScript frameworks like React to navigate around the Document Object Model (DOM)
- • The knowledge and ability to construct a BST from a given preorder traversal data can help in optimizing tasks related to searching, insertion, and deletion in the real-world software applications