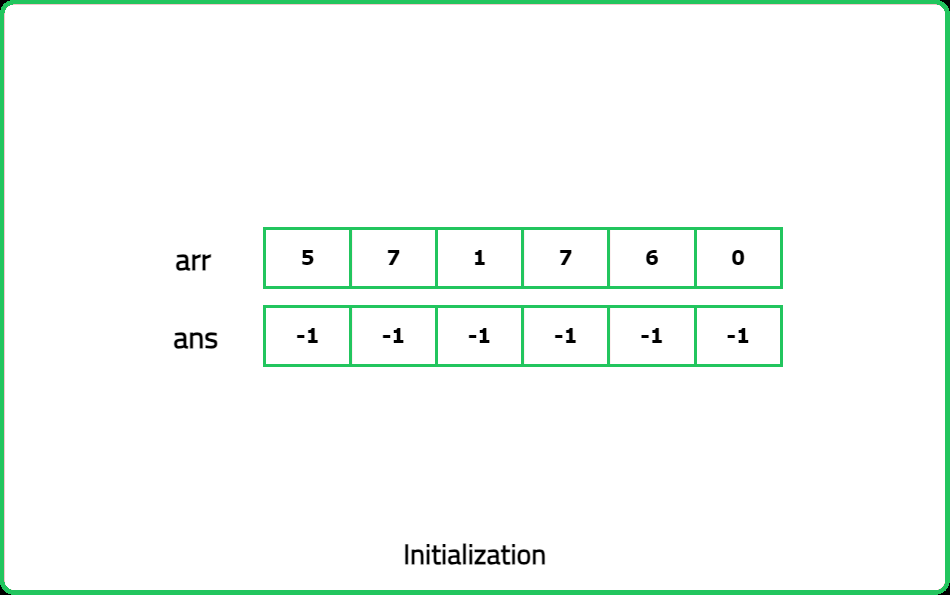
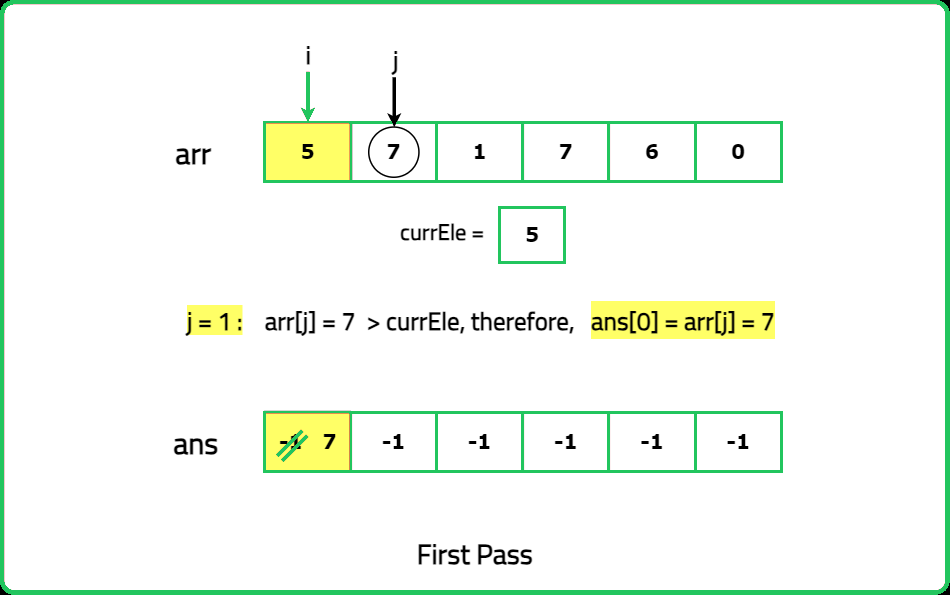
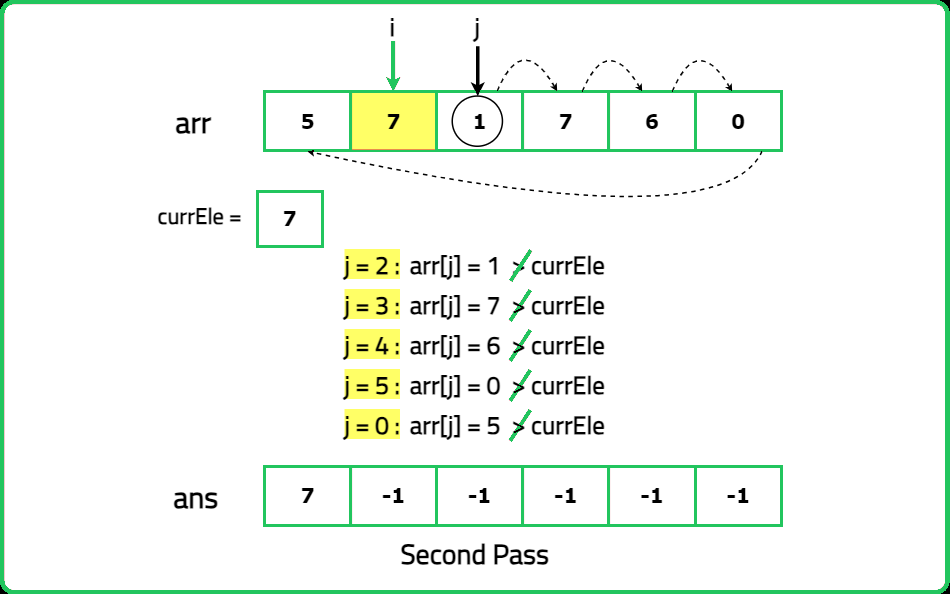
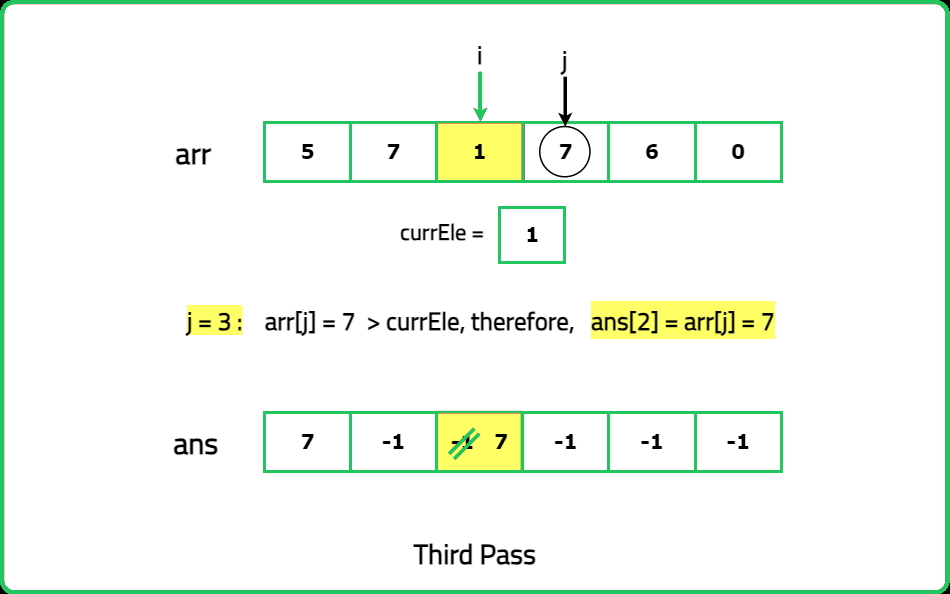
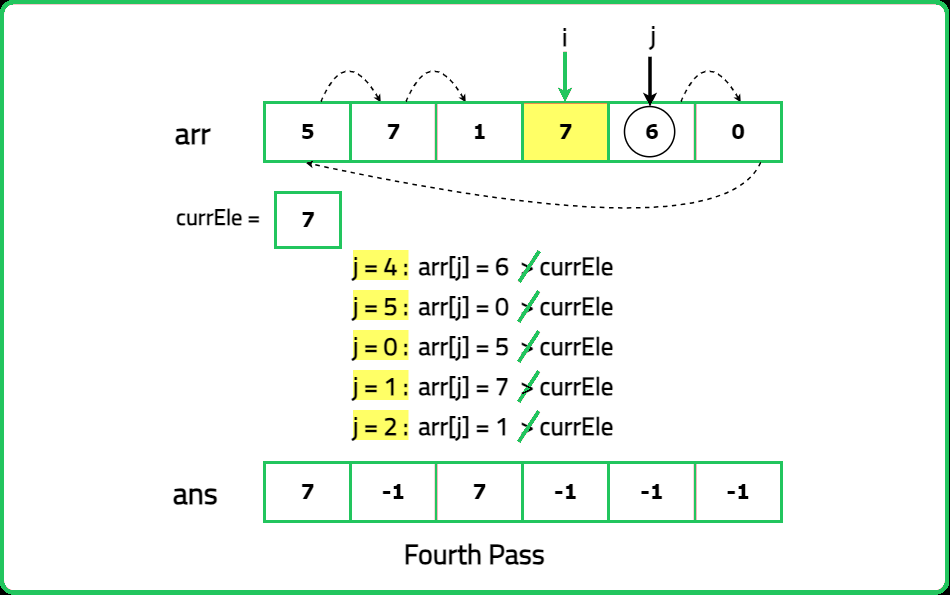
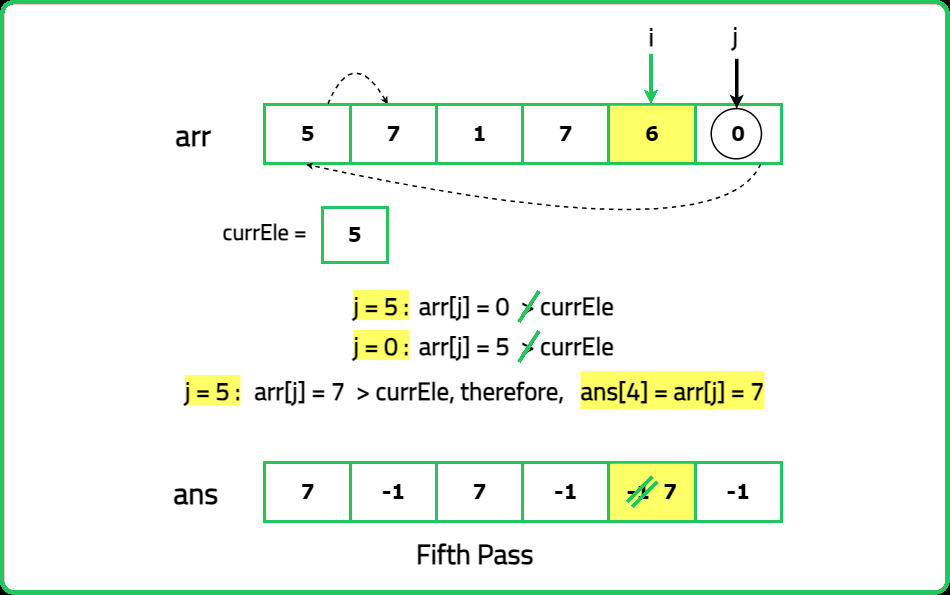
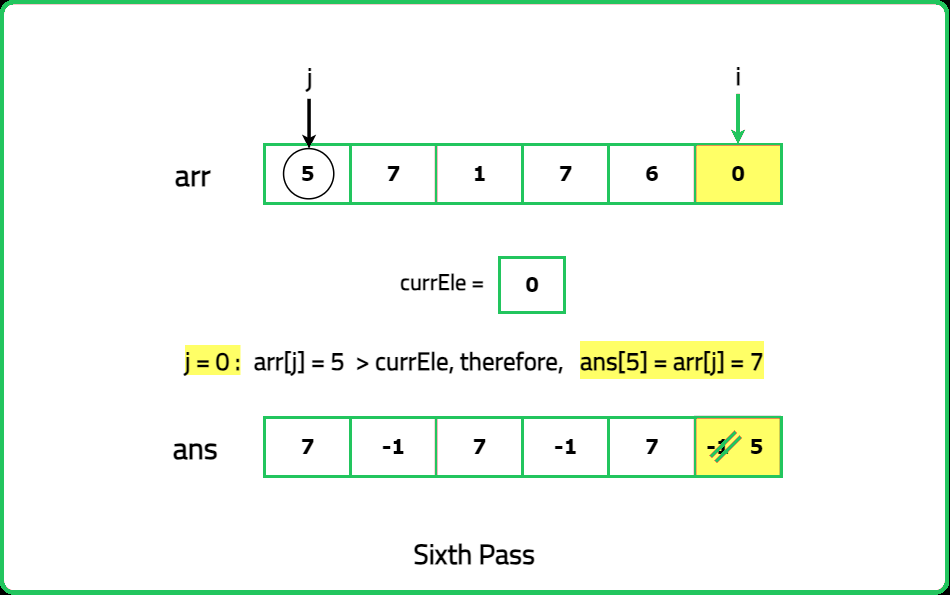
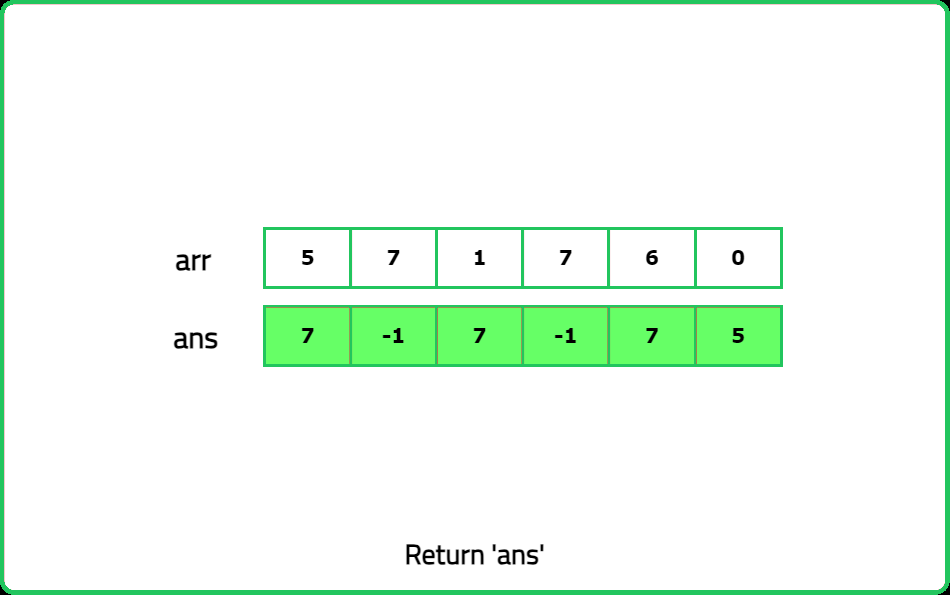
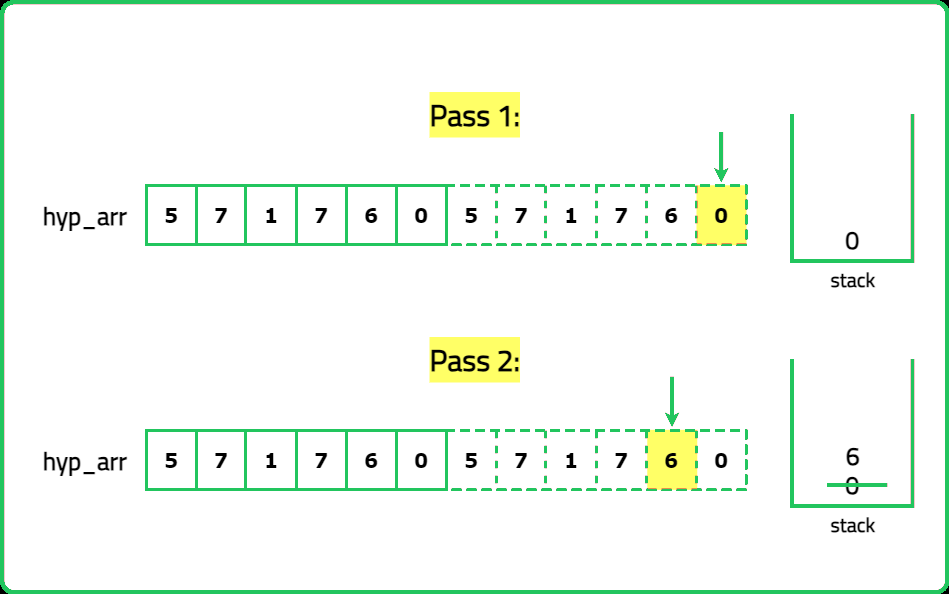
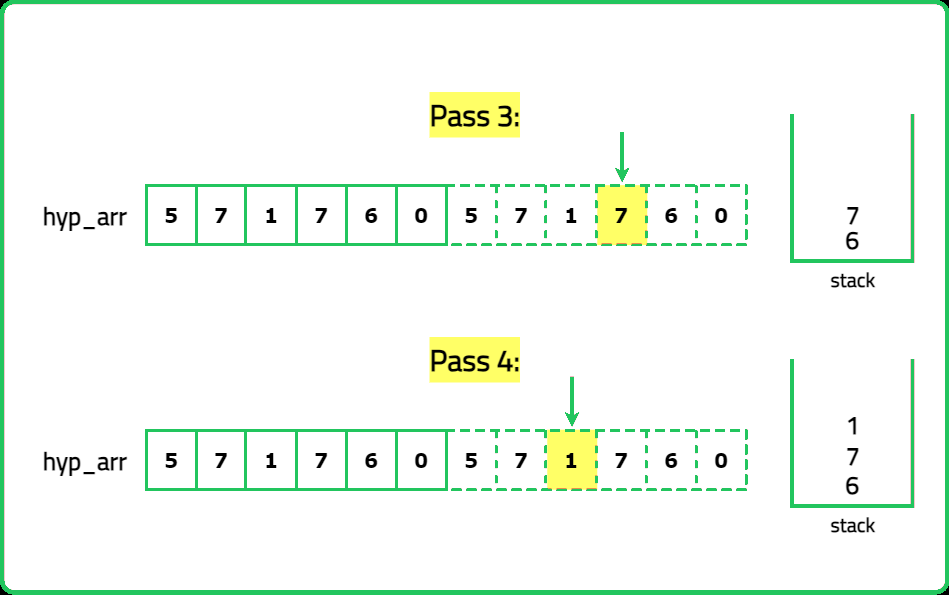
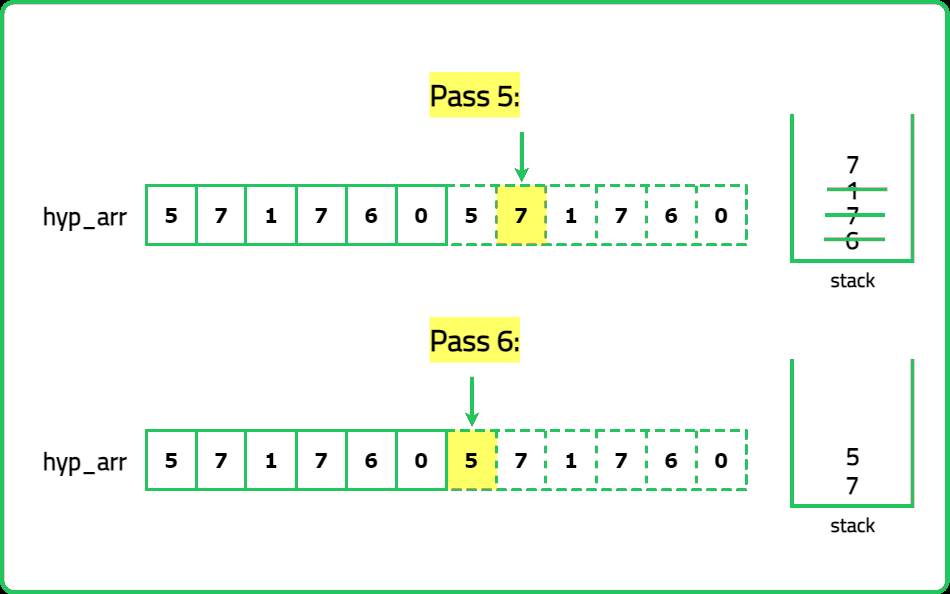
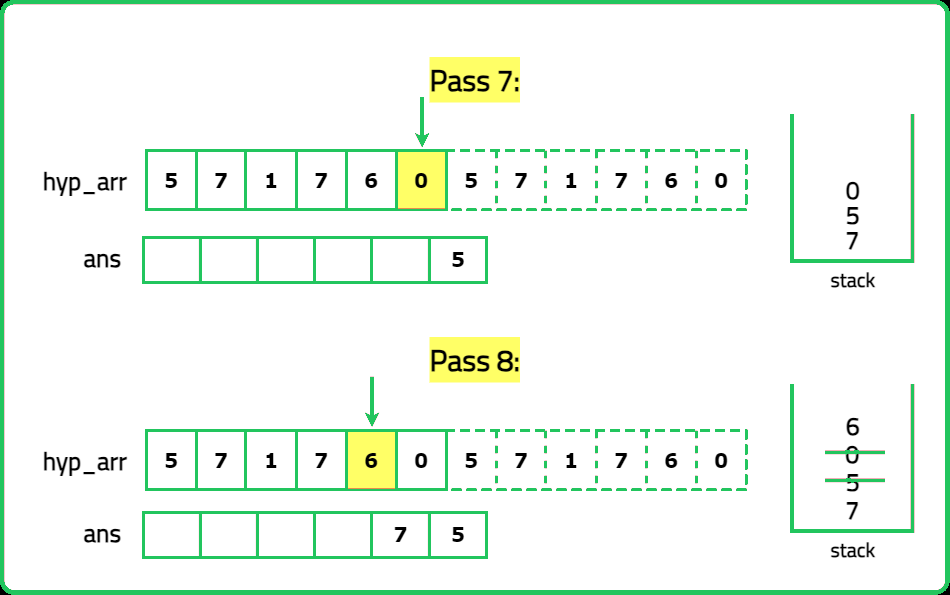
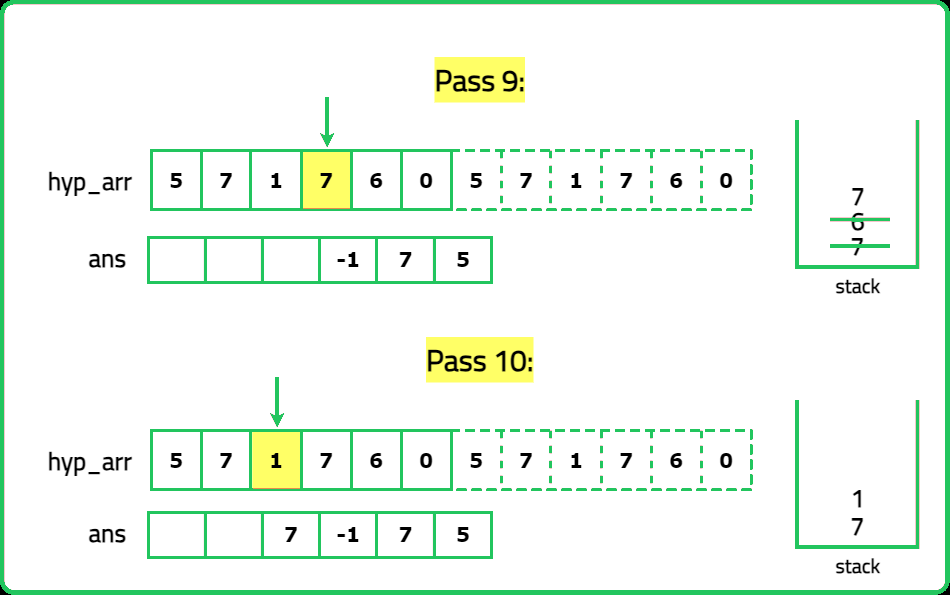
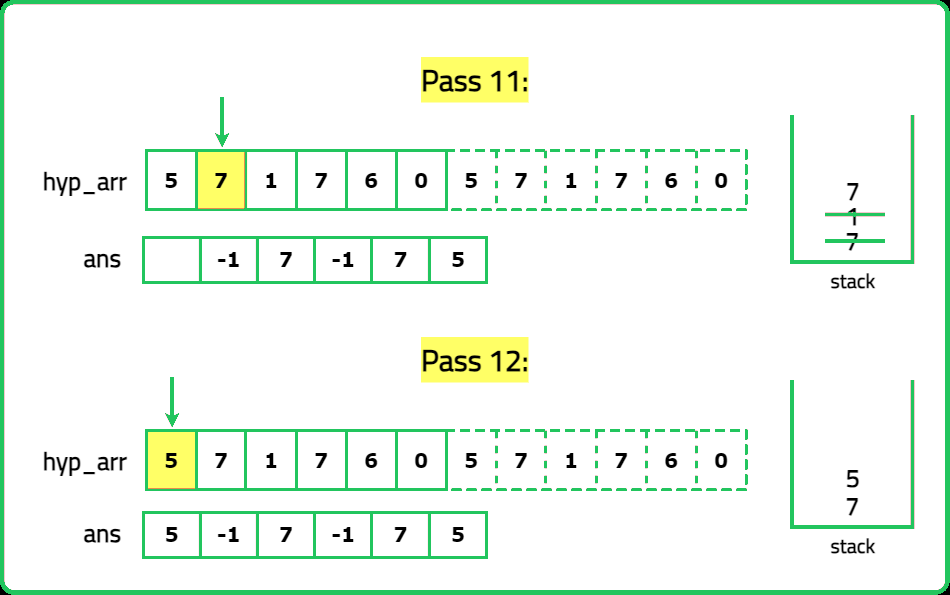
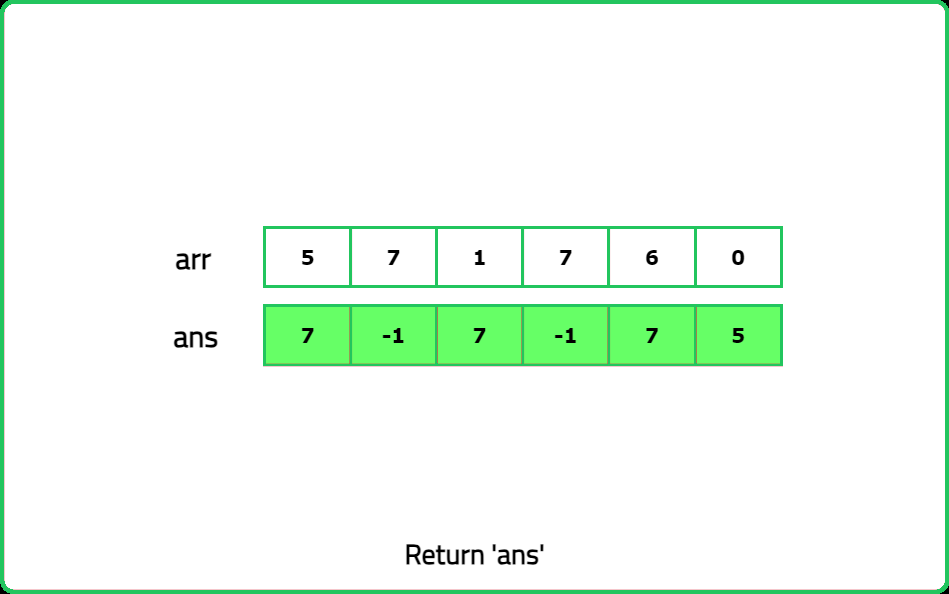
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the next greater
element for each element in the array */
vector<int> nextGreaterElements(vector<int> arr) {
int n = arr.size(); //size of array
// To store the next greater elements
vector<int> ans(n);
// Stack to get elements in LIF fashion
stack<int> st;
// Start traversing from the back
for(int i = 2*n-1; i >= 0; i--) {
// Get the actual index
int ind = i % n;
// Get the current element
int currEle = arr[ind];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while(!st.empty() && st.top() <= currEle) {
st.pop();
}
// Store the answer for the second half
if(i < n) {
/* If the greater element is not
found, stack will be empty */
if(st.empty())
ans[i] = -1;
// Else store the answer
else
ans[i] = st.top();
}
/* Push the current element in the stack
maintaining the decreasing order */
st.push(currEle);
}
// Return the result
return ans;
}
};
int main() {
int n = 6;
vector<int> arr = {5, 7, 1, 7, 6, 0};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the next greater
element for each element in the array */
vector<int> ans = sol.nextGreaterElements(arr);
cout << "The next greater elements are: ";
for(int i=0; i < n; i++) {
cout << ans[i] << " ";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
import java.util.*;
class Solution {
/* Function to find the next greater
element for each element in the array */
public int[] nextGreaterElements(int[] arr) {
int n = arr.length; // size of array
// To store the next greater elements
int[] ans = new int[n];
// Stack to get elements in LIFO fashion
Stack<Integer> st = new Stack<>();
// Start traversing from the back
for (int i = 2 * n - 1; i >= 0; i--) {
// Get the actual index
int ind = i % n;
// Get the current element
int currEle = arr[ind];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while (!st.isEmpty() && st.peek() <= currEle) {
st.pop();
}
// Store the answer for the second half
if (i < n) {
/* If the greater element is not
found, stack will be empty */
if (st.isEmpty())
ans[i] = -1;
// Else store the answer
else
ans[i] = st.peek();
}
/* Push the current element in the stack
maintaining the decreasing order */
st.push(currEle);
}
// Return the result
return ans;
}
public static void main(String[] args) {
int n = 6;
int[] arr = {5, 7, 1, 7, 6, 0};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the next greater
element for each element in the array */
int[] ans = sol.nextGreaterElements(arr);
System.out.print("The next greater elements are: ");
for (int i = 0; i < n; i++) {
System.out.print(ans[i] + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
class Solution:
# Function to find the next greater
# element for each element in the array
def nextGreaterElements(self, arr):
n = len(arr) # size of array
# To store the next greater elements
ans = [-1] * n
# Stack to get elements in LIFO fashion
st = []
# Start traversing from the back
for i in range(2 * n - 1, -1, -1):
# Get the actual index
ind = i % n
# Get the current element
currEle = arr[ind]
# Pop the elements in the stack until
# the stack is not empty and the top
# element is not the greater element
while st and st[-1] <= currEle:
st.pop()
# Store the answer for the second half
if i < n:
# If the greater element is not
# found, stack will be empty
if st:
ans[i] = st[-1]
# Push the current element in the stack
# maintaining the decreasing order
st.append(currEle)
# Return the result
return ans
# Driver Code
if __name__ == "__main__":
arr = [5, 7, 1, 7, 6, 0]
# Creating an instance of Solution class
sol = Solution()
# Function call to find the next greater
# element for each element in the array
ans = sol.nextGreaterElements(arr)
print("The next greater elements are:", ans)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
class Solution {
/* Function to find the next greater
element for each element in the array */
nextGreaterElements(arr) {
let n = arr.length; // size of array
// To store the next greater elements
let ans = new Array(n).fill(-1);
// Stack to get elements in LIFO fashion
let st = [];
// Start traversing from the back
for (let i = 2 * n - 1; i >= 0; i--) {
// Get the actual index
let ind = i % n;
// Get the current element
let currEle = arr[ind];
/* Pop the elements in the stack until
the stack is not empty and the top
element is not the greater element */
while (st.length > 0 && st[st.length - 1] <= currEle) {
st.pop();
}
// Store the answer for the second half
if (i < n) {
/* If the greater element is not
found, stack will be empty */
if (st.length > 0)
ans[i] = st[st.length - 1];
}
/* Push the current element in the stack
maintaining the decreasing order */
st.push(currEle);
}
// Return the result
return ans;
}
}
// Driver Code
let arr = [5, 7, 1, 7, 6, 0];
// Creating an instance of Solution class
let sol = new Solution();
// Function call to find the next greater
// element for each element in the array
let ans = sol.nextGreaterElements(arr);
console.log("The next greater elements are:", ans);