Search in a 2D matrix

Binary Search 2D Arrays Hard

This problem is essentially a form of sorted matrix search, a concept widely applied in database querying systems and search engines
When handling large volumes of data arranged in a sorted format (like timestamps/logs), efficient searching algorithms are critical for performance
Applications like Google, where millions of search queries are performed each second, need to effectively implement algorithms similar to this problem in their infrastructure
These systems frequently use multi-dimensional arrays (matrices) for quicker access and traversal, hence the significance of such problems

Given a 2-D array mat where the elements of each row are sorted in non-decreasing order, and the first element of a row is greater than the last element of the previous row (if it exists), and an integer target, determine if the target exists in the given mat or not.

Examples:

Input: mat = [ [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12] ], target = 8

Output: True

Explanation: The target = 8 exists in the 'mat' at index (1, 3).

Input: mat = [ [1, 2, 4], [6, 7, 8], [9, 10, 34] ], target = 78

Output: False

Explanation: The target = 78 does not exist in the 'mat'. Therefore in the output, we see 'false'.

Input: mat = [ [1, 2, 4], [6, 7, 8], [9, 10, 34] ], target = 7

Constraints

n == mat.length
m == mat[i].length
1 <= m, n <= 100
-10⁴ <= mat[i][j], target <= 10⁴

Hints

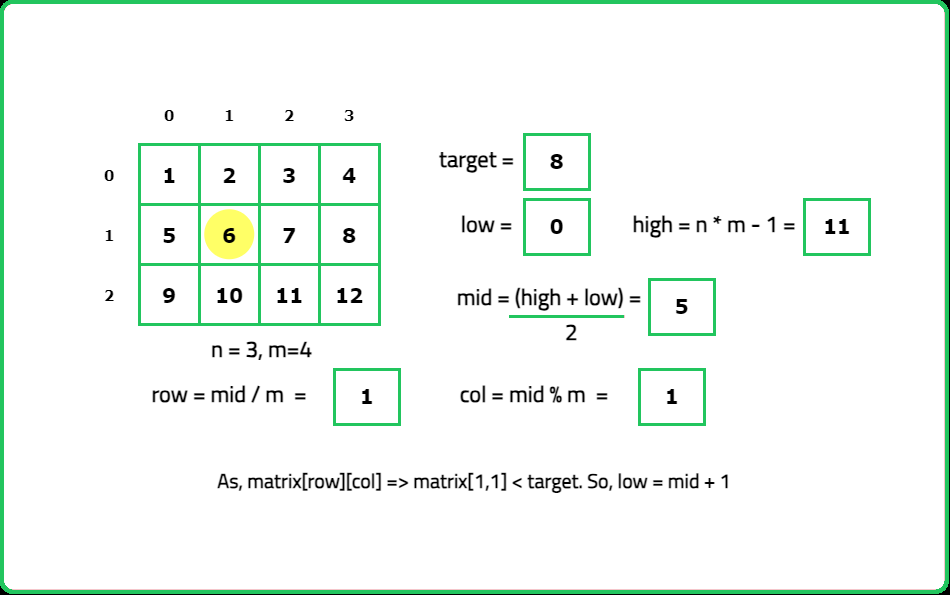
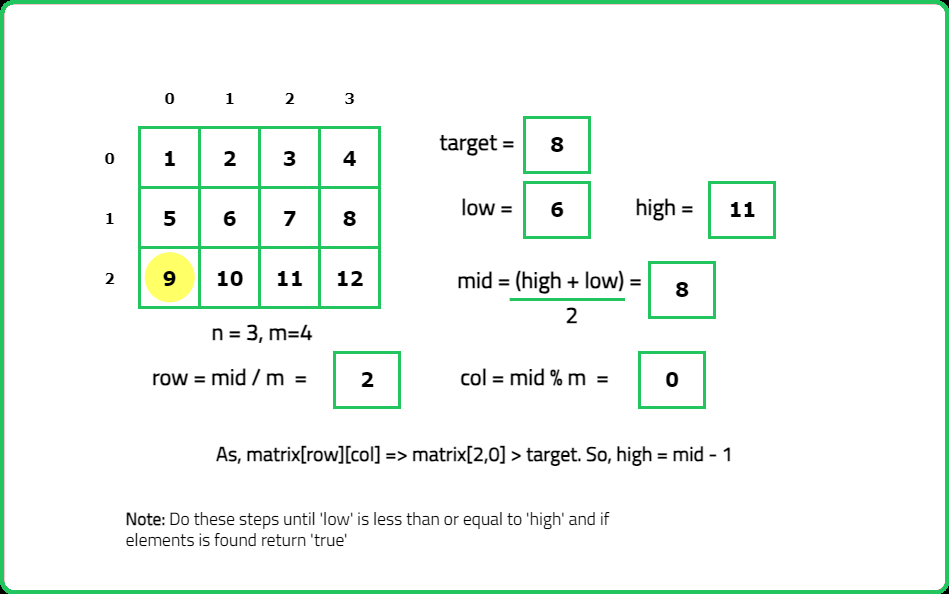
Treat the matrix as a 1D array with indices ranging from 0 to m×n−1, where m is the number of rows and n is the number of columns.
Map the 1D index mid to a 2D position using: row=mid/n, col=mid%n

Company Tags

Pinterest Square Docker Airbnb Bloomberg Ernst & Young Robinhood Epic Games Mastercard IBM American Express McKinsey & Company Dropbox HCL Technologies Lyft Chewy Intel PayPal Medtronic Seagate Technology Ubisoft Freshworks ARM Flipkart Siemens Healthineers Google Microsoft Amazon Meta Apple Netflix Adobe

Intuition:

The extremely naive approach is to get the answer by checking all the elements of the given matrix. So, traverse each cell of the matrix and check every element, if it is equal to the given ‘target’.

Approach:

First, traverse each row of the matrix by using a for loop.
Next, for each row, initialize another for loop which will basically traverse all the columns.
Inside the nested loops, check if the element at current cell is equal to the ‘target’. If yes, return true as the target element is found. Otherwise, after completing the traversal, return false as it means no matching element is found in the matrix.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to search for a given target in matrix
    bool searchMatrix(vector<vector<int>>& mat, int target) {
        // Check if the matrix is empty
        if (mat.empty() || mat[0].empty()) {
            return false;
        }
        
        int n = mat.size();    
        int m = mat[0].size(); 
        
        // Traverse the matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (mat[i][j] == target) {
                    // Return true if target is found
                    return true; 
                }
            }
        }
        
        // Return false if target is not found
        return false; 
    }
};

int main() {
    
    vector<vector<int>> matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
    int target = 8;
    
    //Create an instace of Solution class
    Solution sol;
    
    bool result = sol.searchMatrix(matrix, target);
    
    // Output the result
    result ? cout << "true\n" : cout << "false\n";
    
    return 0;
}
import java.util.*;

class Solution {
    //Function to search for a given target in matrix
    public boolean searchMatrix(int[][] mat, int target) {
        // Check if the matrix is empty
        if (mat.length == 0 || mat[0].length == 0) {
            return false;
        }
        
        int n = mat.length;  
        int m = mat[0].length; 
        
        // Traverse the matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (mat[i][j] == target) {
                    // Return true if target is found
                    return true; 
                }
            }
        }
        // Return false if target is not found
        return false; 
    }
    
    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
        int target = 8;
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        boolean result = sol.searchMatrix(matrix, target);
        
        // Output the result
        System.out.println(result ? "true" : "false");
    }
}
class Solution:
    
    def searchMatrix(self, mat, target):
        # Check if the matrix is empty
        if not mat or not mat[0]:
            return False
        
        n = len(mat)     
        m = len(mat[0])  
        
        # Traverse the matrix
        for i in range(n):
            for j in range(m):
                if mat[i][j] == target:
                    # Return true if target is found
                    return True  
        
        # Return false if target is not found
        return False 

if __name__ == "__main__":
    matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
    target = 8
    
    # Create an instance of Solution class
    sol = Solution()
    
    result = sol.searchMatrix(matrix, target)
    
    # Output the result
    print("true" if result else "false")
class Solution {
    
    searchMatrix(mat, target) {
        // Check if the matrix is empty
        if (mat.length === 0 || mat[0].length === 0) {
            return false;
        }
        
        let n = mat.length;    
        let m = mat[0].length; 
        
        // Traverse the matrix
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < m; j++) {
                if (mat[i][j] === target) {
                    
                    // Return true if target is found
                    return true;
                }
            }
        }
        // Return false if target is not found
        return false; 
    }
}

let matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]];
let target = 8;

// Create an instance of Solution class
let sol = new Solution();

let result = sol.searchMatrix(matrix, target);

// Output the result
console.log(result ? "true" : "false");

Complexity Analysis:

Time Complexity: O(N X M), where N is the number of rows in the matrix, M is the number of columns in each row. As, nested loops are being used to traverse the matrix.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Intuition:

As each row of the given matrix is sorted, it means the first element of each row will be less than or equal to the last element of each row. Therefore, for each row, check if the target belongs to that particular row. This can be done by verifying if the target lies between the first and the last element of the row. Once the row in which the target might lie has been identified, use the binary search algorithm on that row to check if the target is actually present. If it is, return true; otherwise, return false.

Approach:

Working of searchMatrix(matrix, target):

First, traverse each row of the matrix using a for loop.
Next, for every row, check if it contains the target. If the target is greater than or equal to the first element of the row and the target is less than or equal to the last element of the row, it can be concluded that the present row has the possibility of containing the target.
If the present row has the possibility to contain the target, apply binary search on the row and check if the target is actually present. If it is, return true from this step. Otherwise, return false.
Also, after completing the traversal, return false to conclude that target is not found.

Working of binarySearch(arr, target):

First initialize low to 0 and and high to the last column index. This will define the search range of the binary search.
While low is less than or equal to high, calculate 'mid' and check if the element at mid is equal to target, if so, return true. Otherwise, if element at mid is greater than target, eliminate the right half, else eliminate the left half.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Fuction to perform binary search 
    bool binarySearch(vector<int>& mat, int target) {
        int n = mat.size(); 
        int low = 0, high = n - 1;

        //Perform binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            
            //Return true if target is found
            if (mat[mid] == target) return true;
            else if (target > mat[mid]) low = mid + 1;
            else high = mid - 1;
        }
        //Return false if target not found
        return false;
    }
public:
    //Function to search for a given target in matrix
    bool searchMatrix(vector<vector<int>>& mat, int target) {
        int n = mat.size();
        int m = mat[0].size();

        for (int i = 0; i < n; i++) {
            
            /*Check if there is a possibility that
            the target can be found in current row*/
            if (mat[i][0] <= target && target <= mat[i][m - 1]) {
                
                /*Return result fetched 
                from helper function*/
                return binarySearch(mat[i], target);
            }
        }
        // Return false if target is not found
        return false; 
    }
};

int main() {
    
    vector<vector<int>> matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
    int target = 8;
    
    //Create an instace of Solution class
    Solution sol;
    
    bool result = sol.searchMatrix(matrix, target);
    
    // Output the result
    result ? cout << "true\n" : cout << "false\n";
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to perform binary search
    private boolean binarySearch(int[] nums, int target) {
        int n = nums.length; 
        int low = 0, high = n - 1;

        // Perform binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            
            // Return true if target is found
            if (nums[mid] == target) return true;
            else if (target > nums[mid]) low = mid + 1;
            else high = mid - 1;
        }
        // Return false if target not found
        return false;
    }
    
    // Function to search for a given target in matrix
    public boolean searchMatrix(int[][] mat, int target) {
        int n = mat.length;
        int m = mat[0].length;

        for (int i = 0; i < n; i++) {
            
            /* Check if there is a possibility that 
            the target can be found in current row*/
            if (mat[i][0] <= target && target <= mat[i][m - 1]) {
                
                /* Return result fetched 
                from helper function*/
                return binarySearch(mat[i], target);
            }
        }
        // Return false if target is not found
        return false; 
    }
    
    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
        int target = 8;
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        boolean result = sol.searchMatrix(matrix, target);
        
        // Output the result
        System.out.println(result ? "true" : "false");
    }
}
class Solution:
    
    # Function to perform binary search
    def binarySearch(self, nums, target):
        n = len(nums)
        low, high = 0, n - 1

        # Perform binary search
        while low <= high:
            mid = (low + high) // 2
            
            # Return true if target is found
            if nums[mid] == target:
                return True
            elif target > nums[mid]:
                low = mid + 1
            else:
                high = mid - 1
        
        # Return false if target not found
        return False
    
    # Function to search for a given target in matrix
    def searchMatrix(self, mat, target):
        n = len(mat)
        m = len(mat[0])

        for i in range(n):
            
            """ Check if there is a possibility that 
            the target can be found in current row"""
            if mat[i][0] <= target <= mat[i][m - 1]:
                
                """ Return result fetched 
                from helper function"""
                return self.binarySearch(mat[i], target)
        
        # Return false if target is not found
        return False

if __name__ == "__main__":
    matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
    target = 8
    
    # Create an instance of Solution class
    sol = Solution()
    
    result = sol.searchMatrix(matrix, target)
    
    # Output the result
    print("true" if result else "false")
class Solution {
    // Function to perform binary search
    binarySearch(nums, target) {
        let n = nums.length;
        let low = 0, high = n - 1;

        // Perform binary search
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
            
            // Return true if target is found
            if (nums[mid] === target) return true;
            else if (target > nums[mid]) low = mid + 1;
            else high = mid - 1;
        }
        // Return false if target not found
        return false;
    }
    
    // Function to search for a given target in matrix
    searchMatrix(mat, target) {
        let n = mat.length;
        let m = mat[0].length;

        for (let i = 0; i < n; i++) {
            
            /* Check if there is a possibility that 
            the target can be found in current row*/
            if (mat[i][0] <= target && target <= mat[i][m - 1]) {
                
                /* Return result fetched 
                from helper function*/
                return this.binarySearch(mat[i], target);
            }
        }
        // Return false if target is not found
        return false; 
    }
}

let matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]];
let target = 8;

// Create an instance of Solution class
let sol = new Solution();

let result = sol.searchMatrix(matrix, target);

// Output the result
console.log(result ? "true" : "false");

Complexity Analysis:

Time Complexity: O(N + logM), where N is given row number, M is given column number. The rows are traversed in O(N) time complexity. Binary search is applied only once for a particular row, resulting in a time complexity of O(N + logM) instead of O(N*logM).

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Intuition:

The idea here is to flattent he 2-D matrix into 1-D matrix and then apply the binary seacrh algorithm on it. The resultant 1-D matrix will be of length N*M. If the 2D matrix is flattened, it will require O(N x M) time complexity and extra space to store the 1D array. In that case, the optimal solution will no longer be maintained. So, it is needed to flatten the matrix without actually doing it.

How to apply binary search on the 1D array without actually flattening the 2D matrix:

If the index of the 1D array can be converted into the corresponding cell number in the 2D matrix, our task will be completed. In this scenario, binary search will be used with the indices of the imaginary 1D array, ranging from 0 to (NxM)-1 (total number of elements in the 1D array = NxM). When elements are compared, the index will be converted to the cell number, and the element will be retrieved. Thus, binary search can be applied in the imaginary 1D array.
If index = i, and no. of columns in the matrix = m, the index i corresponds to the cell with row = i / m and col = i % m. More formally, the cell is (i / m, i % m)(0-based indexing).

Approach:

Initialize 2 pointers i.e. low and high. The pointer low will point to 0 and the high will point to (NxM)-1, where N is total row and M is total column per row. It will basically define the search range.
Now, intialize a while loop which will run till low is less than or equal to high. Calculate the value of ‘mid’ using the following formula: mid = (low+high) // 2 ( ‘//’ refers to integer division)
To get the element, convert index ‘mid’ to the corresponding cell using the formula mentioned earlier. Here number of columns of the matrix is M. row = mid / M, col = mid % M.
If element at cell (row,col) is equal to target, return true, as ‘target’ has been found.
If element at cell (row,col) is less than target, in this case, a bigger element is needed. So, eliminate the left half and consider the right half (low = mid+1).
If element at cell (row,col) is greater than the target, it suggests a smaller element is needed. So, eliminate the right half and consider the left half (high = mid-1).
Do these steps until low crosses high, after the loop terminates return false as, target is not found.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to search for a given target in matrix
    bool searchMatrix(vector<vector<int>>& mat, int target) {
        int n = mat.size();
        int m = mat[0].size();

        int low = 0, high = n * m - 1;
        //Perform binary search
        while (low <= high) {
            int mid = (low + high) / 2;
                
            //Calculate the row and column
            int row = mid / m, col = mid % m;
                
            //If target is found return true
            if (mat[row][col] == target) return true;
            else if (mat[row][col] < target) low = mid + 1;
            else high = mid - 1;
        }
        // Return false if target is not found
        return false; 
    }
};

int main() {
    
    vector<vector<int>> matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
    int target = 8;
    
    //Create an instace of Solution class
    Solution sol;
    
    bool result = sol.searchMatrix(matrix, target);
    
    // Output the result
    result ? cout << "true\n" : cout << "false\n";
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to search for a given target in matrix
    public boolean searchMatrix(int[][] mat, int target) {
        int n = mat.length;
        int m = mat[0].length;

        int low = 0, high = n * m - 1;
        
        // Perform binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            
            // Calculate the row and column
            int row = mid / m;
            int col = mid % m;
            
            // If target is found return true
            if (mat[row][col] == target) return true;
            else if (mat[row][col] < target) low = mid + 1;
            else high = mid - 1;
        }
        
        // Return false if target is not found
        return false; 
    }
    
    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
        int target = 8;
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        boolean result = sol.searchMatrix(matrix, target);
        
        // Output the result
        System.out.println(result ? "true" : "false");
    }
}
class Solution:
    # Function to search for a given target in matrix
    def searchMatrix(self, mat, target):
        n = len(mat)
        m = len(mat[0])

        low, high = 0, n * m - 1
        
        # Perform binary search
        while low <= high:
            mid = (low + high) // 2
            
            # Calculate the row and column
            row = mid // m
            col = mid % m
            
            # If target is found return true
            if mat[row][col] == target:
                return True
            elif mat[row][col] < target:
                low = mid + 1
            else:
                high = mid - 1
        
        # Return false if target is not found
        return False

if __name__ == "__main__":
    matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
    target = 8
    
    # Create an instance of Solution class
    sol = Solution()
    
    result = sol.searchMatrix(matrix, target)
    
    # Output the result
    print("true" if result else "false")
class Solution {
    // Function to search for a given target in matrix
    searchMatrix(mat, target) {
        let n = mat.length;
        let m = mat[0].length;

        let low = 0, high = n * m - 1;
        
        // Perform binary search
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
            
            // Calculate the row and column
            let row = Math.floor(mid / m);
            let col = mid % m;
            
            // If target is found return true
            if (mat[row][col] === target) return true;
            else if (mat[row][col] < target) low = mid + 1;
            else high = mid - 1;
        }
        
        // Return false if target is not found
        return false; 
    }
}

let matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]];
let target = 8;

// Create an instance of Solution class
let sol = new Solution();

let result = sol.searchMatrix(matrix, target);

// Output the result
console.log(result ? "true" : "false");

Complexity Analysis:

Time Complexity: O(log(N*M)), where N is the number of rows in the matrix, M is the number of columns in each row. As, binary search is being applied on the 1-D array of size N*M.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Code

Problem List

Search in a 2D matrix

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code