Selection Sort
Sorting
Algorithms
Easy
- Fun Fact: The Selection Sort algorithm, which is the focus of this problem, is widely used in software development for its simplicity and efficiency when dealing with small data sets
- It serves as a building block in various applications like e-commerce platforms and database technologies, where sorting of data is an important functionality
- In real-world applications, it would often be used as a part of a more complex sorting algorithm to sort small sublists within a larger, more complex, sorting problem
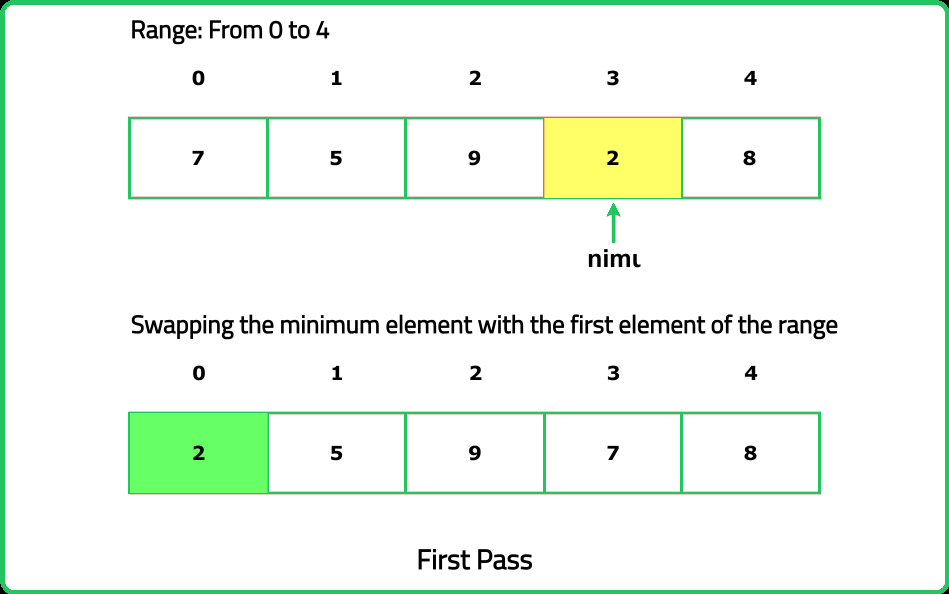
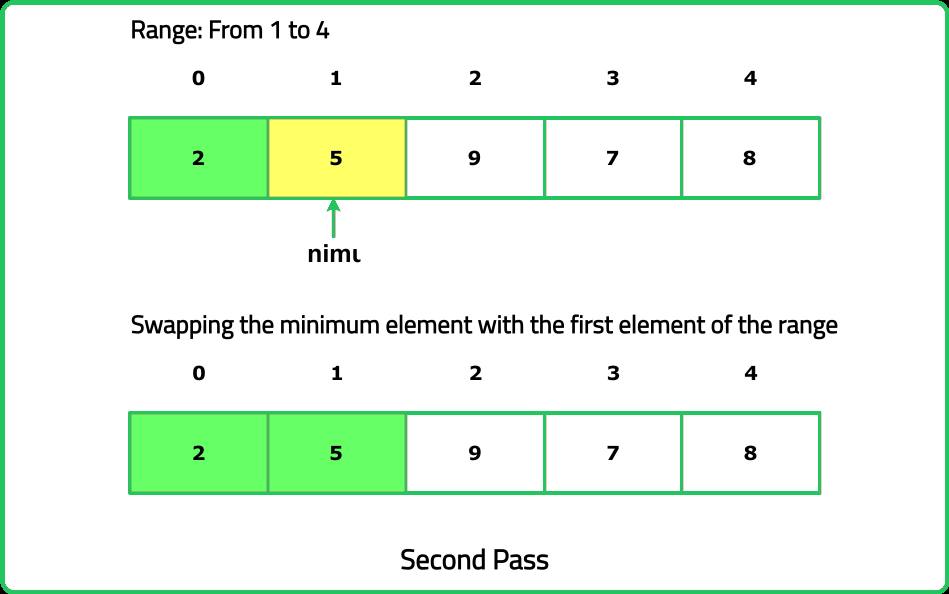
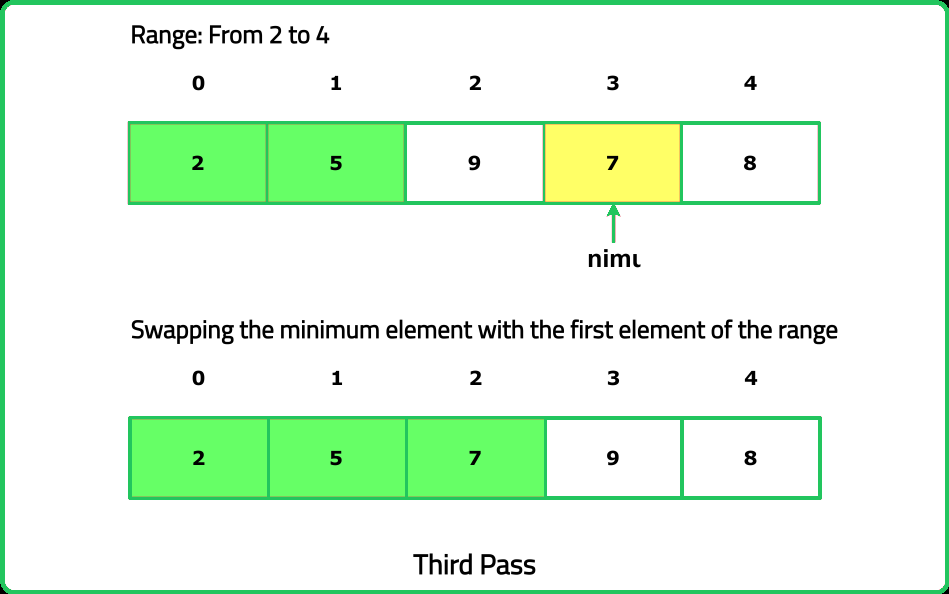
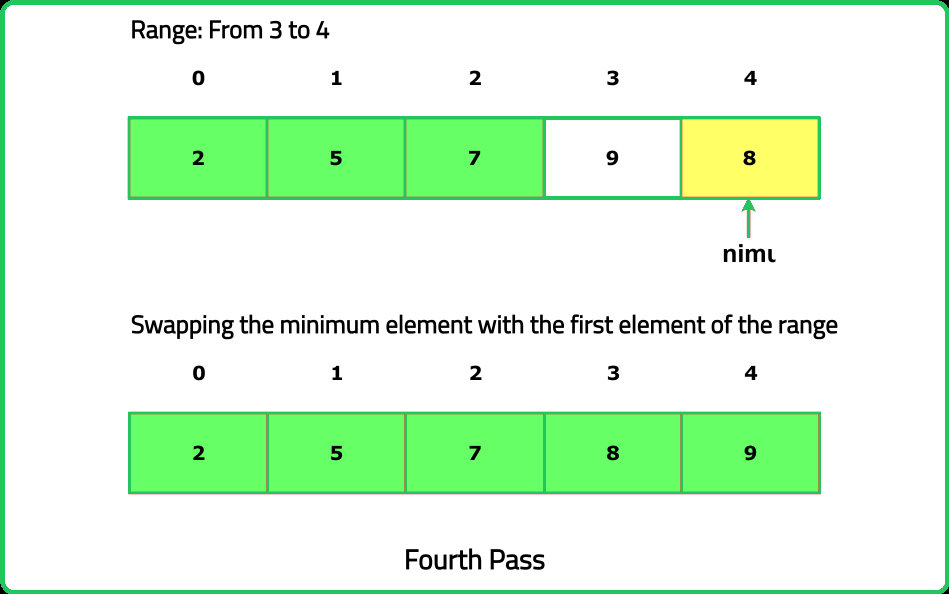
Given an array of integers nums, sort the array in non-decreasing order using the selection sort algorithm and return the sorted array.
A sorted array in non-decreasing order is an array where each element is greater than or equal to all previous elements in the array.
Examples:
Input: nums = [7, 4, 1, 5, 3]
Output: [1, 3, 4, 5, 7]
Explanation: 1 <= 3 <= 4 <= 5 <= 7.
Thus the array is sorted in non-decreasing order.
Input: nums = [5, 4, 4, 1, 1]
Output: [1, 1, 4, 4, 5]
Explanation: 1 <= 1 <= 4 <= 4 <= 5.
Thus the array is sorted in non-decreasing order.
Input: nums = [3, 2, 3, 4, 5]
Constraints
- 1 <= nums.length <= 1000
- -104 <= nums[i] <= 104
- nums[i] may contain duplicate values.
Hints
- Think Small First, at each step, identify the smallest element in the unsorted portion of the array and place it in its correct position.
- Use Divide and Conquer Mindset, visualize sorting as splitting the array into sorted and unsorted parts, and shrinking the unsorted part one element at a time.
- Focus on how you can repeatedly compare elements and rearrange them in-place without needing additional memory.
Company Tags
Bungie
Qualcomm
Uber
Morgan Stanley
Zoho
Electronic Arts
Reddit
Ubisoft
PwC
Broadcom
Rakuten
OYO Rooms
Seagate Technology
Epic Games
Nutanix
Target
Pinterest
Boston Consulting Group
Optum
KPMG
JPMorgan Chase
Cerner
MongoDB
Red Hat
McKinsey & Company
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro